脑网络中的高阶拓扑结构

导语
人脑是一个复杂系统,追寻更精准的控制与协调、更清晰的感知、面对生存危机或机遇的快速的决策能力等等。针对脑网络分析发现,在脑部宏观计算和认知时,会受到一系列错综复杂的神经物理机制的影响。将大脑区域及其连接编码为节点和边的网络,研究分析在人类处理和执行复杂行为时,网络拓扑特性的呈现和变化,体现了脑网络中的信息交互和功能反应机制。
今天介绍一篇2018年发表在Journal of computational neuroscience上的高引用文章“人类连接体中的团和洞”(Cliques and cavities in the human connectome),作者利用代数拓扑学的技术为结构连接学提供了一个新的视角,探讨脑网络中的高阶拓扑结构,可以提供对大脑功能复杂性的基本见解。
为了探索高阶交互结构,聚焦网络科学前沿,集智俱乐部发起了「高阶网络读书会」,研读分享相关研究。读书会自6月28日起,持续10-12周,并特邀Ginestra Bianconi等一线学者做报告。欢迎从事复杂网络研究与应用的朋友加入。详情见文末。
研究领域:拓扑应用,复杂网络,高阶拓扑,脑网络,网络神经学

高爽 | 作者
邓一雪 | 编辑

论文题目:
Sizemore, Ann E., Chad Giusti, Ari Kahn, Jean M. Vettel, Richard F. Betzel, and Danielle S. Bassett. “Cliques and cavities in the human connectome.” Journal of computational neuroscience 44, no. 1 (2018): 115-145.
论文链接:
https://link.springer.com/content/pdf/10.1007/s10827-017-0672-6.pdf
前言
前言
脑网络中的节点体现了解剖上定义的大脑区域,这些区域通过白质束网络不断在彼此之间共享信息,从而构建为脑结构拓扑网络。在以往的研究课题中,主要是找寻由大片区域成对紧密相连的区域集合,称为社区(communities)、模块(modules )以及富人俱乐部( rich clubs)。因此在分析结构网络时,关注局部强连接区域成为大势所趋。然而从更宏观的角度来看脑网络,其中较小或者缺失的白质束直观地起到了隔离强白质束过程的作用。换句话说,弱连接或缺失边,为强连接区域起到了“划分”作用。
在本文中,作者为了理解大脑中强连接和弱连接之间的相互作用,从只考虑成对相互作用转向捕捉更高阶的关系,用团(cliques),即网络中的全连接子图,代表强相互连接的计算单元。团的数量和大小使人们对整个大脑的局部连接强度有一个总体的认识。并通过研究团形成的环来分析在中尺度脑网络中的结构特征。这些团和环对应于潜在信息传输的扩展路径,沿着这些路径可以连续进行计算,以发散或收敛的方式实现认知(即信息的分布或整合),文中将这些 “封闭的空间 “称为网络中的拓扑洞(topological cavities)。作者假设,团和洞的空间分布将在其解剖位置上有所不同,与它们在神经计算中的不同作用相对应。将团和洞两个视角相结合,提供了一个更完整的网络功能视图。
1. 脑网络中的团
1. 脑网络中的团
在文章中,为了提取人脑结构连接体的相关结构特征,从8名健康成年人获得的扩散光谱成像(diffusion spectrum imaging, DSI)数据编码为无向加权网络。在这个网络中,节点对应于83个大脑区域,边缘对应于节点对之间的白质束密度,并使用边缘密度(ρ)为0.25时的组平均网络阈值来去除虚假边。为进行统计验证构建空模型,将24次扫描的大脑区域,根据最短路径连接,边缘权重为欧几里得距离的倒数。这个模型模仿了大脑中的倾向连接方式来节省布线成本,即物理连接上接近的节点之间连边具有更高的权重。
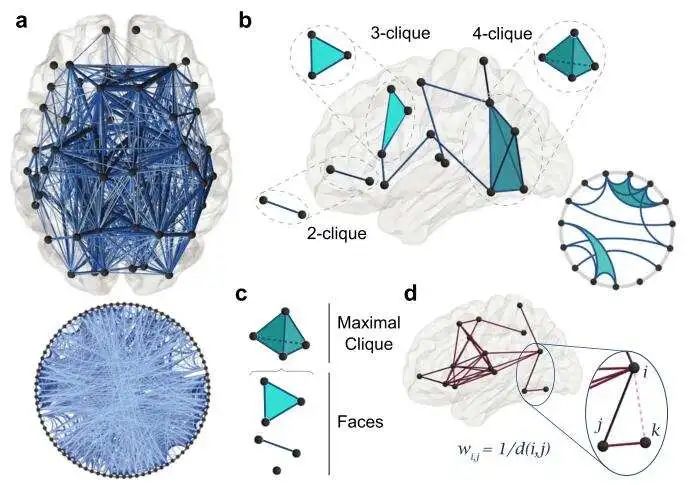
团是结构性脑网络中的局部区域特征。拓扑分析的第一步是对平均结构网络中的所有最大k-团进行计数。k-团是具有所有成对连接的k个节点的集合 (2-团、3-团和4-团分别表示边、三角形和四面体) 。根据定义,一个团的子图本身就是一个较低维度的团,称为面。最大团是指不是任何其他团的面的团。
为了了解真实模型网络和空模型网络中最大团的解剖分布,定义一个节点作为成员参与最大k-团的数量,称为节点参与度。
作者通过统计不同阶的团,观察到最大团的度分布在最小连接空模型中是单峰的,在经验数据中是定性的双峰分布 (见图2a)。在解剖学上,随着检测程度增高,最大团参与度从皮层的前部到后部普遍存在 (图2a)。在真实情况下,由12-16个节点组成的最大团几乎包含了所有的视觉皮质。这种空间分布表明,早期信息处理需要大量相互作用的脑区,而驱动高级认知的额叶皮质区域则利用较小的工作簇完成。结果还显示了,人脑显示出对小 (4-6个节点) 和大 (12-16个节点) 处理单元的偏好,而不是像最小连线空模型中那样的中等大小 (大约8个节点) 单元。
最大团的前后梯度可以通过额外分析正在执行的认知计算中的区域差异来补充。具体地说,讨论最大团中的节点参与在特定的认知系统中是否存在不同。统计不同区域的团,最大团是由(几乎完全位于)皮质下、背侧注意、视觉和默认模式系统的节点形成的,这表明这些系统紧密地相互联系,可能利用鲁棒的局部拓扑进行通信。这些数据表明,较小的团作为局部处理系统可能是整个系统的常见特征,而较大的团可能允许快速的多系统串扰。
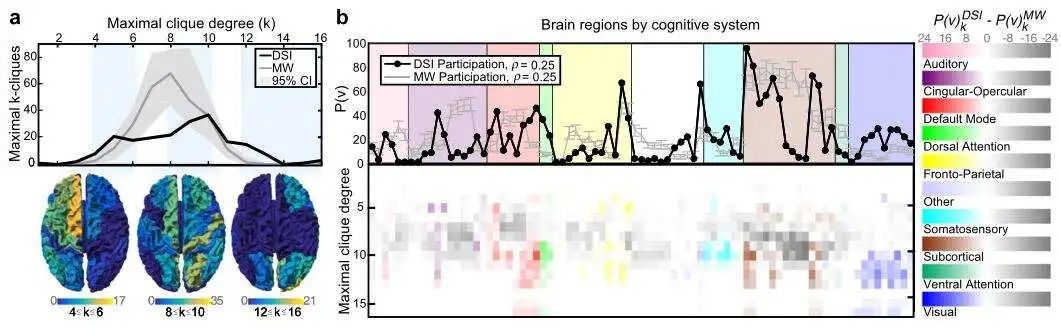 图2:最大团的空间分布在平均脑网络和空模型之间不同。a 为平均扩散光谱成像数据网络(黑色)和单个最小连接(灰色)网络中最大团的分布示意图。b表示按功能成像研究中节点所属的假定认知系统分类下参与最大团示例。
图2:最大团的空间分布在平均脑网络和空模型之间不同。a 为平均扩散光谱成像数据网络(黑色)和单个最小连接(灰色)网络中最大团的分布示意图。b表示按功能成像研究中节点所属的假定认知系统分类下参与最大团示例。
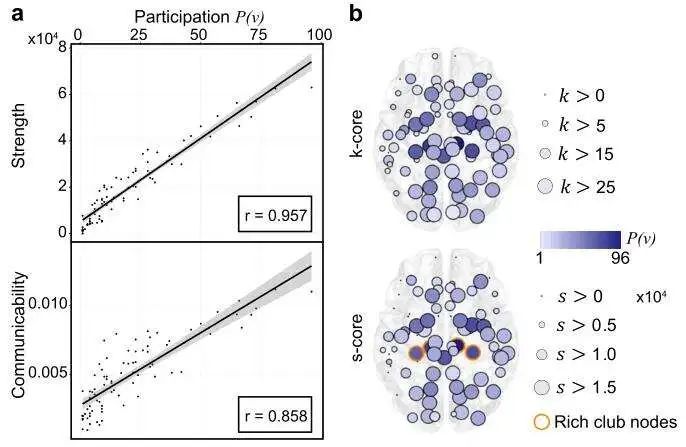
文中还验证了最大k-团的行为与图论度量的一致性。结果表明,通过直接路径和间接游走与大脑其余部分强连接的区域,也参与了许多最大团。在此,利用核心度的概念测量大脑区域与大脑中枢的关联。即G 图的k-核 是图G 的一个极大连通子图,其中所有节点的度至少为k(S-核 表示赋权图的等价概念)。参与度较高的节点通常在k-核 分解中达到较高的级别,并且高参与度节点之间频繁存在丰富的俱乐部联系。这些结果表明,人脑中富人俱乐部区域往往以团的形式参与局部计算。
2. 脑网络中的洞
2. 脑网络中的洞
依据文中描述,不仅扩散光谱成像数据网络中的团可以作为大脑计算结构的邻域尺度构建块,还可以通过研究强连接的缺失来研究这些块之间的关系,即检测大脑网络结构中的拓扑洞。由于连接被视为通信渠道,大脑各区域可以通过这些渠道相互发出信号并参与共享的神经功能,因此缺失此类连接意味着通信能力的降低,这有助于加强不同功能的隔离。
为了识别加权网络中的拓扑洞,作者构建了一个二进制图的序列,每个图都包含在下一个图中(如图4a),被称为过滤(filtration)。从空图开始,按照边缘权重递减的顺序逐一替换未加权的边缘,并通过其边缘密度ρ对每个图进行索引,该密度由图中的边缘数除以可能的边缘数得出。在每条边添加之后,提取k-团的结构,称为无关(k-1)-圈,其中每一个都在结构中包含了一个k维的拓扑洞。这种指数的转变原于几何学:一个2阶团是一个1维的线段,一个3阶团是一个2维的三角形,等等。虽然任何洞都被至少一个圈所包围,但往往是多个圈包围同一个洞。然而,检测同一洞的任何两个(k-1)-圈必然会因为一些(k+1)-团的集合的边界而彼此不同。任何两个这样的环称为拓扑等价圈,因此每个拓扑洞都由一类无关等价圈检测。当通过添加边来进行过滤时,圈的结构,以及其表示的洞结构都会发生变化。图4表示,通过网络过滤模式对团进行追踪,可以发现结构性大脑网络中的关键拓扑洞。
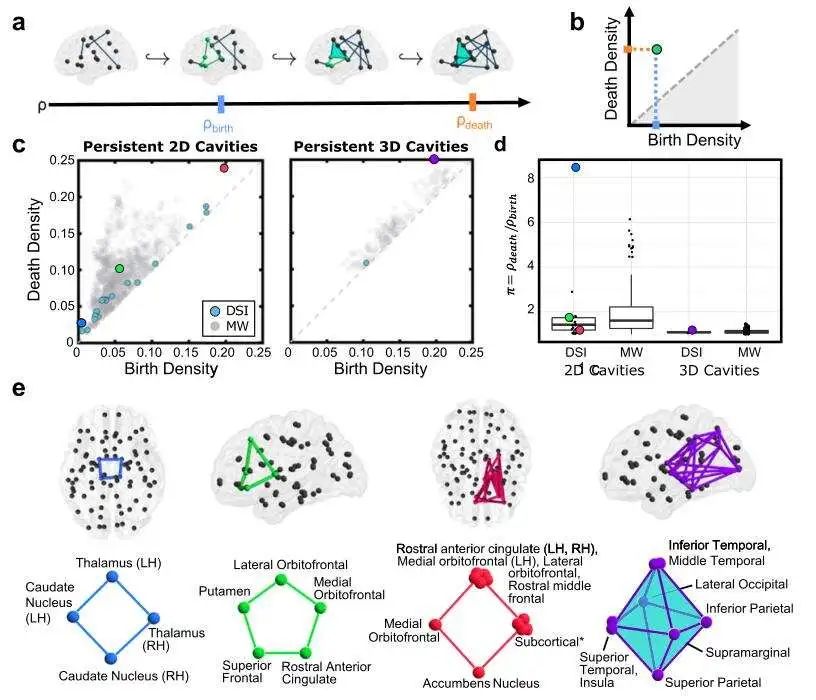
本文研究了组平均扩散光谱成像网络和最小连接空模型网络中二维和三维洞(分别由1阶圈和2阶圈的等效类表示)的持续性。与空模型相比,组平均扩散光谱成像数据网络中的持久性洞明显较少。脑成像数据中最后一个持久的二维洞位于右半球,位于前内侧眶核、伏隔核、任何皮质下区域海马、尾状核、壳核、丘脑和杏仁核之间,以及左半球任何头侧额叶中部、前外侧眶核、前内侧眶核之间,以及来自两半球的头侧前扣带回(所有12个最小代表见图4e)。此外,由3阶团组成的紫色八面体圈包含颞下和颞中、枕外侧、顶叶下、边缘上、顶叶上以及左半球颞上和岛叶中的任何一个,并包围了结构脑网络中寿命最长的三维洞。虽然每一个最小的结构体可能有不同的生物学意义,但作者观察到在周期内皮质下-皮质连接的整体模式。事实上,在20个重构的1阶圈和2阶圈中,有18个包含这个基序。此外,不遵循该基序的两个持续性圈占最小连接网络中持续性圈的三分之一,这表明在这种最大效率的方案中,皮质下环路更可能出现。
3. 可靠性分析
3. 可靠性分析
利用高阶结构分析脑结构网络的拓扑特征,在组平均扩散光谱成像网络中观察到的结构特征,是否也可以在多个个人以及同一个人的多次扫描中一致地观察到,以确保这些洞不是由几个异常值驱动的伪影?
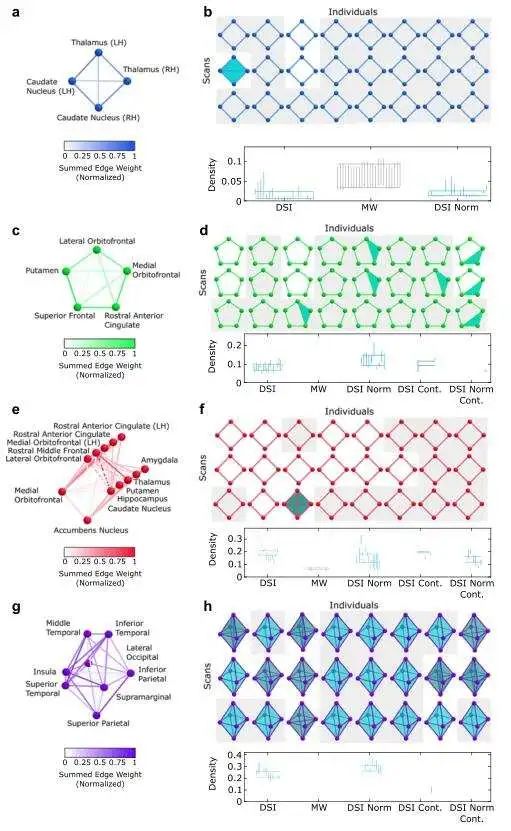
作者为了捕捉平均扩散光谱成像数据中的洞及其最小圈在单个扫描中的存在程度,记录了组成表示等价类的每个最小圈的团的集合 (如图4E所示),并检查是否存在与相同强纤维束的存在相对应的一个团集合,更严格地说,检查每个个体的扩散光谱成像网络中是否存在由该循环表示的拓扑洞。结果证明,在群体平均扩散光谱成像网络中观察到的拓扑洞在个体中表现一致,这也表明它们作为人脑中保守的连接基序具有潜在的作用。
总结
总结
在此文的研究中,为在人脑连接网路中找到可以执行局部计算的密集连接结构,从只考虑成对相互作用转向捕捉更高阶的关系,探讨脑网络中的团和洞结构。使用这种方法验证了,节点在最大团中的参与在空间上和认知系统上都有所不同,这表明这些邻域尺度特征是一种全局体现。并发现重构的拓扑洞在个体间一致存在,在空间嵌入的空模型中不存在,强调了它们在神经布线和功能中的重要性。
该文章首次利用代数拓扑的研究方法,对脑网络中的高阶拓扑进行分析,为脑网络认知提供了一个新的探索方向。随着复杂网络的不断发展,高阶网络以内生的方式,用更简洁的模型描述多主体互动,逐渐成为寻找拓扑特性的重要手段。
高阶网络读书会启动
随着对现实世界的探索不断深入,人们发现在许多真实的复杂系统中,组成系统的个体之间不仅存在二元交互关系,也广泛存在多个体同时(或以特定顺序)进行交互,即高阶交互现象。为此,研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型,为复杂网络分析和研究提供了新的思路。为了促进此领域的交流与合作,我们发起了【高阶网络读书会】。
集智俱乐部读书会是面向广大科研工作者的系列论文研读活动,其目的是共同深入学习探讨某个科学议题,激发科研灵感,促进科研合作。【高阶网络读书会】由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学(北京)管青老师联合发起,第一期分享从 6月 28日(周二)20:00 开始,后续每周分享时间为每周四 19:00-21:00 进行,预计持续 10-12 周。这其间,我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,本次读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。
详情请见:
推荐阅读
-
陈关荣:探讨复杂网络的高阶拓扑及其应用 -
高阶网络动力学综述:同步、传染、合作演化与共识形成 -
Nature Phycics:信息论方法描述高阶相互作用 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会 -
加入集智,一起复杂!