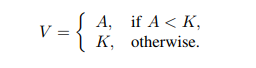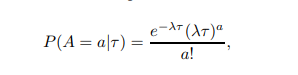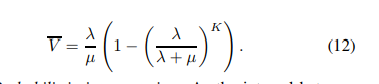导语

信息爆炸时代，注意力是个人最稀缺的资源。从获取信息的角度，多久刷一次朋友圈比较合理呢？问题很复杂，近期一项研究中，研究者把社交媒体的使用问题，简化成了一个数学最优化问题，并给出了如何“高效”刷朋友圈的一个建议：每次刷朋友圈，都请把新信息看完。

看过标题，点进本文，你预期从这篇文章中学到什么了？如果你要的是像42这样明确的回答，那你肯定会失望的。不如你改变期待，看看为何数学模型无法对这个问题给出一个清晰的回答。只有了解不可能性，才能对模型能解决的问题有更清晰的认识。

为什么你投入越来越多时间

在社交媒体上？

从BBS到朋友圈，从头条到知乎，这些平台提供信息流的同时，也依靠信息流中的广告盈利。每个社交媒体网站都期待着你在上面花更多时间，只有这样，才会有更多机会点击广告。

对于普通的社交媒体用户来说，刷朋友圈的间隔越久，积累的新消息越多，若是你还没来得及看完所有消息，部分消息就被你永久错过了，这使得社交媒体对我们的吸引力越来越强。Sean Parker 是社交网站 Napster 的创始人，还曾经是 Facebook公司的联合创始人兼首任总裁，他评价 Facebook 的设计就是为了利用人类脆弱的那一面。

社交网络是否绑架了我们心智？今年4月的Nature Communication的一篇文章指出，新的消息不断竞争着有限的注意力，在群体层面，热点话题留存间隔正在变短。集智俱乐部曾做专文报道，介绍这项研究。

而今年8月，在arixv上8月新出的论文How often should I access my online social networks? （我应该多久上一次在线社交媒体），尝试用数学建模的方式，来回答这个问题。本文将重点介绍这篇论文的核心工作和待改进的问题，并展望未来研究的可能。

论文题目：

How often should I access my online social networks?

论文地址：

https://arxiv.org/abs/1908.04811

模型假设：

社交媒体的5条基本规则

如何回答“多久刷一次朋友圈”的问题，取决于我们怎样假定问题所处的环境，更取决于我们对社交媒体的用户进行怎样的简化。这两个问题是整篇文章方法论的基石，之后的研究若想有所突破，也需要从这个基础出发。

真实世界的社交媒体纷繁复杂，对于社交媒体平台，研究者做出了如下的简化假设：

新内容的产生间隔符合泊松分布（泊松分布描述单位时间内随机事件发生的次数的概率分布）
社交媒体平台会尽可能多地展示新产生的内容
在缺少新内容时，会展示旧的内容

对于社交媒体上的用户，研究者也做出了假设：

用户每次刷新时，最多只会看固定的K条新鲜事
每条新鲜事对用户的价值相同

需要说明的是，研究者关于社交媒体的假设是合理的，但关于用户的假设，则主要是为了简化模型，与真实情况有一定差异。

“刷朋友圈”模型：

用户刷朋友圈收益，取决于新鲜事的多少

站在用户的立场上，应该多久刷一次朋友圈这个问题，是一个最优化问题——刷朋友圈的时间间隔多久，收益最大。

根据对用户的两条假设，可以导出对于用户来说，每次刷朋友圈的收益，当展示的新鲜事的数A小于K的时候是A，否则是K。

之后根据泊松分布，来判断在上次刷朋友之后的τ之后，产生的新鲜事条数是A的概率：

有了概率和收益，就可以求期望。研究者对这个期望在泊松分布的各种可能情况下取全概率分布，就得出了本文提出的核心概念VOA（Value of access，即用户每次的“刷朋友圈收益”），即每次刷朋友圈获得的价值。

模型的建立：特例、极限与参数敏感度

特殊情况是对现实的进一步简化。最简单的情况是，假设总是在固定的间隔刷，这样多久刷一次就完全取决于新鲜事更新的频率。更真实的假设是刷朋友圈的间隔时间呈指数分布，在这种情况下，从刷朋友圈中获得的收益如下式所示：

这里的µ是指数分布的底数，代表每次刷朋友圈的间隔平均为1/u。由于是指数分布，因此在分布上会呈现长尾。即空闲时刷朋友圈的时间隔短，忙碌时刷朋友圈的时间间隔会长一些，越是长期不刷的情况，出现的概率也越低，这符合指数分布。

而极端情况意味着用户对社交媒体使用到了极致。首先当用户单次最大访问信息数K为无穷时，也就是用户会刷完所有的新鲜事，这时平均来看，每个用户每次刷到的新鲜事数量就是λ/µ，其中λ是新鲜事产生对应的泊松分布的期望，1/µ是每次刷的平均间隔。

当新信息的产生速率趋向于无穷大的时候，这时用户刷朋友圈的收益，就取决于他的单次最大访问信息数K，即每次刷朋友圈时最多看几条新消息。而当用户刷朋友圈的平均间隔趋近于无穷大的时候，这时的收益也由K决定。

总结一下这个模型的关键参数，用户的单次最大访问信息数K，新信息产生的期望除以用户刷新的概率λ/µ，之后称为p，其含义是用户每次预期看到多少条新鲜事。

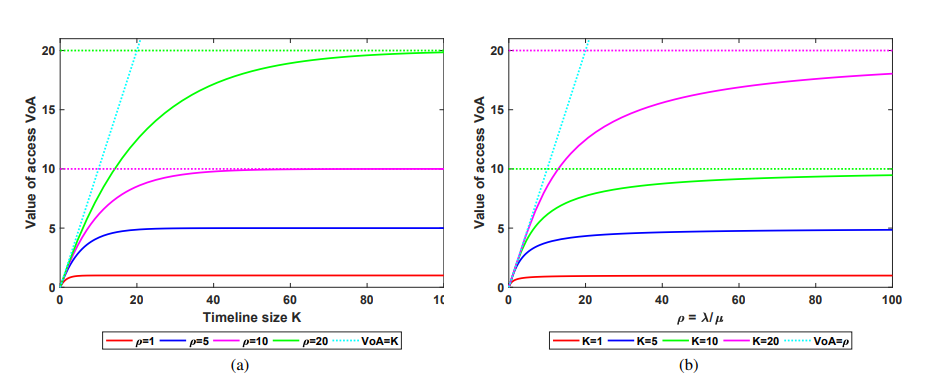
研究者还关注了模型对这两个参数的敏感性，也就是哪个参数的变化，对我们关心的指标VOA（刷朋友圈收益）的影响更大。下图的纵轴是数值模拟中VOA的变化，左边不同的颜色代表不同的p值，右边代表的是不同的K值。

图例：不同参数下的刷朋友圈收益变化曲线

模型验证

之后研究者用巴西大选期间30个媒体账号的Facebook信息流数据，来验证上述模型的假设是成立的。

文中列出的三组验证，第一组是拿信息流去在模拟环境下，用FIFO（最新进入的信息最先推送）来进行模拟，之后是拿网页的插件获取没有登录时下facebook的信息推送，与之对比的是通过插件，获取个人用户登录帐号后，经过facebook的过滤算法推送的结果，以说明Facebook的信息流过滤对用户访问价值的影响。

图例：用真实数据验证模型

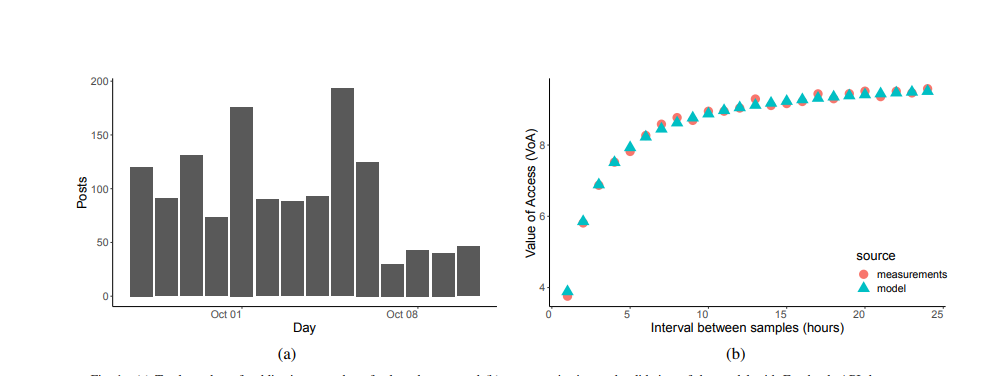
左图是这段时间内一共新产出的内容，横轴是以天计算的时间轴，纵轴是总的推送数。可以看出这里总的推送数加起来也就1000左右，实在算不上大数据研究。

右图比较模型理论计算的VOA（用户每次刷朋友圈收益）的期望值，与通过Bot仿真的到真实的VOA。说明经过参数调优模型，其计算出的期望可以反映真实情况。

批判性地来看，该研究较好地构建了数学模型，但缺点是模型验证有些粗糙。首先，验证数据很少，只来自一种社交媒体，而且集中在一个很特殊的时间段里，得出的结论也有些勉强。这篇文章需要用更大量的数据，且不是在大选这样特殊时间段的数据来做进一步的验证，更高一些的要求是要去比较不同平台，例如 facebook 和 twitter 的数据，以验证模型能够反映各类型的社交网络。

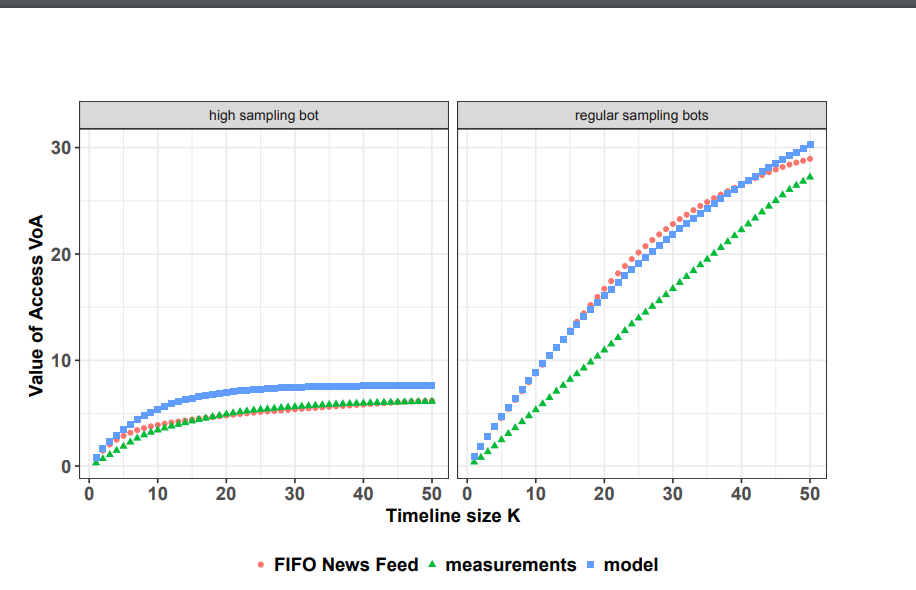
文章指出，用来从社交媒体获取数据的插件分为两种，高频率的每十分钟调取一次，正常的每一小时调取一次。正是这个实验设计上的细微差别，导致了下面的差别。

图例：不同采样频率下的刷朋友圈价值变化曲线

这里左右两图分别比较的是高频采样的和低频采样的Bot，横轴是K的值（用户单次最大访问信息数），纵轴是实际的VOA（用户刷朋友圈价值），左右两图的差距不仅是数量上的，而且结论也不一致了。左图是红色的和绿色的最接近，右图是红色和蓝色的最接近，也就是说这篇文章的结论是和特定的研究方法强绑定的，这是该研究的局限性。

你应该多久刷一次朋友圈

有了要优化的目标VOA（用户刷朋友圈收益），以及需要调整的参数u，就可以回答在理想情况下，刷朋友圈的最佳周期应该符合怎样的概率分布了。

这里作者再引入一条假设：即每次刷朋友圈的成本固定是1，也是一条新鲜事的收益。

这个假设也是比较理想的，有目的地专心刷朋友圈，和在公交车上随意刷朋友圈，实际上是有一定不同的。

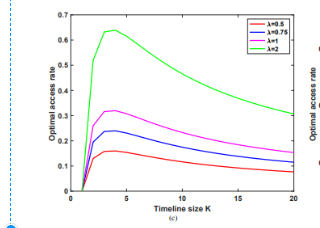
图例：最优刷朋友圈的平均时间随不同参数（k，λ）变化曲线

该图纵轴是最佳的访问频率，不同的颜色代表不同的参数组合，横轴是不同的K值。横轴的K在超过了3之后，其值越大，最优的访问次数也越小，不管新鲜事产生的频率是多少。

这符合生活常识，如果你每次刷朋友圈的时间，只够看一两条新鲜事，那你最好频繁的刷，但如果你每次能够集中一个很长的时间，来看许多条新鲜事，那你应该减少你看新鲜事的频率。

这或许是这篇文章能给读者的最大启示，也就是要想少刷朋友圈，又不漏掉新鲜事，那就要让每次刷的时候多留一些时间，不管有多少条，都看完。

注意力与信息流的未来

注意力经济是集智俱乐部著作《走近2050》这本书中多次出现的概念，也是一个很吸引眼球的话题。虽然说科学研究本身是中立的，但科学家却可以有自己的好恶，研究社交网络上的注意力争夺战，最终的目的是要帮助企业和用户达到双赢。

相关阅读：

信息过载的年代，注意力才是你最稀缺的资源

Nature通信：大规模集体注意力的加速动力学

以知乎为例，自从信息流改版之后，用户默认的推送流就从关注用户，变成了推荐问答和文章，这促成了一次天然的实验：研究者可以去考察用户的访问时长，访问间隔，点赞和收藏数是否由于改版而增加。更关键的是，可以判断用户是否由于推荐算法，浏览了更多和推送前不一样主题的内容，用户的阅读习惯，例如平均阅读文章的长短等是否也发生了变化。

这样的大数据研究，能够说明互联网公司的默认设定对用户的认知习惯所产生的巨大影响，从而为接受信息流的终端用户指出改变方向。对于提供信息流的平台，分析不同策略对用户行为造成的影响，可以判断这样的变化是否在长期上对用户有利，而不是只榨取短期的点击率，从而导致最终用户流失。