导语

根据距离或相似度对数据点聚类，是研究诸多自然和社会问题的有力工具。而在各种聚类算法中，分层聚类具有特别的优势。近日，电子科技大学周涛教授领衔的研究组，在 Information Sciences 杂志发表论文，提出一种新的层次聚类算法。该算法在多领域的数据集中展示出超越同类算法的强大能力，在网络社团检测问题上具有广泛应用前景。

论文题目：

Hierarchical clustering supported by reciprocal nearest neighbors

论文地址：

https://www.sciencedirect.com/science/article/pii/S0020025520303157

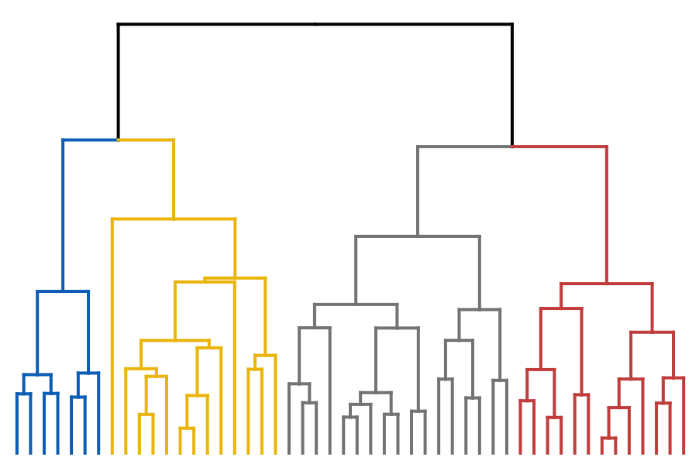
图1：层次聚类算法结果的示意图

传统的聚类算法有很多常见的缺陷，例如需要预先指定聚类的数目（提前知道要聚成几类），又如虽然有了聚类的结果，但是这些类别之间的关系并不明朗。层次聚类算法天然地可以克服这些缺陷。层次聚类算法在最高层面把所有数据点看成一个大类，然后从这个大类中分出几个一级子类，每个一级子类又再分裂出若干二级子类，以此类推。我们不需要提前知道要聚成几类，而且不同子类与子类之间的组织结构非常清晰。图1是一个典型的层次聚类算法的结果，从上到下可以自动得到不同分辨率的聚类结果，且数据点之间的远近亲疏关系都非常清晰。在网络社团挖掘中著名的 Girvan-Newman 算法[4]就是典型的层次聚类算法，这类算法可以得到不同尺度的网络组织方式。当然，层次聚类算法也有很多缺陷，譬如计算复杂度往往较长，受噪音点的影响较大，等等。

假设每一个数据点都喜欢距离自己最近的那个数据点。如果我们从一个数据点 A 出发，依次追逐它喜欢的对象。善良的愿望让我们期望 A 喜欢 B，B 也喜欢 A，但事实往往并非如此，很多时候类似于 A->B->C->D->E 这样很快远离 A，有时候会形成复杂难缠的关系，例如 A->B->C->D->A，甚至是 A->B->C->A。如果非常幸运，存在某对数据点 A、B，满足 A 喜欢 B，B 也喜欢 A，我们就认为这是一对鸳鸯节点（更正式的说法是“互为最近邻”）。

我们提出了一种新的层次聚类算法，其核心假设只有一个，非常善良，就是“棒不打鸳鸯”——互为最近邻的数据点对应该处于同一个类别中。

图2：构建聚类子树的过程示意图

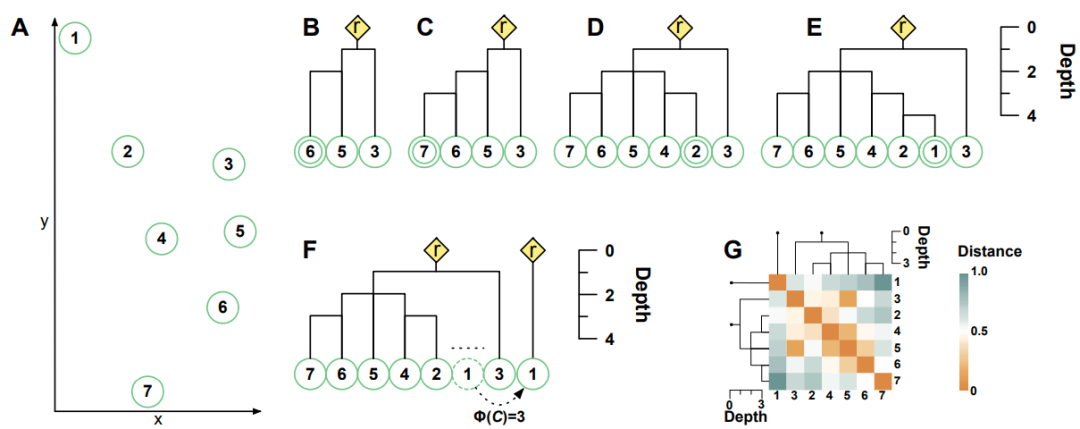
给定了若干数据点且定义好距离，我们首先要做的是构建聚类子树。初始的时候荒芜无树，所有数据点都是自由的。这个时候我们从随机选定的一个自由数据点 A1 出发，找到它喜欢的数据点 A2，然后再找 A2 喜欢的数据点 A3……依次类推，形成一个序列 A1，A2，A3，A4，……。如果存在某个Ai=Ai-2（意味这Ai-2和Ai-1是一对鸳鸯），那么就可以停下来了，这个时候A1到Ai-1构成了一个聚类子树，Ai-2 和 Ai-1 被定义为这个聚类子树的一对支撑节点。我们再加一个虚拟的根节点，它的位置是 Ai-2 和 Ai-1 的“中点”，且同时和 Ai-2 与 Ai-1 相连，就是这个聚类子树的代表点。如果序列A1，A2，A3，A4，……在遇到鸳鸯节点之前就碰到了非自由节点（已经属于某个聚类子树的节点），例如 A4 可能属于另外的子树，则 A1，A2，A3 自动依附到这个已经存在的子树上。如果构成的聚类子树“又瘦又高”，我们会进行剪枝，形成一些孤立节点组成的特殊的聚类子树，它们的代表点就是自己（操作细节请参考原文[5]）。

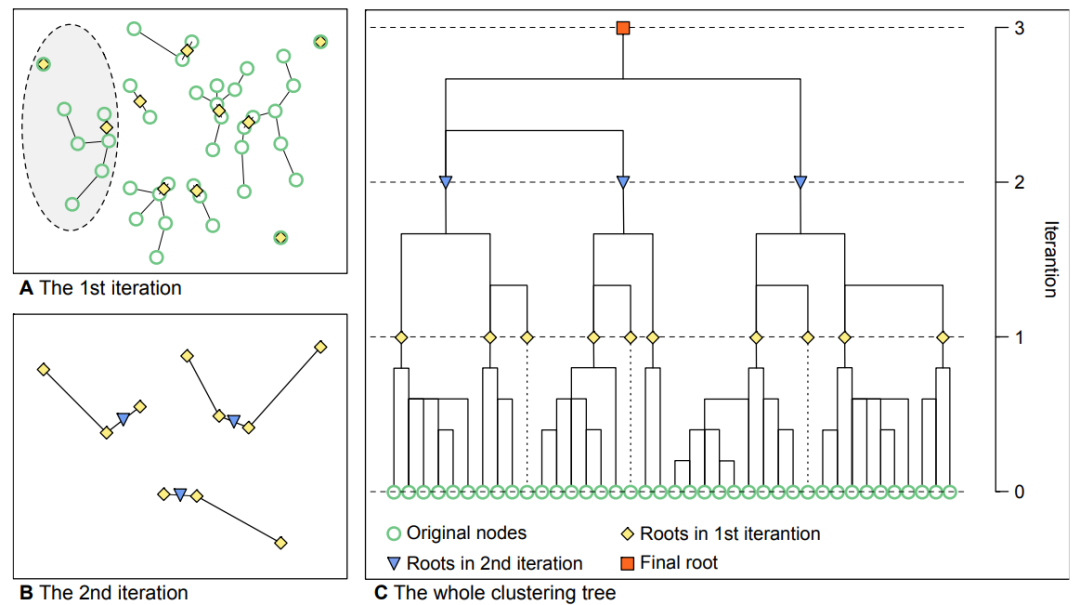
图3：迭代过程示意图

如图3所示，在确定了聚类子树后，我们用这些聚类子树的代表点作为新的数据点，然后可以把刚才的方法继续用于这些新数据点——基于新数据点对之间的距离，我们又可以使用“棒不打鸳鸯”的算法。这样通过迭代的方式，我们就可以获得整个层次聚类的结果。如果数据点所在的距离空间不是欧几里得空间，我们没有办法定义所谓“中点”的位置（譬如某维特征是颜色，距离是海明距离，则我们很难定义绿色和粉色的中点），这个时候我们也可以直接计算“中点”与“中点”之间的距离（具体推导请参考[5]），从而不影响整个算法的实现。

如果有 n 个数据点，利用 K-D Tree[6]可以在 O(nlogn) 时间找到所有最近邻，进而可以证明，在最坏的情况下，本算法的时间复杂度也不超过 O(nlogn)，简要推导如下：

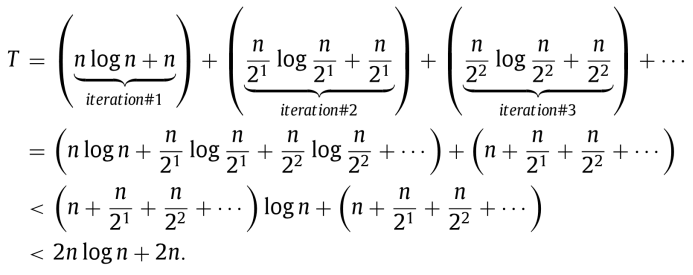
我们基于两个标准数据集，UCI Database 和 Olivetti face data set，测试了我们的算法效果，并和四种有代表的算法，GA[7]、CURE[8]、AP[9] 和 DD[10]，进行了比较。结果显示，我们提出的基于“棒不打鸳鸯”的算法，不仅聚类效果远远显著好于其他算法，而且 CPU 时间也是最短的。

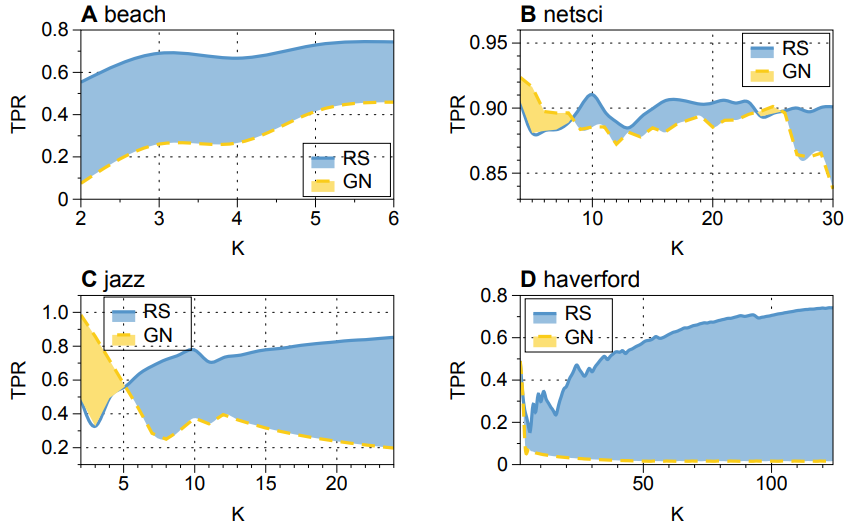
图4：本算法与 Girvan-Newman 算法在社团挖掘任务上的比较

我们还选择了若干被充分研究过且有社团结构“标准答案”的网络，并对比了本算法和 Girvan-Newman 算法在社团挖掘方面的效果。如图4所示，横坐标是划分的社团数目，蓝色阴影部分就是本算法效果好于 Girvan-Newman 算法的情况，黄色阴影部分就是 Girvan-Newman 算法好于本算法的情况。可以看到，在绝大多数情况下本算法是占优的。

如何定义网络上节点之间的距离[11]，以及评估聚类效果（Rand Index [12]）和社团挖掘效果（Triangle Participation Ratio[13]）的参数的具体含义，可以参考原文[5]。

图5：推荐给大家茶余饭后消遣的科普书

对于现在做大数据和人工智能研究的学生、学者和业界人员而言，更时髦的是特征工程和深度学习，数据挖掘单算法的研究已经没有那么性感了。但是我个人特别喜欢这个工作——不仅仅是因为这个算法既快又好，更主要是因为这个算法背后有简单优美的假设：“两个互为最近邻的数据点（节点）应该被分到一个类别中”。毕竟，作为被好奇心驱动的人类，站在黑匣子外面瞻仰它神奇效果的快乐，终归比不上拆解零件洞悉机制的快感。也借此机会推荐我和两位同学最近新写的数据挖掘简明教材（基本上是科普级别的）[1]，里面是数据挖掘最优美算法的集萃，希望大家喜欢。

参考文献：

[1] 周涛，袁飞，庄旭，《最简数据挖掘》(电子工业出版社，2020).

[2] P. N. Tan, M. Steinbach, A. Karpatne, V. Kumar, Introduction to Data Mining – Chapter 7 (Pearson, 2018).

[3] A. K. Jain, Dataclustering: 50years beyond k-means, Pattern Recognit. Lett. 31 (2010) 651–666.

[4] M. Girvan, M. E. J. Newman, Community structure in social and biological networks, PNAS 99 (2002) 7821–7826.

[5] Y.-B. Xie, Y.-L. Lee, C. Wang, D.-B. Chen, T. Zhou, Hierarchical clustering supported by reciprocal nearest neighbors, Information Science 527 (2020) 279-292.

[6] J. L. Bentley, Multidimensional binary search trees used for associative searching, Commun. ACM 18 (1975) 509–517.

[7] J. H. Ward Jr., Hierarchical grouping to optimize an objective function, J. Am. Stat. Assoc. 58 (1963) 236–244.

[8] S. Guha, R. Rastogi, K. Shim, Cure: anefficient clustering algorithm for large database, Inf. Syst. 26 (2001) 35–58.

[9] B. J. Frey, D. Dueck, Clustering bypassing messages between data points, Science 315 (2007) 972–976.

[10] A. Rodrigue, A. Laio, Clustering by fast search and find of density peaks, Science 344 (2014) 1492–1496.

[11] F. Fouss, A. Pirotte, J. M. Renders, M. Saerens, Random–walk computation of similarities between nodes of a graph with application to collaborative recommendation, IEEE Trans. Knowl. Data Eng. 19 (2007) 355–369.

[12] W. M. Rand, Objective criteria for the evaluation of clustering methods, J. Am. Stat. Assoc. 66 (1971) 846–850.

[13] J. Yang, J. Leskovec, Defining and evaluating network communities based on ground-truth, Knowl. Inf. Syst. 42 (2015) 181–213.

（参考文献可上下滑动）