“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

本文是对集智百科中“耗散系统”词条的摘录，参考资料及相关词条请参阅百科词条原文

一、什么是耗散系统？

二、热力学中的耗散结构

三、控制论中的耗散系统

四、量子耗散系统

五、相关资源推介

六、集智百科词条志愿者招募

一、什么是耗散系统？

耗散系统 Dissipative system 是一种远离热力学平衡的热力学开放系统，运行在与之交换能量和物质的环境中。例如，龙卷风可以被认为是一个耗散系统。耗散结构 Sissipative Structure 是一种耗散系统，其动力学性质在某种意义上是一种可重复的稳定状态。可以通过系统的自然进化、使用技巧来进化或两者的结合来达到这种可重复的稳定状态。

耗散结构的特点是自发出现对称性破缺（各向异性）和形成复杂的、有时是混沌的结构，在这些结构中，相互作用的粒子展现出长程关联的性质。日常生活中的例子包括对流、湍流、旋风、飓风和生物体。较少见的例子包括激光、b 细胞、液滴簇和BZ反应 Belousov–Zhabotinsky reaction。

耗散系统也可以作为研究经济系统和复杂系统的工具。例如，一个包含纳米线自组装的耗散系统被用作理解熵产生和生物系统鲁棒性之间关系的模型。

二、热力学中的耗散结构

耗散结构一词是由俄罗斯-比利时的物理化学家伊利亚·普里高津 Ilya Prigogine 发明的，他因在耗散结构方面的开创性工作获得了1977年的诺贝尔化学奖。普里高津所考虑的耗散结构具有可被视为热力学稳态的动力学性质，有时至少可以用合适的非平衡态热力学中的极值定理来描述。

图1：伊利亚·普里高津 Ilya Prigogine

在他的诺贝尔演讲中，普里高津解释了远离平衡的热力学系统如何与接近平衡的系统有着截然不同的行为。在平衡点附近，采用局部平衡假设，并可局部定义自由能和熵等典型热力学量。我们可以假定系统的（广义）通量和力之间是线性关系。线性热力学的两个著名成果是昂萨格倒易关系 Onsager reciprocal relations 和最小熵产生定理 the principle of minimum entropy production。在努力将这些结果推广到远离平衡的系统之后，人们发现它们在这个系统中不成立，并且得到了相反的结果。

严格分析此类系统的一种方法是研究远离平衡的系统的稳定性。接近平衡点时，我们可以证明存在李雅普诺夫函数 Lyapunov function，它确保熵趋于稳定的最大值。波动在固定点附近被阻尼，宏观描述就已足够。然而，远离平衡的稳定性不再是一个普遍的性质，并且可以被打破。在化学系统中，这是在存在自催化反应的情况下发生的，例如在布鲁塞尔模型 Brusselator 中。如果系统被驱动超过一定的阈值，振荡不再被阻尼，而是可能被放大。从数学上讲，这相当于一个霍普夫分岔 Hopf bifurcation，其中一个参数增加超过一定的值会导致极限环行为 limit cycle behavior。如果通过反应扩散方程来考虑空间效应，就会产生长程关联和空间有序模式 spatially ordered patterns，例如BZ反应 Belousov–Zhabotinsky reaction。由于不可逆过程而产生的具有这种物质动态状态的系统是耗散结构。

三、控制论中的耗散系统

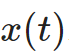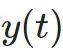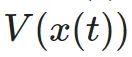Willems首先在系统理论中引入耗散性的概念，用输入输出特性来描述动力系统。考虑一个由其状态、输入和输出所描述的动力系统，输入-输出的相关性被给出了供给率。如果存在一个连续可微的存储函数，使得,且，则系统对于供给率来说是耗散的。

作为耗散性的一个特例，如果上述耗散性不等式对于被动供给率成立，则称系统为无源系统。

物理解释是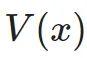，是储存在系统中的能量，而是供给系统的能量。

这个概念与李雅普诺夫稳定性 Lyapunov stability 有很强的联系，其中，在动力系统能控性和可观测性一定的条件下，存储函数可以起到李雅普诺夫函数 Lyapunov functions 的作用。

粗略地说，耗散理论对于设计线性和非线性系统的反馈控制律是有用的。V.M.Popov、J.C.Willems、D.J.Hill 和 P.Moylan 讨论过耗散系统理论。在线性不变系统中，这被称为正实传递函数 Positive real transfer functions，一个基本的工具就是所谓的 Kalman-Yakubovich-Popov引理 ，它关系到正实系统的状态空间和频域特性。由于其重要的应用，耗散系统一直是系统与控制领域的研究热点。

四、量子耗散系统

由于量子力学，以及所有经典的动力系统都严重依赖于时间可逆的哈密顿力学 Hamiltonian mechanics，因此这些近似在本质上不能描述耗散系统。有人提出，原则上，人们可以将系统（例如，一个谐振子）弱耦合到热源 bath中，也就是说，针对一组在热力学平衡态下，具备较宽的频谱的多个谐振子的集合，并对它们在所有的热源中取迹（平均）。这就产生了一个主方程，这是一个较为普遍的情况下的特例，被称为林德布莱德方程 Lindblad equation，它是经典刘维尔方程 Liouville equation 的量子等价物。众所周知，这个方程和它的量子对应物把时间作为一个可逆变量来积分，但耗散结构的基础认为时间具有不可逆且建设性的作用。

耗散结构框架作为一种理解系统在能量不断交换中的行为的机制，已经成功地应用于不同的科学领域和应用，如光学、种群动力学、生长和化学机械结构等。