生活中的等级现象几乎无处不在，而你是否思考过什么因素导致了等级的出现？“胜利者效应”（winner effect）或许可以给予灵感，即人在有利的活动中获得认可则会增加他们在未来活动中获胜的可能性。近日 PNAS 上的一项研究受胜利者效应启发，提出了一个兼顾数学分析和统计推断特点的适应性社会等级网络模型，以解决等级关系的塑造与维系问题。
期刊来源：PNAS
Emergence of hierarchy in networked endorsement dynamics
https://www.pnas.org/content/118/16/e2015188118
等级是许多人类和动物社会中个体间的稳定关系。动物可利用等级决定获取食物、繁殖等资源的途径，而人类也可以利用等级获得资本与机会。尽管等级关系无处不在，但目前针对这种现象的产生及维系的解释尚少。
“胜利者效应”（winner effect）或许可以为此带来启发。“胜利者效应”是指已获胜的经历会提高下一次获胜的概率，而理论研究和人体对照实验都表明，“胜利者效应”足以形成稳定的等级制度。其中一种解释是每个人都拥有一种“内在力量”，这可能取决于诸如体型、技能或攻击水平等因素。例如，在2017年浙大胡海岚团队在 Science 上发文，表明成功经历或许正在改变获胜者的大脑，让他在下一轮竞争中更易获胜。
图1. 浙大胡海岚团队Science上发文，揭示“胜利者效应”的脑机制（History of winning remodels thalamo-PFC circuit to reinforce social dominance（2017））。
然而，这些内在的因素并不是产生“胜利者效应”的必要条件。比如竞选者们在前期的支持拉票中为自己的候选资格夯实基础，这可能导致未来在选举种获得胜利。对于竞选者、代言人们等，他们的知名度是关键，知名度越高意味着其代言价值越高，相对等级也就越高。研究者们把这种知名度或信任度是称作“传递性威望”（transitive prestige）。
人与人互动间的传递性威望逐渐导致了等级制度，而借助网络可以来研究各个主体的角色。最近的实证研究强调了生物和社会群体中等级的网络化本质，一些理论研究也使用“自适应”的时变网络模型来加强层次。在这类模型中，相连通的边随着节点状态变化而变化，反之亦然。边趋向于聚集到关键节点，从而导致自我强化的层次网络结构。
图2. 社交网络中人们倾向于关注知名度或权威性更高的人
在该研究的自适应网络模型中，新的有向边的产生基于已有的节点和节点间层次结构，之后这些边会随着时间的推移而衰减。有向边i→j概念化为获胜或认可，即j胜过i，或j得到i的认可。n个节点之间的关系可以用邻接矩阵A表示，其中每个元素aij表示两个节点之间的认可程度。
该网络的邻接矩阵A根据下方表达式随时间改变。其中Δ(t)表示t时刻下新产生的获胜关系，“记忆因子”λ∈[0,1]反映获胜关系的维系时间长短，λ越小则代表该获胜关系越容易被“遗忘”。这是本文提出的时变网络模型的一般形式：
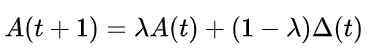
新的获胜关系Δ(t)取决于曾经的获胜经历。通过相关节点排序算法中的得分计算函数（score function）σ:A→s可以计算i个节点的得分（score）S，进而得到各个节点的等级排序。该研究中采用的得分计算函数包括：Root-Degree、PageRank和SpringRank三种。
已知得分 S 后，基于现状获胜关系可以通过随机效用模型获取新的获胜关系Δ，具体表示为：
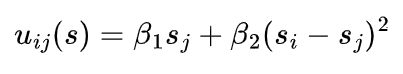
其中一般假设β1>0和β2<0。参数β1捕获了“威望偏好”，β1值为正表示倾向于认可高分者。参数β2反映为“接近偏好”，β2值为负值，表明倾向于认可与自己得分相近的他人。最后获胜关系i→j产生的概率为可由多项Logit表示：
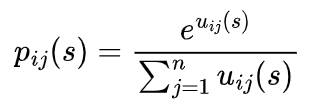
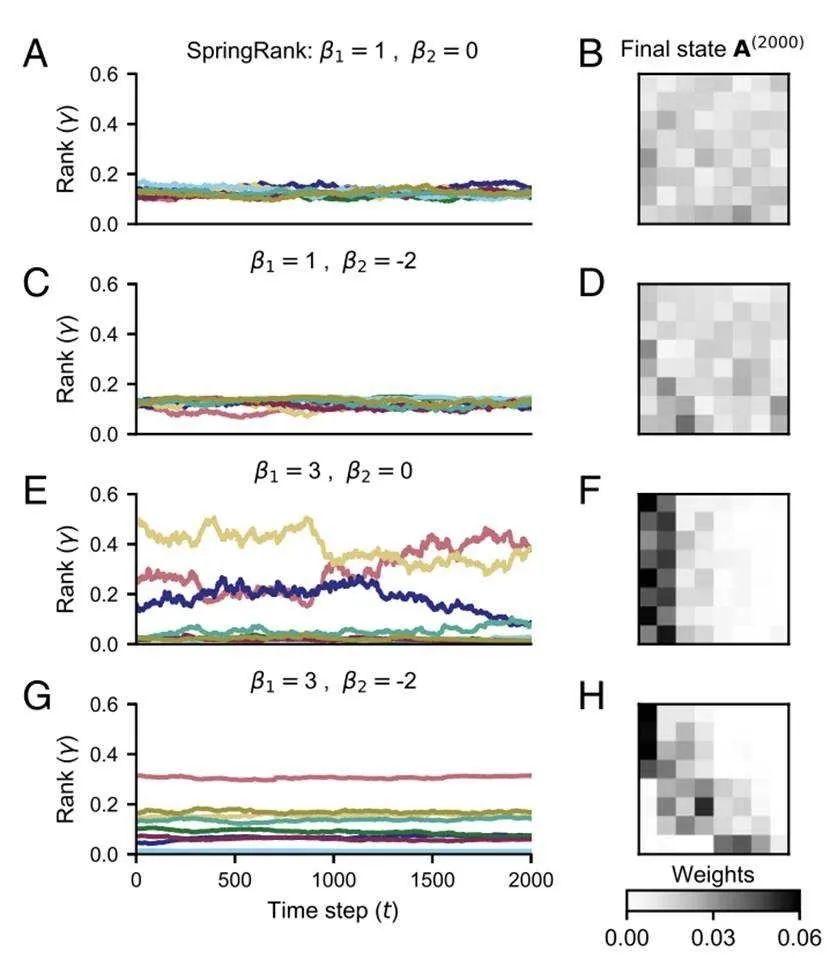
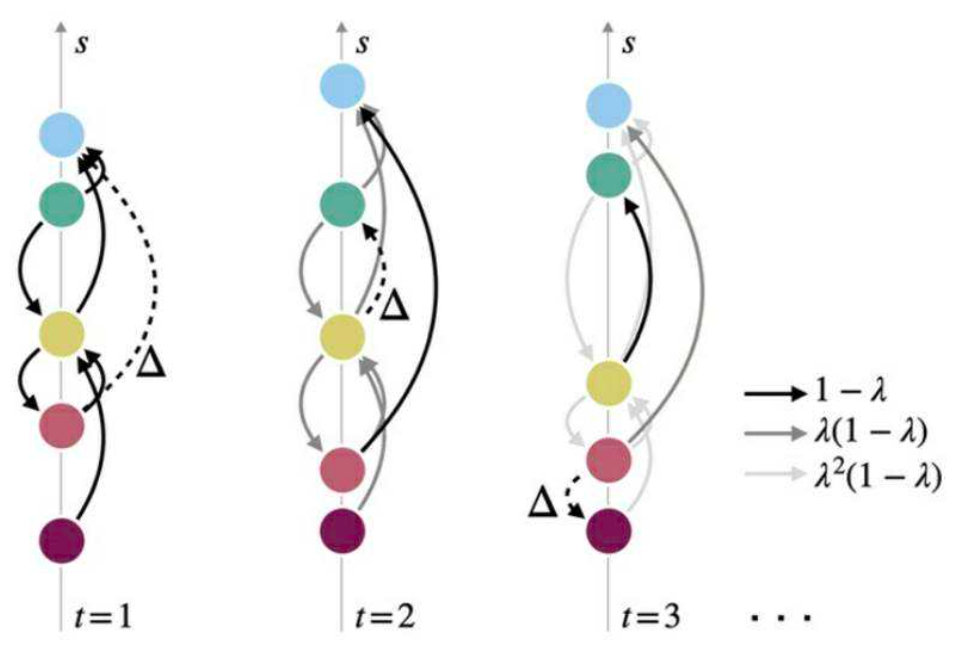
图3是该研究提出的“获胜”动力学与等级演变示意图，反映了5个节点在时间范围内等级的相对变化情况。横轴t代表不同时刻，纵轴s代表等级评分，在纵轴的位置越高意味着等级越高。虚线Δ代表t时刻下新产生的获胜关系。实线代表已存在的获胜经历，而不同深浅色的实线则反映时间变化情况下获胜关系的衰减情况。颜色越浅代表该获胜关系越“被遗忘”，或是不再那么重要。
这里引入“等级向量”（rank vector）γ的概念，它的第j个元素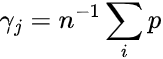 
表示新的指向第j个节点的可能性。如果当所有的γj相等，则此时状态是平等的，否则是有等级存在的。
图4中左侧（子图A、C、E、G）表示在不同β1和β2下等级向量的变化情况，不同的颜色跟踪不同节点的等级。右侧（子图B、D、F、H）表示在t=2000时的邻接矩阵。对比子图C和G，子图G中的等级分化更加明显。β1较小时“胜利者效应”较弱，整体近似平均主义。对于更大的β1，会有更明显的赢家效应。在文章中求得了评分函数下β1对整体等级演变带来剧变的临界值。当对高等级节点的偏好超过一个临界值时，平等主义的状态就会不稳定，等级制度就会出现。这个转换的位置取决于得分函数的结构和节点的初始状态。
而β2的影响似乎更体现在排名的稳定程度上。从图4子图E和G即可看出偏小的β2能减少网络中等级演变的波动，使网络等级演变更加平稳。
在该研究中选取了四组真实数据进行模型评估，分别是：数学学术交流网络，两个长尾小鹦鹉互动网络，以及一个兄弟会成员之间的友谊网络。其中的获胜关系i→j可以分别对应着：学校i的师生被招聘到学校j、鹦鹉j战胜鹦鹉i、兄弟会中成员j被成员i视作好朋友。
图5. 不同的评分函数可能导致不一样的等级演化状态
研究分别使用root degree、PageRanks和pringank评分函数对这些数据进行了分析。尽管如图5所示，对于不同的数据有着不同的最适合评分函数，但总结三种评分函数得到的参数估计、SEs以及优化得到的对数似然值，有如下几个特点：β1>0和β2<0可以反映在等级演变中的一种持续模式——虽然获胜关系的确会向高等级的节点流入（β1>0），但节点更可能真正产生关联的是那些在等级上接近它们的（β2<0）。这种认可或获胜关系往往会往上升几级，而不是直接关联到最高层。
在数学学术交流网络中，由于精英有限，排名偏低的学校很难招聘到排名高的学校的师生。在长尾小鹦鹉种群中，邻近水平的相互攻击可能通过传递威望以促进对统治等级的巩固。在兄弟会关系中，内在的社会规范可能驱使地位相似的人相互为伴。因此，虽然我们在参数估计中没有将这种模式归因于一种普遍的机制，但研究者们认为它这种等级的长期性将是未来研究的有趣课题。
这篇文章提出了一个简单而灵活的、长期的等级演化模型。当对高等级的偏好超过某个临界值时，平等主义的状态就会不稳定，等级制度将会涌现。该研究结果强调胜利者效应不需要内部因素，通过传递性威望而产生的社会强化足以导致社会等级的产生。
该时变网络生成模型在未来仍有改进空间：（1）扩展现有的基于网络的模型，以便从数据中统计了解它们的参数，这将使不同建模框架能够进行比较验证。（2）研究时间依赖的中心度和动态层次模型之间的关系也将是未来研究的趋势。特别是，时变中心理论（the theory of time-dependent centralities）面临着一个重要的方法论问题:不同的合理排序方法在应用于同一数据集时，会产生方向性不同的节点排序，预测传播过程中的中心节点同样重要。（3）好的中心性度量指标能够最有效地预测系统未来发展。在这个方向的进一步研究可以揭示不同形式的中心性度量如何来控制网络的进化。
集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：
点击“阅读原文”，追踪复杂科学顶刊论文
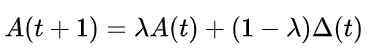
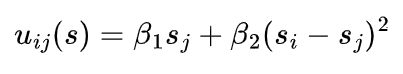
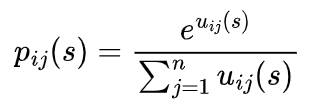
