图模型与因果推理基础- SCM框架和Do-Calculus

导语
本文主要串讲了Pearl因果识别框架的基础知识,包括图模型、结构因果模型的范式,三种识别策略,以及如何运用do- calculus的三种规则来进行因果识别。本篇内容整理自因果科学读书会第一季。
集智俱乐部联合智源社区,组织因果科学系列读书会第二季,从基础和实操角度出发,精读两本因果科学方向的入门教材。详情见文末。

付鑫玉 | 作者
邓一雪 | 编辑
“年轻人到底该不该搞副业?”
最近,随着“斜杠青年”、“自由职业”等概念的兴起,受益于“猪八戒”等众包平台,有一技之长的年轻人纷纷开始搞副业,兼职翻译、配音朗读、程序员做开发、P图手绘,或者自己做自媒体,分享美妆护肤、投资理财、下厨做饭等技巧,我身边也有很多朋友心里痒痒,就拿做开发的程序员朋友来说,有的人觉得在一些平台上接私活能够精进开发能力、接触到新流程,又可以将自己的兴趣和特长转化为金钱;也有的朋友对此持保留态度,如何不打算把副业当作全职,那么下班时间就应该好好休息,放松自己,或者多思考跟本职工作有关的事情,“搞副业”反而可能耽误主业,影响升迁。那么问题来了,“搞副业”对于一个人的主业职业发展究竟有没有影响?换句话说,我们是否能够证明“搞副业”会导致主业职业发展变得更好,或者更坏?
如果你曾经上过计量经济学的课,或者阅读过之前集智俱乐部发布的关于因果效应的文章,或者你会很自信地说,这是一个典型的通过观测数据进行因果效应发现及评估的问题。传统意义上,通过手动推导和测试各种模型,我们可以解决包含少量变量的因果推理问题,然而,随着数据科学的兴起,我们现在往往需要从一个包含成百上千变量的数据集中推断和评估因果效应,变量的关系错综复杂,因此,一个可以自动化进行因果推理的演算应用框架 – 结构因果模型(Structural Causal Model )及do-calculus应运而生。本文旨在通过实例及模拟数据,串讲Judea Pearl的因果理论基础知识。
1. 搞副业会影响你的主业吗?
为什么我们需要图模型和结果因果模型
1. 搞副业会影响你的主业吗?
为什么我们需要图模型和结果因果模型
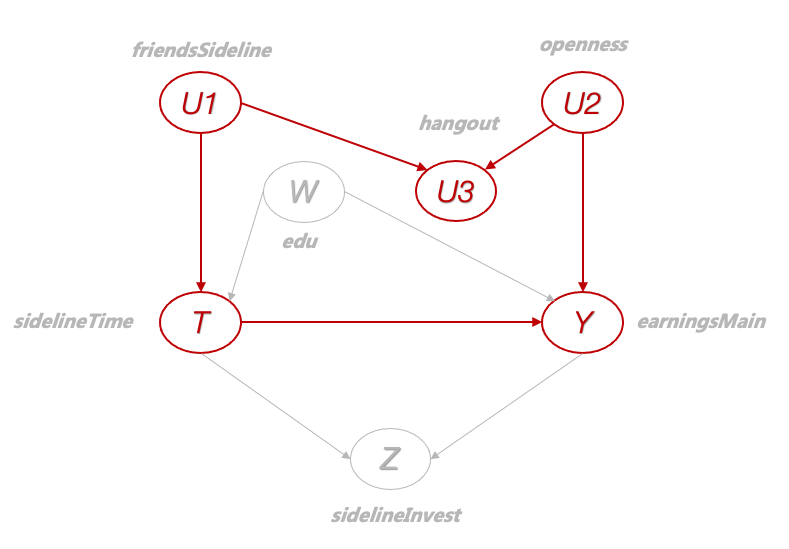
想象一下现在你手头拿到一个关于打工人职业发展、升职加薪的数据,里面有一系列变量,教育背景 、性格特征、社交情况(如每月出门玩的小时数)、在副业投入的时间、身边做副业朋友的数量、副业设备投入(比如升级装备,购买更好的相机、电脑等)、以及主业收入。我们感兴趣的自变量是在副业投入的时间,因变量是主业收入,其他协变量既包括个体的自身情况(如教育背景、性格特征、社交情况),也包括和研究问题密切相关的变量(身边做副业朋友的人数多少、在副业设备升级的投入)。这些变量理论上都有关联,比如教育背景和性格特征会影响一个人的收入,教育背景也会影响个体有意愿、有能力选择进行副业投入的时间,身边做副业朋友的数量会影响个体对于副业的时间投入,个体的收入和副业投入程度会影响其对于升级副业所需设备的投入,等等。假设我们只有横截面数据,现在你想要探索副业投入(T,sidelineTime)对收入(Y, earningsMain)的影响方向及大小,并且拥有如图中所示的五个协变量,你会怎么做?
Figure 1 变量概览
你可能会说,这很简单,先看看变量之间的相关性,然后跑个回归看看,比如假设以下模型:
earningsMain=(β0+β)1sidelineTime+β2edu+β3hangout+β4openness+β5friendsSideline+β6sidelineInvest+ε
然后你得出结论,其他条件不变的情况下,每一个单位sidelineTim的变动,会引起β1个单位earnings的变动。但是,这个结论真的正确、无偏、具有因果性吗?对于数据中的每一个变量,我们是否可以“无脑”把它们都加进模型里呢?
我们可以用一些模拟数据进行验证:假如我们开了“上帝之眼”,知道世间万事万物的因果关系,包括因果方向及其影响大小,我们假设以上变量服从以下因果关系(请注意下图中的箭头指向):
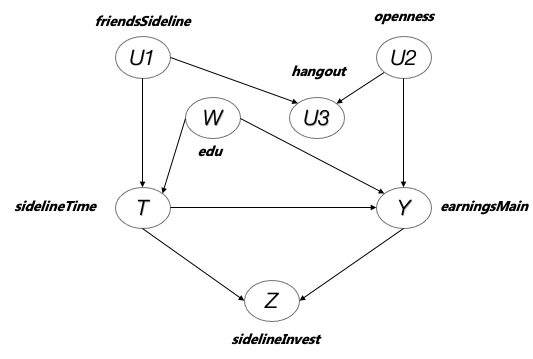
Figure 2 变量因果关系图
该图中,我们可以看到,副业时间投入(sidelineTime)对于主业收入(earningsMain)有因果影响。具体来讲,副业时间投入收到身边做副业朋友的数量(friendsSideline)和个体教育背景(edu)的影响;主业收入收到教育背景和个体性格开放性(openness)的影响;副业时间投入收到身边做副业朋友的数量(friendsSideline)和个体性格开放性(openness)会影响一个人平均每周可以结识新朋友的数量(newFriendsPerWeek),但结交新朋友数量对于副业时间投入(sidelineTime)对于主业收入(earningsMain)都没有直接因果影响;最后,副业时间投入(sidelineTime)对于主业收入(earningsMain)均对副业设备升级投入(sidelineInvest)有因果影响。
我们首先在R中生成一些虚拟数据,如图4和图5所示。不过具体代码不重要,重要的是:
(1)我们现在开了上帝之眼,命令sidelineTime和earningMain之间的因果关系为正向,且大小为1.2,即其他条件不变的情况下,sidelineTime每增长一单位,主业收入增加1.2个单位:
earningsMain=1.2sidelineTime+0.6edu+0.3openness+ε
(2)类似地,我们也定义了其他变量之间的关系,表示变量之间相互因果关系的系数如下图所示:
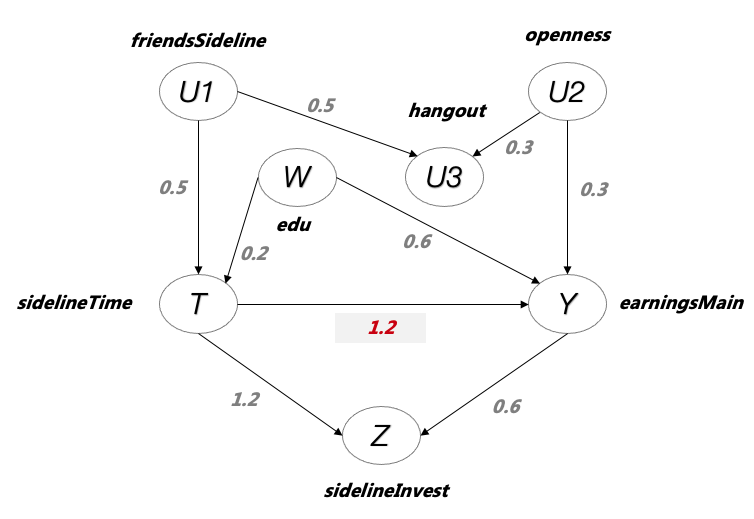
Figure 3 变量因果关系图,含系数
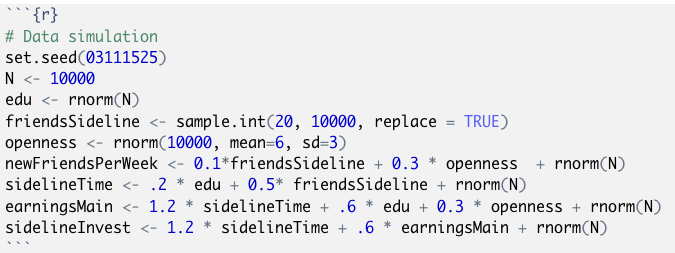
Figure 4 用R生成模拟数据
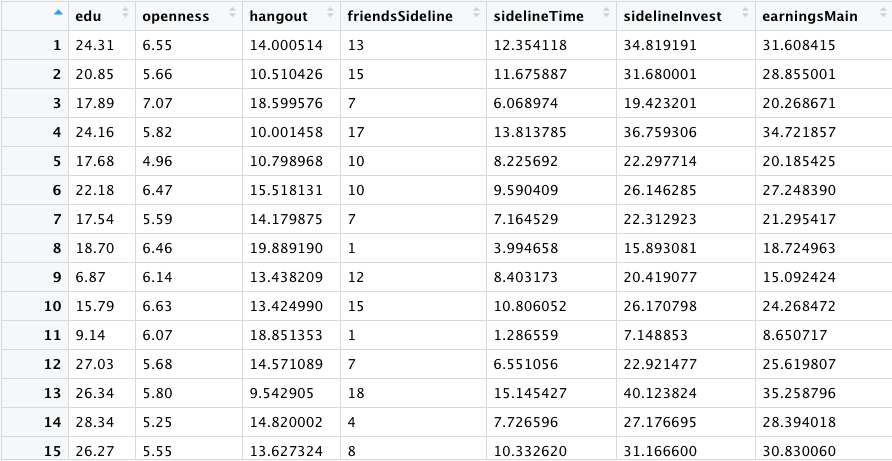
Figure 5 模拟数据概览
(3)因为数据是我们生成的,我们开了“上帝之眼”,知道我们关系的因果关系大小为1.2。那么,在所有可能的模型里,只有最终等于或者无限接近1.2这个数值的模型才是最可能正确的模型。换句话说,只有正确的添加变量在模型中,我们才能得到正确的因果关系估计。
现在我们再来问一次,如果我们已经知道了所有的这些因果关系导向,你认为哪些变量应该被放入模型中?在下列这些可能的模型中,你认为哪个模型是合适的?

Figure 6 可供选择的一些模型
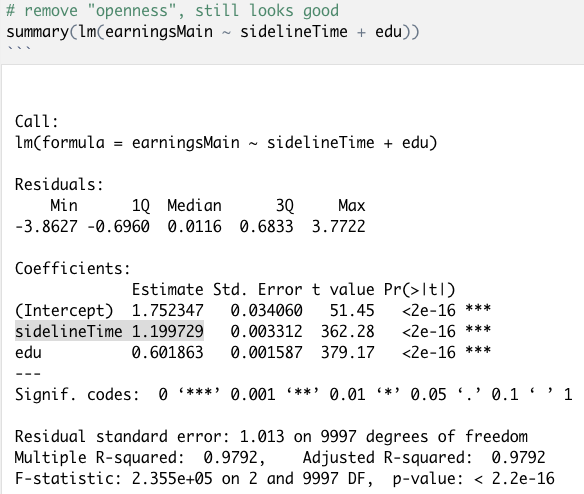
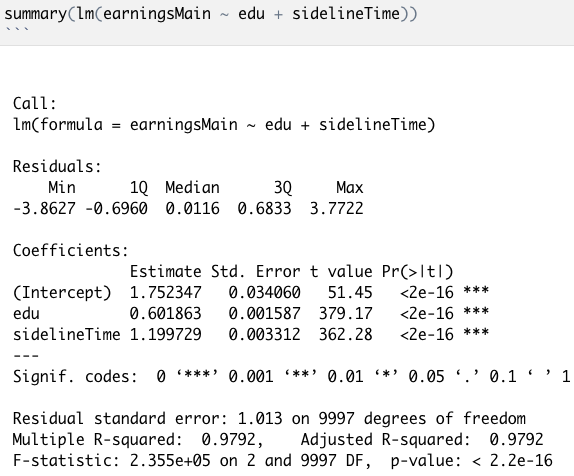
可以看到,模型(1)是最基础的选择,但是只包括sidelineTime,而忽略其他对earningsMain有因果影响的变量,会导致高估sidelineTime对earningsMain的影响;相反,模型(2)将所有的可用变量都放进模型中,不但没有带来有效信息,反而增加了更多的干扰(noise),结果估计也不准确;此处列举四个比较有代表性的模型及其结果,红色方框圈出了该模型下对于sidelineTime对于earningsMain的因果效应估计,其中,越接近1.2真实值表示该模型越接近“真相”。一般来说,我们会很自然地想到把有指向earningsMain的变量们都加入到模型里,事实上,如下图所示,这样得到的结果非常接近真实值1.2:
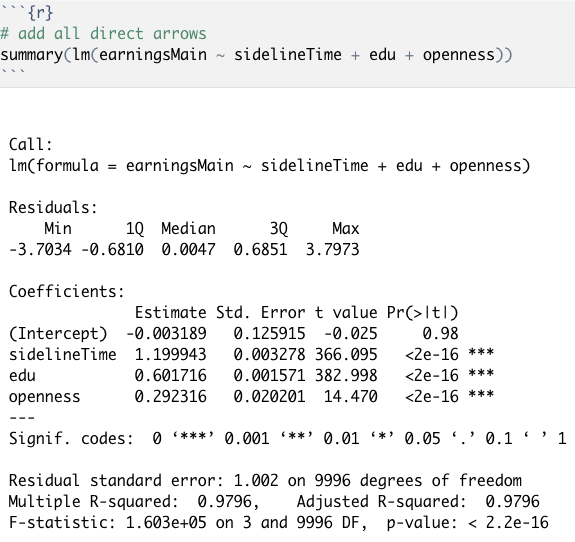
Figure 7 模型(4)对应的结果
然而,一旦在模型中加入了“sidelineInvest”,预期的因果效应变成了0.3317,被严重低估了:
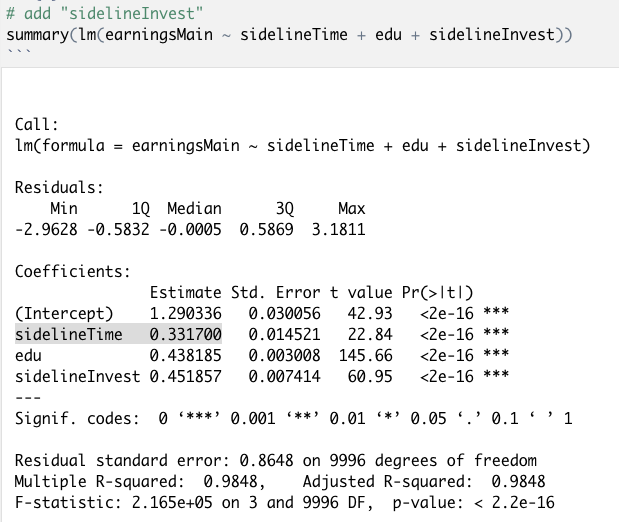
Figure 8 模型(5)对应的结果
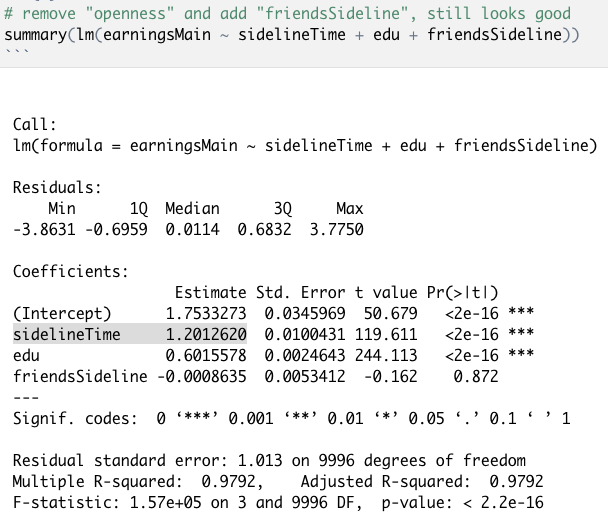
此外,即使少加一些、或者多加一些变量,似乎也对因果效应估计的结果没有产生很大影响:例如图8(a)s去掉了openness,只保留了edu作为协变量,结果估计依然非常接近1.2的真实值;而图8(b)-(d)引入了其他的非直接与主业收入相关的变量(如hangout,friendsSideline),他们的结果虽然不同程度地离1.2真实值有更大的偏差,但基本还算准确。但为什么这些模型也基本可以满足我们对于因果效应估计的需求呢?
|
|
|
|
Figure 8 (a) |
Figure 8 (b) |
|
|
|
|
Figure 8 (c) |
Figure 8 (d) |
Figure 9 部分模型结果,从左上到右下分别对应模型3,6,7,8
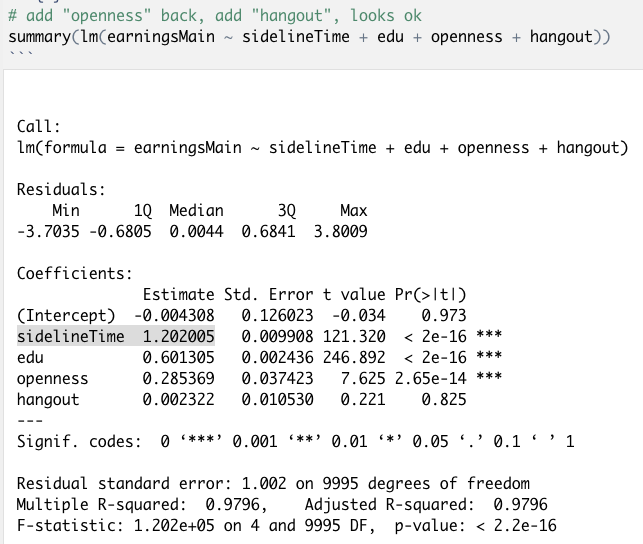
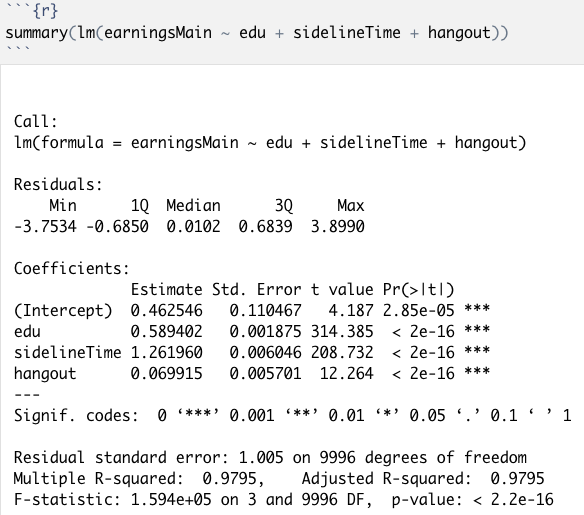
然而,模型(8),也是去掉了openness,加上了hangout,却导致因果效应的估计结果陡然增加到1.261960,距离真实值出现了巨大的偏差,这又是什么呢?
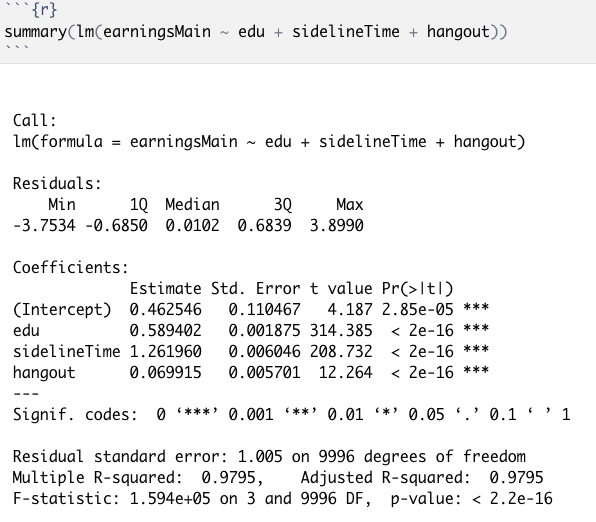
Figure 10 模型(8)对应的结果:出现了很大的估计偏差
让我们暂时保留这两个疑问。这个例子还可以变得更复杂一点:现实生活中,有很多变量都不可观测,或者不好测量,比如在本例中,开展副业的朋友数量不便统计,对于性格开放性的测试也难以大规模获取,在图10中,我们用虚线圆圈表示这两个变量现在成为了不可观测的变量,在这种情况下,我们又该如何正确估计开展副业对于主业收入的因果关系呢?
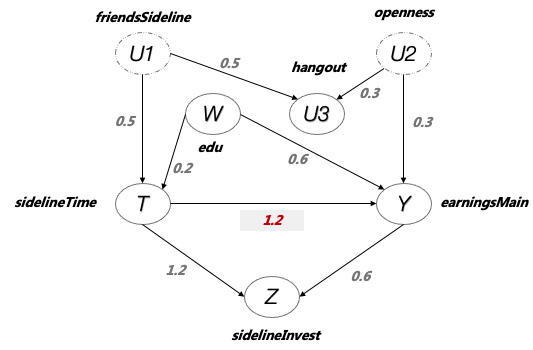
此时,由于friendsSideline和openness变成了隐变量,我们目前可选择的协变量还剩下edu,hangout,和sidelineInvest三个。首先,我们尝试把hangout加进模型里,同之前一样,我们会发现此时估计的结果出现了很大的误差,从1.20到了1.26。反而把hangout去掉,如图13所示,使得我们在有不可观测变量的情况下依然得到了近似无偏的估计。这个例子告诉我们,即使有些变量是无法观测、没有获取的,我们依然有办法可以正确推断T到Y的因果效应。
在本例中,我们的目标是估计从事副业对于主业收入的因果效应。通过不同的模型结果,我们可以体会到,在实际数据分析过程中,是否选择某一个或一组协变量,会对因果效应的估计结果产生很大的影响。那么,在不知道数据实际生成过程的情况下,我们该如何选择变量、进行正确的因果效应估计呢?有没有一些技巧可以帮助我们判断呢?如果有的话,这些技巧在不可观测/隐变量存在的情况下,还成立吗?此外,本例中仅有7个变量,只考虑一阶多元线性回归模型的情况下,我们已经有32种可能的模型,在处理庞大数据库时,我们需要更加自动化的方法帮助我们选择变量。接下来,我们将使用图模型、因果结果模型和do- calculus来帮助我们解答这些问题。
2. 图模型和因果结构模型
2. 图模型和因果结构模型
其实,大家已经在刚才的例子中开始不知不觉地认识了图模型和因果结果模型了。相比于看着所有的变量和公式,画图使得变量的因果关系直观地呈现,这些图叫做Casual graphs(因果图)。他们还有个更通用的名字——有向无环图(DAG, Directed Acyclic Graph)。比如,图14展示了本文例子中的变量因果结构,整张图由顶点(变量)和连接这些顶点的边(表示因果关系)组成。箭头代表因果关系的方向,比如T指向Y,表示T对Y的原因,Y是T的结果。T又可以成为Y的父辈(parent),Y又可以成为T的子辈(child)。然而,这些因果关系并不一定一一对应。例如,T有两个父辈,分别是U1和W;同时,T也有两个子辈,分别是Y和Z。正是因为世间万物互相关联、互相作用,才使得纯粹地估计两个变量之间的因果效应变得十分具有挑战性/有乐趣。通俗地说,探索T对Y因果效应的过程,就是把这两者之间的其他干扰变量(confounder)的作用都剔除的过程。
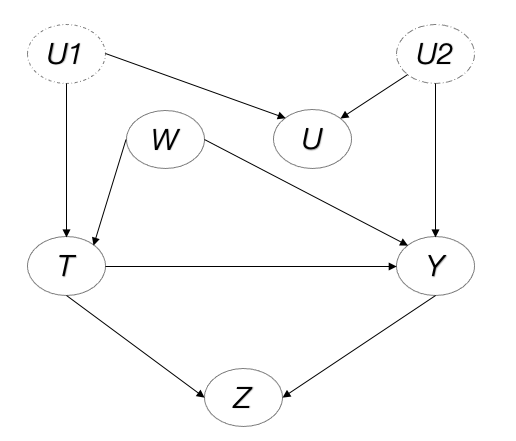
Figure 14 一个因果图的例子
为了用更简洁的语言和符号表示因果图,及其变量间的因果关系,我们规定:
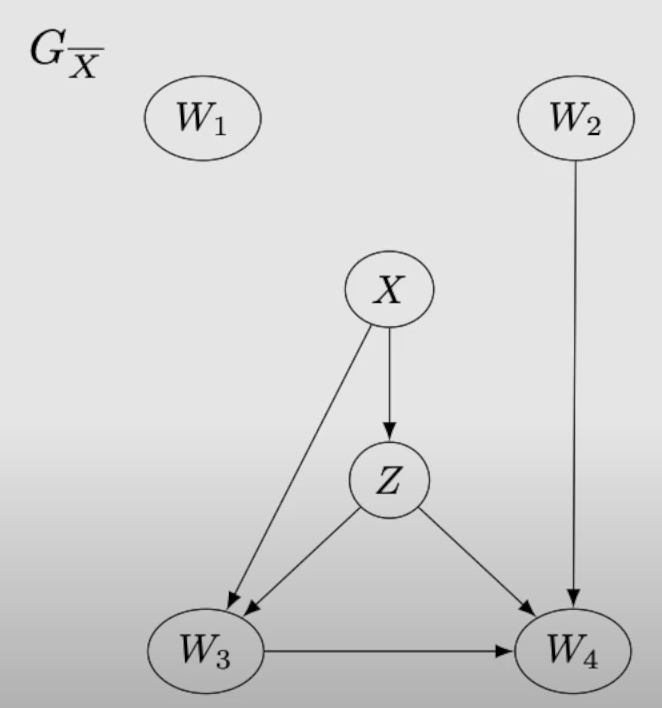
因果图用G表示,一般来说,感兴趣的自变量记做X或者T,因变量可以记作Z或者Y;如图15,我们有了一个因果图G,一对我们感兴趣的X对Z的因果效应,以及其他四个协变量W1-W4。如果我们将图中的所有从X出发的箭头的删除(即删除X的所有子辈),我们将得到的新图记作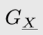 (图16左);类似的,如果将图中所有射向X的箭头删除(即删除X的所有父辈),我们将得到的新图记作
(图16左);类似的,如果将图中所有射向X的箭头删除(即删除X的所有父辈),我们将得到的新图记作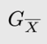 。同理,如果将图中所有射向X的箭头删除,将所有从Z射出的箭头删除,得到的新图记作
。同理,如果将图中所有射向X的箭头删除,将所有从Z射出的箭头删除,得到的新图记作 。
。
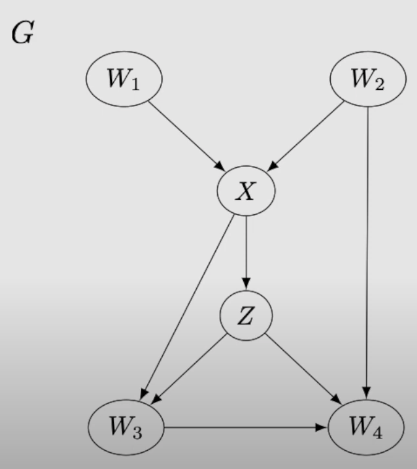
Figure 15 因果图示例
|
|
|
|
Figure 16 因果图
若想要表达两变量A,B之间的因果关系,我们规定使用:
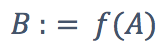
区别于一般的等号,B = A 和A = B是同一个意思;在这里,:= 代表因果关系,即A是B的一个原因。当然,一般情况下,B往往可能有多个原因,并且有很多原因是未知的,或者已知但无法测量的,这时候,我们用U代表无法观测或未知的变量。如下图所示,对应的结构方程为:

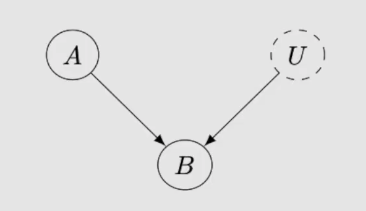
当多个方程组合在一起,可以完整代表一个因果图的信息时,我们便获得了结构因果模型(SCMs, Structural causal model)。如下图,结构因果模型M中有三个结构方程,分别代表了变量B、C、D的因。简言之,结构因果模型可以说是因果图的一种数学表达。

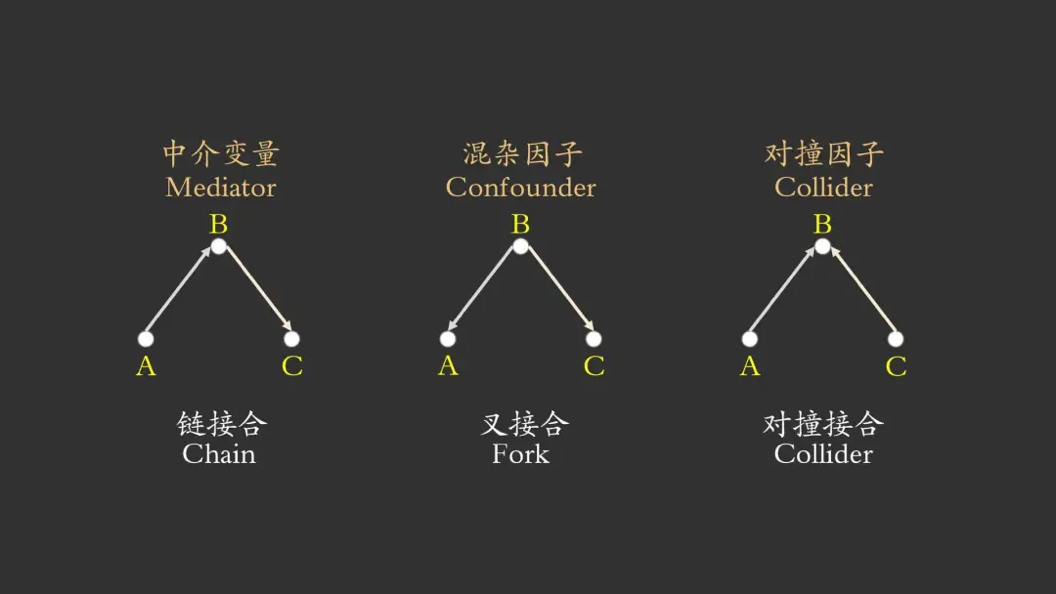
图模型的一个巨大优势在于直观地表示变量的因果关系。集智“因果推断”系列文章里的第一讲有讲到,有向图中的路径,有且仅有三种基础结构:即链接合、叉接合、对撞接合,处于结点的变量分别称为中介变量、混杂因子、对撞因子。
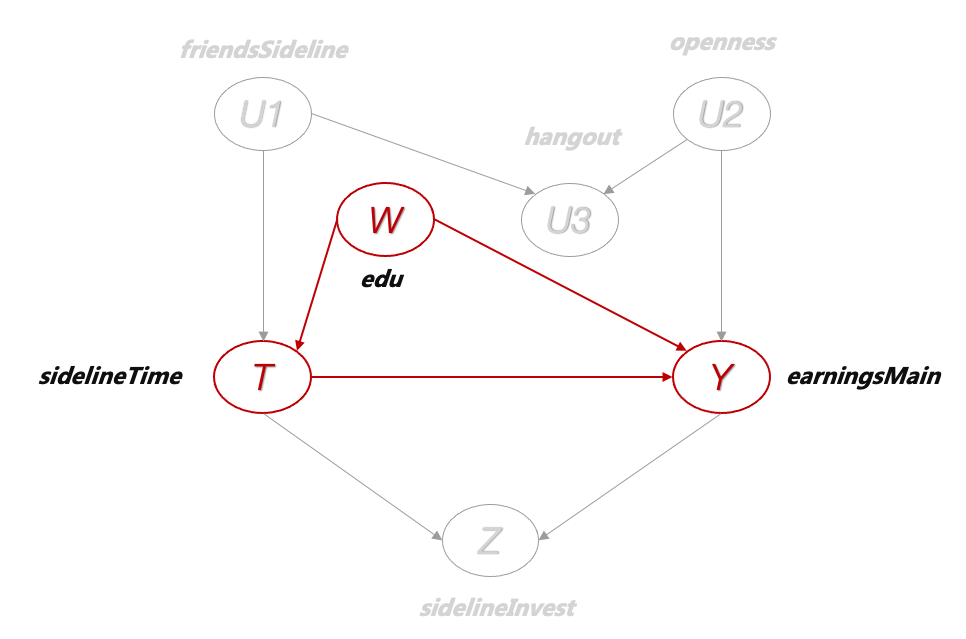
在此基础上,有一些技巧已经被总结出来,帮助大家判断两个变量之间所有路径上的因果信息传递状态。比如说,在本文的例子中,“教育水平”同时是自变量和因变量的父辈,即“教育水平”同时是“副业投入”和“主业收入”的一个原因。
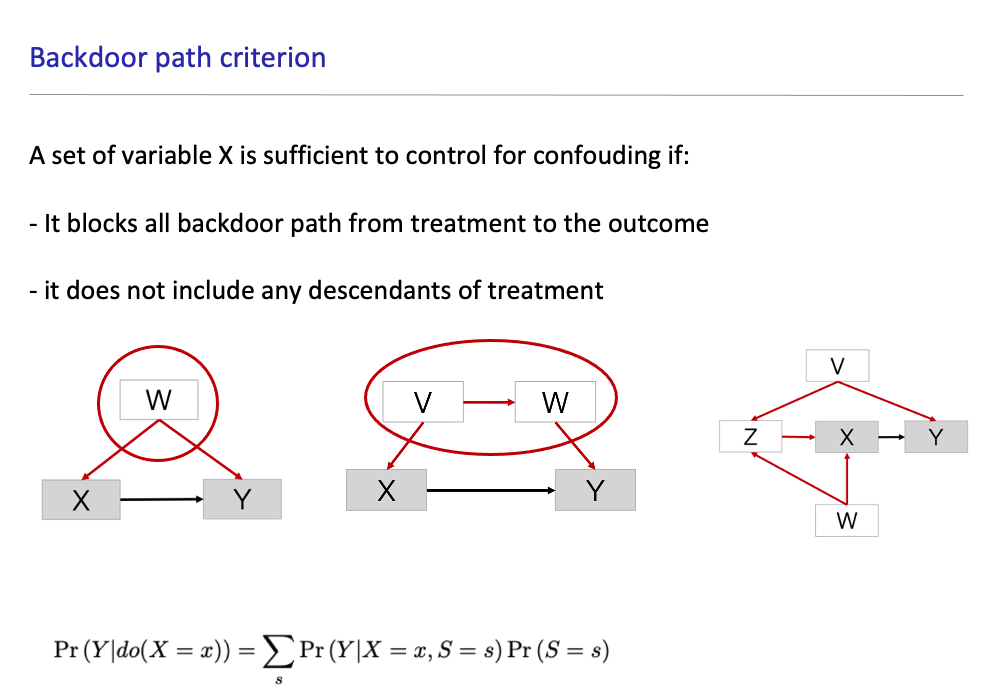
当我们发现图中出现T <– W –> Y这种结构,即“叉接合”结构,我们需要把W的信息加入到模型中。这是因为从T和Y之间的因果信息传递,除了通过T和Y本身外,还通过W这个后门进行传递。所以,为了剔除W传递的因果信息,我们必须要能观测到M,并且将M的信息加入到模型中,才能得到T对Y的因果效应估计。这就是为什么图6的模型1中,因为没有包含“edu”,而导致因果效应估计结果被严重低估的原因。由此衍生的识别策略被称为“后门准则”。也就是说,我们希望能够测量一个或一组变量X满足:(1)堵塞所有X和Y之间的后门;(2)不包括任何X的子辈。比如下图中,W, {V, W}和 {Z,V} {WZV}分别开启了X到Y的后门。左图的情况我们已经非常熟悉,只需要将W的信息加入到模型中即可;中间图,可以加入V,或者W,或者V和W到模型中;右图有两条后门路径,对于XZVY这条路径,加入Z,V或者{Z, V}的信息到模型中;对于XWZVY这套路径,可以加入V, W,或者{Z,V}, {Z,W}的信息。
然而,图中的另一个三角形结构,T Z Y, 是对撞接合,Z作为对撞因子,天然阻隔了T到Y的因果信息传递,因此,如果要将Z作为变量放入模型中,反而会导致有偏估计。这种情况即为d分离(d- separation)。
值得注意的是,当对撞接合和叉接合遇到一起,会产生M结构,如下图,我们知道,对于对撞接合,原本U1和U2就是独立的,但是如果控制了对撞因子U3,可证A和C之间反而会产生条件相关(在已知U3的情况下相关)。对于M结构来说,T-U1-U3-U2-Y这条路径是天然阻隔T和Y的,所以不需要将U1、U2或者U3中的任何一个变量信息提供给模型,如果选择提供信息,除不能仅提供U3的信息(即模型中只包括U3作为协变量,没有U1和U2)这种情况,会导致T和Y之间产生后门,从而无法进行正确的因果效应估计之外,其余组合均可({U1} {U2} {U1, U2}, {U1, U3}, {U2, U3}, {U1,U2, U3})。这也就是为什么图10中一旦仅对hangout进行控制就导致因果效应估计产生偏差,而其他组合都没有问题的原因(图9)。
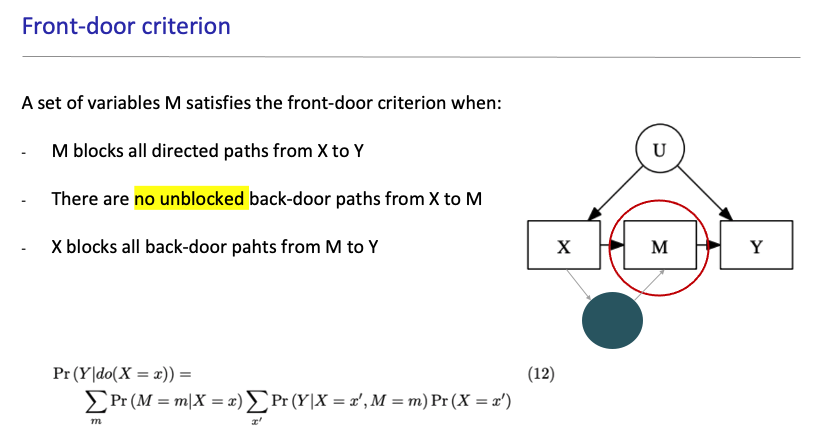
然而,后门法则的一个局限性在于,可能造成后门的变量必须能够被观测到。如果有遗漏的变量(omitted variable),也将会对因果效应估计造成偏差。例如下图中,我们要估计X对Y的因果效应,但是我们知道有一个变量U,同时影响X和Y,但是无法被测量到(比如说大脑某区域的活动影响情绪和行为,但是目前技术手段让我们无法精准测量到该区域的神经活动),此时,链结合为我们提供了两种可能的方案:
第一种与链接合对应的识别策略被称之为前门准则。即存在一组变量M,阻隔所有X到Y的路径,并且从X到M没有任何后门路径,X也阻隔了M到Y的所有后门路径,换句话说,M是X作用于Y的唯一机制和路径。此时,如果我们可以观测到M,并将M的信息提供给模型,我们便依然可以正确对XY之间的因果效应进行估计。但是M的存在往往可遇不可求,世间少有两个变量之间的关系只通过某单一机制进行作用,因此,第二条策略应运而生,并被广泛运用:
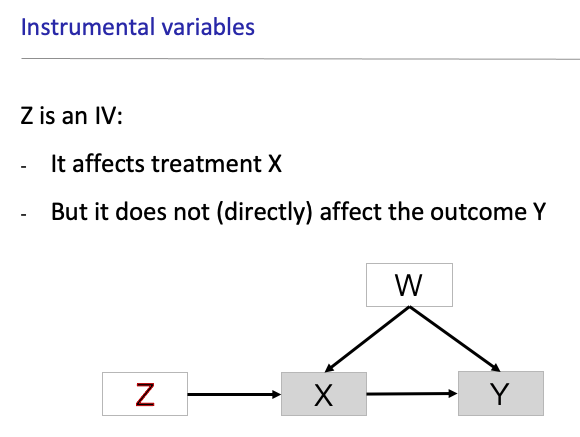
第二种方法,巧妙的利用第三个变量,创造一个链结合。即找到一个变量Z,使其只影响X,并且不直接影响Y,这样就形成了Z->X->Y的链结合。社会科学文献中,抽签是一个非常好的工具变量,如著名的Angrist (1990) 一文中研究参加越战对战后收入的影响,就是用了征兵时的抽签作为工具变量,抽签(Z)只是为了选出参战的士兵,与参战(X)有关,但与其他的事情(战后收入,Y)无关。也就是说,抽签有且只有通过参加越战这一条路径影响战后收入。
3. do-calculus
3. do-calculus
到目前为止,我们通过一个“搞副业”的例子讲解了为什么要使用图模型和因果结构模型来辅助进行因果效应的估计,相信大家已经感受到使用图模型的直观和便捷之处。接下来,我们要很自然的问两个问题,第一,上文提到了三种前门法则、后门法则和工具变量这三种识别策略,但如果前后门准则都不满足的时候,我们还有办法推断因果效应吗?第二,图模型、前门法则、后门法则、工具变量,这些都是通过观察数据进行因果推断的经典方法,比如上文提到的Angrist抽签的文章,已经是1990年的了,近年来,计量经济学和因果推断领域也都有更多新方法涌现,那我们为什么还要习惯和使用另外一套全新的、do- calculus的体系呢?
对第一个问题的回答,答案是“是的!” do-calculus可以实现。准确的来说,Pearl的 do-calculus 可以帮助我们推断任何可被识别(identifiable)的因果关系(因为不是所有的causal quantities 都可被识别)。事实上,Pearl提出了do- calculus的三条规则,所有可被识别的因果关系都可以通过这三条规则被识别。这三条规则的前两条,分别是对前门法则和后门法则的推广(generalization),换言之,前门法则和后门法则分别是前两条规则的特殊、简化情况;此外,由于这三条规则的可编程性、简洁性,与手动跑模型、测试相比,do-calculus是一套可以自动化进行因果推理的方法和体系。从以上两点可以看出do- calculus在因果推断的大领域中具有独特优势。接下来我们首先来看一下什么是do算子,然后来具体看do- calculus的三条规则。
研究因果关系有两种思路,第一种是做实验,满足随机性的情况下,可以得到非常清晰的因果效应关系及其估计;然而,由于有很多事情没法做实验(比如研究吸烟是否致癌,研究人员不能随机要求被试抽烟以追踪其是否会患肺癌),实验的成本很高等原因,很多时候我们往往需要通过使用观察数据(observational data)来模拟实验条件,推断因果关系。如同实验要求满足随机性,使用观察数据,需要通过控制变量等方式来模拟实验条件。在计量经济学的语言体系中,推断因果关系的语言体系是“潜在结果”(potential outcomes)。比如说拿吸烟的A,和平行世界里的不吸烟的A进行比较,观测他们患肺癌的概率是否显著不同。然而,由于我们只能观测到A要么吸烟,要么不吸烟,所以无法观测到的那一种结果,便称为”潜在结果“,要进行因果推断,只能比较吸烟人群和非吸烟人群的肺癌确诊率,但研究人员的目标是通过某种方式,如匹配(matching)来选取不吸烟之前,两组人群的特征在统计学意义上没有显著差别,由此进行推断。
同样的,在do- calculus的体系里,如下图所示,所有的被试要么接受某种Treatment (T = 1),要不不接受(T= 0)。与实验法对应的情况是“intervening”,与观测数据对应的是“conditioning”。do的意思就是,对被试进行干预。同“潜在结果”的思路一致,但现实生活中我们很多时候没有办法干预,所以只能把数据限定在特定的子集上,然后针对这两个子集进行比较。
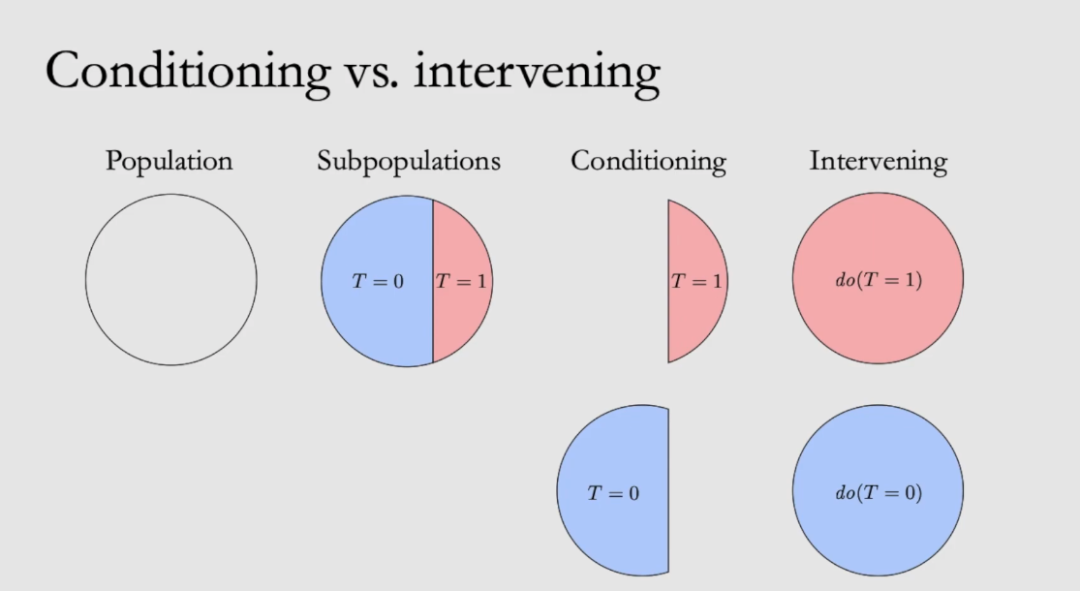
换句话说,同“潜在结果”框架一样,do- calculus也有类似的识别-估计流程,如下图所示:首先,从严格的、理想得实验条件出发,写出如果要无偏估计某两个变量之间的因果关系,需要满足何种实验条件,即Causal Estimand P(Y丨do(T=t), X=x) 。然后,通过Pearl的证明,他发现,在某些情况下,通过干预才能做到的实验条件,可以转化为只用观测数据就能求解。也就是说,这些情况下,一个Causual Estimand(intervening)的问题,可以转化为一个Statistical Estimand(conditioning)的问题来求解,但这个过程需要有对于Causal model的假设,也就是上面所讲的因果图,假设好所有的变量之间的因果关系;最后,只需要将观测的数据代入,即可对因果效应进行估计。

简单来说,do- calculus的过程就是Causal estimand中的所有带do的、不做实验不可知的项,转化为Statistical estimand中不带do的,直接能从观测数据中获得的项。具体怎么转化呢,要根据do- calculus的三种规则:
第一条规则:是否存在可忽略的变量Z?
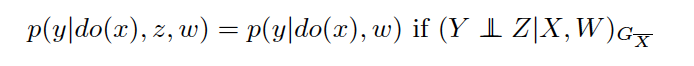
这条规则是说,在满足某种情况下,变量z可以被忽略。具体来说,是指在把所有指向X的箭头都去掉后,在已知X和W的情况下,Y与Z独立。这是不是听着有点耳熟?事实上,把上式所有的do移除之后,我们可以发现,这一条规则其实就是在说d- separation。
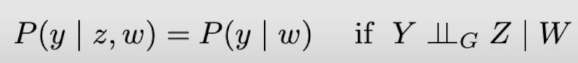
第二条规则:Action/Observation exchange (the back-door criterion)
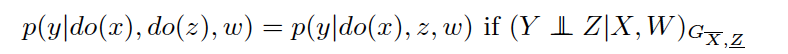
同样的,把所有的do移除之后,我们可以发现,这一条规则其实就是在说backdoor adjustments
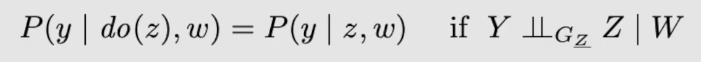
第三条规则:

特例:
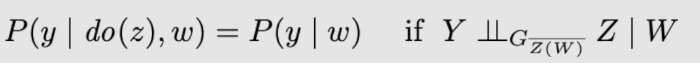
接下来,我们来举例来应用一下这三条规则:
我们的Causal estimand是:
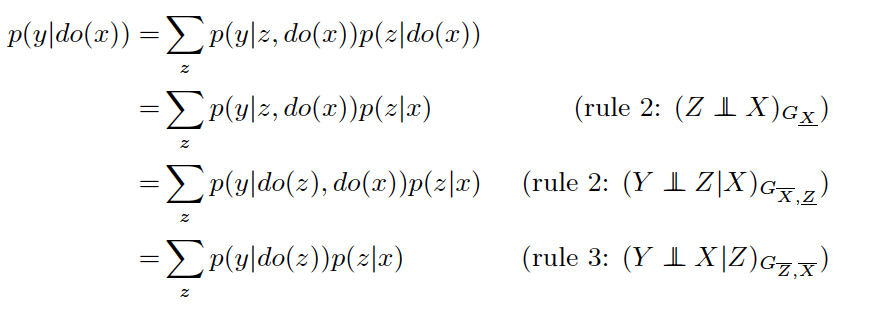
首先我们观察是否有任何可以忽略的变量(比如d- separate中的对撞结构),然后发现没有,所以规则1无法使用。所以我们只能结合规则2和3进行逐步推导,过程如下:

然后,同样的处理思路,我们再在右侧的p(y|do(z))上用一遍:
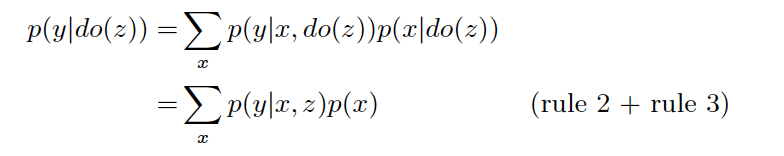
最后,把两边的结果接合在一起,可以得到Statistical Estimand,之后只需要直接带入数据求解即可。
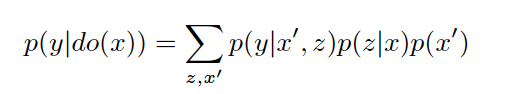
本文主要串讲了Pearl因果识别框架的基础知识,包括图模型、结构因果模型的范式,三种识别策略,以及如何运用do-calculus的三种规则来进行因果识别。那是否存在可被识别的因果关系,但是不能通过do-calculus的以上三条规则来识别呢?幸运的是, do- calculus已经被证明是完整覆盖了所有可识别因果关系的方法(Shpister and Pearl 2006; Huang and Valtorta 2006),即任何可识别的因果关系都可以通过do- calculus的三种规则来识别。
参考文献:
Angrist, J. D. (1990). Lifetime earnings and the Vietnam era draft lottery: evidence from social security administrative records. The American Economic Review, 313-336.
Huang, Y., & Valtorta, M. (2012). Pearl’s calculus of intervention is complete. arXiv preprint arXiv:1206.6831.
Neal,B. (2020). Introduction to Causal Inference from a Machine Learning Perspective. https://www.bradyneal.com/Introduction_to_Causal_Inference-Aug28_2020-Neal.pdf
Pearl, J. (2019). The Seven Tools of Causal Inference with Reflections on Machine Learning, Communications of ACM, 62(3): 54-60, March 2019
Shpitser, I., & Pearl, J. (2012). Identification of conditional interventional distributions. arXiv preprint arXiv:1206.6876.
李奉治. (2020) 因果阶梯与Do-演算:怎样完美地证明吸烟致癌?https://mp.weixin.qq.com/s/SLBXgf8rkJaQwVzZhD_yAQ
因果科学第二季读书会报名中
因果科学第二季读书会报名中
推荐阅读
点击“阅读原文”,即可报名读书会