导语


From the flashes of fireflies to Josephson junctions and power infrastructure, networks of coupled phase oscillators provide a powerful framework to describe synchronization phenomena in many natural and engineered systems. Most real-world networks are under the influence of noisy, random inputs, potentially inhibiting synchronization. While noise is unavoidable, here we show that there exist optimal noise patterns which minimize desynchronizing effects and even enhance order. Specifically, using analytical arguments we show that in the case of a two-oscillator model, there exists a sharp transition from a regime where the optimal synchrony-enhancing noise is perfectly anticorrelated, to one where the optimal noise is correlated. More generally, we then use numerical optimization methods to demonstrate that there exist anticorrelated noise patterns that optimally enhance synchronization in large complex oscillator networks. Our results may have implications in networks such as power grids and neuronal networks, which are subject to significant amounts of correlated input noise.


从萤火虫的闪光，到约瑟夫森结和电力基础设施，耦合相位振子网络提供了一个强有力的框架来描述许多自然和工程系统中的同步现象。大多数现实世界的网络都受到充满噪声的随机输入的影响，可能会抑制同步。虽然噪声是不可避免的，但这项研究表明，存在最优噪声模式能够最小化去同步效应，甚至促进秩序产生。具体而言，作者们用分析论证表明，在双振子模型情况下，存在一个从最优同步增强噪声完全反关联状态，到最优噪声关联状态的急剧转变。更一般地，作者们接着使用数值优化方法证明，存在反关联噪声模式，最优地增强大型复杂振子网络中的同步。该研究结果可能对受大量关联输入噪声影响的网络，如电网和神经元网络等具有重要意义。


研究领域：同步，最优噪声模式，网络拓扑结构

梁金 | 作者

邓一雪 | 编辑



论文题目：

Enhancing Synchronization by Optimal Correlated Noise

论文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.098301




1



在所有尺度的网络和系统中，噪音的出现都是不可避免的，无论是生物学中的神经元，还是机械振子，以及影响电网稳定性的波动输入。非线性相位振子底层网络的同步，是用来理解这种物理和生物网络的一个范例。噪声和波动通常是不受欢迎的，人们做出大量努力来防止它们对网络同步产生有害影响。优化方法已经成功地用来促进有噪声和无噪声情况下的同步，特别是通过调整加权网络拓扑结构。


最近，人们对一种新的可能性很感兴趣——利用噪声增强同步。3月1日发表于PRL上的一项最新研究发现，输入噪声的关联程度可能显著影响其促进或阻止网络同步的能力。基于广泛使用的 Kuramoto 模型，作者们研究了增强振子网络同步的输入噪声关联的最优模式。分析结果表明，在双振子模型情况下，随着总噪声强度增加，最优同步增强噪声会经历从完全反关联到完全关联状态的急剧转变。接着对复杂网络进行数值分析发现，最优输入噪声通常与各种模式反关联，在双振子情况下出现的同步增强噪声的最优模式保留了基本特性。由此发现的最优噪声与网络拓扑结构密切相关。





2




研究首先分析了两个连接的 Kuramoto 振子在一般噪声下的情况。模型由不同固有频率的耦合相振子组成。在弱耦合极限下，可以用 Kuramoto 型方程来模拟相位：



其中 θi(t) 为振子相位，ωi 为固有频率，K 为耦合常数，ηi 为随机白噪声。Kuramoto 序参量 R2 = 1/2 + (1/2)cos(θ1-θ2)。无量纲参数 κ = K/∆ω，无量纲噪声 ζ = (η1 − η2)/∆ω。ς2 是同步的关联有效噪声强度，取决于原始噪声输入 η1,2之间的相关性。

ς2 如何影响同步呢？能够找到一个最优的噪声关联吗？数值模拟结果表明，在转变之前，κ < 1，噪声一般增强同步；而 κ > 1 的情况下，噪声一般降低同步（图1a）。对于固定的 κ，存在一个最优有效噪声 ς2 使同步最大化（图1b）。

图1. 双振子模型中的噪声增强同步和协方差转变。图中为数值方法获得的序参量 ⟨R2⟩。

为了揭示网络拓扑结构与最优噪声之间的关系，作者们对更加复杂的网络进行了数值分析。作为双振子模型最简单的扩展，首先考虑N个振子的周期链。可以发现，与非关联噪声相比（图2a），最优噪声模式能有效增强同步，甚至深入到非线性领域（图2b）。

有趣的是，最优噪声是这样的：具有偶数个振子的链中的相邻一对振子接收反关联输入（图2c,e）。然而，并不总是能让网络中的所有邻居对都接收到完全反关联的输入，从而导致最优噪声的受挫模式。实际上，在奇数振子链中，最优噪声关联的强度会从任何特定的振子 i 处衰减。链拓扑防止任何两个相邻振子接收到完全反关联的噪声（图2d,f）。这种效应在周期性网格中也可以看到。

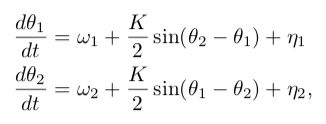
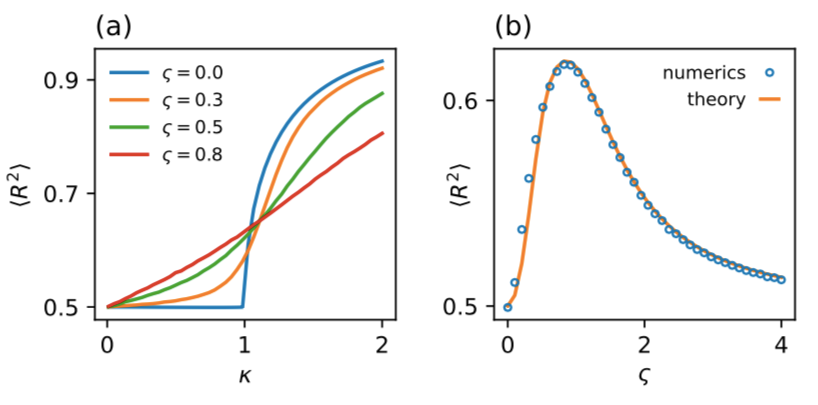
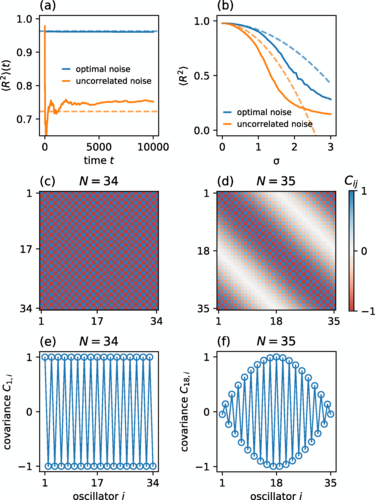
图2. 固定点附近周期振子链的最优噪声模式。（a）对于最优且不相关噪声的 N=54 周期振子链的时间平均序参量；（b）对于最优且不相关噪声的 N=20 周期振子链，数值方法获得的长时间序参量；（c）N=34 偶数周期链的最优协方差矩阵；（d）N=35 奇数周期链的最优协方差矩阵；（e）偶数周期链中第一个振子的最优协方差矩阵 C1,i；（f）相对于奇数周期链中间振子的受挫最优协方差矩阵 C18,i。


有趣的是，在底层网络接近同步转变时，最优噪声本身可能会表现出从局部到全局组织的转变，取决于特定的固有频率（图3），这种转变伴随着序参量的显著增加（图3a）。

图3. N = 12 振子链同步转变附近的最优协方差矩阵。（a）最优噪声显著增强同步转变附近的近似序参量。（b-e）同步转变附近的最优协方差矩阵，不同K值依次对应（a）中的4个红圈。在接近相位漂移区域（小K）时，最优协方差在大尺度有序，然后转变到局部有序。


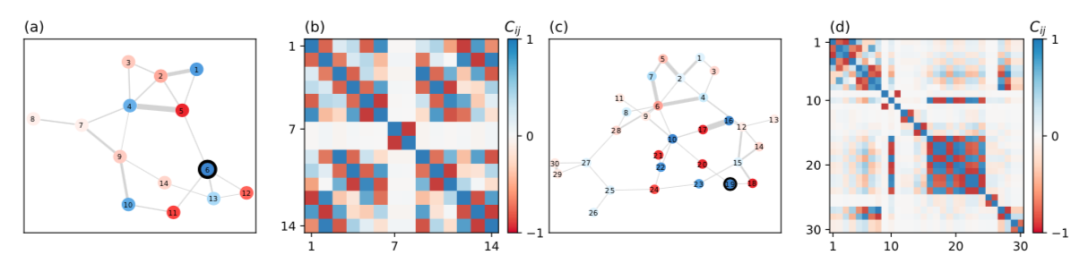
研究者最后考虑了由电网衍生的复杂网络拓扑。这里最优噪声模式显示聚类，其中成组的振子之间近似反关联。聚类之间的关联接近于零（图4），这可能会促进聚类同步（cluster synchronization）。在这些网络中，有一种特殊类型的聚类由一个单一的“悬挂”节点j及其邻居组成。实际电网动力学可以用二阶模型进行建模，该模型显示，网络的最优协方差与惯性具有相关性。

图4. 复杂网络中反关联模式形成聚类。（a） 14-节点的测试电网，节点颜色对应与振子6的关联；（b）（a）中网络的最优协方差矩阵。（c）30-节点的测试电网，节点颜色对应与振子19的关联；（d）（c）中网络的最优协方差矩阵。





3




该研究结果可能对真实网络，如电网和神经元网络具有重要意义。例如，如果根据上述原则布置新的发电厂和线路，可能会加强电网同步，可以估计或通过天气来预测输入噪声的关联性。这项工作为理解和控制复杂系统中的同步开辟了新的途径。


复杂科学最新论文


集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：



推荐阅读



点击“阅读原文”，追踪复杂科学顶刊论文