复杂网络上的自组织与集体行为:从扩散、相变到博弈 | 读书会启动

导语
集智俱乐部联合合肥工业大学物理系教授李明、同济大学副教授张毅超、北京师范大学特聘副研究员史贵元与在读博士生邱仲普、张章共同发起「复杂网络动力学」读书会。本次读书会将探讨:同步相变的临界性、如何普适地刻画多稳态与临界点、如何识别并预测临界转变、如何通过局部干预来调控系统保持或回到期望稳态、爆炸逾渗临界行为的关键特征、不同类型的级联过程对逾渗相变的影响有何异同、高阶相互作用的影响能否等效为若干简单机制的叠加、如何有效地促进人类个体间的合作等问题。
读书会计划从3月7日开始,每周五晚19:30-21:30进行,持续8-10周。诚挚邀请领域内研究者、寻求跨领域融合的研究者加入,共同探讨。
背景介绍
背景介绍
相变与临界现象展现了微观耦合如何驱动宏观秩序的自发涌现;扩散和随机游走过程为研究信息在复杂网络中的传输特性提供了新视角,其简洁的动力学形式直观揭示了网络拓扑结构对动力学行为的影响;而博弈论与网络科学的结合,则更贴近现实系统,使研究者能够深入探索多主体决策与社会互动中的合作、对抗及演化规律。
读书会框架
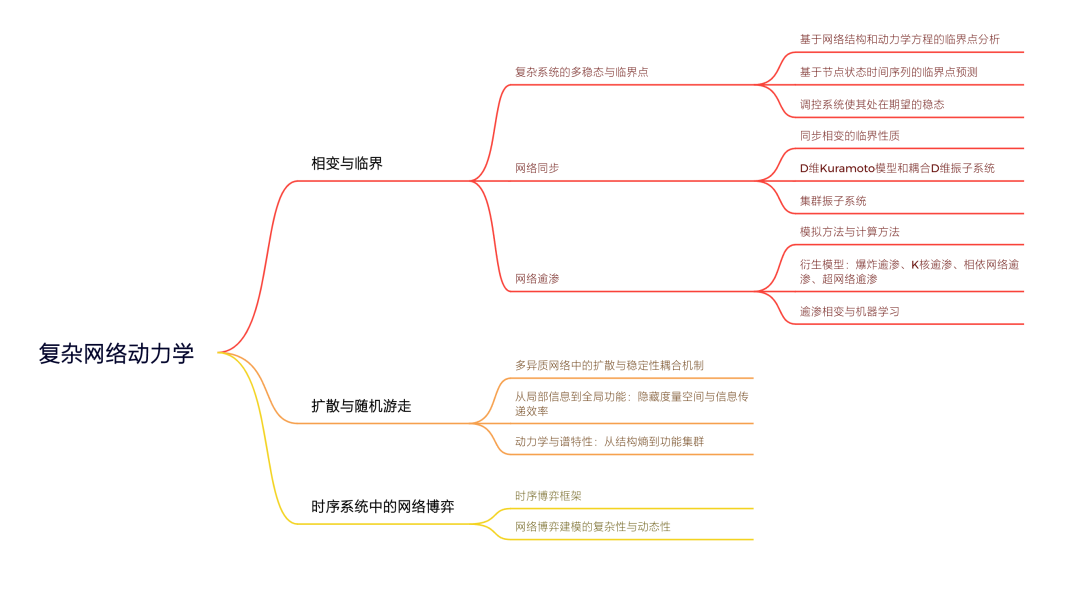
读书会框架
发起人介绍
发起人介绍




报名参与读书会
报名参与读书会
运行模式
报名方式
第一步:扫码填写报名信息。

第二步:填写信息后,付费报名。
如需用支付宝支付,请在PC端进入读书会页面报名支付。
第三步:添加运营负责人微信,获取所有推荐论文资源包,拉入对应主题的读书会社区(微信群)。
加入社区后可以获得的资源
完整权限,包括线上问答、录播回看、资料共享、社群交流、信息同步、共创任务获取积分等。
参与共创任务获取积分,共建学术社区
读书会采用共学共研机制,成员通过内容共创获积分(字幕修改、读书会笔记、论文速递、公众号文章、集智百科、论文解读等共创任务),积分符合条件即可退费。发起人和主讲人同样遵循此机制,无额外金钱激励。
论文清单
论文清单

模块一:相变与临界
1. 复杂系统的多稳态与临界点
重要综述:
[1] Scheffer, Marten, et al. “Anticipating critical transitions.” science 338.6105 (2012): 344-348.
这是临界转变现象的早期综述,系统阐述了识别并预测临界转变的核心思想和方法。
[2] Dakos, Vasilis, et al. “Ecosystem tipping points in an evolving world.” Nature ecology & evolution 3.3 (2019): 355-362.
探讨生态系统在动态环境中可能遭遇的临界点及其应对策略,为理解复杂生态演化提供了重要视角。
[3] Liu, Xueming, et al. “Network resilience.” Physics Reports 971 (2022): 1-108.
基于网络结构和动力学方程的临界点分析:
[4] Gao, Jianxi, Baruch Barzel, and Albert-László Barabási. “Universal resilience patterns in complex networks.” Nature 530.7590 (2016): 307-312.
通过二阶平均场理论(将邻居的邻居视为平均的节点)和动力学方程准线性近似,首次提出高维非线性动力系统降维的通用框架。
[5] Morone, Flaviano, Gino Del Ferraro, and Hernán A. Makse. “The k-core as a predictor of structural collapse in mutualistic ecosystems.” Nature physics 15.1 (2019): 95-102.
通过阶梯函数近似,提出互惠互利生态系统崩溃的临界点可以用网络的最大k-core来解析表示。
[6] Wu, Rui-Jie, et al. “Rigorous criteria for the collapse of nonlinear cooperative networks.” Physical Review Letters 130.9 (2023): 097401.
基于节点状态时间序列的临界点预测:
[7] Scheffer, Marten, et al. “Early-warning signals for critical transitions.” Nature 461.7260 (2009): 53-59.
详细综述了从时间序列统计特征中识别临界转变即将发生早期信号的经典方法。
[8] Liu, Zijia, et al. “Early predictor for the onset of critical transitions in networked dynamical systems.” Physical Review X 14.3 (2024): 031009.
调控系统使其处在期望的稳态:
[9] Sanhedrai, Hillel, et al. “Reviving a failed network through microscopic interventions.” Nature Physics 18.3 (2022): 338-349.
主题推荐语:复杂系统由多个相互作用的单元构成。它们在动态演化中相互协调,从而涌现出集体行为模式。同步是非平衡涌现形式中最简单的一种,涉及通过微观耦合实现系统的宏观状态一致性。以 Kuramoto 模型为代表的耦合随机自然频率振子系统是同步研究领域中的范式性模型。在这一框架下,振子们通过相互作用克服自身自然频率之间的异质性,发生同步相变,使得秩序(order)从无序(disorder)中涌现出来。Kuramoto模型的各种变体可以描述自然和社会中的多种多样的同步现象,其中的若干分支依然各自成为了相对独立的子方向。此外,深刻而新颖的概念方法也层出不穷,如自洽性方程、主稳定函数(Master Stability Function, MSF)、OA 拟设和重整化群等。
主题重点关注:
-
同步与统计物理的交叉领域——同步相变的临界性质;
-
新的内禀自由度——D维Kuramoto模型和耦合D维振子系统;
-
同步与群体运动的交叉领域—— 集群振子模型;
同步相变的临界性质:临界维数和普适类
[1] Daido, H. Lower Critical Dimension for Populations of Oscillators with Randomly Distributed Frequencies: A Renormalization-Group Analysis. Phys. Rev. Lett. 61, 231–234 (1988).
通过重整化群分析揭示了随机分布自然频率振子系统的下临界维数,奠定了理解同步相变临界行为的基石。
[2] Acebrón, J. A., Bonilla, L. L., Pérez Vicente, C. J., Ritort, F. & Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185 (2005).
系统回顾了Kuramoto模型的基本理论与拓展应用,是研究同步现象的经典综述与入门指南。
[3] Hong, H., Chaté, H., Park, H. & Tang, L.-H. Entrainment Transition in Populations of Random Frequency Oscillators. Phys. Rev. Lett. 99, 184101 (2007).
重点讨论了随机频率振子系统中的协频转变(entrainment transition),解析求解了上临界维数,发现存在两种不同的协频转变模式。
[4] Hong, H., Chaté, H., Tang, L.-H. & Park, H. Finite-size scaling, dynamic fluctuations, and hyperscaling relation in the Kuramoto model. Phys. Rev. E 92, 022122 (2015).
通过有限尺寸标度分析求解动力学涨落的临界指数。
[5] Daido, H. Susceptibility of large populations of coupled oscillators. Phys. Rev. E 91, 012925 (2015).
D 维 Kuramoto 模型和耦合 D 维振子系统
[6] Chandra, S., Girvan, M. & Ott, E. Continuous versus Discontinuous Transitions in the $D$-Dimensional Generalized Kuramoto Model: Odd D is Different. Phys. Rev. X 9, 011002 (2019).
系统性地研究了D-维广义Kuramoto模型在奇数D-维与偶数D-维下的同步转变方式,揭示了序参量维数奇偶性对于系统同步行为的显著差异。
[7] Dai, X. et al. Discontinuous Transitions and Rhythmic States in the D-Dimensional Kuramoto Model Induced by a Positive Feedback with the Global Order Parameter. Phys. Rev. Lett. 125, 194101 (2020).
在全局序参量上引入正反馈,发现了D-维广义Kuramoto模型中的新的节律状态,区别于传统的奇美拉态。
[8] Kovalenko, K. et al. Contrarians Synchronize beyond the Limit of Pairwise Interactions. Phys. Rev. Lett. 127, 258301 (2021).
探讨了“唱反调者”(contrarians)在多体相互作用情况下的同步现象,突破了传统二体相互作用的限制。
[9] Dai, X. et al. D-dimensional oscillators in simplicial structures: Odd and even dimensions display different synchronization scenarios. Chaos, Solitons & Fractals 146, 110888 (2021).
面向单纯形结构中的高维振子,揭示了奇数和偶数维系统在同步动力学上展现的不同场景与机制。
[10] Zou, W., He, S., Senthilkumar, D. V. & Kurths, J. Solvable Dynamics of Coupled High-Dimensional Generalized Limit-Cycle Oscillators. Phys. Rev. Lett. 130, 107202 (2023).
集群振子模型
[11] O’Keeffe, K. P., Hong, H. & Strogatz, S. H. Oscillators that sync and swarm. Nat Commun 8, 1504 (2017).
提出集群振子模型“Swarmalator”概念,将空间集群与相位同步结合,开辟了时空协同自组织研究的新领域。
[12] Yoon, S., O’Keeffe, K. P., Mendes, J. F. F. & Goltsev, A. V. Sync and Swarm: Solvable Model of Nonidentical Swarmalators. Phys. Rev. Lett. 129, 208002 (2022).
针对非同质性Swarmalator系统建立可解析模型,深入揭示群体动力学与个体异质性之间的相互影响。
[13] Anwar, M. S., Sar, G. K., Perc, M. & Ghosh, D. Collective dynamics of swarmalators with higher-order interactions. Commun Phys 7, 1–11 (2024).
主题重点关注:
-
爆炸逾渗临界行为的关键特征?
-
不同类型的级联过程对逾渗相变的影响有何异同?
-
高阶相互作用的影响能否等效为若干简单机制的叠加?
-
爆炸逾渗(Explosive Percolation),通过引入集团生长的异质机制,产生了丰富的临界现象[Science 323, 1453 (2009)]。最初被认为是不连续相变[Phys. Rev. Lett. 103, 255701 (2009); Phys. Rev. Lett. 103, 045701 (2009); Phys. Rev. Lett. 103, 135702 (2009); Phys. Rev. Lett. 103, 168701 (2009); Phys. Rev. E 82, 051105 (2010); Phys. Rev. E 81, 036110 (2010); Phys. Rev. Lett. 104, 195702 (2010); Phys. Rev. Lett. 107, 275703 (2011).],后被证明为连续相变[Science 333, 322 (2011); Phys. Rev. Lett. 105, 255701 (2010); Phys. Rev. E 84, 020101(R) (2011)],进而大量数值结果显示其有异常的有限尺度标度行为[Phys. Rev. Lett. 106, 225701 (2011); Nat. Phys. 11, 531 (2015)],而近期被证实在基于事件的系综下,仍服从标准的有限尺度标度理论[Phys. Rev. Lett. 130, 147101 (2023); Phys. Rev. Research. 6, 033319 (2024)];
-
k核逾渗(k-core Percolation),关注更稠密或紧致的连通集团的涌现。临界现象的讨论(混合相变)[Phys. Rev. Lett. 96 (2006) 040601; Phys. Rev. E 94 (2016) 062307; Phys. Rev. E 78 (2008) 022101; Phys. Rev. Lett. 122 (2019) 108301; New J. Phys. 26, 013006 (2024); Nat. Comm. 15 (2024) 5850]; 连续与不连续相变的交跨行为[Phys. Rev. Lett. 107 (2011) 175703; Phys. Rev. E 83 (2011) 051134; Phys. Rev. E 87 (2013) 022134];k核在复杂网络上应用的综述[Phys. Rep. 832 (2019) 1-32]
-
相依网络逾渗(Percolation on interdependent Networks),强调多层或互联网络之间的耦合失效对整体连通性的影响。模型的提出[Nature 464 (2010) 1025; Phys. Rev. Lett. 105 (2010) 048701];更简单的解析方法 [Europhys. Lett. 97 (2012) 16006];混合相变的讨论[Phys. Rev. Lett. 109 (2012) 248701; Phys. Rev. Lett. 129, 268301,2022]
-
超网络逾渗(Percolation on hypergraphs),超网络逾渗关注具有高阶相互作用的系统。[Phys. Rev. E 104, (2021) 034306, Phys. Rev. E 109, (2024)014306] 给出了单个网络和多个网络的逾渗理论。然而,超图中的超边往往包含多个节点,不同于简单网络中一条边中一个节点的删除必然会导致这条边被删除,[Chaos, Solitons & Fractals,173(2023), 113645] 提出了 (k,q)-core分解的方法来找到由至少连接k条基数大于等于m的超边的节点所组成的巨分支,[Nature Communications,14 (2023), 6223] 验证了(k,q)-core在超图中的高传播能力和局域性。此外,在渗流过程中,节点还可能对超边具有不同的作用机制,一种作用机制是一个或部分节点 [Chaos, Solitons & Fractals, 173, (2023), 113746] 的就会导致超边中的剩余节点的删除,而另一种机制是一个或部分节点的删除会导致超边的解体,而其余节点并不会被删除 [Chaos, Solitons & Fractals, 177, (2023), 114246; Chaos 34, (2024)043148]。另外,[Phys. Rev. Lett. 132, 087401 (2024)]研究了超图中由高阶连接所形成的高阶分支(higher-order components) 对超图上高阶传染动力学的爆发模式的影响。(此条由杭州师范大学刘润然教授整理)
书籍或综述:
[1] Stauffer D, Aharony A. Introduction to percolation theory[M]. Taylor & Francis, 2018.
偏向基础与经典,是系统、入门的书籍,从基本模型到临界理论都有清晰的讲述。
[2] Li M, Liu R R, Lü L, et al. Percolation on complex networks: Theory and application[J]. Physics Reports, 2021, 907: 1-68.
逾渗相变与机器学习:
说明:以下研究以经典系统为研究对象,而非网络系统,供参考。
[3] Zhang W, Liu J, Wei T C. Machine learning of phase transitions in the percolation and XY models[J]. Physical Review E, 2019, 99(3): 032142.
采用机器学习识别逾渗与XY模型的临界点,展示人工智能在复杂相变问题上的可行性与高精度潜能,适合探索多模型通用性研究。
[4] Oh S M, Choi K, Kahng B. Machine learning approach to percolation transitions: global information[J]. Journal of Statistical Mechanics: Theory and Experiment, 2023, 2023(8): 083210.
从全局信息出发,用机器学习方法揭示逾渗相变特征,为大规模网络或复杂系统中关键结构检测提供全局性视角。
[5] Kamrava S, Tahmasebi P, Sahimi M, et al. Phase transitions, percolation, fracture of materials, and deep learning[J]. Physical Review E, 2020, 102(1): 011001.
将深度学习融入相变、逾渗与材料断裂研究,探索多尺度复杂性下的预测与模拟,对材料工程与地质分析具有重要参考价值。
[6] Shen J, Liu F, Chen S, et al. Transfer learning of phase transitions in percolation and directed percolation[J]. Physical Review E, 2022, 105(6): 064139.
将深度学习融入相变、逾渗与材料断裂研究,探索多尺度复杂性下的预测与模拟,对材料工程与地质分析具有重要参考价值。
[7] Shen J, Li W, Deng S, et al. Supervised and unsupervised learning of directed percolation[J]. Physical Review E, 2021, 103(5): 052140.
结合有监督与无监督学习手段,深挖定向逾渗的临界行为,为基于数据驱动的非平衡相变探索提供了新思路与实用方法。
[8] Zhang J, Zhang B, Xu J, et al. Machine learning for percolation utilizing auxiliary Ising variables [J]. Physical Review E, 2022, 105(2): 024144.
模块二:扩散与随机游走
主题重点关注:
-
多层异质网络中的扩散与稳定性耦合机制
-
从局部信息到全局功能:隐藏度量空间与信息传递效率
-
动力学与谱特性:从结构熵到功能集群
[1] Snijders, T. A. The statistical evaluation of social network dynamics. Sociological methodology 31,361–395 (2001). https://www.jstor.org/stable/3097281
在社会网络分析中,为理解网络随时间的动态变化提供了可估计、可模拟的统计框架;能够同时考虑网络效应(如互惠、传递性等)和外部协变量(个体或二元性特征)。
[2] Tyson, J. J., Chen, K. & Novak, B. Network dynamics and cell physiology. Nature reviews Molecular cell biology 2, 908–916 (2001). https://pubmed.ncbi.nlm.nih.gov/11733770/
强调“动力学系统”的建模方法对细胞网络的理解具有重要意义;为生物领域中将网络结构与动力学过程相结合的研究开辟了道路。
[3] Guimer`a, R., D´ıaz-Guilera, A., Vega-Redondo, F., Cabrales, A. & Arenas, A. Optimal network topologies for local search with congestion. Physical Review Letters 89 (2002). https://doi.org/10.1103/physrevlett.89.248701.
揭示在并行搜索负载较低时,星状网络最优;但当搜索量较大时,均匀-各向同性网络拓扑则更具优势。对互联网、交通以及社会网络中的搜索与拥塞问题有启示意义。
[4] Chavez, M., Hwang, D.-U., Amann, A., Hentschel, H. G. E. & Boccaletti, S. Synchronization is enhanced in weighted complex networks. Physical Review Letters 94 (2005). https://doi.org/10.1103/physrevlett.94.218701.
展示了网络结构(尤其是加权方式的精巧设计)对同步过程的促进效应,为研究多振子或多代理的同步现象提供了新的思路。
[5] Arenas, A., D´ıaz-Guilera, A. & P´erez-Vicente, C. J. Synchronization reveals topological scales in complex networks. Physical Review Letters 96 (2006). https://doi.org/10.1103/physrevlett.96.114102.
在理论与数值实验层面,将同步过程与谱图分析(比如拉普拉斯矩阵谱)紧密联系起来,揭示模块化或多层次结构在网络动力学演化中的重要性。
[6] Bogu˜n´a, M., Krioukov, D. & Claffy, K. C. Navigability of complex networks. Nature Physics 5, 74–80(2008). https://doi.org/10.1038/nphys1130.
证明了自然界和人造系统中的许多网络之所以能够在仅使用局部信息的条件下实现高效路由,是因为它们具有内在的几何特征。为理解随机行走、贪心路由与度量几何在网络中的统一机制奠定了基础。
[7] G´omez-Garde˜nes, J., Campillo, M., Flor´ıa, L. M. & Moreno, Y. Dynamical organization of cooperation in complex topologies. Physical Review Letters 98 (2007). https://doi.org/10.1103/physrevlett.98.108103.
定量展示了网络节点度分布对合作形成和演化的影响:在无标度网络中,高度节点(hub)倾向于成为合作者并形成单一大型合作集群。
[8] Barzel, B. & Barab´asi, A.-L. Universality in network dynamics. Nature physics 9, 673–681 (2013). https://www.nature.com/articles/nphys2741
提供了一个涵盖多种连续动力学过程的统一框架;通过数值验证及对生物、社会系统的实测数据分析,显示出该方法可识别不同网络动力学的普适性特征。
[9] Domenico, M. D. & Biamonte, J. Spectral entropies as information-theoretic tools for complex network comparison. Physical Review X 6 (2016). https://doi.org/10.1103/physrevx.6.041062.
从网络的拉普拉斯谱或相应算子谱出发,通过信息熵来衡量网络的结构差异;可应用于网络模型参数估计、模型选择以及多层网络的聚类分析等。
[10] Harush, U. & Barzel, B. Dynamic patterns of information flow in complex networks. Nature Communications 8 (2017). https://doi.org/10.1038/s41467-017-01916-3.
发现对于一类常见的非线性耦合系统,信息流并非总是经过中心节点(hub),甚至会出现“信息绕开中心”而通过外围路径流动的情形;对于理解网络中的真实信息传播至关重要。
[11] Domenico, M. D. Diffusion geometry unravels the emergence of functional clusters in collective phenomena. Physical Review Letters 118 (2017). https://doi.org/10.1103/physrevlett.118.168301.
提供了一个将功能性分区(functional clusters)与“扩散几何”(diffusion geometry)相结合的统一视角,有助于理解许多生物、社会、工程网络中的多尺度功能划分。
[12] Meena, C. et al. Emergent stability in complex network dynamics. Nature Physics 19, 1033–1042(2023). https://doi.org/10.1038/s41567-023-02020-8.
模块三:时序系统中的网络博弈
主题重点关注:
-
网络博弈建模的复杂性与动态性,从复杂的多方交互、动态网络环境到高维策略空间;
-
人工智能(AI)在网络博弈中的应用,包括智能体的策略、多智能体系统优化;
[1] M. A. Nowak and R. M. May, “Evolutionary games and spatial chaos,” Nature, vol. 359, pp. 826–829, 1992.
构建了网络博弈框架,首次提出网络结构会对个体间合作产生显著的影响。
[2] G. Szabo and G. Fáth, “Evolutionary games on graphs,” Phys. Rep., vol. 446, pp. 97–216, 2007.
系统地从动力学、网络结构、博弈种类等多个角度介绍网络博弈的相关基础。
[3] D. G. Rand, S. Arbesman, and N. A. Christakis, “Dynamic social networks promote cooperation in experiments with humans,” Proc. Nat. Acad. Sci. USA, vol. 108, pp. 19193–19198, 2011.
设计了实证实验,证明了网络的高动态性可以显著提高人类群体合作水平。
[4] W. Press and F. Dyson, “Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent,” Proc. Nat. Acad. Sci. USA, vol. 109, pp. 10409–10413, 2012.
2010年以后,重复博弈理论研究的代表性成果,证明了基于特定策略博弈一方可以限制另一方的收益。
[5] Y. Zhang, G. Chen, J. Guan, Z. Zhang, S. Zhou, “Unfavorable individuals in social gaming networks,” Scientific Reports, vol. 5, p. 17481, 2015.
构建了分治博弈框架,分析个体的度对其博弈收益波动范围的影响。
[6] C. Shen, C. Chu, L. Shi, M. Perc, and Z. Wang, “Aspiration-based coevolution of link weight promotes cooperation in the spatial prisoner’s dilemma game,” Roy. Soc. Open Sci., vol. 5, 2018, Art. no. 180199.
构建了边权与博弈共演化的系统,揭示收益预期对于群体合作水平演化的影响。
[7] D. Melamed, A. Harrell, and B. Simpson, “Cooperation, clustering, and assortative mixing in dynamic networks,” Proc. Natl. Acad. Sci. U.S.A., vol. 115, no. 5, pp. 951–956, Jan. 2018.
揭示初始拓扑结构是否具有较高的群聚性对于动态网络中的合作水平没有影响,但对静态网络合作水平的影响显著。此外,声誉会影响合作伙伴的选择但不影响合作水平。分治或统一决策对于动态网络中合作水平的影响不大,但对静态网络合作水平的影响显著。
[8] M. Perc, J. J. Jordan, D. G. Rand, Z. Wang, S. Boccaletti, A. Szolnoki, “Statistical physics of human cooperation,” Physics Reports, vol. 687, pp. 1-51, 2017.
从方法论的层面介绍研究人类合作的各种统计物理方法。
[9] Y. Zhang, G. Wen, G. Chen, J. Wang, M. Xiong, J. Guan, and S. Zhou, “Gaming temporal networks,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 66, no. 4, pp. 672–676, 2018.
在分治博弈的框架下揭示人类协作阵发性源于理性互动,从时间的角度重新认识分治博弈的动力学特征。
[10] Y. Zhang, J. Wang, G. Wen, J. Guan, S. Zhou, G. Chen, K. Chatterjee, and M. Perc, “Limitation of Time Promotes Cooperation in Structured Collaboration Systems,” IEEE Transactions on Network Science and Engineering, vol. 12, no. 1, pp. 4-12, 2025.
推荐阅读
1. 探索网络动力学系列课程
6. Barabási算法+Physics Reports精选,网络科学综述10年Top10 | 妙算复杂

点击“阅读原文”,报名读书会










