三体问题:三百年探索历程 | 集智百科


在物理学和经典力学领域中,三体问题 Three-body problem是根据牛顿运动定律和牛顿万有引力定律按照三点处质量体的初始位置和速度(或动量)求出它们随后的运动的问题。三体是N体问题中的一个特例。与双体问题不同的是,三体问题不存在一般的闭式解,因为产生的动力系统对于大多数初始条件来说是混沌的,所以一般需要数值方法求解。
历史上看,第一个被拓展研究的特定三体问题是月球、地球和太阳构成的“三体”问题。从现代意义上讲,拓展的三体问题可以是经典力学或量子力学中模拟三个粒子运动的任何问题。
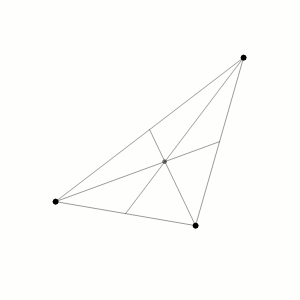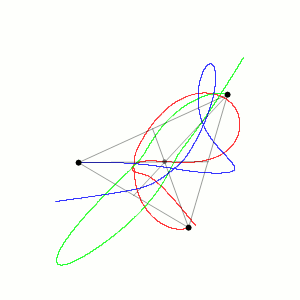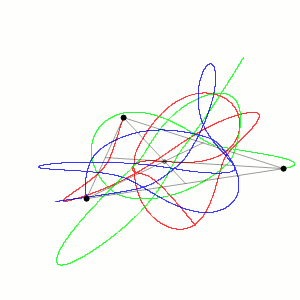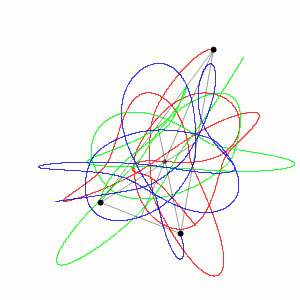
位于不等边三角形顶点且初始速度为零的三个相同物体的近似轨迹。可以看出,在质量中心,根据动量守恒定律,保持不变。
数学描述
三体的数学表达式可以用三个质量为mi的相互作用的物体的矢量位置ri=(xi,yi,zi)的牛顿运动方程来表示:
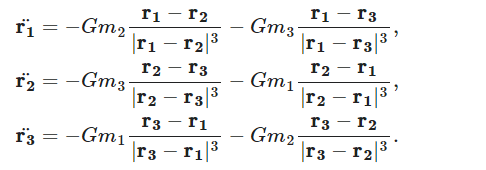
其中G为万有引力常数。这是一组9个二阶微分方程构成的方程组。这个问题也可以用哈密顿形式等价表示,此时可以用一组18个一阶微分方程来描述,这些方程分别对应于位置ri和动量pi的一个分量:

受限制的三题问题
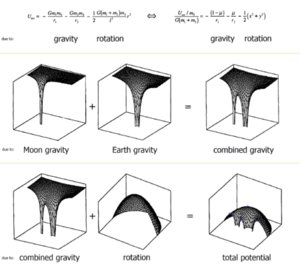
圆形受限三体问题是在太阳系中发现的椭圆轨道的有效近似,这可以看作是由于两个主要天体的重力以及它们旋转(科里奥利)产生的离心效应而产生的势的组合效果是动态的,未显示)。然后可以将拉格朗日点视为合成表面上梯度为零的五个位置(显示为蓝线),表明力在那里处于平衡状态。
在受限制的三体问题中,一个质量可忽略不计的天体(“小行星”)在两个质量巨大的天体的影响下运动。由于质量可忽略不计,小行星对这两个质量巨大的天体所施加的力可忽略不计,因此可以可以用两个物体的运动来描述,对该系统进行分析。通常这种两体运动被认为是由围绕质心的圆形轨道组成的,并且假定小行星在圆形轨道所定义的平面内运动。
受限制的三体问题比完全的三体问题更容易从理论上分析。它也具有实际意义,因为它准确地描述了许多现实世界的问题,其中最重要的例子是地球-月亮-太阳的系统,这也是在三体问题的历史发展中有重要地位的一个典型。
在数学的表述上,设m1,2为两个大质量天体的质量,二维平面坐标(xi,yi)和(x2,y2)分别为小行星的坐标。简单起见,选择的单位应该要确保两大质量天体的距离和重力常数都等于1。则小行星的运动可以用公式描述为:
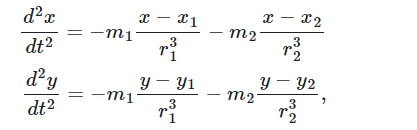
其中,
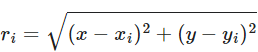
在这种形式下,运动方程通过坐标具有明确的时间依赖性xi(t),yi(t)。但可以通过转换为旋转参考系来消除这种时间相关性,从而简化了后续的分析。
求解
由简单的代数表达式和积分给出的三体没有一般的解析解。此外,除特殊情况,三个物体的运动一般是不重复的。
另一方面,1912年芬兰数学家Karl Fritiof Sundman 证明了三体问题存在一个 t1/3幂次方的级数解。除了对应于角动量为零的初始条件外,这个级数对所有实数t都收敛。
证明这个结果的一个重要问题是,该序列的收敛半径是由到最近奇点的距离决定的。因此,有必要研究三体问题的可能奇点。三体问题中唯一的奇点是二元碰撞(两个粒子在瞬间的碰撞)和三元碰撞(三个粒子在瞬间的碰撞),下面会进行简单的讨论。
无论是二元的还是三元的(事实上是任何数目) 碰撞都不太可能发生,因为已经证明它们对应于测度为零的一组初始条件。然而,没有已知的标准被放在初始状态,以对相应的解避免碰撞。因此,**Sundman**的求解方法包括以下步骤:
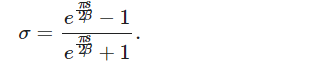
上述即为完整的Sundman定律的证明。
但不幸运的是,对应的级数收敛得非常慢。也就是说,为了获得一定精度的值需要很多级数项,这样的解法并没有什么实际用途。的确,在1930年,大卫·贝洛里奇 David Beloriszky计算出,如果将Sundman级数用于天文观测,则计算将至少涉及108000000项。
特殊的求解方法
1767年, 莱昂哈德·欧拉 Leonhard Euler提出了三个周期解系列,其中三个质量在每个瞬间共线。
1772年,拉格朗日 Lagrange找到了一系列解,其中三个质量在每个瞬间形成一个等边三角形。这些解决方案与欧拉的共线解一起构成了三体问题的中心配置。这些解决方案对于任何质量比均有效,并且质量沿开普勒椭圆形运动。这四个族是唯一有明确解析公式的已知解决方案。在圆形受限三体问题的特殊情况下,这些解决方案在与原边一起旋转的框架中观察时,变为称为L1, L2, L3, L4和L5,并且叫做拉格朗日点,其中L3, L4是拉格朗日的对称解的实例。
在1892年至1899年的工作中,亨利·波因加 Henri Poincaré建立了无穷有限三体问题的周期解,以及将这些解法继续推广到一般三体问题的技巧。
1893年,迈塞尔提出了现在所说的毕达哥拉斯三体问题:将比例为3:4:5的三个质量置于3:4:5直角三角形的顶点处。布鲁 Burrau在1913年进一步研究了这个问题。1967年,维克多·塞贝赫利 Victor Szebehely和弗雷德里克·彼得斯 C. Frederick Peters利用数值积分理论建立了这个问题的最终逃逸模型,同时找到了附近的周期解。
20世纪70年代,米歇尔·赫农 Michel Hénon和 罗杰A.布鲁克 Roger A. Broucke各自找到了一套解决方案,这些解决方案构成了同一系列解决方案的一部分: 布鲁克-赫农-哈德吉德梅特里奥 Broucke–Henon–Hadjidemetriou族。在这个家族中,这三个物体都具有相同的质量,可以表现出逆行和直行两种形式。在布鲁克的一些解中,两个物体遵循同样的路径。
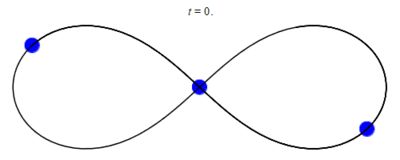
三体问题的图 8 解在单个周期 T ≃ 6.3259 上的动画。
1993年,圣塔菲研究所的物理学家克里斯摩尔 Cris Moore提出了一种零角动量解,该解适用于三个相等质量围绕一个八字形运动。这种方法在2000年由数学家阿兰·契纳 Alain Chenciner和理查德·蒙哥马利 Richard Montgomery证明。在数值上证明了该解对于质量和轨道参数的小扰动是稳定的,这增加了在物理宇宙中可以观察到这种轨道的可能性。但有人认为不太可能发生这种情况,因为稳定性的范围小。在数值上证明了该解对于质量和轨道参数的小扰动是稳定的,这增加了在物理宇宙中可以观察到这种轨道的可能性。但是,由于稳定性的范围小,因此不太可能发生这种情况。例如,二元-二元散射事件导标号-8轨道的概率估计为1%的一小部分。
2013年,贝尔格莱德物理研究所的物理学家 米洛万·乌瓦科夫 Milovan uvakov 和 维利科·德米特拉·伊诺维 Veljko dmitra inovi 发现了等质量零角动量三体问题的13种新的解族。
2015年,物理学家 安娜·胡多马尔 Ana Hudomal 发现了14种等质量零角动量三体问题的新解族。
2017年,研究人员 李晓明 Xiaoming Li 和 廖世俊 Shijun Liao发现了669个等质量零角动量三体问题的新周期轨道。2018年,不等质量的零动量系统又增加了1223个新解。
2018年,李晓明和廖世俊提出了234个不等质量“自由落体”三体问题的解。三体问题的自由落体公式从所有三个静止的物体开始。正因为如此,质量在一个自由落体配置不在一个闭合的“循环”轨道上运行,而是沿着一个开放的“轨道”向前和向后运行。
数值方法
尽管高精度需要大量的CPU时间,但是通过计算机可以使用数值积分可以得到问题的任意高精度解。在2019年,布林 Breen等人。提出了一种快速的神经网络求解器,使用数字积分器对其进行训练。
历史
传统意义上的三个物体的引力问题可以追溯到1687年,当时 艾萨克·牛顿 Isaac Newton 发表了他的《自然哲学的数学原理》。在《原理》第一卷的第66号提案及其22个推论中,牛顿首次定义和研究了三个受相互扰动的重力吸引影响的巨大物体的运动问题。在第三册的第25至35条命题中,牛顿也迈出了第一步,将他的66号提案的结果应用到月球理论中,即月球在地球和太阳的引力影响下的运动。
亚美利哥·韦斯普奇 Amerigo Vespucci和随后的 伽利略·伽利雷 Galileo Galilei提出了三体问题; 1499年,韦斯普奇 Vespucci利用对月球位置的了解来确定自己在巴西的位置。因为这种方法适用于导航,特别是在海上确定经度,1720年代该方法变得非常技术实用。事实上确定经度的问题被 约翰·哈里森 John Harrison发明的航海经线仪所解决。但是,由于太阳和行星对月球绕地球运动的干扰作用,月球理论的准确性很低。
建立了长期竞争关系的 让·勒朗·达朗贝尔 Jean le Rond d’Alembert 和 亚历克西斯·克莱奥特 Alexis Clairaut都试图以某种普遍性来分析该问题。他们于1747年向皇家科学研究院提交了他们的第一批竞争分析。在1740年代的巴黎,“三体问题”(法语:Problèmedes trois Corps)这个名字开始被普遍使用,与他们的研究有关。让·勒朗·达朗贝尔 Jean le Rond d’Alembert于1761年发布的文章表明该名称最早于1747年使用。
2019年,Breen等人宣布了一种用于三体问题的快速神经网络求解器,使用数值积分器进行训练。
其他涉及三体的问题
三体问题这个术语有时用在更一般的意义上来指涉及三个物体相互作用的任何物理问题。
氦原子是经典力学中引力三体问题的量子力学模拟,其中一个氦原子核和两个电子会产生反平方库仑相互作用。就像引力三体问题一样,氦原子的三体问题没有精确解。
然而,在经典力学和量子力学中,除了平方反力外,还存在着一些非平凡相互作用规律,这些规律可以得到精确的解析解。有一种模型是由谐波吸引和排斥反立方体力的组合而成的。该模型被认为是非平凡的,因为它与一组包含奇异性的非线性微分方程组相关联(例如,与单独的谐波相互作用相比,该关联能够得到易于求解的线性微分方程组)。在这两种情况下,三体问题类似于具有库仑相互作用的(无法解释的)模型,因此,有人提出将其作为直观理解诸如氦原子之类的物理系统的工具。
引力三体问题也被通过广义相对论进行了研究。在物理上,相对论性的处理在引力场非常强的系统中变得非常必要,比如在黑洞的视界附近。然而,相对论性问题比牛顿力学困难得多,需要复杂的数值技术。即使是完整的两体问题(即任意质量比)在广义相对论中也没有严格的解析解。
N体问题
三体问题是N体问题的一个特例,它描述了n个物体在其中一种物理力(如重力)下如何运动。这些问题具有收敛幂级数形式的全局解析解,比如,Karl F.Sundman证明n=3的情况,qaudong Wang证明n>3的情况。然而,Sundman级数和Wang级数收敛速度太慢,无法用于实际目的;因此,目前有必要通过数值分析以数值积分的形式来近似解,或者在某些情况下,采用经典三角级数近似。原子系统,例如原子、离子和分子,可以用量子N体问题来处理。在经典物理系统中,N体问题通常是指一个星系或一个星系团;行星系统,如恒星、行星及其卫星,也可以被视为N体系统。一些应用可以方便地用扰动理论来处理,其中系统被认为是一个两体问题加上导致偏离假设的无扰动两体轨道的附加力。
三体小说
三体问题被中国作家刘慈欣用于科幻小说三部曲中的情节设计,也被用于作为第一卷和整个三部曲的书名。
编者推荐
书籍推荐
小说《三体》
《三体》是刘慈欣创作的系列长篇科幻小说,由《三体I 地球往事》、《三体Ⅱ·黑暗森林》、《三体Ⅲ·死神永生》组成,第一部于2006年5月起在《科幻世界》杂志上连载,第二部于2008年5月首次出版,第三部则于2010年11月出版。作品讲述了地球人类文明和三体文明的信息交流、生死搏杀及两个文明在宇宙中的兴衰历程。其第一部经过刘宇昆翻译后获得了第73届雨果奖最佳长篇小说奖。

《三体》小说,作者:刘慈欣
集智文章
混沌与非线性:三体问题和蝴蝶效应之谜
所谓的混沌现象,其实是一种由确定的规则所产生的看起来随机的现象。混沌系统之所以看起来混乱,是因为它对初始误差非常敏感,导致我们无法准确预测混沌系统的长期行为。而初值敏感性的产生机理,就在于非线性相互作用的存在。在复杂系统中,混沌与秩序同时并存。
《自然》杂志对话刘慈欣:《三体》写作、灵感以及中国科幻
《三体》三部曲的作者刘慈欣是一位备受赞誉的中国作家。在中国,他曾多次获得银河奖(中国幻想小说界的最高荣誉奖项)。当三部曲的第一部《三体》,由刘宇昆翻译成英文并由Tor出版后,好评如潮,一举获得了2015年雨果奖最佳长篇小说奖。《自然》杂志“未来”专栏(Futures)的Preston Grassmann对话刘慈欣,讨论了关于写作、灵感以及中国科幻等问题。
百科项目志愿者招募


如果你有意参与更加系统精细的分工,扫描二维码填写报名表,我们期待你的加入!

来源:集智百科
编辑:王建萍
-
自由度:系统状态相空间的维数 | 集智百科 -
量子信息与量子计算预读班:追踪量子信息革命交叉前沿 -
网络中心性:多种中心性指标的定义与对比 | 集智百科 -
网络枢纽的涌现及其属性 | 集智百科 -
级联失效:从电网、计算机网络到金融 | 集智百科 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会
点击“阅读原文”,阅读词条三体问题原文与参考文献
本篇文章来源于微信公众号: 集智俱乐部










