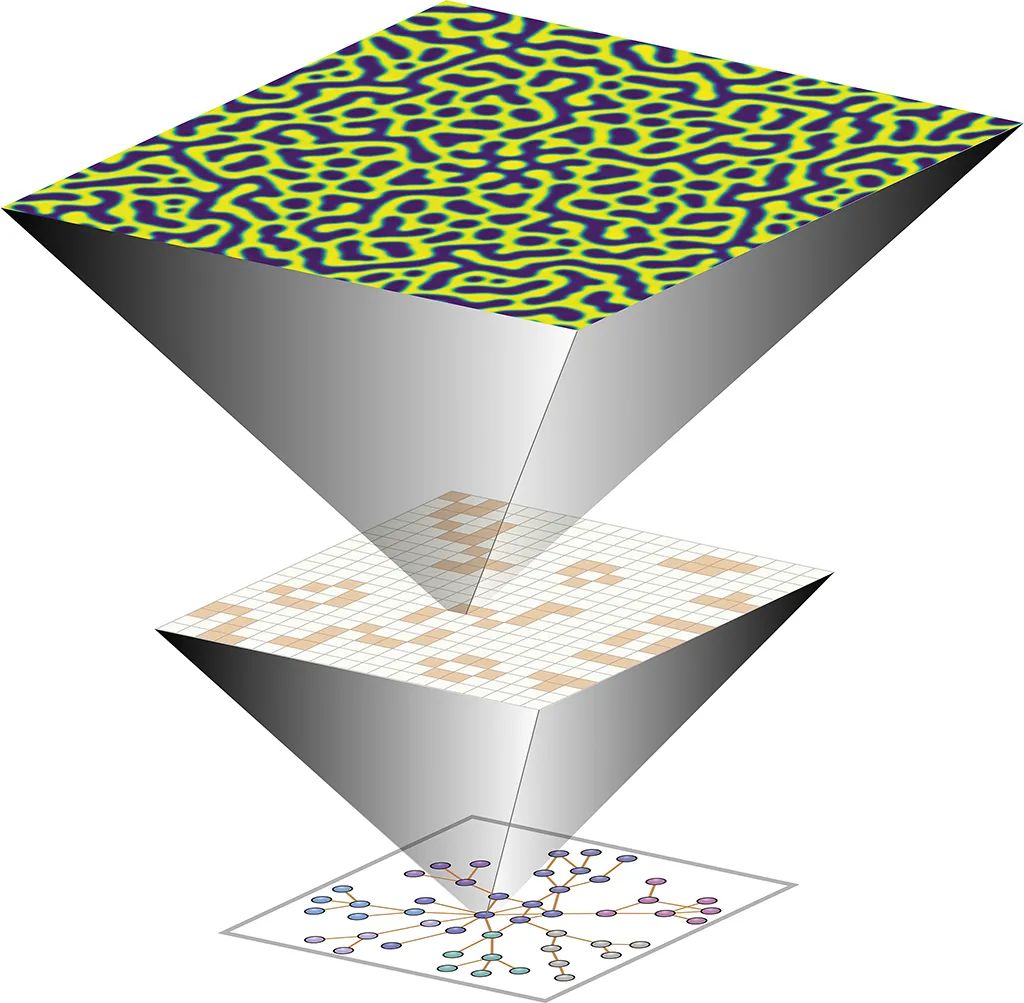
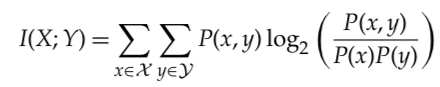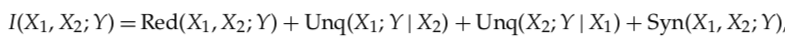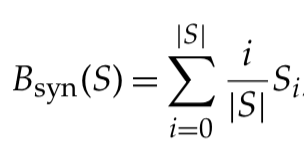之前的研究表明,还原并非总是好的科学策略,一些情况下,降维可以增加系统元素之间的依赖性,使得粗粒化的宏观尺度比底层微观尺度携带更多有效信息,这种现象被称为“因果涌现”。因果涌现理论的提出者 Erik Hoel 和同事在2022年5月发表的最新论文「作为信息转换的涌现:一个统一理论」中,提出了一个基于信息转换的关于涌现的数学框架,证明粗粒化可以将信息从一种“类型”转换为另一种。从这个视角而言,从微观到宏观的因果涌现可以理解为,因果无关信息到因果相关信息的转换。本论文收录于 The Philosophical Transactions of the Royal Society A 2022年5月的主题特刊“复杂物理和社会技术系统中的涌现现象:从细胞到社会”。
研究领域:因果涌现,因果关系,因果量化

论文题目:
Emergence as the conversion of information: a unifying theory
https://royalsocietypublishing.org/doi/full/10.1098/rsta.2021.0150
还原论是科学中的经典原理。与此同时,科学本身形成了多样的树状结构,包含不同时空尺度的元素,如量子物理中的波、化学中的分子、生物学中的细胞,一直到宏观经济学和社会学。另一方面,宏观尺度的描述,如细胞的生物物理模型、计算机中的机器代码或食物网中的生物体,通常被认为是反映了功能的某种内在尺度,不能通过还原来改进。这导致了科学的理论与实践之间存在矛盾。
解决这一矛盾的一个办法是还原论的“零假设”:所有宏观描述是某种形式的降维(如粗粒化),仅在计算约束下有用。根据这个假设,这是因为底层的微观尺度包含所有信息,信息压缩只是为了在宏观层面上分析和理解系统。对于给定信息源,信息压缩可能是无损的或有损的,但永远不可能导致总体的信息增加。既然在宏观尺度上总体信息不可能增加,那是否意味着宏观尺度不能在微观尺度之外提供更多东西呢?
因果涌现理论从信息论视角对系统的不同尺度进行了明确比较,该理论认为,宏观尺度的因果关系可能比微观尺度更强(比如做更多功、更有预测性、信息量更大)。总的来说,因果涌现理论的观点是,由于宏观状态更具有确定性、更不简并,它们做了最多功来选择输出,有效信息可以识别功在哪个时空尺度最大化,使得功最大化的尺度就是最具因果关系的尺度,无论是宏观还是微观。(参看《量化因果涌现表明:宏观可以战胜微观》)
信息不可能凭空产生。系统整体的信息,无论是用系统状态的熵、描述总体相关性的互信息来度量,在宏观尺度上永远不可能增加。然而,信息可以从一种类型转换为另一种类型,除了尺度不同外没有其他变化,这意味着在宏观尺度特定类型的信息可能增加。从这个角度而言,可以认为因果涌现是一种更高尺度的信息转换(information conversion),在宏观尺度,因果相关的信息增加。
本文试图用互信息证明跨尺度的信息转换。以布尔网络为例,其过去和未来状态之间的互信息在宏观尺度上只会减少或保持不变,通过将信息分解为部分信息原子(PI atoms),可以看到整体信息在系统的所有元素上如何分布。研究表明,经过粗粒化,微观尺度的冗余信息可以转换为宏观尺度的协同信息,即使在没有互信息丢失的情况下,这种效应也存在。
布尔网络(Boolean network)是复杂系统科学中的一个典型模型。在布尔网络中,随着时间推移,每个节点的状态可以根据其所有父节点状态的逻辑函数而变化。系统可以看作是信息从过去通过现在的通道传递到未来。我们可以通过计算网络的过去和未来状态之间的互信息来量化这种信息流。具体而言,如果X表示网络的过去状态,Y表示未来状态,它们的互信息 I(X,Y) 量化了关于系统过去状态的知识在多大程度上减少了对未来状态的不确定性。
计算互信息可以获得系统动力学中的总信息量,但如果系统中包含两个以上变量,互信息无法直接洞察,信息在多个相互作用变量的集合上如何分布。例如,考虑两个源变量X1和X2调节单个目标变量Y的情况:我们很容易确定X1和Y之间共享的信息,即互信息 I(X1;Y)(X2与之类似);也可以计算出联合互信息 I(X1, X2; Y);但无法确定哪些信息与哪些变量组合相互关联。比如,一些关于Y的信息可能是X1单独提供而不包含在X2中的;一些可能是X1和X2之间冗余共享的;一些信息则可能只有X1和X2的联合状态才能共同揭示,而不能从其中任何一个变量单独获得。
部分信息分解(Partial Information Decomposition, PID)提供了一个方法,可以将互信息进行原子化拆分。对于上面的例子,两个源变量(X1和X2)的联合状态和单个目标变量(Y)之间的互信息 I(X1, X2; Y) 可以分解为如下的“部分信息原子”之和:
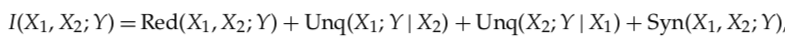
其中 Red(X1, X2; Y) 对应前面提到的X1和X2之间冗余共享的关于Y的信息,我们称之为冗余信息;Uniq(X1; Y|X2) 表示X1单独提供而不包含在X2中的关于Y的信息,称为X1的单独信息;Syn(X1, X2; Y) 表示只有X1和X2的联合状态才能共同揭示的关于Y的信息,称为协同信息。
一个形象的例子是,我们的两只眼睛会共同接收视野中的信息传输给大脑,如果闭上一只眼睛,我们会发现,每一只眼睛都提供了视野边缘的一些“单独信息”;与此同时,一些信息是两只眼睛都能捕捉到的“冗余信息”,比如与颜色有关的信息往往是冗余的,因为它对于识别物体非常重要,眼睛通过这种冗余机制确保了视觉的稳健性与可靠性。另外,关于空间深度的立体信息是需要两只眼睛相互协作才能提供的“协同信息”,它帮助我们的大脑感知到第三维度。简而言之,互信息分解公式可以粗略表示为:
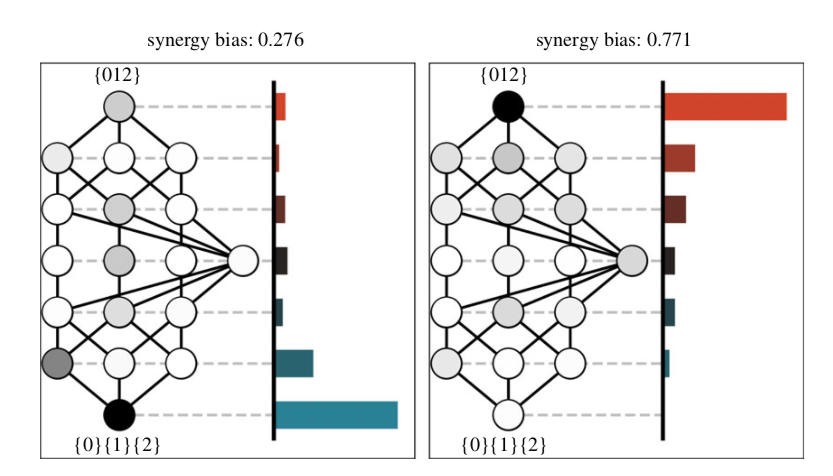
随着源变量的数量增加,需要考虑的源变量组合的数量以超指数增长,部分信息分解也变得非常复杂。不过有趣的是,这些源变量的组合会自然地组织成一个部分有序的格点,越是冗余的信息原子越靠近格点底部,协同信息则靠近格点顶部,我们称之为部分信息格点(PI lattice)。例如对于三个源变量的情况(图1),PI 格点的底部是 {0}{1}{2},表示三个源变量中冗余存在的关于目标变量的信息;顶部是{012},表示只有联合考虑三个源变量时才能揭示的关于目标变量的信息,不能通过任何“更简单”的源变量组合来获得。
图1. 在两幅图中,左侧表示三个源变量的部分信息格点,右侧表示部分信息谱。根据系统的PI格点可以构建PI谱,计算信息原子在格点中的相对位置,以此衡量信息的协同程度。左边的系统协同偏差较低,关于未来状态的大部分互信息冗余地包含在所有元素({0}{1}{2})或其他高度冗余的PI原子(如{0}{1})中。右边的系统中,三个元素具有高度的协同偏差,关于未来状态的信息大部分只存在于三个元素的联合状态({012})中。
对于包含超过两个元素的系统,我们不再能将互信息简单地拆分为冗余信息、协同信息、单独信息,而是需要构建一个部分信息谱(Partial Information Spectrum),计算信息原子在 PI 格点中的相对位置是靠近底部还是顶部,以此衡量信息的冗余和协同程度。
PI 格点中越是靠近顶部的原子包含更多协同信息,同一层的信息原子具有相同的冗余-协同比率,因此可以将部分信息谱 S 看作一个有序序列。我们进一步定义协同偏差(synergy bias),定量比较不同 PI 格点顶部所包含的协同信息比例。系统的协同偏差定义为,每一层的归一化部分信息(Si 是第 i 层的所有信息原子占总互信息的比例)乘以该层相对于格点底部的距离(层数 i 除以格点总层数 |S|):
协同偏差越大,表明大部分部分信息存在于元素的协同关系中;协同偏差越小,表明大部分部分信息冗余存在于多个元素中。
论文首先以逻辑门为例,展示跨尺度信息转换。通过将3个基本逻辑门(与、或、异或)分解为具有更简单机制的微观尺度逻辑门,可以直接比较微观尺度和宏观尺度各自的部分信息分布。
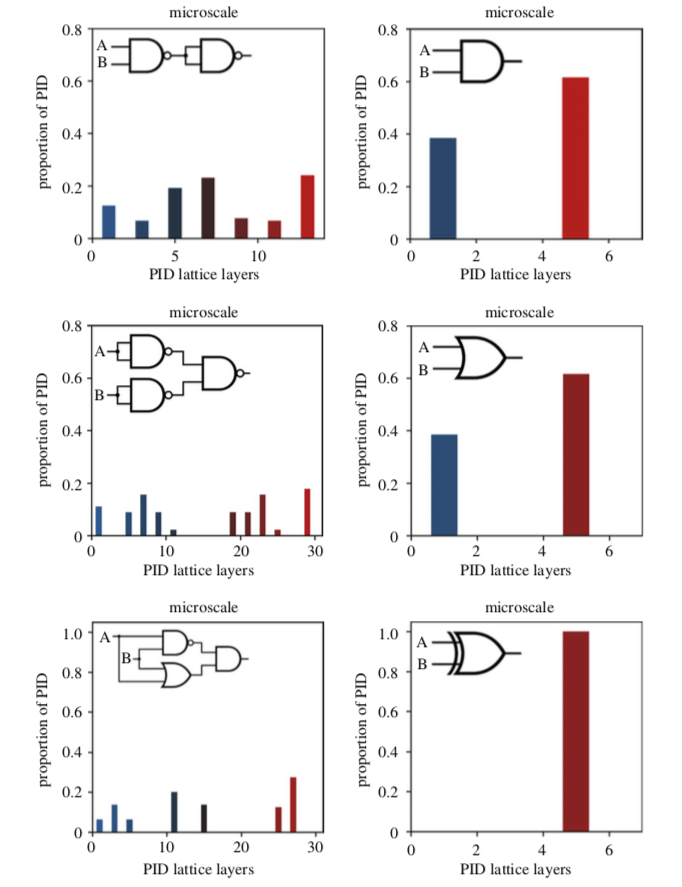
以「异或门」(XOR)为例,如图2所示,它在宏观尺度包含3个元素(XOR,输入A和B),在微观尺度可以分解为一个「非门」、一个「与门」和一个「或门」组成的网络,共包含5个元素(NAND、AND、OR,输入A和B)。计算相同输入下宏观尺度和微观尺度的互信息可以发现,在微观尺度,系统的互信息为2.5比特,在宏观尺度则是1比特。使用PID对结果进行分解,系统的协同偏差从微观尺度的0.52增加到宏观尺度的0.83(表1)。也就是说,虽然宏观尺度的整体互信息减少,但信息的协同作用增加。对于「或门」和「与门」也是如此,尽管程度较轻。
图2. 三种逻辑门(右侧)及其底层微观尺度逻辑门网络(左侧)的部分信息谱。从上到下分别为:与(AND)、或(OR)、异或(XOR )。协同偏差和互信息如表1所示。
表1. 三种逻辑门的互信息和协同偏差。从微观到宏观,随着粗粒化程度提高,互信息降低,协同偏差增加。
这表明,从微观到宏观尺度,虽然降维减少了系统的总信息量,但“剩余”信息可以在宏观PI格点上移动到更高层级。也就是说,像粗粒化这样的降维可以改变系统PI格点的信息分布,即使这两种尺度只是对同一系统的不同描述。
对于上面的例子,有人可能质疑,从微观到宏观尺度协同信息的比例增加,或许只是因为PI格点底层的冗余信息在降维过程中丢掉了。论文提供了另一个更直接的例子来说明,信息确实是从一种类型转换为另一种类型,即从冗余信息转换为协同信息。
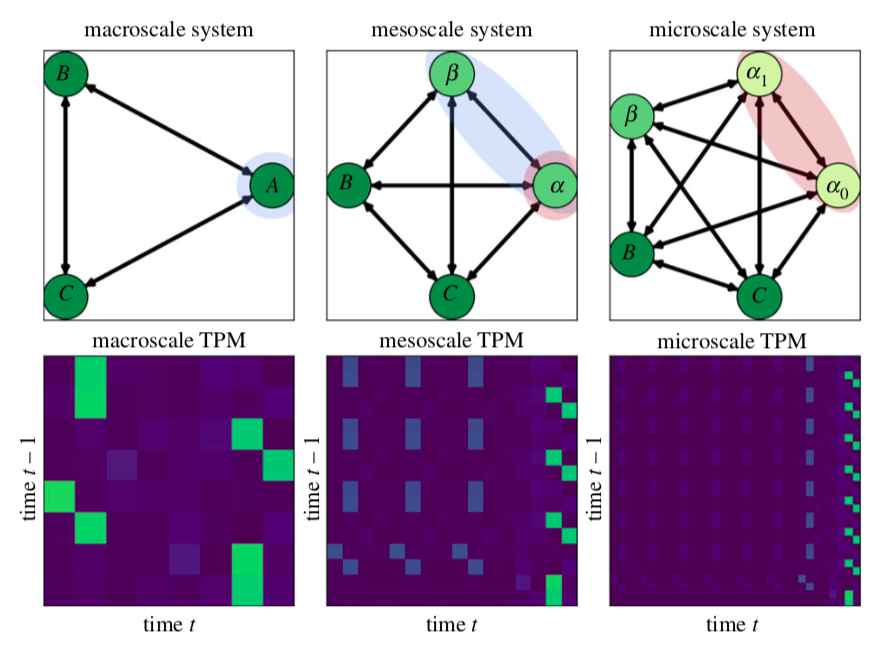
首先生成一个布尔网络(用转移概率矩阵TPM表示)作为起始的宏观尺度,然后如图3所示,将这个网络上的其中一个节点分裂成两个节点,然后继续分裂,就从宏观系统逐步变成更小尺度的中观系统、微观系统。通过在新的扩展状态空间中重新分配转移概率,可以确保随着维度增加,系统的整体互信息保持不变。由于系统互信息在不同尺度保持不变,协同偏差的任何变化必然来自信息转换,而非信息丢失。
图3. 在互信息固定的情况下,从给定的宏观尺度构建微观尺度。左侧为一个三元素系统,选择单个节点 (A) 扩展为两个节点 α 和 β,形成一个四元素系统(中);选择另一个节点 (α) 再次扩展,得到最终的微观系统(右)。在节点扩展过程中,从过去到未来状态的整体互信息保持不变。下面一行是对应的转移概率矩阵(Transition Probability Matrix, TPM)。
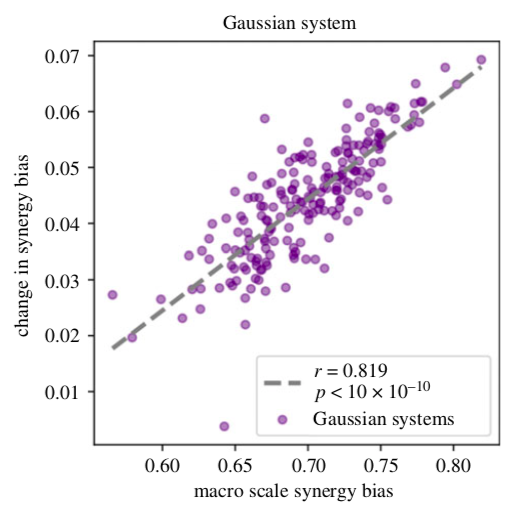
反过来对微观尺度不断进行粗粒化,可以发现,从微观到宏观转换过程中协同偏差的增加,与宏观协同偏差之间具有明显的正相关关系(图4)。这表明即使系统的总互信息在跨尺度情况下保持不变,宏观尺度上协同偏差增加,微观尺度上冗余信息增加。因为总互信息保持不变,宏观尺度上协同信息的增加只可能来自微观尺度上冗余信息的减少。这也证明,降维可以通过将信息更多地转换为协同信息,来增加系统的整体协同性。
图4. 协同偏差的跨尺度变化。从微观尺度到宏观尺度协同偏差的变化与宏观协同偏差两者之间存在明显的正相关关系。
我们看到从微观尺度到宏观尺度信息转换的证据,那它和关于涌现的其他信息论方法有何关系?如何在捕捉因果效应的有效信息(Effective information, EI)测量中发挥作用?
研究已经证明,有效信息的跨尺度变化源自确定性(determinism)和简并性(degeneracy)的变化:
其中确定性衡量从某个状态出发,可以在多大程度上确定性地决定系统的未来状态;一个完全确定性的系统,其当前状态以概率1决定系统下一时刻的状态。简并性衡量当系统处于某个状态时,可以在多大程度上确定系统的过去状态;一个极端简并的系统,其所有过去状态最终都收敛到相同的最终状态,反之,一个完全不简并的系统,其过去状态会确定一个唯一的最终状态。
在一个具有完美因果机制的系统中,每个原因都有一个唯一的结果,每个结果都有一个唯一的原因,它是完全可追溯、完全可预测的。这样的系统,其确定性最大化而简并性最小化,有效信息在宏观尺度不可能增加,因为此时没有可以转换的信息。从这个角度,因果涌现可以理解为,因果无关信息(如状态转变的不确定性)到因果相关信息(有效信息)的转换。
未来的进一步工作可以研究,协同信息在什么尺度达到峰值,或者找到在什么尺度可以最大限度转换信息,同时最小化丢失信息。尽管这项研究证明了一些冗余信息转换为协同信息,究竟是哪些信息改变了形式还有待理解。
这篇论文的假设是,物理之上的其他科学学科以及一般的宏观模型,涉及到冗余信息到协同信息和单独信息的转换,使得这种宏观尺度对实验者非常有用。将这一点与之前的研究联系起来,宏观模型可以通过使模型中变量之间的因果关系更加依赖(通过增加确定性或减少简并性),将因果无关的信息转换为因果相关的信息,实现因果涌现。
需要注意的是,确定变量之间的依赖性在什么尺度更强要容易得多。例如,有研究表明,生物网络比技术或社会网络显示出更多的因果关系。这可能是因为宏观尺度有多种优势,比如随机游走的熵更低,宏观尺度有更高的全局效率。一些初步研究观察了超过1000种蛋白质相互作用组,表明在宏观尺度上更有可能在演化时间内表现出因果涌现。这或许也是控制生物系统如此困难的一个原因:它们将内在的功能尺度隐藏在难以发现的宏观尺度中,这使得生物网络更加稳健,不容易受外部变化影响。
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。同时,新兴的因果表示学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
由北京师范大学教授、集智俱乐部创始人张江和加州大学圣地亚哥分校助理教授尤亦庄等人发起的「因果涌现」系列读书会第二季,将组织对本话题感兴趣的朋友,深入研读相关文献,激发科研灵感。本读书会自2022年5月22日开始,每周日晚19:00举办,预计持续7-8周。欢迎感兴趣的朋友报名参与。

本季读书会详情与报名方式请参考:
因果、涌现与机器学习:因果涌现读书会第二季启动