近日发表于 Nature Computational Science 的一项研究提出了一个小且易于分析的神经网络,即自适应伊辛类模型(adaptive Ising class)。通过从静息状态的大脑活动记录中推断模型的参数,研究表明:在静息大脑中,特定标度的振荡和无标度雪崩可以在接近非平衡临界点时(自持振荡开始时)共存。
关键词:大脑临界点,伊辛模型,雪崩,振荡,同步,集体行为
Nature Computational Science | 来源
郭瑞东 | 译者
朱欣怡 | 审校
生物神经网络表现出大量由神经网络同步引起的大规模集体行为。振荡[1]是一种具有明确尺度的典型神经活动同步模式。相比之下,神经元雪崩[2]是无标度的(即缺乏典型的时间或空间特征)神经活动级联,通常标志着大脑进入临界态。振荡与雪崩这样两种对比鲜明的行为同时涌现,表明这是一种尚未被完全理解的有趣二分法。
尽管已有分别解释振荡和雪崩的模型,但它们通常不能同时解释这两种现象,并且存在一定的局限性。一方面,受统计物理启发的简单模型无法量化大脑神经活动(特别是超越神经元尺度的雪崩)的复杂性。另一方面,设计用于捕获特定脑振荡的半现实但复杂的模型,无法解决大脑临界性,无法再现神经元雪崩。在这两种情况下,目前的模型都过于复杂以至于无法分析,或难以从数据中严格推断。
我们假设,用来调整神经网络兴奋性的基本反馈机制,可以解释相互对立的特定尺度振荡和无标度雪崩为何可以共存。为了验证模型提出的假设,我们的模型建立在神经网络和自旋系统[3]之间的类比之上,并提出了一个伊辛模型的非平衡扩展(为使该模型具有自适应性,模型内有一个额外的反馈回路)(图1a)。由于这种自适应反馈,神经元的动力学被实时网络活动驱动,导致众多集体行为的涌现。
如同以前的静态伊辛模型在神经系统中的应用[4],自旋是对单个神经元的尖峰的建模,对应单个神经元的二元性质(激活与静息)。因此,这类模型中最简单的结构就是一个受全局自适应反馈的全连接网络,既能够做解析分析,同时又能研究微观动力学(单个神经元)。然后我们能构建该模型的相图。
得到解析解之后,通过对模型的两个参数进行易处理的推断,我们就能比较该模型与磁电图(magnetoencephalography,MEG)的记录。尽管推断出的模型很简单,但它量化地再现了在宽尺度上的大脑动力学,从单一MEG传感器上记录的振荡(图1b)到遍布多个传感器、跨越多个时间窗口的复杂时空组织的神经元雪崩(图1c)。该推断令人信服地表明,在自持振荡的开始阶段,接近但略低于模型的非平衡临界点时,振荡和雪崩同时出现。
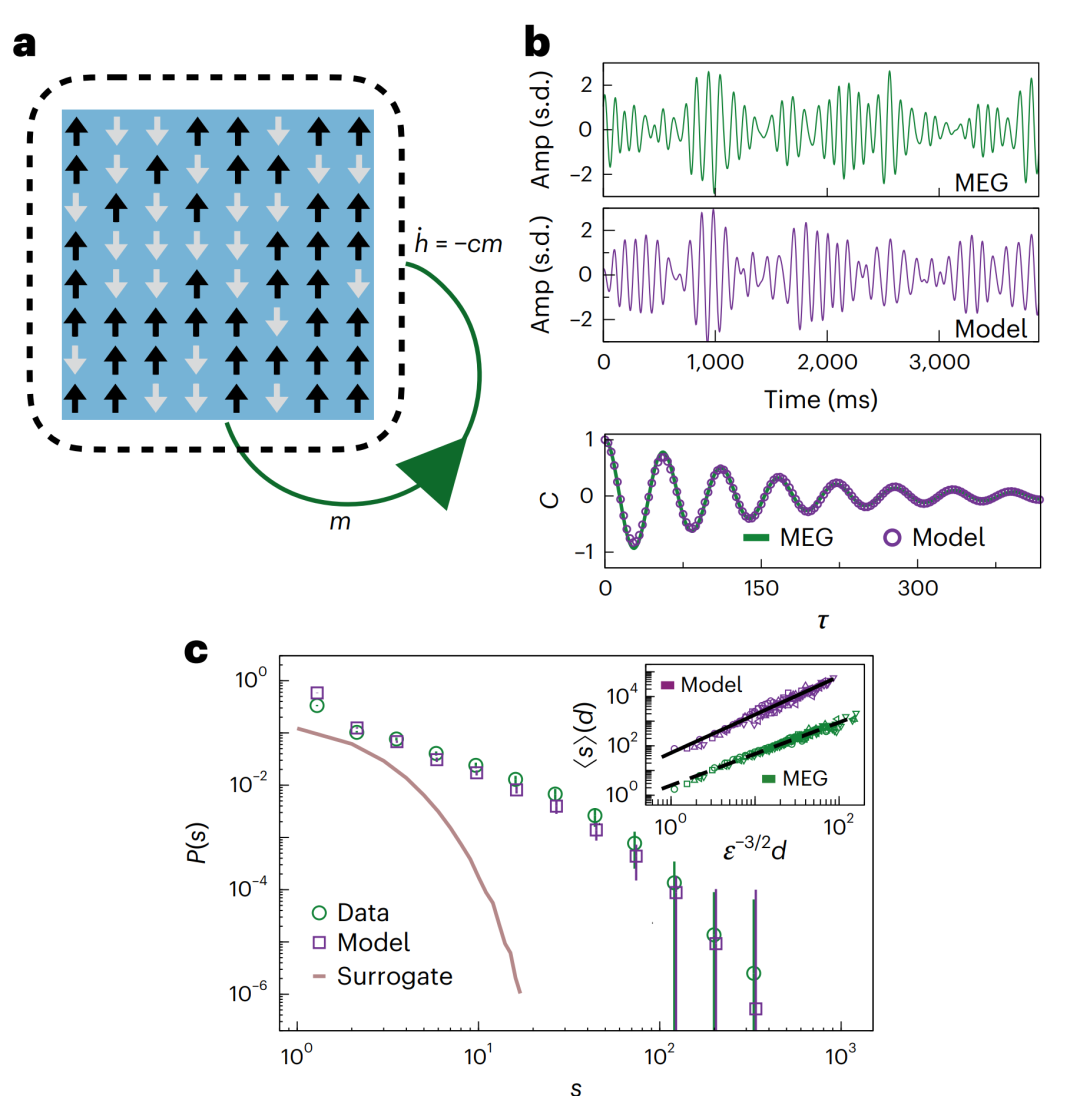
图1:静息脑中振荡和雪崩共存与亚临界自适应伊辛模型。
a, 模型的示意图。相互作用的自旋取值为±1(分别为向上和向下箭头)。外部场 h(t) 随时间变化,模拟依赖于活动的反馈机制。其中m代表网络活动。
b,上图:α带通滤波的脑磁(MEG)信号(绿色)和含参模型的模拟活动(紫色);(Amp代表振幅;s.d.代表标准偏差)下图:通过将自相关函数C(紫色点)的解析形式拟合到从脑磁(MEG)信号数据(绿色线)估计的自相关来推断模型参数。τ 代表时滞。
c,雪崩大小 s 的分布情况,P(s):脑磁数据和模型(误差条为受试者或模型模拟的平均值,分别为 ±s.d.);Surrogate:来自于有扰乱相位的数据的大小分布;插入小图:平均雪崩大小的分布;<s>,以其持续时间(d)的幂律缩放;𝜺:测量雪崩的时间箱。
通过将模拟系统分割成多个自旋的组,我们可以模拟皮层上由多个MEG传感器捕获的信号。在这种情况下,由成组自旋产生的磁化,可以被认为是MEG传感器捕获的磁场的代理。
我们在实际观察以及模型模拟中都发现的非指数与尺度不变的网络激活分布这两者之间存在定量的对应关系。这种极端事件的空间-时间组织强烈表明了网络状态接近于临界状态。总的来说,我们的模型提供了一个广泛的对跨空间和时间尺度的大脑动力学描述。
在未来,我们计划探索连通性的作用,而不仅仅是我们所介绍的简单的全对全平均场模型(all to all mean-field),并扩展该模型,以包括真实神经网络的拓扑特征和不同的细胞类型(例如,抑制性与兴奋性神经元)。这种方法将可能导致在新的动力学类型,如皮层波上的更好数据拟合。
此外,关键是要用不同类型的大脑数据,如同步尖峰和局部场电位势记录来测试该模型。在这种情况下,一个真正成功的模型将可同时考虑到在微观层面上的统计数据(即单个神经元的棘波)和中观尺度大局部场电位。重要的是,我们所使用的方法是将经验数,通过参数推断映射到自适应伊辛模型相位中的一个确定区域,可用以进一步量化和澄清大脑临界值与健康、发育或病态大脑动力学之间的关系。
我们一直在从不同的角度研究复杂的生物网络中的集体动力学,以及更一般的复杂的生物网络。我们中的一些人对大脑节律与神经系统雪崩之间的关系进行了实证研究。其他人对连接自旋模型和雪崩与振荡之间的共存机制感兴趣。目前的研究代表了上述两种研究方法的趋同。
Cristiano Capone, INFN, Sezione di Roma
作者提出了一种新的神经网络类型,可以同时解释大脑活动中特定尺度下的振荡和无标度的雪崩。重要的是,这种模型可以进行解析分析,其参数可以从人类大脑活动记录中严格推断出来。此研究结果表明,大脑活动中的振荡和雪崩的共存出现在非平衡临界点附近。
Nature Computational Science 助理编辑 Ananya Rastogi
这项工作让我印象深刻,因为作者提出了一个反馈驱动的伊辛类神经元网络模型,能够重现大脑活动中的无标度雪崩和尺度特定的振荡,这种行为是现有理论模型没能捕捉到的行为。
本文翻译自 Nature Computational Science 评论文章
原文题目:Oscillations and avalanches coexist in brain networks close to criticality
https://www.nature.com/articles/s43588-023-00411-8
1. Buzsaki, G. & Draguhn, A. Neuronal oscillations in cortical networks. Science
304, 1926–1929 (2004). A review article on brain rhythms.
2. Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177 (2003). This paper reported neuronal avalanches.
3. Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA 79, 2554–2558 (1982). A seminal work on the application of spin models to the study of neural networks.
4. Tkacik, G., Prentice, J. S., Balasubramanian, V. & Schneidman, E. Optimal population coding by noisy spiking neurons. Proc. Natl Acad. Sci. USA 107, 14419–14424 (2010). This work investigated optimal population coding in neural networks.
为了促进神经科学、系统科学以及计算机科学等多领域学术工作者的交流合作,吸引更多朋友共同探索脑科学与类脑研究,周昌松、臧蕴亮、杨冬平、郭大庆、陈育涵、曹淼、刘泉影、王大辉、刘健、王鑫迪等来自国内外多所知名高校的专家学者在集智俱乐部共同发起「神经动力学模型」读书会,历时四个月研讨,近日圆满结束。
本季读书会形成了聚集500+成员的神经动力学社区,积累了40+小时综述、解读、研讨的视频记录,以及多篇社区成员总结的词条、笔记、翻译、科普资料等。现在报名加入读书会,即可加入社区交流讨论(微信),并解锁相关视频、文本资料。我们对脑的探索才刚刚起航,欢迎你一道参与,共同点亮更多脑科学研究的岛屿!
详情请见:
500+神经动力学社区成员,邀你共同点亮更多脑科学研究的岛屿