寻找网络中的关键节点和边是网络科学中的一个基本问题。圈结构作为沟通高阶网络和普通网络的桥梁受到越来越多的关注。是否可以提出一个排序算法衡量圈结构的重要性?近日发表于PRL的这篇文章提出,Fiedler值(Laplacian 矩阵的次小特征值)是网络一致性动力学中的重要指标,越是重要的圈结构对网络动态行为贡献越大。
本文介绍我们最近发表在物理学顶级期刊 PHYSICAL REVIEW LETTERS 上的论文 [1] :
Searching for Key Cycles in a Complex Network, Phys. Rev. Lett. 130, 187402 (2023)
https://link.aps.org/doi/10.1103/PhysRevLett.130.187402
论文作者:蒋思杨、周进、Michael Small、 陆君安、张妍琪
在网络中寻找重要的节点(或节点组)和边(或圈)是网络科学中的一个基本问题,圈结构作为沟通高阶网络和普通网络的桥梁也受到了越来越多的关注 [2,3]。我们知道,像天文学家利用恒星光谱可以确定遥远恒星的组成一样,可以从网络图的特征值谱推演出网络的结构和许多定量的物理性质。
在研究网络一致性动力学中节点或者节点组重要性时,我们提出图的Laplacian矩阵的删后矩阵最小特征值作为衡量指标 [4,5]。那么研究网络圈(或边组)的重要性时,我们应该采用怎样的衡量指标呢?
Fiedler值(Laplacian 矩阵的次小特征值)是网络一致性动力学中的重要指标,清晰地认知Fiedler值是非常关键的。
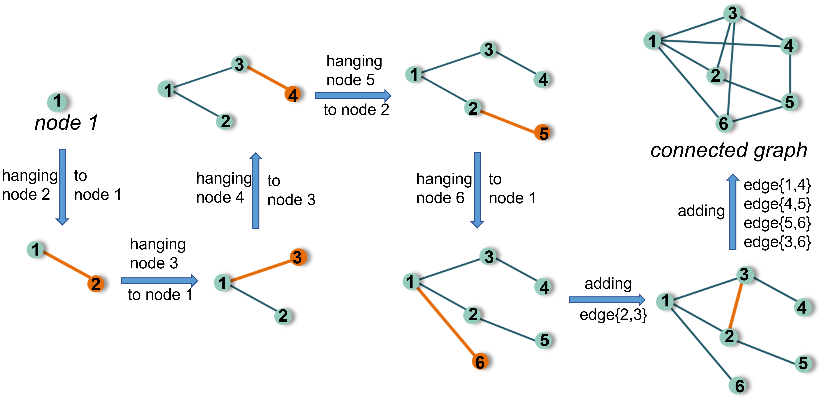
我们首先解释了为什么网络圈结构对于一致性动力学是重要的。任意一个连通网络可以被认为是通过先添加节点-边对(悬挂运算)来构建核心树(无圈),这样的运算会降低网络的Fiedler值;然后添加额外的边(加边运算)生成此网络,这增加了Fiedler值。
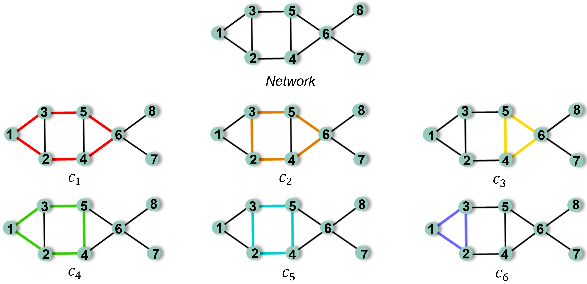
第二步运算与圈的产生有关,因为每增加一条新边至少会产生一个新圈 (见图1)。圈的出现预示着Fiedler值的增加,因而圈结构在一致性动力学的研究中是重要的。例如:当网络规模很大时,环状网络的Fiedler值是链状网络的4倍。
接下来,我们给出网络中圈的重要性排序。圈的重要性受长度及位置影响,如何给出某一指标同时包含这两个信息?这篇文章利用网络动力学和矩阵特征值扰动理论 [6],导出衡量网络中的圈在网络动力学中重要性的新指标,它完全由 Fiedler 向量x2(G) (Fiedler值对应的特征向量)的分量决定。设网络有k个圈Ci(i=1, 2, …k),对圈Ci的所有边施加扰动ε,扰动后Fiedler值的一阶改变量为:
我们认为越敏感的圈越重要,越容易影响网络动力学。进而,我们给出圈重要性的指标值(指标值越大圈越重要):
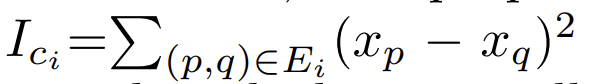 ,
我们可以看到圈的位置优势由Fiedler向量分量决定,圈的长度优势由求和项数目决定。指标值有双重的含义:(1) Fiedler值随圈权重变化的初始斜率(见图2)。(2)由 Laplacian谱理论知λ2=∑p, q∈E’(xp–xq)2,E’为网络中的所有边。可见网络中所有边的贡献总和为Fiedler值;而圈中边的贡献总和为指标值。一个是圈的未来贡献趋势,一个是圈已经产生的贡献,都可由指标值刻画。
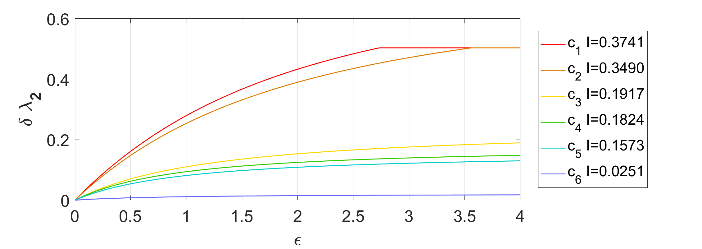
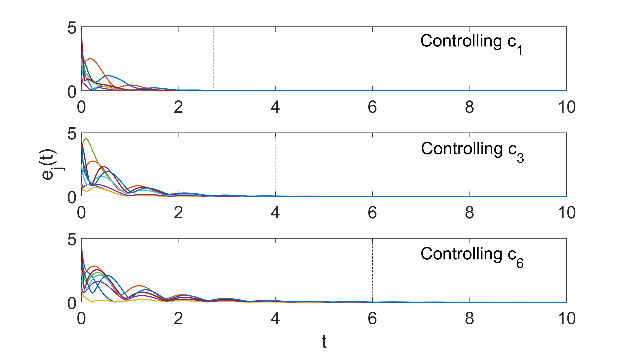
我们在图2中给出一个网络中圈的重要性排序结果,有趣地发现位置好的小圈会比某些大圈更重要,如长度为3的圈C3比长度为5的圈C4更重要;并且排序随圈权重的增加基本上是稳定的(从这6个圈的敏感性排序可以看出,虽然理论上要求ε<<1,实际上ε从0到4, ICi排序基本上是稳定的)。此外,排序结果能应用于边自适应牵制控制同步 [7](自适应增加边组的权重来促进同步),如图3可见控制效率与排序结果一致。
图2 一个含有6个圈的网络以及Fiedler值随圈权重的变化图
最后,我们在图4中研究了秀丽线虫新陈代谢网络的重要三角形分布,发现节点56是关键节点,它与其他分量的差值较大。关键节点和关键圈之间可能存在着深刻的关系。此外,不重要的三角形往往是低度节点连接的三角形,但重要的不一定由高度节点连接产生。这些发现为实际应用提供了一些潜在信息。
,
我们可以看到圈的位置优势由Fiedler向量分量决定,圈的长度优势由求和项数目决定。指标值有双重的含义:(1) Fiedler值随圈权重变化的初始斜率(见图2)。(2)由 Laplacian谱理论知λ2=∑p, q∈E’(xp–xq)2,E’为网络中的所有边。可见网络中所有边的贡献总和为Fiedler值;而圈中边的贡献总和为指标值。一个是圈的未来贡献趋势,一个是圈已经产生的贡献,都可由指标值刻画。
我们在图2中给出一个网络中圈的重要性排序结果,有趣地发现位置好的小圈会比某些大圈更重要,如长度为3的圈C3比长度为5的圈C4更重要;并且排序随圈权重的增加基本上是稳定的(从这6个圈的敏感性排序可以看出,虽然理论上要求ε<<1,实际上ε从0到4, ICi排序基本上是稳定的)。此外,排序结果能应用于边自适应牵制控制同步 [7](自适应增加边组的权重来促进同步),如图3可见控制效率与排序结果一致。
图2 一个含有6个圈的网络以及Fiedler值随圈权重的变化图
最后,我们在图4中研究了秀丽线虫新陈代谢网络的重要三角形分布,发现节点56是关键节点,它与其他分量的差值较大。关键节点和关键圈之间可能存在着深刻的关系。此外,不重要的三角形往往是低度节点连接的三角形,但重要的不一定由高度节点连接产生。这些发现为实际应用提供了一些潜在信息。
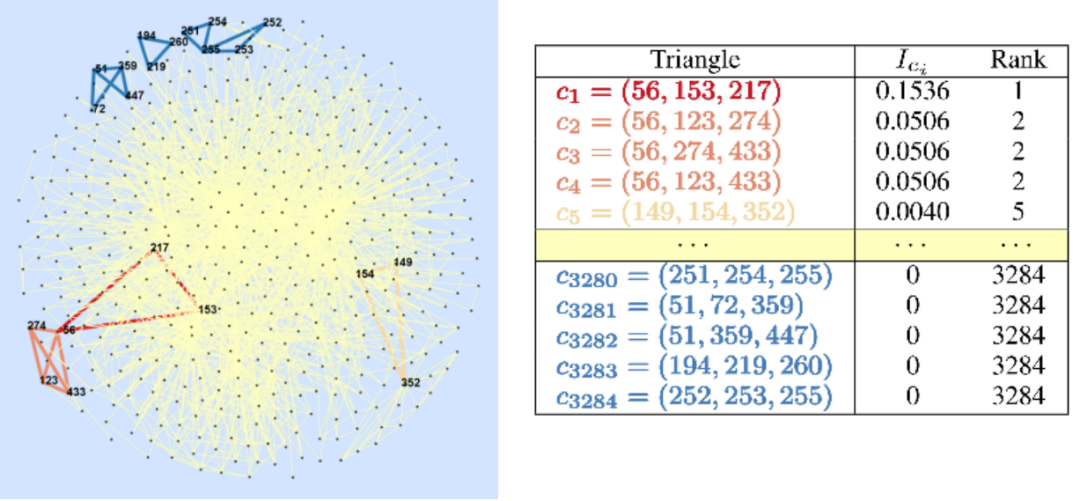
图4 线虫新陈代谢网络的三角形分布情况(前5后5)
总之,文章首次定量刻画了圈的动力学与图的 Fiedler 向量的本质关系,排序结果对扩散分析、牵制控制同步起指导作用。因此,ICi在研究网络动力学中具有重要的意义。同时,我们的工作可以拓展至网络的任意结构(边、四面体等等),可望在最优网络设计、网络的鲁棒性、脆弱性以及网络攻击和防御等方面得到广泛的应用。
[1] S.Y. Jiang, J. Zhou, Michael Small, J. A. Lu, and Y. Q. Zhang, Searching for Key Cycles in a Complex Network, Phys. Rev. Lett. 130, 187402 (2023).
[2] G. Bianconi and A. Capocci, Number of loops of size h in growing scale-free networks. Phys. Rev. Lett. 90, 078701 (2003).
[3] T. L. Fan, L. Y. Lü, D. H. Shi, and T. Zhou, Characterizing cycle structure in complex networks, Commun. Phys. 4, 272 (2021).
[4] J. Zhou, X. H. Yu, and J. A. Lu,Node Importance in Controlled Complex Networks, IEEE Trans. Circuits Syst. II Express Briefs. 66 (3): 437-441 (2019).
[5] H. Liu, X. H. Xu, J. A. Lu, G. R. Chen, and Z. G. Zeng, Optimizing Pinning Control of Complex Dynamical Networks Based on Spectral Properties of Grounded Laplacian Matrices, IEEE Trans. Syst. Man Cybern. 51(2): 786-796 (2021).
[6] J. H. Wilkinson, The Algebraic Eigenvalue Problem (Clarendon Press, Oxford, 1965).
[7] W. W. Yu, P. DeLellis, G. R. Chen, M. di Bernardo, and J. Kurths, Distributed Adaptive Control of Synchronization in Complex Networks, IEEE Trans. Autom. Control 57 (8): 2153-2158 (2012).
陆君安:武汉大学数学与统计学院二级教授、博士生导师。在复杂网络同步控制和识别、多层网络、非线性动力学、混沌及应用数学相关领域取得创新性成果,发表学术论文260余篇,引用10000余次,合著4部,H指数47。2014至2019年入选爱思唯尔(Elsevier)中国高被引学者榜(数学类)。曾获2008和2016年度国家自然科学二等奖、2007年度教育部自然科学一等奖、2013年度和2006年度湖北省自然科学一等奖和二等奖、1996年度国务院政府特殊津贴。
周进:武汉大学数学与统计学院教授,博士生导师。主要研究方向为多层网络、高阶网络、同步、控制、非线性系统等等。在SCI、EI发表学术论文50余篇,其中第一或通讯作者论文44篇,包括物理学顶刊Phys. Rev. Lett.,控制学三大顶刊IEEE Trans. Automat. Contr. (长文和短文)、 Automatica 和SIAM J. Control Optim. 论文被国内国际引用总计2562次,单篇论文引用前两位分别是738次和639次。曾获国家自然科学二等奖、湖北省自然科学一等奖、教育部自然科学一等奖、全国优秀博士论文提名及湖北省优秀博士论文,主持国家自然科学基金项目四项。2021年在“集智俱乐部”组织的第二期和第三期复杂网络课程中,分别做了题为“复杂网络的同步”和“多层网络及其动力学”的专题讲座。
蒋思杨:武汉大学数学与统计学院2021级硕博连读研究生。主要研究方向为网络重要性结构识别、复杂网络同步控制、高阶网络等。
随着对现实世界探索的不断深入,人们发现在许多真实的复杂系统中,组成系统的个体之间不仅存在二元交互关系,也广泛存在多个体同时(或以特定顺序)进行交互,即高阶交互现象。为此,研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型,为复杂网络分析和研究提供了新的思路。
由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学(北京)管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束,第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。



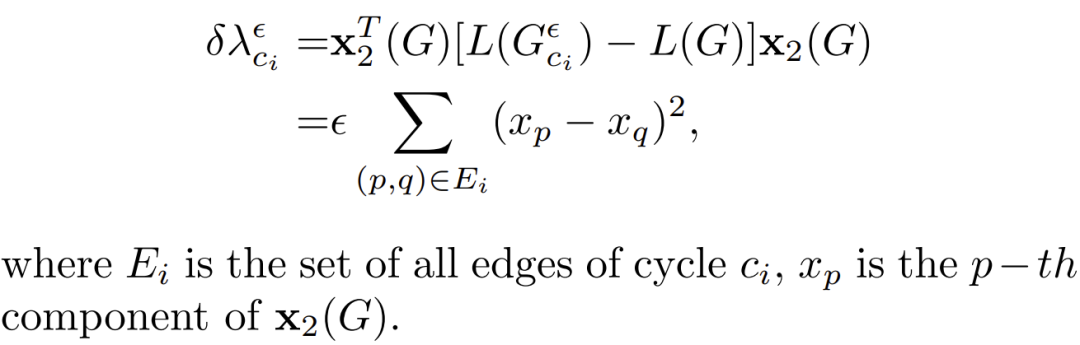
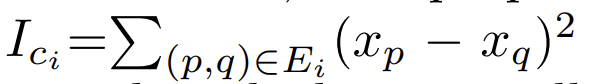 ,
,