数十年来,人工智能的理论发展和技术实践一直与科学探索相伴而生,尤其在以大模型为代表的人工智能技术应用集中爆发的当下,人工智能正在加速物理、化学、生物等基础科学的革新,而这些学科也在反过来启发人工智能技术创新。在此过程中,数学作为兼具理论属性与工具属性的重要基础学科,与人工智能关系甚密,相辅相成。一方面,人工智能在解决数学领域的诸多工程问题、理论问题乃至圣杯难题上屡创记录。另一方面,数学持续为人工智能构筑理论基石并拓展其未来空间。这两个关键领域的交叉融合,正在揭开下个时代的科学之幕。
为了探索数学与人工智能深度融合的可能性,集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师,共同发起“人工智能与数学”读书会,希望从 AI for Math,Math for AI 两个方面深入探讨人工智能与数学的密切联系。本读书会是“AI+Science”主题读书会的第三季。读书会自9月15日开始,每周五晚20:00-22:00,预计持续时间8~10周。欢迎感兴趣的朋友报名参与!
自人工智能诞生以来,探索 AI 在数学研究中的应用一直是一个重要的研究方向,并取得了许多重要成果。在早期符号主义的影响下,吴文俊先生开创了几何定理机器证明。近年来深度学习在数学研究中开始发挥重要作用,并在发现数学规律、生成数学公式、构造数学猜想反例等方面取得了重要进展。另一方面,ChatGPT等大语言模型的诞生提供了一种新的人机交互的方式。如何提升大模型的数学推理能力,并进一步构建人机交互的数学研究平台,辅助数学家更好地开展研究,成为一个非常值得探讨的研究课题。
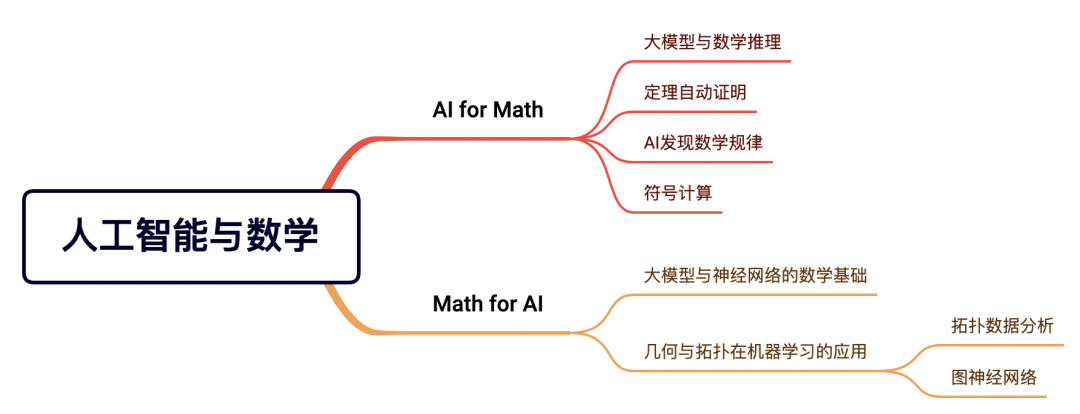
人工智能的理论发展也离不开数学。神经网络以及大模型的可解释性、几何深度学习、拓扑数据分析与动力系统、微分几何、拓扑学等数学分支密切相关。我们将从 AI for Math,Math for AI 两个方面深入探讨人工智能与数学的密切联系,希望对大家有所启发。
从自动定理证明到 AI 发现数学规律,以及几何拓扑、动力系统等数学分支在AI的应用,人工智能与数学一直有着非常密切的联系。在即将召开的读书会中,我们将从 AI for Math,Math for AI 两个方面深入探讨人工智能与数学的密切联系。首先,我们将概述人工智能在数学的应用,并深入探讨大模型与数学推理、定理自动证明、AI发现数学规律、符号计算等方向的研究工作。随后,我们将转向大模型与神经网络的数学基础。最后,我们将深入探讨几何与拓扑在机器学习的应用。我们的目的是通过这样深入的探讨,与大家一起交流学习人工智能与数学的联系,同时揭示未来可能的研究发展方向。
数学结构本身可以看作一个复杂系统,从分析、代数、几何到拓扑,数学对象构成了相互关联的复杂系统。另一方面,复杂科学的研究也离不开数学工具。混沌、非线性等既是重要的数学概念,也是复杂科学的基础概念。人工智能技术的深入发展,将进一步加强数学与复杂科学的深刻联系。数学与复杂科学的方法正逐步渗入到人工智能的研究,并为构建神经网络与大模型的可解释性提供坚实的理论基础。
值得注意的是,与已有的机器学习理论不同,大模型基础理论并不关注具体的优化算法或其泛化表现,而尝试分析模型训练的理想目标是什么。通过分析理想情况得到的理论虽然简单抽象,但却能描绘各种模型各种数据下的共性,进而帮助人们设计出更好的算法,或者对模型表现有更深刻的理解。这和物理学的思维方式非常类似:物理学家会考虑在真空中或者无摩擦的情况下的事物与现象,哪怕这些假设在现实中并不完美成立。对于复杂科学来说,这个思路也应该是一个很好的切入口。
陈小杨,同济大学特聘研究员。2014年5月获得美国圣母大学数学博士学位,2014-2016年在澳门大学从事博士后研究,并于2016年底入职同济大学。陈小杨的主要研究方向为黎曼几何,在 Geometry and Topology, Advances in Mathematics等期刊发表了多篇研究论文。近期,陈小杨与研究团队开展了大模型在基础数学的应用研究,并计划开发机器学习算法用于发现数学规律,构造数学猜想反例等。
袁洋,清华大学交叉信息学院助理教授。2012年毕业于北京大学计算机系,2018年获得美国康奈尔大学计算机博士学位,师从Robert Kleinberg教授。在博士期间,于2014年-2015年前往微软新英格兰研究院做访问学生,并于2016年秋季前往美国普林斯顿大学做访问学生。2018-2019年前往麻省理工学院大数据科学学院(MIFODS)做博士后。袁洋的主要研究方向是智能医疗、AI基础理论、应用范畴论。
夏克林,南洋理工大学副教授。2013年1月获得中国科学院博士学位,于2009年12月至2012年12月在美国密歇根州立大学数学系作为访问学者。从2013年1月至2016年5月,在密歇根州立大学担任访问助理教授。2016年6月,加入南洋理工大学,并于2023年3月晋升为副教授。夏克林的研究专注于分子科学的数学人工智能,在《SIAM Review》、《Science Advances》、《npj Computational Materials》、《ACS nano》等期刊上发表了70多篇论文,并担任了超过10项资助项目的主持人和合作主持人,总金额超过300万新加坡元。
• 数学和AI交叉领域的研究者,包括数学家、计算机科学家和机器学习研究人员等,可以通过分享最新的研究成果和理论探讨,促进知识交流和合作;
• 教育从业者,数学和AI在教育中具有潜在的应用,教师和教育机构工作人员可以参与,了解如何将这些概念融入到教学中,激发学生的兴趣。
• 对计算机和数学感兴趣的本科生和研究生,可以通过这个读书会了解到最新的研究动态和前沿领域,促进学术交流,提高自己的科研能力;
• 对AI和数学交叉领域感兴趣,但没有专业背景的人。这个读书会可以帮助他们建立基础知识,并了解如何将数学与AI结合。
为确保专业性和讨论的聚焦,本读书会谢绝脱离读书会文本和复杂科学问题本身的空泛的哲学和思辨式讨论;不提倡过度引申在社会、人文、管理、政治、经济等应用层面的讨论。我们将对参与人员进行筛选,如果出现讨论内容不符合要求、经提醒无效者,会被移除群聊并对未参与部分退费,解释权归集智俱乐部所有。
本季读书会预计讨论分享8-10次,按暂定框架贯次展开;
每周进行线上会议,由 1-2 名读书会成员以PPT讲解的形式领读相关论文,报名读书会成员可以加入社群,参与讨论,会后可以获得视频回放持续学习,未报名成员可以在集智俱乐部B站或者视频号看公开直播。
从 2023 年 9 月 15 日开始,每周五晚上 20:00-22:00,持续时间预计8-10 周。我们也会对每次分享的内容进行录制,剪辑后发布在集智斑图网站上,供读书会成员回看,因此报名的成员可以根据自己的时间自由安排学习时间。
此次读书会为线上闭门读书会,采用的会议软件是腾讯会议(请提前下载安装)。在扫码完成报名并添加负责人微信后,负责人会将您拉入交流社区(微信群),入群后告知具体的会议号码。
第一步:扫码填写报名信息。

第二步:填写信息后,付费299元。(可参与共创任务获取积分,积分符合标准可以申请退费)
第三步:添加负责人微信,拉入对应主题的读书会社区/微信群。(本读书会可开发票等证明材料,请联系相关负责人沟通详情)
读书会通过共学共研的机制,围绕前沿主题进行内容梳理和沉淀,所以针对于学生,可以通过参与共创任务,获取积分,积分达到退费标准之后,可以直接退费。
在线会议室沉浸式讨论:与主讲人即时讨论交流
交互式播放器高效回看:快速定位主讲人提到的术语、论文、大纲、讨论等重要时间点
高质量的主题微信社群:硕博比例超过80%的成员微信社区,闭门夜谈和交流
超多学习资源随手可得:从不同尺度记录主题下的路径、词条、前沿解读、算法、学者等
参与社区内容共创任务:读书会笔记、百科词条、公众号文章、论文解读分享等不同难度共创任务,在学习中贡献,在付出中收获。
共享追踪主题前沿进展:在群内和公众号分享最新进展,领域论文速递
• 读书会笔记:在交互式播放器上记录术语和参考文献
• 集智百科词条:围绕读书会主题中重要且前沿的知识概念梳理成词条。例如:
• 论文解读分享:认领待读列表中的论文,以主题报告的形式在社区分享
• 论文摘要翻译:翻译社区推荐论文中的摘要和图注
• 公众号文章:以翻译整理或者原创生产形式生产公众号文章,以介绍前沿进展。例如:论文翻译
科普文章翻译
讲座整理
PS:具体参与方式可以加入读书会后查看对应的共创任务列表,领取任务,与运营负责人沟通详情,上述规则的最终解释权归集智俱乐部所有。
以下是由3位发起人老师和多位主讲人推荐的文献列表与相关学习资源。欢迎扫码查看收藏,可以直接跳转链接,下载PDF文件,收藏参考文献列表:
随着人工智能技术的飞速发展,其在数学领域的应用正日益引起人们的关注与热情。AI在数学研究中的应用一直是一个重要的研究方向,并取得了许多重要成果,从大型语言模型到自动证明,再到数学规律的发现,人工智能正逐渐成为数学领域的得力助手。
在数学推理方面,研究人员通过训练大型语言模型,如Llama2,探索了开源模型的基本原理与训练技巧,进一步提升了模型的推理能力。通过思维链的引导,大语言模型在推理能力方面取得了显著进展。此外,将大模型与数学证明相结合,如LeanDojo的实践,为数学定理的自动证明提供了新的思路。
自动定理证明方面的研究也取得了突破,GPT-f等模型在自动证明搜索方面展现出强大的潜力,而进一步的算法改进则使模型能够自动证明各种数学问题,甚至包括国际数学奥林匹克(IMO)的题目。利用自然语言指导定理自动证明,也在一定程度上解决了形式化证明的难题。
AI还在发现数学规律方面发挥了重要作用。通过辅助人类直觉,AI帮助发现了新的数学规律,如扭结不变量、矩阵乘法算法、基本常数等。利用深度学习技术,研究人员甚至能够自动生成数学猜想的反例,推动了数学领域的前沿探索。
同时,符号计算作为数学领域的关键工具,也得到了AI的革新。基于签名的Grobner基算法等方法为符号计算提供了新的思路,使计算更加高效准确。学习选择策略优化算法,以及在Gvw算法框架下改进签名基算法等研究,进一步推动了符号计算领域的发展。
总之,AI在数学领域的应用不仅仅是一种技术革新,更是在拓展人类数学认知边界方面的重要助力。通过大型模型、自动证明、数学规律发现等领域的研究,AI正引领着数学领域的创新与突破,为数学家和研究者提供了前所未有的工具与方法。这一系列研究不仅展示了AI在数学领域的威力,也启示了未来数学与人工智能深度融合的可能性。
Hugo Touvron et al. Llama 2: Open Foundation and Fine-Tuned Chat Models.
arXiv:2307.09288 [cs.CL]
推荐语:详细讲解了开源大语言模型 Llama2 的基本原理与训练技巧。
Jason Wei, et al. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models.
arXiv:2201.11903 [cs.CL]
Kaiyu Yang et al. LeanDojo: Theorem Proving with Retrieval-Augmented Language Models.
https://arxiv.org/pdf/2306.15626.pdf. 2306.15626. [cs.LG].
推荐语: 将大语言模型与lean交互,辅助数学定理证明。
Polu, Stanislas, and Ilya Sutskever. “Generative language modeling for automated theorem proving.”
arXiv preprint arXiv:2009.03393 (2020).
推荐语:提出GPT-f,使用GPT-3级大模型进行自动证明搜索的开山作。
Lample, Guillaume, et al. “Hypertree proof search for neural theorem proving.”
Advances in Neural Information Processing Systems 35 (2022): 26337-26349.
推荐语:用更先进的搜索算法改进了GPT-f,自动证明了十道IMO题目。
Jiang, Albert Q., et al. “Draft, sketch, and prove: Guiding formal theorem provers with informal proofs.”
arXiv preprint arXiv:2210.12283 (2022).
Zhao, Xueliang, Wenda Li, and Lingpeng Kong. “Decomposing the Enigma: Subgoal-based Demonstration Learning for Formal Theorem Proving.” arXiv preprint arXiv:2305.16366 (2023).
推荐语:整合了强化学习和扩散模型的成果,获得了目前自动定理证明的最好结果。
Davies. Alex, et al. “Advancing mathematics by guiding human intuition with AI. ” Nature 600 (2021): 70-74.
推荐语:AI辅助发现扭结不变量,Kazhdan-Lusztig多项式等新规律。
Fawzi. Alhussein, et al. “Discovering faster matrix multiplication algorithms with reinforcement learning”. Nature 610 (2022): 47-53.
Adam. Zsolt. Wagner . “Constructions in combinatorics via neural networks”.
arXiv.org/abs/2104.14516.
Gal Raayoni ,et al. Generating conjectures on fundamental constants with the Ramanujan Machine. Nature , 590 (2021): 67-73.
Brenden K. Petersen, et al. DEEP SYMBOLIC REGRESSION: RECOVERING MATHEMATICAL EXPRESSIONS FROM DATA VIA RISK-SEEKING POLICY GRADIENTS. ICLR 2021.
推荐语:利用深度符号回归,寻找拟合数据的最佳数学表达式。
Wassim Tenachi, et al. Deep symbolic regression for physics guided by units constraints: toward the automated discovery of physical laws.
arXiv:2303.03192 [astro-ph.IM]
Yang-Hui He,Minhyong Kim. Learning Algebraic Structures: Preliminary Investigations.
Yang-Hui He. Deep-Learning the Landscape.
推荐语: 利用神经网络,基于数学数据研究Calabi-Yau流形,向量丛,规范场论等。
Yang-Hui He . Machine-Learning Mathematical Structures.
Yang-Hui He , Vishnu Jejjala , Brent D. Nelson. hep-th.
推荐语: 利用arXiv部分科学论文与Word2Vector算法进行文本分析。
Eder C, Faugère, Jean Charles. A survey on signature-based Grobner basis computations. arXiv.1404.1774.
推荐语:论文讲述了基于签名的Grobner基算法的历史。基于签名的算法是Grobner基算法中的一个里程碑式的进步。该论文对该算法的进展进行了一次总结,得出了截止2014年该算法实质的进步和真正需要提升的方面。
Peifer D , Stillman M , Halpern-Leistner D. Learning selection strategies in Buchberger’s algorithm. arXiv.2005.01917.
推荐语:利用学习理论尝试优化Grobner基算法。
Lu, Dong & Wang, Dingkang & Xiao, Fanghui & Zheng, Xiaopeng. (2023). Signature-Based Standard Basis Algorithm Under the Framework of Gvw Algorithm. SSRN Electronic Journal. 10.2139/ssrn.4383360.
Dave Bayer, The division algorithm and the Hilbert scheme. Ph.D. Thesis, Harvard University, June 1982. 168 pages.
math.columbia.edu/~bayer/papers/Bayer-thesis.pdf
推荐语:Macaulay作者之一的Bayer的博士论文,是当代代数几何与除法算法理论相结合的开山之作。
Vlad, Raluca. 2022. A Discussion of Gröbner Bases and the Hilbert Scheme. Bachelor’s thesis, Harvard College. https://dash.harvard.edu/bitstream/handle/1/37371732/thesis.pdf?sequence=1
推荐语:非常适合快速了解Grobner基的基本概念和简单应用。
https://doc.sagemath.org/html/en/a_tour_of_sage/
SageMath是非常强大的开源数学软件,基于Python,可直接运行Python,十分全面。
https://docs.gap-system.org/doc/tut/chap0_mj.html
GAP是一款专门针对群论和线性代数的符号计算系统,基于C。
Macaulay2Doc —— Macaulay2 documentation
http://www2.macaulay2.com/Macaulay2/doc/Macaulay2/share/doc/Macaulay2/Macaulay2Doc/html/
Macaulay2是一款计算Grobner基的计算机代数系统,主要用于处理交换环及其模上的符号计算问题,是代数几何中常用的软件。
https://pari.math.u-bordeaux.fr/doc.html
Pari/GP是一款用来计算算术几何与代数数论、域扩张相关领域的代数系统。
https://maxima.sourceforge.io/docs/manual/maxima_toc.html
Maxima是一款常用的计算机代数系统,对标Mathematica, Maple等软件,是世界上最早的通用计算机代数系统。
数学是人工智能(AI)的灵魂,它不仅是AI发展的基础,也是其各个领域和应用的核心驱动力。从数据处理到模型优化,从算法设计到决策推断,数学在AI中扮演着多重角色,无处不在,不可或缺。
大模型与神经网络的成功离不开数学的关键贡献。范畴论为构建更抽象、通用的模型框架提供基础,帮助我们从更宏观的角度理解网络结构和操作。对比学习借助数学的距离度量和相似性概念,使模型能更准确地捕捉数据的关系。控制理论为优化算法提供指导,从微分方程到最优控制方法,有助于在参数空间中寻找最佳解。这些数学概念在大模型与神经网络的设计、训练和优化中发挥着不可或缺的作用,推动了人工智能领域的前沿研究和应用。
拓扑数据分析凭借数学的深远贡献在数据理解领域崭露头角。持续同调揭示数据的拓扑特征,通过对形状和连接性的量化,帮助揭示数据内部结构。拓扑机器学习融合了几何和代数的思想,将拓扑概念引入模型中,加深对数据的认知。而持续谱图法通过映射数据到特征空间,并分析其持续谱,提供了更丰富的数据表征,有助于发现数据中的模式和关系。这些数学工具共同促进了在复杂数据中的深入探索和发现,为数据分析注入了新的视角和能力。
图神经网络在数学的引导下取得突破性进展。消息传递范式运用线性代数与图论,将信息在图节点间传递,增强节点表示。突破GNN瓶颈需要深入图结构的数学洞察,控制理论和动态系统有助于解决动态图问题。在化学和细胞领域,图神经网络的数学建模从分子相互作用到蛋白质结构,为生命科学揭示新的见解。
总之,数学为AI的核心提供了坚实基础。大模型与神经网络的数学基础驱动着创新算法的发展。拓扑数据分析引领我们从数据中挖掘深层模式。图神经网络则将数学应用于更复杂的关系数据解析。这些数学领域共同推动AI领域的前进,开创出更广阔的可能性。
Yuan, Yang. “On the Power of Foundation Models.” Proceedings of the 40th International Conference on Machine Learning. Ed. Andreas, Krause, et al.s.: PMLR, 2023.
推荐语:本文使用范畴论,对预训练大模型的能力边界进行了理论刻画。
Kashiwara, Masaki, and Pierre Schapira. Categories and Sheaves. Springer Berlin, Heidelberg, 2006.
Riehl, Emily. Category Theory in Context. Courier Dover Publications, 2017. Print.
Radford, Alec, et al. “Improving Language Understanding by Generative Pre-Training.” (2018).
Chen, Ting, et al. “A simple framework for contrastive learning of visual representations.” International conference on machine learning. PMLR, 2020.
推荐语:预测相似图对的SimCLR算法,对于图像分类任务非常有效。
He, Kaiming, et al. “Masked autoencoders are scalable vision learners.” Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2022.
推荐语:基于遮挡预测的MAE算法,在各类图像下游任务中都有很好的表现。
Gidaris, Spyros, Praveer Singh, and Nikos Komodakis. “Unsupervised Representation Learning by Predicting Image Rotations.” arXiv preprint arXiv:1803.07728 (2018).
推荐语:基于旋转预测的算法,是非常简单而且早期的预训练算法。
Tan, Zhiquan, et al. “Contrastive Learning Is Spectral Clustering on Similarity Graph.” arXiv preprint arXiv:2303.15103 (2023).
https://arxiv.org/abs/2303.15103v2
推荐语:本文严格刻画了SimCLR与CLIP这两个常用预训练算法,证明其与相似图的谱聚类是等价的。该等价性并不平凡,它可以看作是《On the Power of Foundation Models》的一个最简单的例子,为米田嵌入在再生核希尔伯特空间的具体表现。
Van Assel, Hugues, et al. “A Probabilistic Graph Coupling View of Dimension Reduction.” Advances in Neural Information Processing Systems 35 (2022): 10696-708.
推荐语:本文提出了分析SimCLR/CLIP使用的理论框架
Fan, Lijie, et al. “Improving Clip Training with Language Rewrites.” arXiv preprint arXiv:2305.20088 (2023).
https://arxiv.org/pdf/2305.20088.pdf
推荐语:本文是改进CLIP的最新工作,背后的基础原理可以由同样的理论框架解释,有很好的效果。
HaoChen, Jeff Z, et al. “Provable Guarantees for Self-Supervised Deep Learning with Spectral Contrastive Loss.” Advances in Neural Information Processing Systems 34 (2021): 5000-11.
https://arxiv.org/pdf/2106.04156.pdf
推荐语:本文是首篇分析SimCLR(变体)的理论工作,突破性地提出了在Population分布中分析算法,证明了SimCLR变体在做某种谱聚类(变体)。
Radford, Alec, et al. “Learning transferable visual models from natural language supervision.” International conference on machine learning. PMLR, 2021.
推荐语:连接图像与文字的CLIP算法,是Dall-E/EVA/MILAN等多模态模型的重要组成部分。
-
最大化原理视角下的神经网络训练过程、深度学习中的平均场最优控制建模:
Li, Qianxiao, Long Chen, and Cheng Tai. “Maximum Principle Based Algorithms for Deep Learning.” arXiv preprint arXiv:1710.09513 (2017).
推荐语:本研究讨论了如何用现代控制理论中的庞特里亚金最大原理对深度神经网络的优化过程进行建模。
E, Weinan, Jiequn Han, and Qianxiao Li. “A Mean-Field Optimal Control Formulation of Deep Learning.” Research in the Mathematical Sciences 6.1 (2018): 10.
推荐语:本研究介绍了深度学习中群体风险最小化问题作为均值场最优控制问题的数学表述,陈述并证明了哈密尔顿-雅可比-贝尔曼类型和庞特里亚金类型的最优条件。这些平均场结果反映了学习问题的概率性质。
Edelsbrunner, Herbert, and John Harer. “Persistent Homology-a Survey.” Contemporary mathematics 453.26 (2008): 257-82.
推荐语:持续同调(Persistent Homology)是拓扑数据处理(Topological data analysis: TDA)核心模型。
Tauzin, Guillaume, et al. “giotto-tda: A topological data analysis toolkit for machine learning and data exploration.” The Journal of Machine Learning Research 22.1 (2021): 1834-1839.
推荐语:这这篇文章总结了拓扑数据和机器学习的结合的相关理论。
Cang, Zixuan, Lin Mu, and Guo-Wei Wei. “Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening.” PLoS computational biology 14.1 (2018): e1005929.
Wang, Menglun, Zixuan Cang, and Guo-Wei Wei. “A topology-based network tree for the prediction of protein–protein binding affinity changes following mutation.” Nature Machine Intelligence 2.2 (2020): 116-123.
推荐语:拓扑机器学习模型预测蛋白质突变结合能改变量。
Nguyen, Duc Duy, et al. “MathDL: mathematical deep learning for D3R Grand Challenge 4.” Journal of computer-aided molecular design 34 (2020): 131-147.
Wang, Rui, Duc Duy Nguyen, and Guo‐Wei Wei. “Persistent Spectral Graph.” International journal for numerical methods in biomedical engineering 36.9 (2020): e3376.
Zomorodian, Afra J. Topology for Computing. Vol. 16: Cambridge university press, 2005.
Otter, Nina, et al. “A Roadmap for the Computation of Persistent Homology.” EPJ Data Science 6 (2017): 1-38.
Zomorodian, Afra, and Gunnar Carlsson. “Computing persistent homology.” Proceedings of the twentieth annual symposium on Computational geometry. 2004.
Pun, Chi Seng, Si Xian Lee, and Kelin Xia. “Persistent-Homology-Based Machine Learning: A Survey and a Comparative Study.” Artificial Intelligence Review 55.7 (2022): 5169-213.
Nguyen, Duc Duy, Zixuan Cang, and Guo-Wei Wei. “A Review of Mathematical Representations of Biomolecular Data.” Physical Chemistry Chemical Physics 22.8 (2020): 4343-67.
Chen, Jiahui, et al. “Mutations Strengthened Sars-Cov-2 Infectivity.” Journal of molecular biology 432.19 (2020): 5212-26.
Meng, Zhenyu, and Kelin Xia. “Persistent spectral–based machine learning (PerSpect ML) for protein-ligand binding affinity prediction.” Science advances 7.19 (2021): eabc5329.
Mémoli, Facundo, Zhengchao Wan, and Yusu Wang. “Persistent Laplacians: Properties, algorithms and implications.” SIAM Journal on Mathematics of Data Science 4.2 (2022): 858-884.
Gilmer, Justin, et al. “Neural message passing for quantum chemistry.” International conference on machine learning. PMLR, 2017.
推荐语:本文作为图神经网络中的一个里程碑之作,提出了消息传递范式,从而将主流的图神经网络模型都纳入到这一范式之中,为未来对图神经网络的理论研究提供一个框架。此外本文使用QM9验证了基于消息传递范式所设计的图神经网络在量子化学性质预测上的性能。
Schütt, Kristof T, et al. “Schnet–a Deep Learning Architecture for Molecules and Materials.” The Journal of Chemical Physics 148.24 (2018).
推荐语:本文作为深度学习在化学性质计算方面的深度应用,并提供了一个完整的针对量子化学计算的开源框架。
Xu, Keyulu, et al. “How Powerful Are Graph Neural Networks?” arXiv preprint arXiv:1810.00826 (2018).
推荐语:这篇文章从理论上分析了GNN的表达能力的上限,为之后GNN的瓶颈突破提供了一个理论方向。
Ebli, Stefania, Michaël Defferrard, and Gard Spreemann. “Simplicial Neural Networks.” arXiv preprint arXiv:2010.03633 (2020).
推荐语:本文引入了单纯复形作为图数据的更一般化形式,此外设计了卷积操作并在此基础上构建模型。
Bodnar, Cristian, et al. “Weisfeiler and lehman go topological: Message passing simplicial networks.” International Conference on Machine Learning. PMLR, 2021.
推荐语:通过引入单纯形的概念,来突破GNN收到的WL-test的限制。
Bodnar, Cristian, et al. “Weisfeiler and Lehman Go Cellular: Cw Networks.” Advances in Neural Information Processing Systems 34 (2021): 2625-40.
推荐语:基于2阶单纯形对应的是三角形,从而难以对苯环等含有超过3个原子构成的分子环状结构进行有效的处理,因此引入了元胞复形对单纯复形的消息传递网络进行泛化,使其更加适用于化学性质预测任务。
Jiang, Yi, et al. “Topological Representations of Crystalline Compounds for the Machine-Learning Prediction of Materials Properties.” npj computational materials 7.1 (2021): 28.
推荐语:本文通过引入一种基于拓扑学的原子特异性持久同调(ASPH)方法,解决了如何为晶体化合物等复杂数据集构建具有化学洞察力的低维表示的问题,并且开发了一个高度准确的机器学习模型,用于预测晶体化合物的形成能。
Bodnar, Cristian, et al. “Neural sheaf diffusion: A topological perspective on heterophily and oversmoothing in gnns.” Advances in Neural Information Processing Systems 35 (2022): 18527-18541.
推荐语:本文提出了一种基于细胞层级结构的扩散过程Sheaf Diffusion,可以在无限时间极限下处理越来越复杂的节点分类任务,以解决图神经网络中的异质性和过度平滑问题,此外证明了其比Graph Convolutional Networks更加灵活,对渐近行为具有更大的控制能力。
Qiao, Zhuoran, et al. “Informing Geometric Deep Learning with Electronic Interactions to Accelerate Quantum Chemistry.” Proceedings of the National Academy of Sciences 119.31 (2022): e2205221119.
推荐语:本文提出了一种名为OrbNet-Equi的新方法,使用受物理启发的神经网络来学习基于原子轨道之间的电子相互作用的分子表示,以解释如何利用电子相互作用来加速量子化学计算的问题,并且证明比传统的机器学习方法和密度泛函理论更准确和更快。
Fu, Xiang, et al. “Simulate Time-Integrated Coarse-Grained Molecular Dynamics with Geometric Machine Learning.” arXiv preprint arXiv:2204.10348 (2022).
推荐语:本文提出了一种基于机器学习的方法,结合粗粒化和时间积分建模与图神经网络,用于模拟分子动力学,该模型优于基于GNN和长短期记忆(LSTM)神经网络架构的两个监督学习基准模型。与传统力场相比,该模型可以在需要长时间模拟的估计问题中提供几个数量级的加速。通过模拟隐式溶剂中的单链粗粒化聚合物,并可靠地估计需要长时间模拟的聚合物性质,证明了该模型的性能。
https://pattern.swarma.org/study_group_issue/484
Xu, Hao, et al. “Retention time prediction for chromatographic enantioseparation by quantile geometry-enhanced graph neural network.” Nature Communications 14.1 (2023): 3095.
推荐语:本文提出的研究框架使用机器学习技术改进色谱手性分离的效率。该框架解决了数据获取、手性分子的三维表示和数据不确定性等问题。它通过从现有文献中提取实验结果构建了一个手性分子保留时间数据集,并使用一种专门的图神经网络(QGeoGNN)进行预测。QGeoGNN在单柱和多柱预测中准确预测了手性分子的保留时间,以及在不同条件下的分离概率。然而,数据的代表性和质量、数据的不确定性、低相似性分子的预测准确性以及特征提取过程存在一定的限制。尽管存在这些限制,该框架在色谱手性分离中确定适当实验条件方面具有重要潜力。