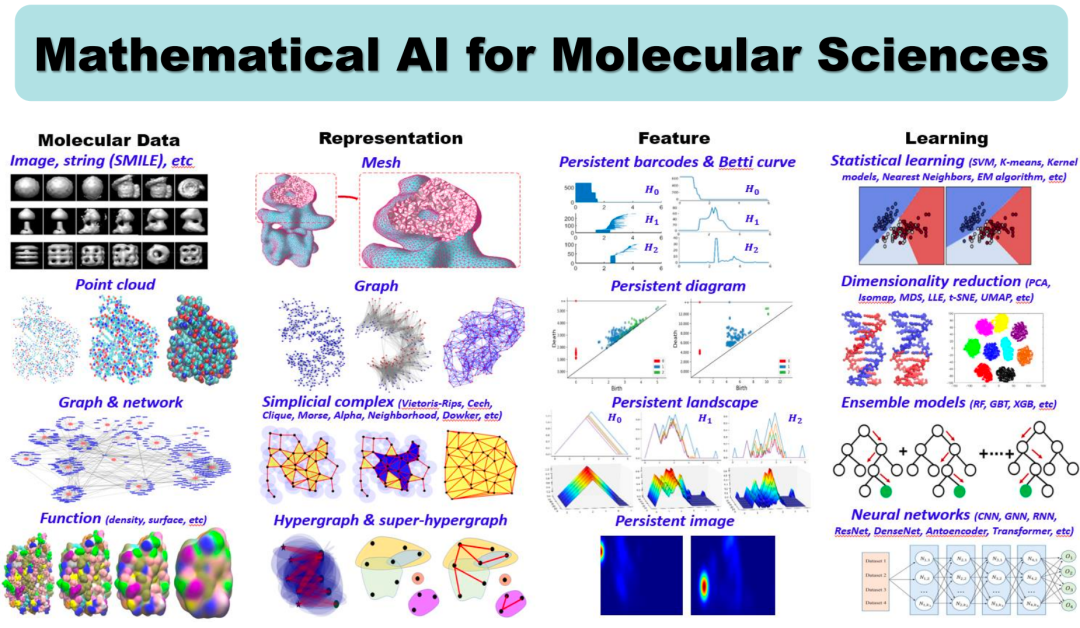
本文以分子数据处理为切入点,探讨拓扑数据分析(Topological Data Analysis, TDA)的应用和特点。AI 在数据处理上的两个关键环节——数据表征和建模分析特性,与拓扑数据分析有着紧密的联系。接下来,我们将展开介绍这两个环节。
Tauzin, Guillaume, et al. “giotto-tda: A topological data analysis toolkit for machine learning and data exploration.” The Journal of Machine Learning Research 22.1 (2021): 1834-1839.
Chazal, Frédéric, and Bertrand Michel. “An introduction to topological data analysis: fundamental and practical aspects for data scientists.” Frontiers in artificial intelligence 4 (2021): 108.
在处理图像数据时,我们可以借助神经网络模型生成相应的数据表示。例如通过提取特定的特征点构建网格模型进行人脸识别。除了网格模型,还有其他如特征图和热度图等不同的数据表示方式。虽然源自同一图像数据,但从数学角度可以建立起不同的模型:最简单的矩阵模型,或者点阵模型、网格模型,甚至更复杂的函数模型。一旦数学模型建立,就可以基于模型提取特征,并与后续关注的信息产生联系,如通过多层感知器(MLP)进行预测等。
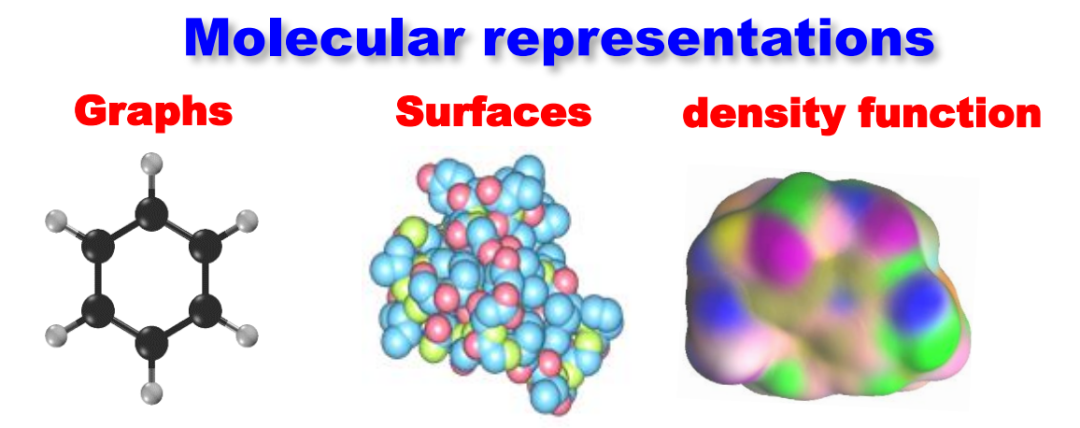
类似地,在处理分子数据(如小分子数据和蛋白质数据)时,也有多种不同的数据表示方式。一种常见方法是基于共价键的图表征,其中每个节点代表一个原子,边代表共价键,形成一种图的表示形式。
除此之外,还有几何方法,例如将原子看作半径固定的球体,观察者可以从球体集合的外部,即分子的表面进行研究,查看其表面积或凸凹区域。这些凸凹区域与原子间的相互作用信息有关,这种描述更偏向几何。
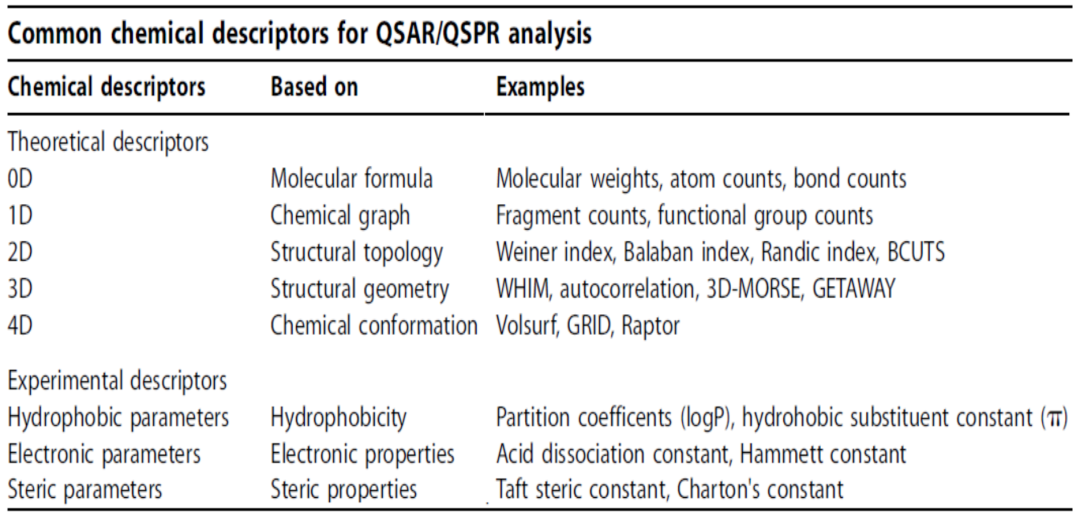
更进一步,还可以通过密度泛函理论来计算电子密度或电子函数分布,将分子数据转化为一种空间形态的数据表现形式。因此,尽管源自同样的分子数据,我们可以从多个角度对其进行表征。一旦完成表征,就可以在此基础上提取各种特性,包括各种指纹(fingerprint)和描述符(descriptor)等等。这些性质可能和最终想要理解的功能产生联系,例如水溶性、脂溶性、毒性等。
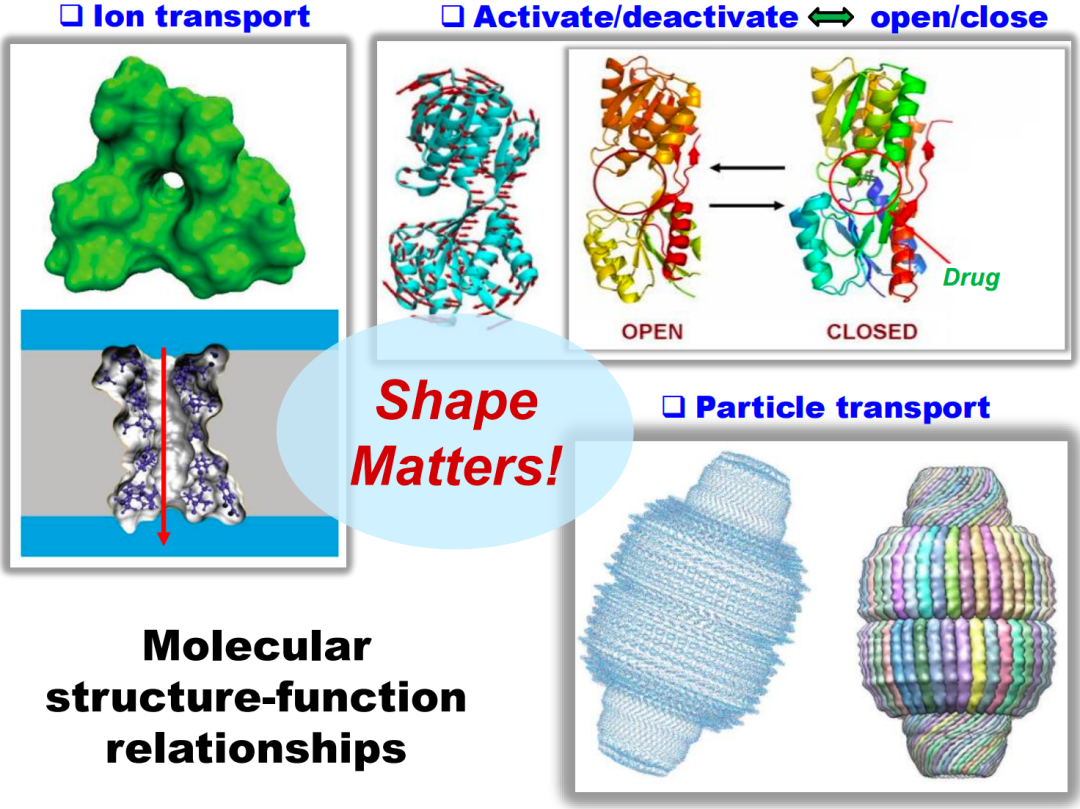
在构建关于分子功能模型的过程中,大量使用了结构数据。这是因为分子的结构和其功能之间存在强烈的关系,被称为“结构-功能关系”(Structure-Function Relationship)。
例如,离子通道蛋白质的显著特点是它们中心有一个洞(图4左上),这个洞对离子通道的功能至关重要,因为它方便了细胞膜外部的离子进入膜内,或者膜内的离子离开细胞。另一个例子是蛋白质笼(图4右下),这种蛋白质的表面有一定结构,但其内部是空的,就像用来装东西的盒子,这种空心的结构有利于某些物质的存储和运输。最后一个例子是具有两个固定区域,并通过一个灵活连接区域相连的分子。这种结构可以形成一种开关状态,使得分子能够处于激发态或非激发态,从而影响其功能。
无论是通过共价键连接还是通过非共价键的相互作用,都会影响最终的稳定态结构,这种稳定态结构与分子功能紧密相关。因此,描述分子的结构对于理解分子功能具有重要作用。为更好地描绘分子的结构,大量的描述符(无论是组合量,代数量还是几何量)被提取了出来。在这些描述符中,有一些关注拓扑特性,比如图上向量、几何量等等,还有一些关注组合或邻近信息的指纹。
在大量关于结构的描述量中,可能存在某些更本质、更全局的量,它们能够更好地抓住结构的整体信息,从而在理解和描绘分子的功能方面起到更重要的作用。这就引出了拓扑数据处理的核心:通过拓扑不变量来描述数据。
拓扑数据分析与传统的工具相比有三个主要特征:
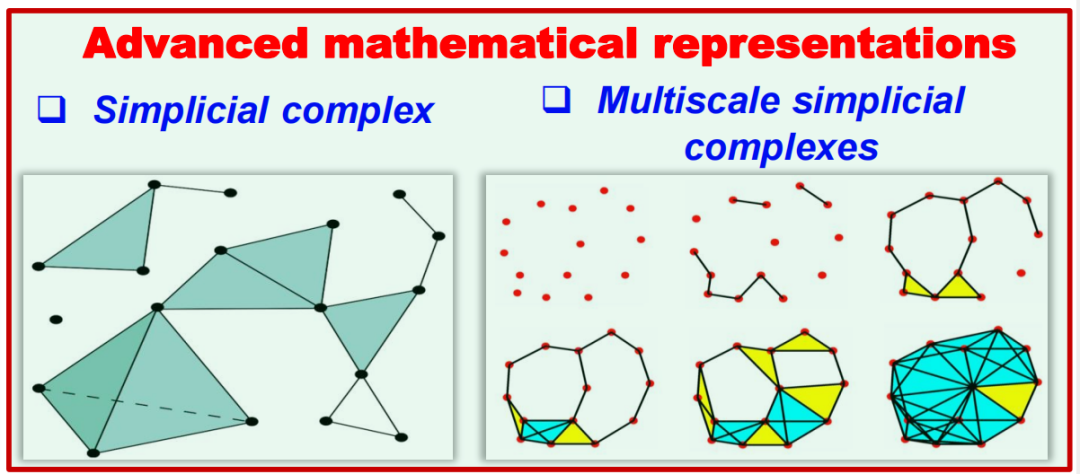
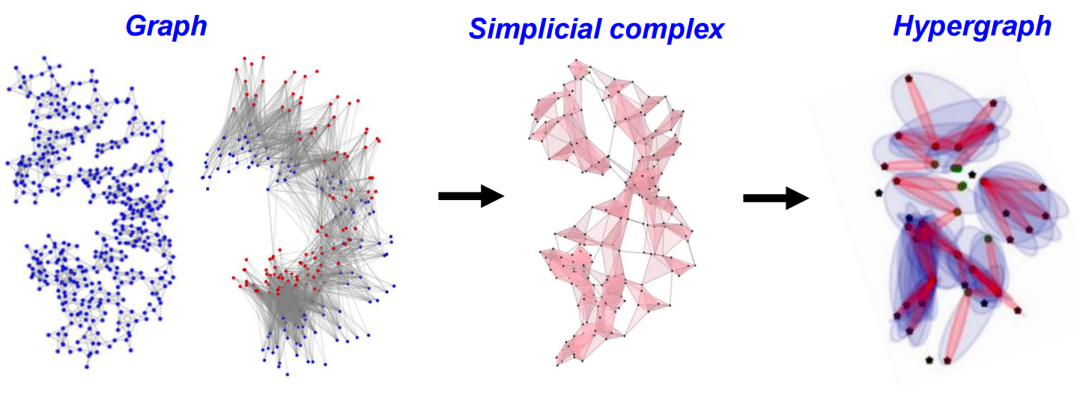
1)单纯复形:采用单纯复形(simplicial complex)的描述方式,相比图描述能捕获数据中更丰富的拓扑和几何信息。
2)拓扑不变量:拓扑数据分析使用拓扑不变量,而非仅仅依赖于统计量或描述性量。这些拓扑不变量可以提供对数据的深度理解,包括数据的连接性、洞等复杂结构。
3)过滤流过程:拓扑数据分析包含一个过滤流过程,这个过滤流过程可以与系统内的多尺度描述很好地结合。通过从不同的尺度去观察和分析数据,我们能够得到更全面的信息。
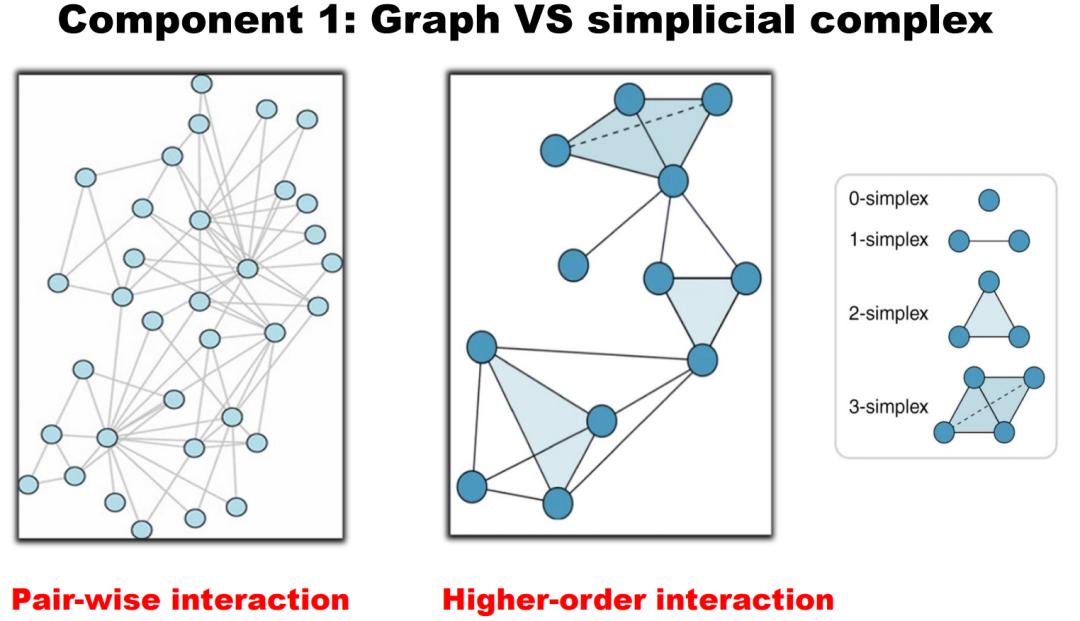
在非数学领域,如计算机科学、工程和生物学中,人们通常使用图来表达实体之间的连接关系。然而,在基础数学领域中,更经常使用的是称为单纯复形(Simplicial Complex)的描述方式。作为高级的拓扑工具,单纯复形能更好地描绘复杂系统中的结构信息。
1)高维度描绘:除表示节点和边(即0维和1维的对象),单纯复形可以表示更高维度的对象。例如,填充的三角形代表一个2维的对象,填充的四面体代表3维对象。
2)高阶相互作用:图主要描述两两之间的相互作用,而通过引入“更高维度的单元”,单纯复形能够表达出超过两个实体之间的相互作用。例如,填充的三角形表示三个实体之间的相互作用,填充的四面体表示四个实体之间的相互作用。注意二者的区别,用一个形象的比喻来解释:图可以表示父亲与孩子的关系,以及母亲与孩子的关系;而复形则能表示父亲、母亲、孩子三者组成的家庭单位的关系,用一个填充的二维三角形。
3)距离和体积的描述:图通常只能描述路径或距离,单纯复形则可以描述面积,两边夹角(2维单元)或者体积(3维单元)。这为我们提供了更高阶的信息,使我们能够捕获到实体间更复杂的相互作用。
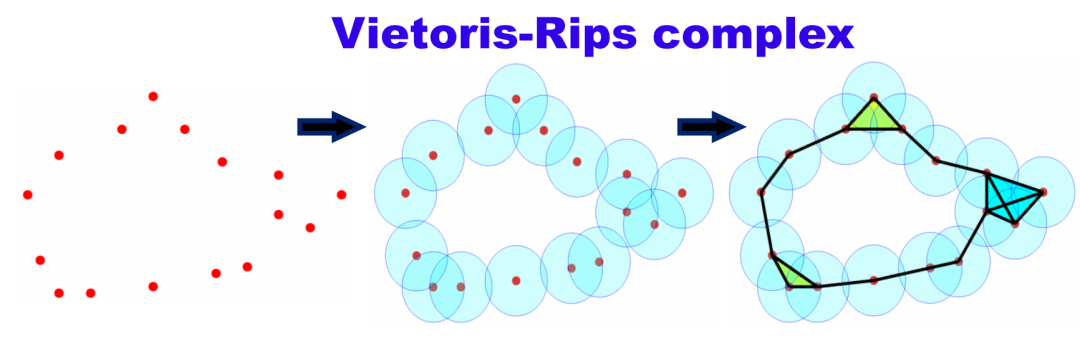
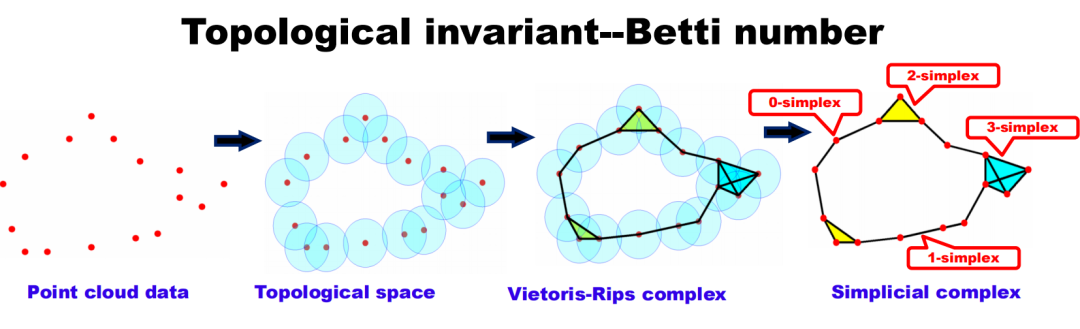
举个简单的例子,从一组点和固定距离构造一个复形(Vietoris-Rips复形):
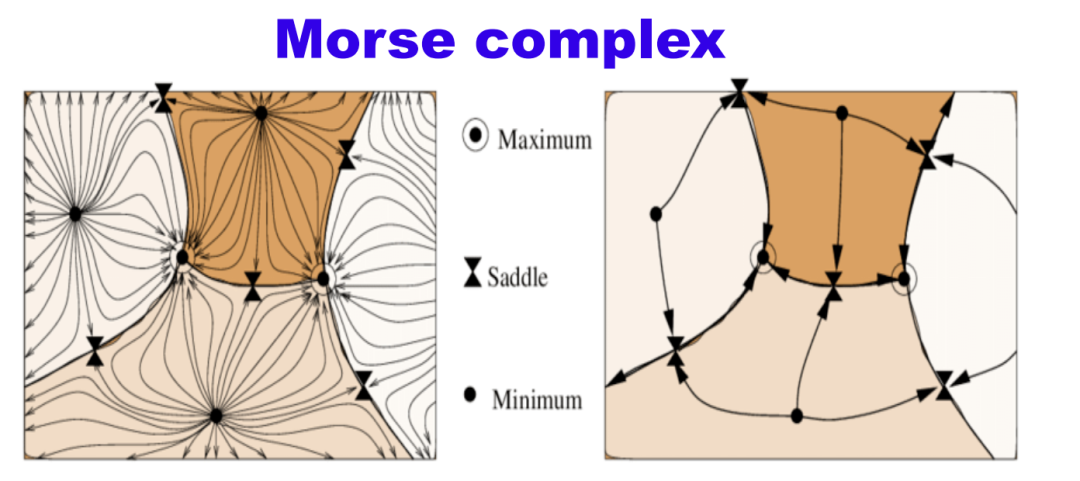
或者复杂些,在微分拓扑中,根据函数导数取值0的信息及其正定性将流形分片(Morse复形):
Magillo, Paola, et al. “A discrete approach to compute terrain morphology.” Computer Vision and Computer Graphics. Theory and Applications: International Conference VISIGRAPP 2007, Barcelona, Spain, March 8-11, 2007. Revised Selected Papers. Springer Berlin Heidelberg, 2008.
提取 Morse 复形的离散方法
拓扑不变量是对拓扑空间性质的一种刻画,在数据分析中提供了全局和本质的视角。相较于如 PCA 这样的统计方法,它更关注整体的性质。举两个经典的拓扑不变量例子:
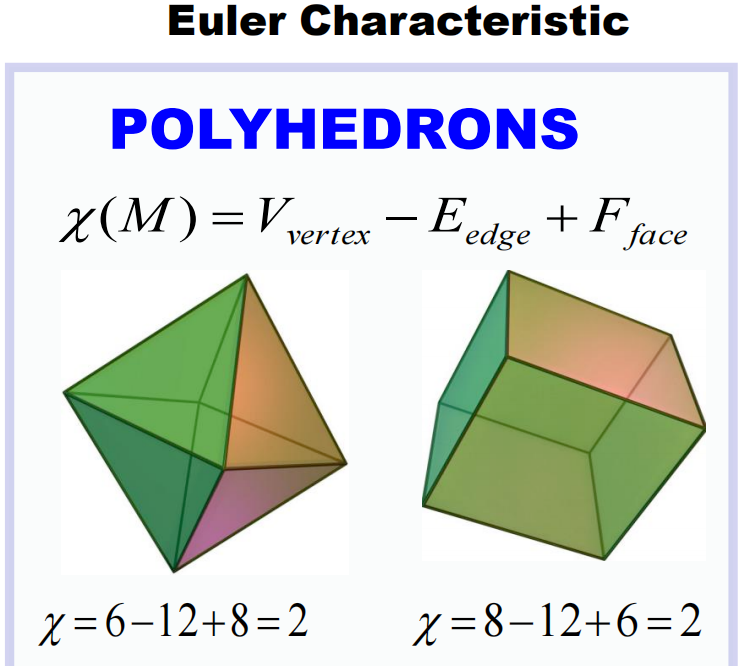
1)欧拉示性数:欧拉示性数取值为“顶点数 减去 边数 加上 面数”(V-E+F)。对于拓扑等价于球体的多面体(例如立方体或八面体等),欧拉示性数均为2。这是因为在拓扑意义上,这些形状都可以被连续地变形为球形。
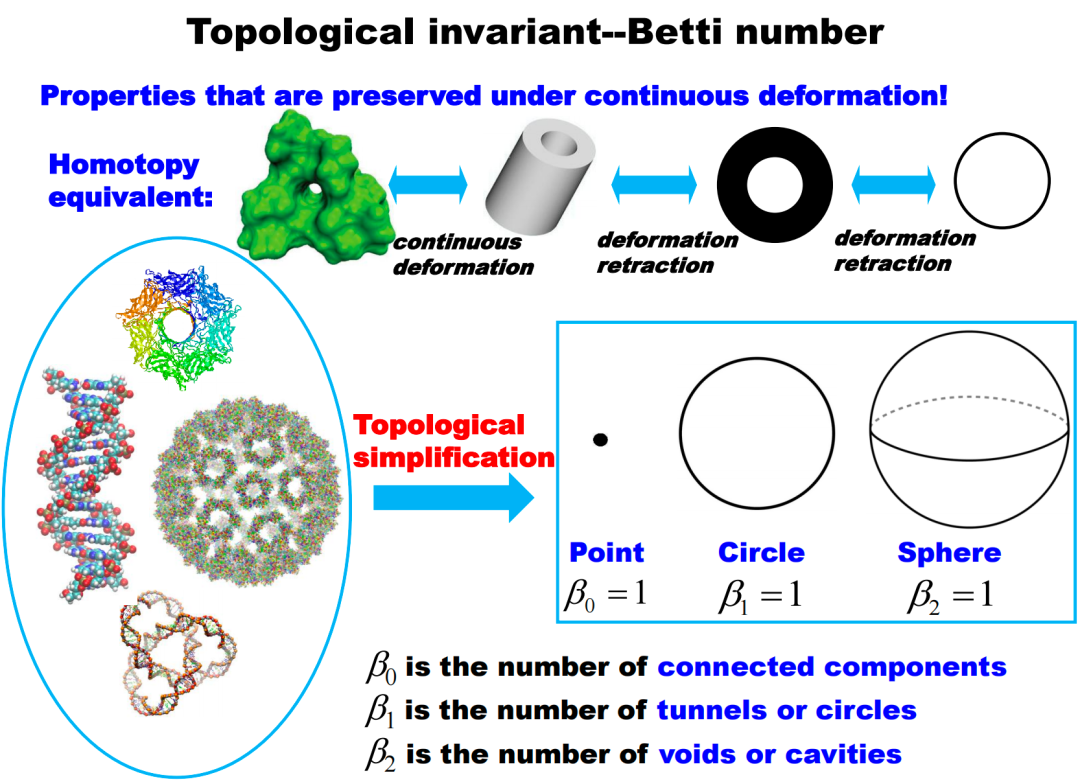
2)贝蒂数:贝蒂数是在拓扑数据分析(TDA)中常用的拓扑不变量,用来描述拓扑空间的复杂度。零维的贝蒂数表示连通分支的数量,一维贝蒂数表示独立环路的数量,二维贝蒂数表示“空心”球面的数量,等等。
过滤流过程(filtration)是拓扑数据分析的核心概念。这个过程可以理解为不断改变尺度以观察复杂系统如何随着尺度的变化而变化。过滤流过程在不同的尺度上描述单纯复形,并且生成相应的条形码来记录每个尺度下的拓扑信息。
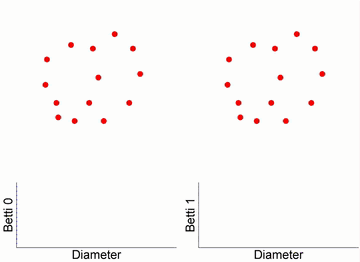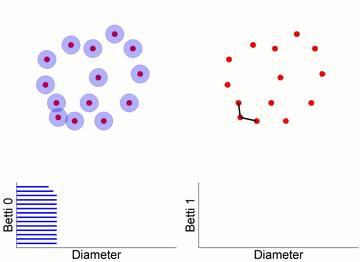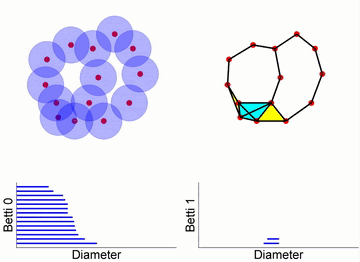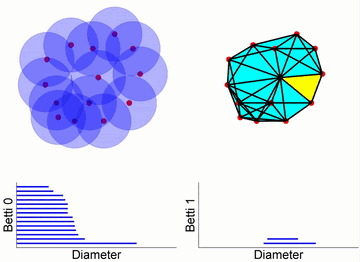
上图最左边的十四个点代表原始数据,每点周围有一个球体,随时间推移,这些球体的半径增大。当两个球体接触时,表示两个数据点之间存在连接,这就形成了一条边,同时独立分支的数量减一。在过滤流过程中,随着球体半径的增大,独立元素逐渐减少,同时出现新的拓扑结构(比如环和更高维的洞)。
从图中的条形码可以看出,初始有14个独立节点,所以 Betti0 为 14 个。随着时间的推移,球体之间的连接增多,独立的节点数目减少。同时,当出现闭合的路径时,就形成了环,可以在 Betti1 的条形码中看到这种变化。
图12. Vietoris-Rips 复形与单纯复形
通过过滤流过程和单纯复形,我们可以从全局和多尺度的角度理解复杂系统的结构,并通过 Betti 数这类拓扑不变量来量化这些性质。这种方法在机器学习、迁移学习等领域有着重要的应用,相比传统的统计工具,它提供了对数据深层本质结构的理解。
前边更多是从数学角度出发的讨论,在处理真实世界的问题时,我们该如何将拓扑理论应用到化学分子等具体科学问题上?以碳60分子为例,C60 是由 60 个碳原子组成的分子,其形状类似于足球,包含了 12 个五元环和 20 个六元环。
如下图所示,我们用拓扑数据分析进行分析,X 轴表示直径。
图14. C60 分子模型随直径变化的 Betti 数
• 在 Betti-0 中,有 60个条形码,其中 30 个较短,30 个较长。较短的代表碳碳双键,因为双键较强,原子拉得近;而较长的则代表碳碳单键,比双键要弱,因此距离稍长。这样,Betti-0 描述的是共价键的信息。
• 在 Betti-1 中,有 32 个条形码,其中 12 个较短,20 个较长。较短的对应五元环,而较长的则对应六元环。所以,Betti-1 描述的是环的信息。
• 在 Betti-2 中,可以看到一个长条形码,这个对应 C60 分子整体的空心结构。
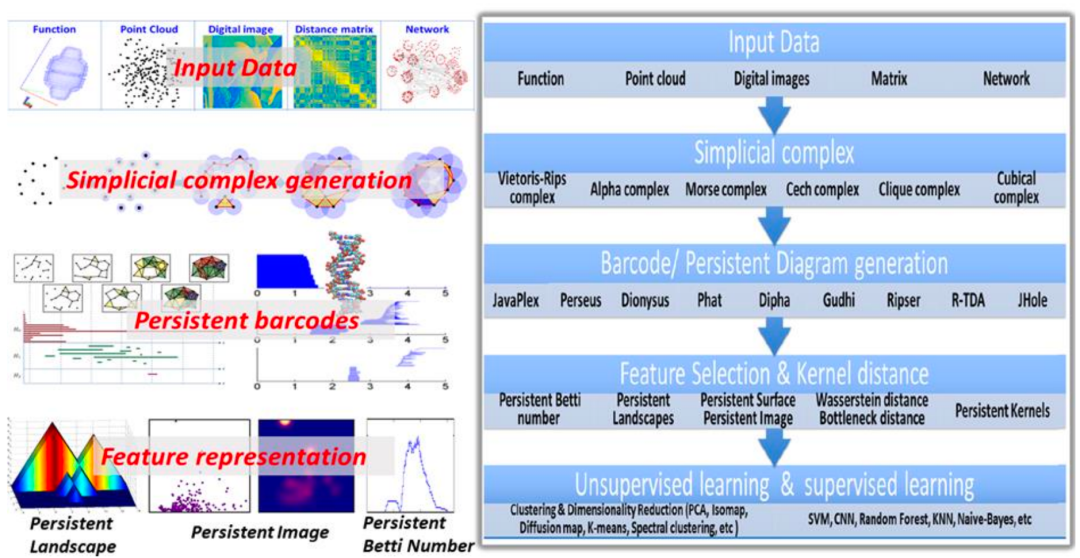
通过这些特征信息,我们将拓扑数据分析与机器学习相结合。例如在数据上构建不同类型的单纯复形,进行过滤流过程,得到条形码,然后提取各种特征(如最长的条形码、最短的条形码、总的数量等),并将这些特征输入到机器学习模型,如 Random Forest 或 Gradient Boosting Tree 等,进行功能预测等任务。这样就实现了拓扑深度学习的基本流程。
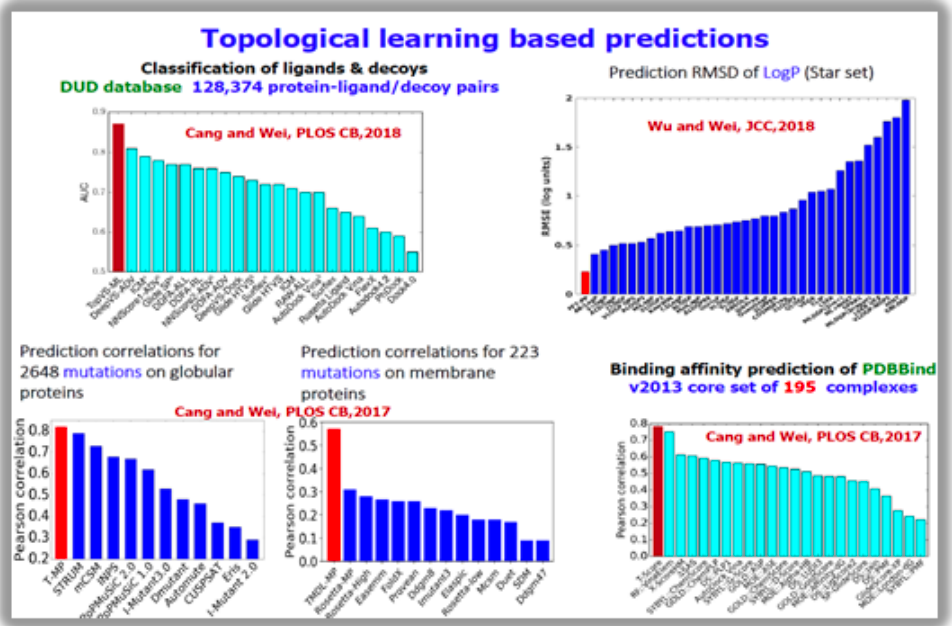
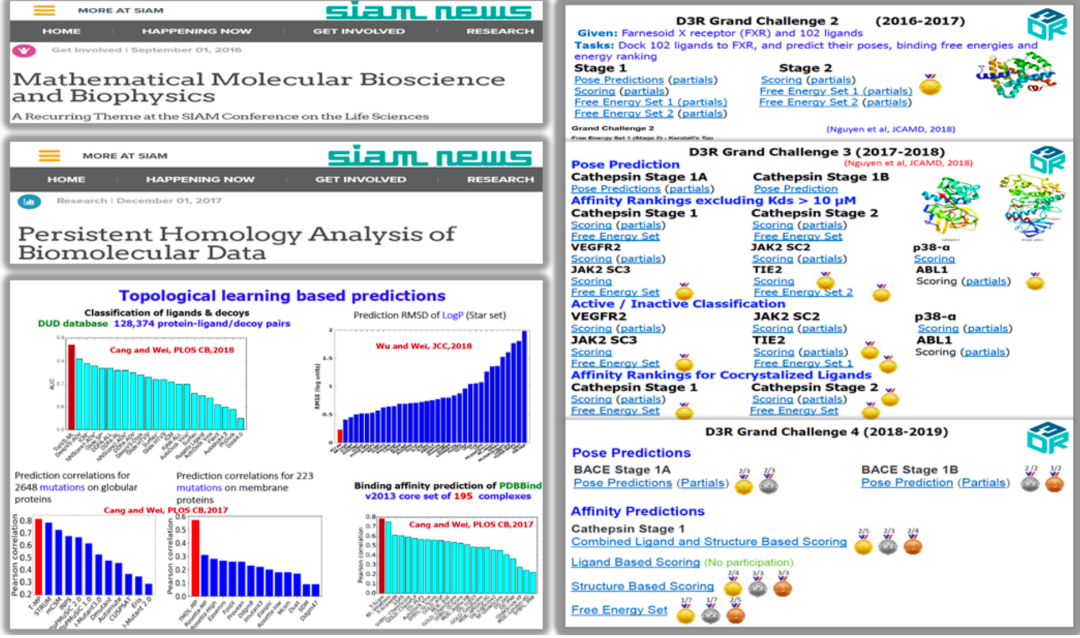
在拓扑数据分析(TDA)与机器学习相结合的研究领域中,魏国卫教授和他的团队做了大量的创新性工作。他们通过 TDA 提取数据集的特征,并将这些特征用于各种预测任务。在过去的几年里,在图网络并未广泛应用、且可处理数据量相对较小(通常在三千到四千之间)的时代,他们的研究成果表明 TDA 能提取出比传统统计方法或某些特定组合更有效的特征。
从多个benchmark数据集的结果来看,他们的基于 TDA 的模型表现非常好。尤其值得注意的是,他们在 D3R 药物设计比赛中,通过结合TDA和机器学习的方法,在2017和2018两届比赛中都取得了显著的优势,并超越了许多传统的方法。他们在TDA和机器学习结合的研究方向上的早期工作,为该领域奠定了坚实的基础。
Cang, Zixuan, Lin Mu, and Guo-Wei Wei. “Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening.” PLoS computational biology 14.1 (2018): e1005929.
拓扑机器学习模型预测配体蛋白质结合能。
Nguyen, Duc Duy, et al. “MathDL: mathematical deep learning for D3R Grand Challenge 4.” Journal of computer-aided molecular design 34 (2020): 131-147.
拓扑机器学习模型应用于药物设计。
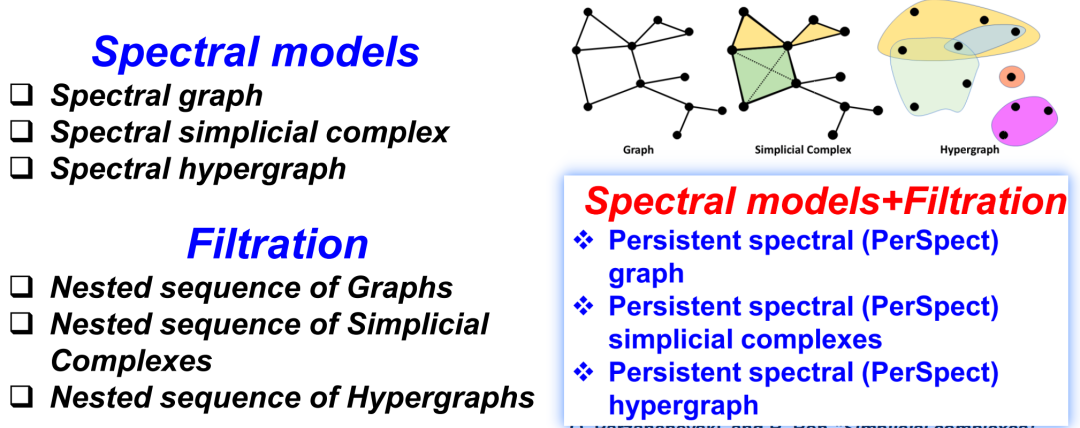
3.3 Persistent Spectral:谱图法结合过滤流过程
在观察和分析数据时,主要有两种方式:一是考虑数据的表征(representation),二是利用数据的特性(features)。前面讨论我们主要关注拓扑的特性,包括各种拓扑不变量,它们描述了结构的复杂性。另一方面,当我们想保留数据的更精细的特征,就需要考虑数据的其他数学不变量。例如,针对图或单纯复形,我们可以考虑谱图方法以及它的扩展,这种方法基于图、单纯复形或超图上的离散拉普拉斯算子(Hodge Laplacian),并用其谱的信息进行数据表示。
为将这两种思路相结合,我们提出一种新的模型 Persistent Spectral。这个模型综合利用了过滤流过程和谱图方法,在保留数据原始形态的同时,还能揭示其内在的拓扑特性。
Edelsbrunner, Herbert, and John Harer. “Persistent Homology-a Survey.” Contemporary mathematics 453.26 (2008): 257-82.
持续同调(Persistent Homology)是拓扑数据处理(Topological data analysis, TDA)核心模型。
Wang, Rui, Duc Duy Nguyen, and Guo‐Wei Wei. “Persistent Spectral Graph.” International journal for numerical methods in biomedical engineering 36.9 (2020): e3376.
提出了持续谱图法。
拉普拉斯矩阵
拉普拉斯矩阵的概念我们只做大致介绍,k 维拉普拉斯矩阵 Lk 有如下计算公式
举个例子,0维拉普拉斯矩阵 L0 以点为单位对象,对角线为点的度数,当点 i 和 j 连接时 L0 的 (i, j) 位置取 -1 否则取0。类似地,在复形上,将边作成单位对象,由边的关系得到 1 维拉普拉斯矩阵 L1 。
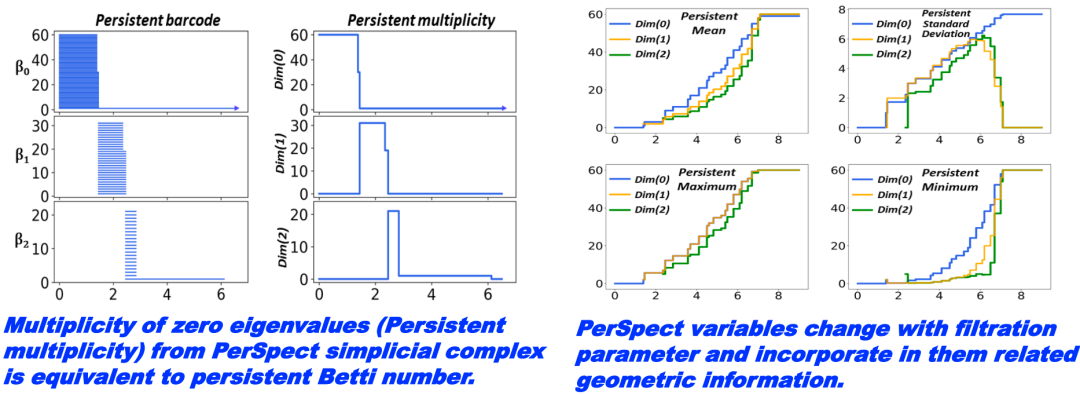
将得到拉普拉斯矩阵进行特征值分解,其中零特征值的数目对应了 Betti0,其反映图的连通分量的数量。拉普拉斯矩阵的非零特征值也包含有丰富的信息。比如最小的非零特征值,也被称为 Fiedler 值,常用来刻画图的连通性,展示单纯复形各部分之间的连接关系。
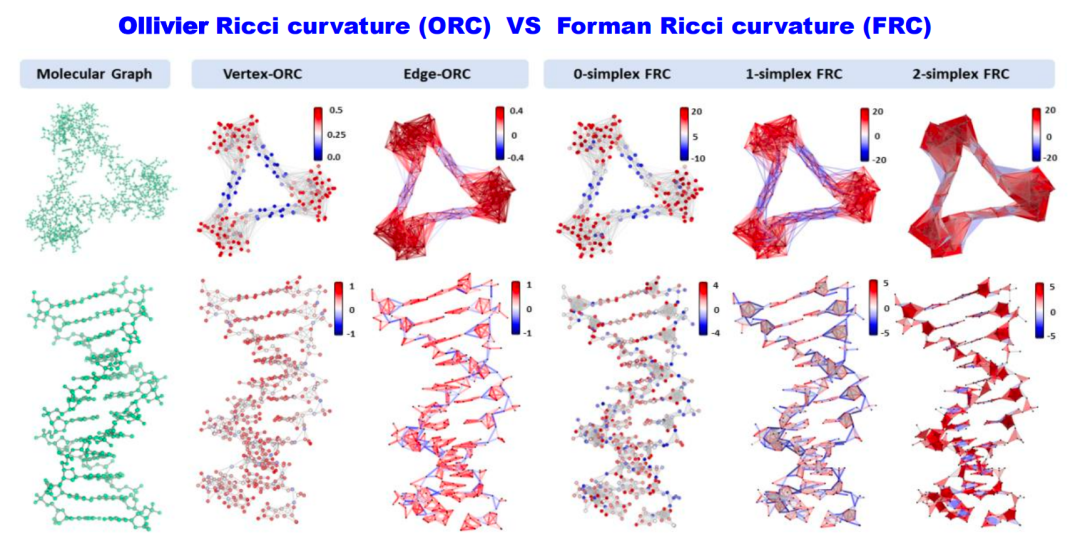
另外一个重要的不变量是几何不变量,例如 Ricci 曲率。Ricci 曲率能够捕获图或网络中的社区结构或簇(cluster)结构。举个例子,当图中有一个紧密连接的社区或聚类时,这个区域的 Ricci 曲率通常是一个较大的正值。而连接两个不同社区或聚类的桥梁部分,Ricci 曲率则可能为负值。因此,许多研究者利用 Ricci 曲率的赋值方法来描述网络中各区域之间的相互连接性。
Ricci 曲率及其它各种曲率都是用来描述整体结构、簇结构、社区结构以及链接结构间关系的重要工具,能用于揭示网络或数据集内部丰富复杂的拓扑和几何属性。
实际上,上边提到的信息可以相互关联起来。比如,拓扑学中的 Betti 数(homology信息)和Hodge Laplacian中的零特征值是一一对应的。离散形式的 Ricci 曲率(例如Forman Ricci curvature)也可以通过与Hodge Laplacian的某种组合(比如Bochner-Weitzenböck公式)来产生联系。

使用这些工具从不同角度描述数据的结构:
• Ricci 曲率帮助我们理解数据的几何性质;
• Betti 数或者更一般的 homology 信息揭示数据的拓扑性质;
3.5 单纯复形的构造
上边主要介绍几种基于数学不变量的数据的特征(featurization),包括 Betti数、曲率和谱信息等方式。另一个更本质的问题是数据的表征(representation)。比如用图、单纯复形,以及超图来表征数据。
考虑图或单纯复形的子结构,比如社区、簇或模块等。这些子结构往往能够展示数据内部更加精细的组织形式,从而帮助我们更准确地理解和预测系统的行为。此外,也可以考虑动态的视角,比如时间演化网络,这种视角可以帮助我们理解系统的变化和发展规律。
构造单纯复形的方法很多,除了常用的方法如 Clique complex,VR complex,Alpha complex,等等,下边会介绍三种方法。他们在拓扑学中有着广泛应用。另外拓扑信息还可以通过其他代数模型来表征,这里我们将介绍一种特殊的代数模型,Tor-algebra。
Bodnar, Cristian. “Topological deep learning: graphs, complexes, sheaves.” PhD diss., University of Cambridge, 2022.
3.5.1 Neighborhood Complex
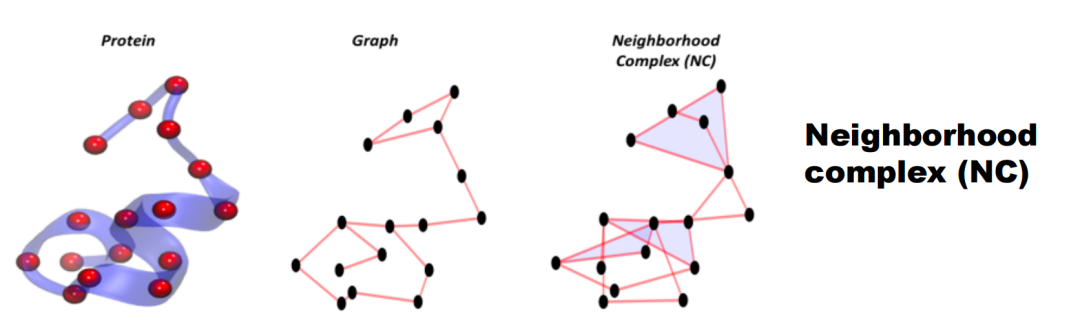
最简单的构造方式是邻域复形(Neighborhood Complex),基于给定图中的邻接关系来构建。如下图所示,假设有一个点,其邻接点有三个。我们将这四个点构成一个四边形(称为2-simplex)。如果邻接点中有两点也相互邻接,则连起这两个点构成一条边(1-simplex)。如果有三点相互邻接,那么将这三点组成一个填充的三角形(2-simplex)。通过这种方式将图转化为邻域复形。
这种邻域复形所描述的拓扑信息与由其他方式(例如Clique Complex)所得到的结果会有显著的不同。
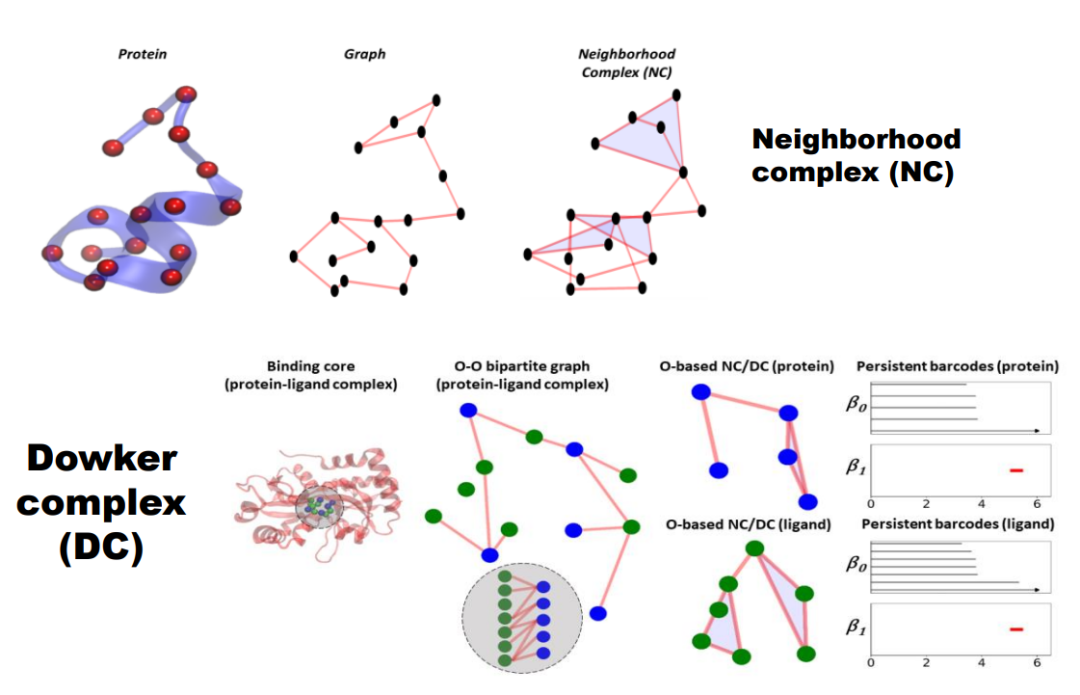
另外一个有趣的单纯复形构造方式是 Dowker Complex。
当研究两个实体间的相互作用,例如两个分子之间的连接时,我们可能更关心分子之间的全局交互关系,而不是各自内部的连接方式。此时二部图(bipartite graph)是一个很好的工具,我们将小分子(例如蓝点和绿点)视为图节点,再根据它们之间的相互作用关系添加边。
在此基础上构建邻域复形。由于蓝点的所有邻接点位于绿点集合中,反之亦然,因此最终得到了两个单纯复形,分别由蓝点和绿点组成,借助 Dowker 复形探讨实体之间的相互作用关系。
C. H. Dowker, “Homology groups of relations,” Annals of mathematics, pp. 84– 95, 1952. L. Lovász, “Kneser’s conjecture, chromatic number, and homotopy,” Journal of Combinatorial Theory, Series A, vol. 25, no. 3, pp. 319–324, 1978.
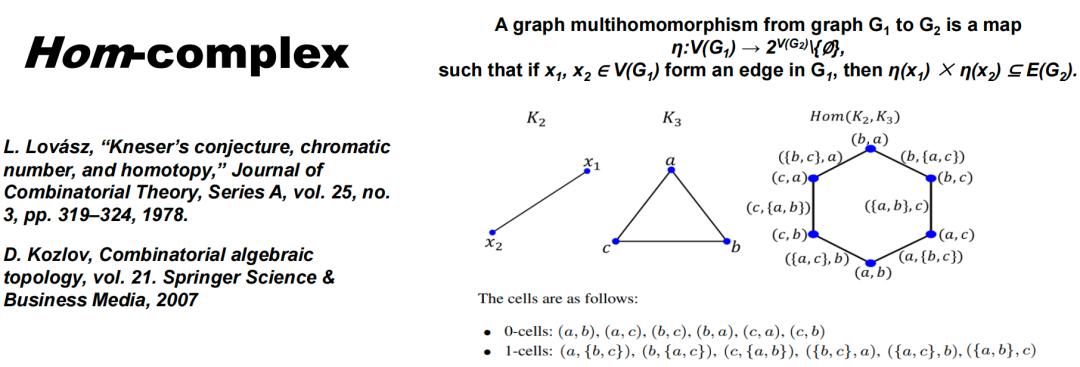
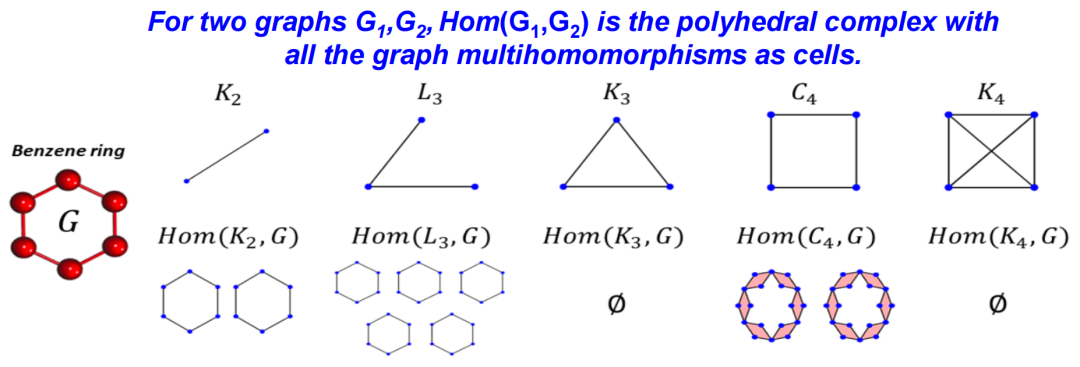
更复杂的场景可以用“Hom Complex”构造方式,这种方法适用于研究两个图的相互作用。其核心是构建一个称为Polyhedral Complex 的结构,其中元素为多重同态(Multihomomorphisms)。
举个例子,假设有两个图 K2 和 K3,选择某种映射策略将 K2 映射到 K3 。这个映射只需保证:原图存在的边,映射到新图中也存在对应边。比如将 K2 的点 K1 映射到 K2 中的点 a,点 x2 映射到点 b。但如果尝试将点 K1 和 x2 都映射到点a,那就会出现问题,因为在原图中点 x1 和 x2 之间存在边,但在新图中,点 a 无法形成自环。
如上图所示,将 x2, x2分别映到单点集的映射构成零单形 0-cell,将其中一点映到二点集的映射构成了一单形 1-cell,所有这些映射 η 构成了复形 Hom(K2, K3)。当考虑更复杂的连接关系时,比如使用高阶或卷积核样式的关系进行映射,这种方法能够帮助生成新的单纯复形,进一步反映图在这种特定内核下的深层联系。
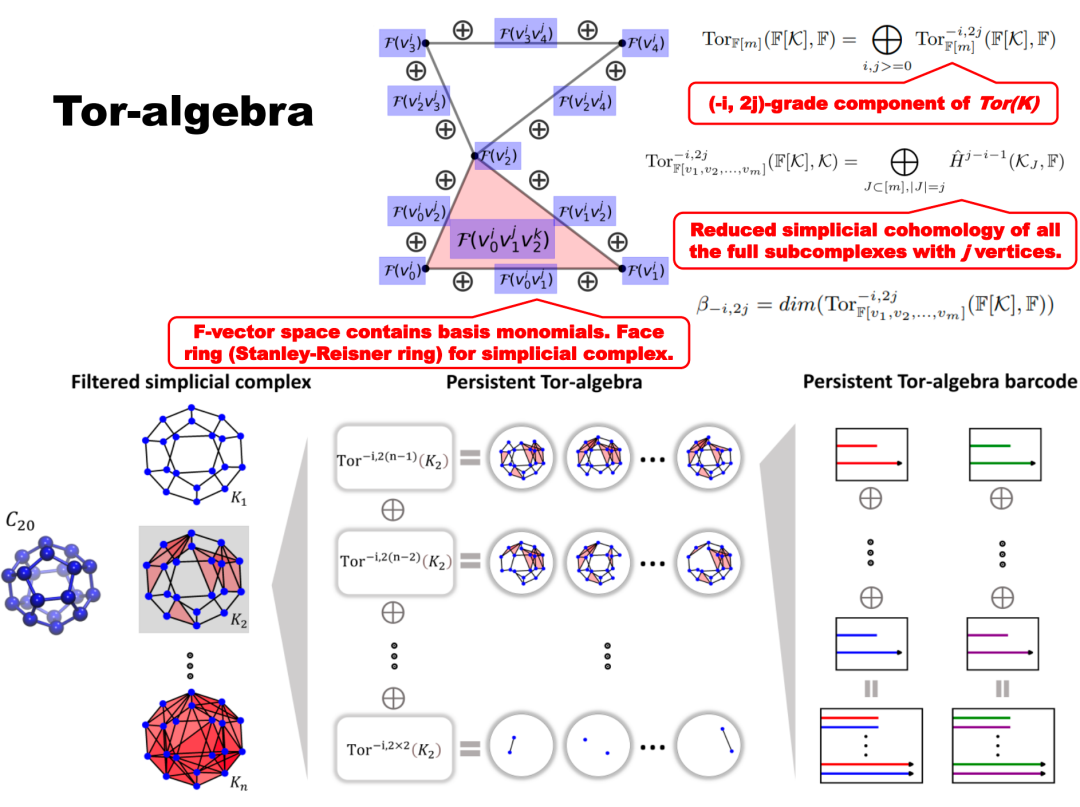
我们还能将单纯复形的结构提升到更复杂的代数结构进行考虑。比如,给定一个单纯复形,定义一组多项式,并在这些多项式之间建立特定的关系(例如Stanley-Reisner理论),进而得到一个理想(ideal)的结构,然后研究这个理想的性质,例如它的Tor函子等。这样,图的拓扑信息就被转换为了代数量,单纯复形上升到代数层面,在这个层面上进行研究。
Xiang, L. I. U., and Kelin Xia. “Persistent Tor-algebra based stacking ensemble learning (PTA-SEL) for protein-protein binding affinity prediction.” ICLR 2022 Workshop on Geometrical and Topological Representation Learning. 2022.
Persistent Tor-algebra(PTA)为生物学研究提供了一种强大且有效的新工具
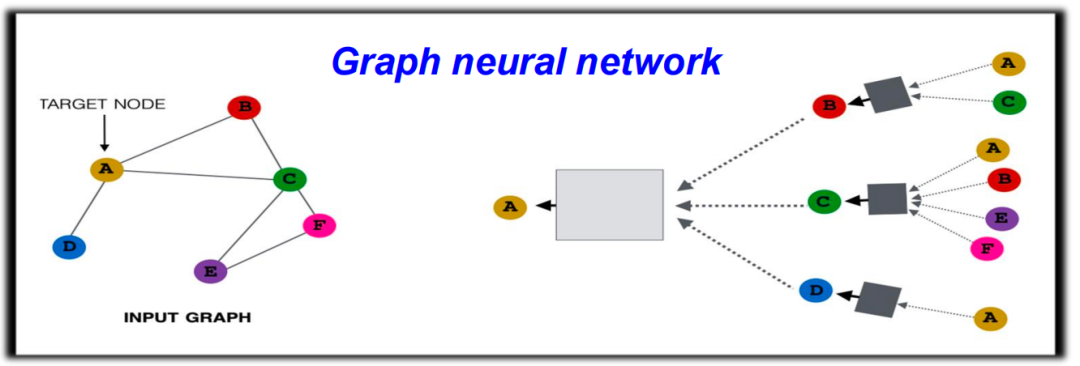
最后一部分,夏克林老师介绍了基于单纯复形的图神经网络,可以理解为图神经网络的一种扩展。在图神经网络中,核心的想法是通过消息传递(message passing)机制,将一个节点周围邻居的信息进行聚集,并传递到目标节点,然后通过迭代这个过程,实现对整个图结构的学习。
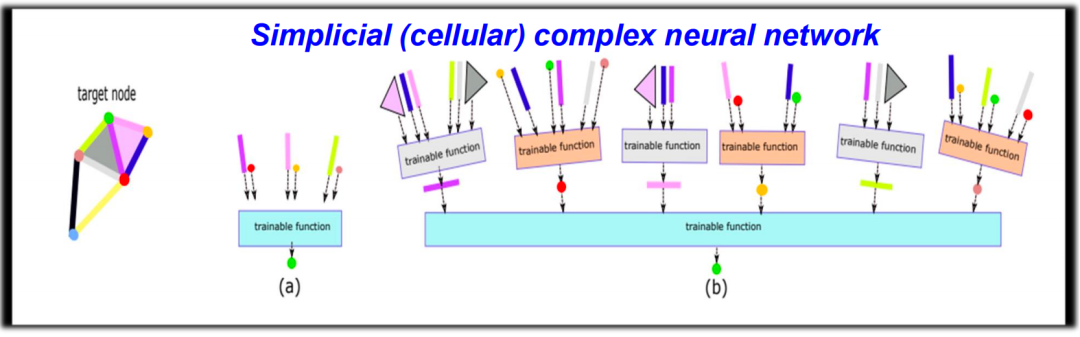
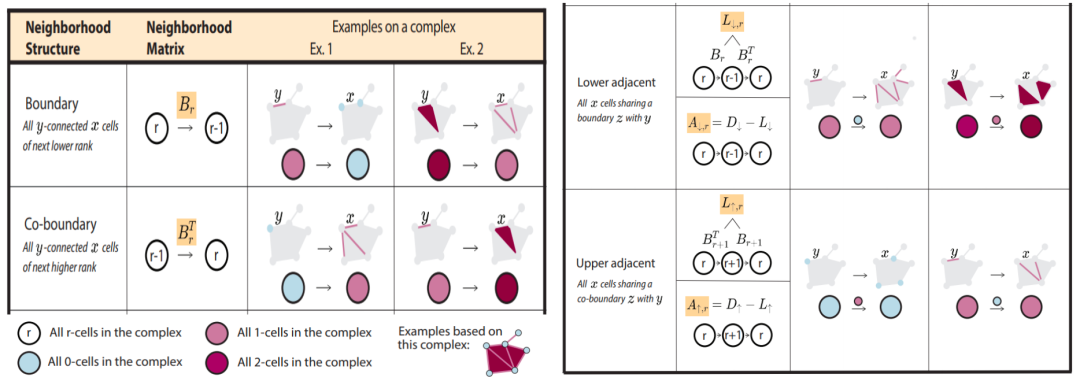
在拓扑数据处理中,我们不再只是基于图来操作,而是在更高维度的单纯复形或者其它复杂结构(例如Stellar complex)上进行操作。例如,除了在点的层面上进行信息传递,我们也可以在边、面或更高维度的单纯形上进行类似的操作。
在进行这种复杂的拓扑数据分析时,有两个非常核心的概念:边界运算(Boundary Operation)和余边界运算(Coboundary Operation)。简单来说,边界运算是指从给定的单纯形中找到其所有低一维的面。例如,从一个边(1-simplex)出发,我们可以找到它的两个端点(0-simplex)。而余边界运算则是反向操作,即从低维单纯形出发找高一维的单纯形。
除此之外,还有两个重要关系:Lower Adjacency 和 Upper Adjacency。这两个关系都是描述图中的邻接关系,但方式各异。Lower Adjacency指的是当两条边有一个公共顶点时,我们称这两条边是邻接的。而Upper Adjacency则更为严格,只有当两条边共享一个高维单纯形(比如三角形)时,我们才认为它们是邻接的。
通过考虑不同的连接方式,可以进一步描绘出数据中信息传递的不同路径,并通过将不同维度的信息耦合在一起,构建一个复杂的“拓扑神经网络”。
这种结合了拓扑和深度学习的研究领域还相对较新,但已经被广大学者所关注,并有越来越多的研究工作开始尝试利用拓扑数据分析来提升深度学习模型的性能。
Hajij, Mustafa, Kyle Istvan, and Ghada Zamzmi. “Cell complex neural networks.” arXiv preprint arXiv:2010.00743 (2020).
思考延伸
在拓扑数据分析(TDA)中,我们用单纯复形来表述和理解复杂的数据结构。然而,其他专业领域的研究者可能对这样的描述方式感到困惑。在他们眼中,原子(点)和共价键(边)具有明确的物理含义,而单纯复形中的三角形看起来似乎没有直观的物理意义?实际上,在 TDA 中,三角形捕获了三个元素之间的相互关系。在化学领域,这可以用来表示由三个原子组成的二个共价键之间的角度信息(bond angle)。而且这个角度信息在分子动力学的模拟中有极其重要的作用。然而,如何更好地定义单纯复形,并用它来描述体系中的高阶相互作用仍然是TDA建模中的一个主要问题。
另外一个 TDA 面临的挑战是如何将抽象的数学不变量与实际问题紧密联系起来。为了解决这个问题,我们需要理解这些拓扑特征所代表的实际意义。例如数据中的环状结构是否反映出它的物理、化学、生物,或其他实际信息。尽管 TDA 与传统图的方法在概念上有所不同,但其在刻画复杂的高阶相互作用的问题中展示出了极大的优越性,尤其是它可以刻画体系的最本质的拓扑信息。
在实际应用中,我们需要构造合适的单纯复形来描述高阶信息,并且找出拓扑不变量的合适的实际意义,这样才能发挥 TDA 模型真正作用,并使模型的解释性和性能得到提升。这就需要我们深入理解问题背景,将数学工具与实际问题紧密结合,并寻找到一个合适的应用场景来展示这种方法的优点。只有这样,TDA 才能表现其价值,并吸引更多人尝试使用这种新方法。
更进一步,除了拓扑数据分析,对于其他数学不变量,包括几何不变量、代数不变量、组合不变量等,也可以用于数据的表征和特征提取,这些模型将进一步促进我们对数据的本质信息的挖掘和刻画。为提高机器学习模型的精度、可解释性、迁移性等打下坚实的数学基础。
读书会地址:https://pattern.swarma.org/study_group_issue/540
夏克林,南洋理工大学副教授。2013年1月获得中国科学院博士学位,于2009年12月至2012年12月在美国密歇根州立大学数学系作为访问学者。从2013年1月至2016年5月,在密歇根州立大学担任访问助理教授。2016年6月,加入南洋理工大学,并于2023年3月晋升为副教授。夏克林的研究专注于分子科学的数学人工智能,在《SIAM Review》、《Science Advances》、《npj Computational Materials》、《ACS nano》等期刊上发表了70多篇论文。
数十年来,人工智能的理论发展和技术实践一直与科学探索相伴而生,尤其在以大模型为代表的人工智能技术应用集中爆发的当下,人工智能正在加速物理、化学、生物等基础科学的革新,而这些学科也在反过来启发人工智能技术创新。在此过程中,数学作为兼具理论属性与工具属性的重要基础学科,与人工智能关系甚密,相辅相成。一方面,人工智能在解决数学领域的诸多工程问题、理论问题乃至圣杯难题上屡创记录。另一方面,数学持续为人工智能构筑理论基石并拓展其未来空间。这两个关键领域的交叉融合,正在揭开下个时代的科学之幕。
为了探索数学与人工智能深度融合的可能性,集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师,共同发起“人工智能与数学”读书会,希望从 AI for Math,Math for AI 两个方面深入探讨人工智能与数学的密切联系。本读书会是“AI+Science”主题读书会的第三季。读书会自9月15日开始,每周五晚20:00-22:00,预计持续时间8~10周。欢迎感兴趣的朋友报名参与!
详情请见:
人工智能与数学读书会启动:AI for Math,Math for AI