关键词:张量网络,量子计算,全息量子纠错码,反德西特/共形场论,重整化群流

论文题目:Holographic codes from hyperinvariant tensor networks
期刊来源:Nature Communications
斑图地址:https://pattern.swarma.org/paper/8b978406-80e6-11ee-8dba-0242ac17000e
论文地址:https://www.nature.com/articles/s41467-023-42743-z
量子纠错领域虽然与量子计算的实际应用密切相关,但也与高能理论和量子引力有着深刻的联系。这一点在反德西特/共形场论(AdS/CFT)对应中得到了体现,AdS/CFT 理论提出一种猜想的对偶性,将(d+1)维体量子引力与渐近 AdS 时空背景上的d维 CFT 联系起来。这种对偶性意味着这两个理论之间存在一个关于算子和场的词典,而这个词典的细节展示了量子纠错码的定义特征。
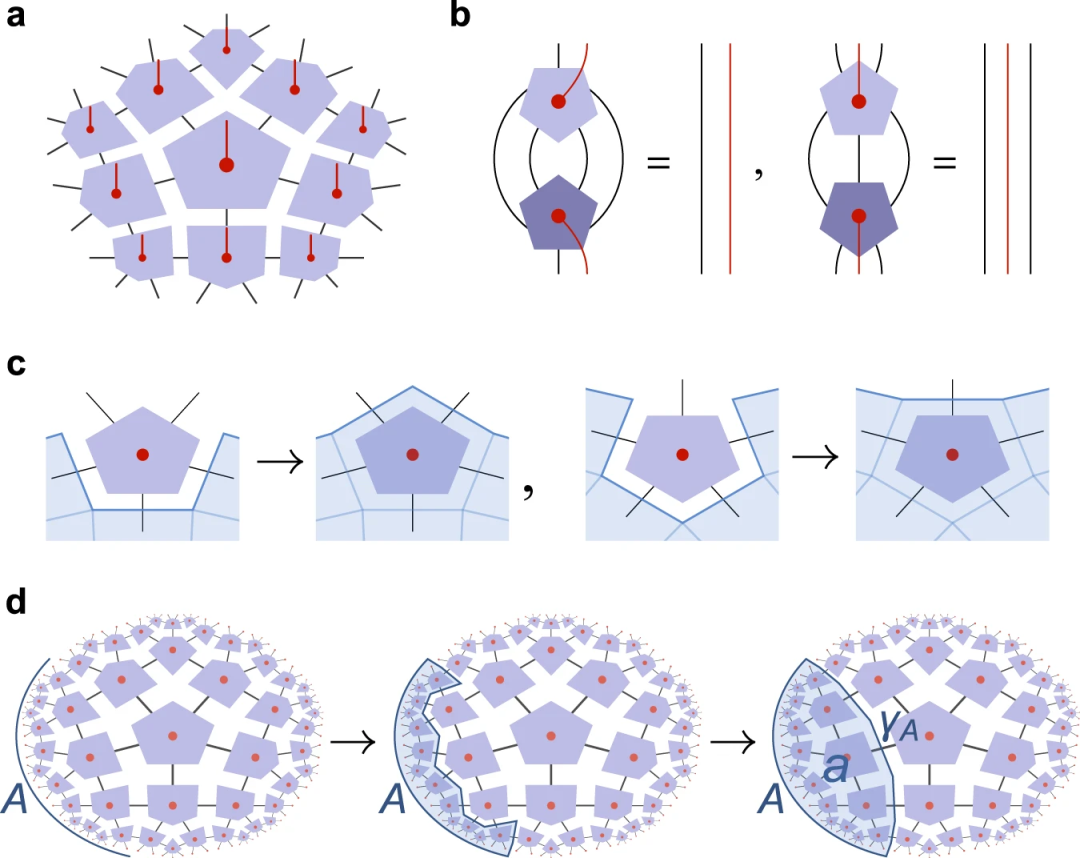
全息量子纠错码是关于体/边界对偶性的模型,例如反德西特/共形场论(AdS/CFT)对应,其中高维体几何与编码的逻辑自由度相关联。先前基于张量网络的离散全息编码复制了从连续 AdS/CFT 中可预期的一般编码属性,例如互补恢复(complementary recovery)。然而,这类张量网络的边界状态通常不表现出CFT边界状态的预期关联函数。
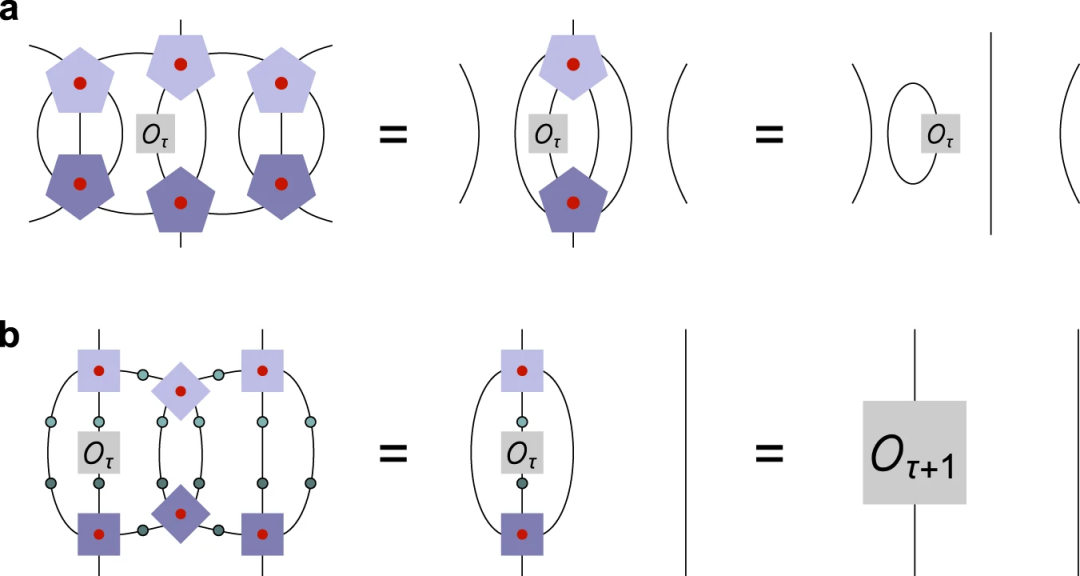
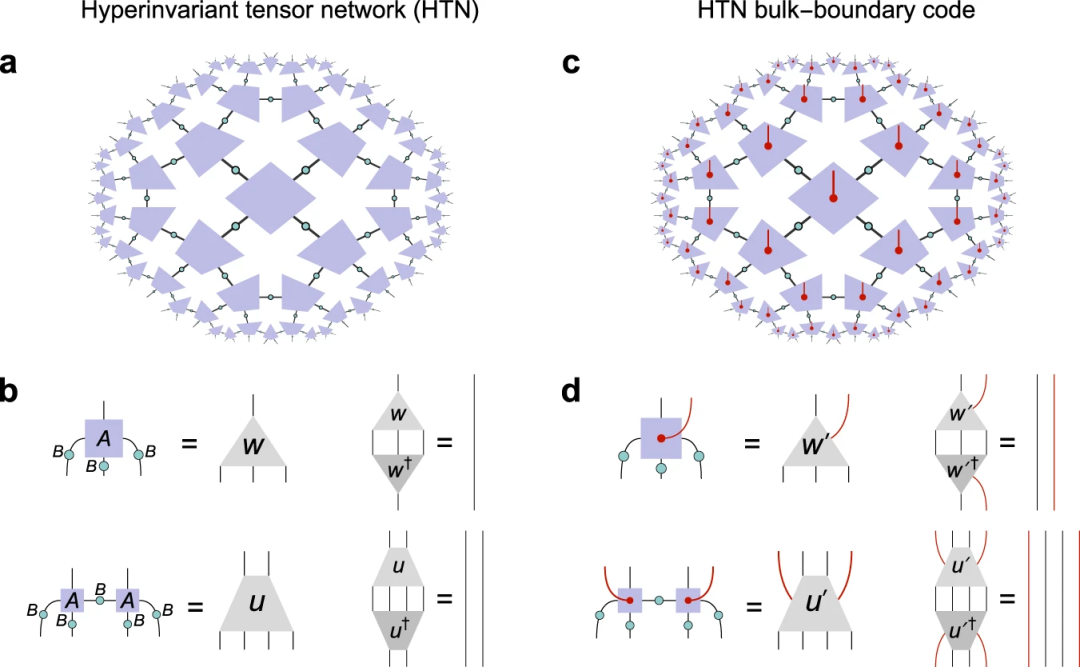
这项工作展示了一类新的精确全息码,将先前提出的超不变张量网络扩展到量子码,产生正确的边界关联函数。这种方法为体中的逻辑状态与边界状态的临界重整化群流之间建立了一个词典。此外,这些编码表现出与 AdS/CFT 在小的量子引力修正下预期的互补恢复的状态相关的破裂。
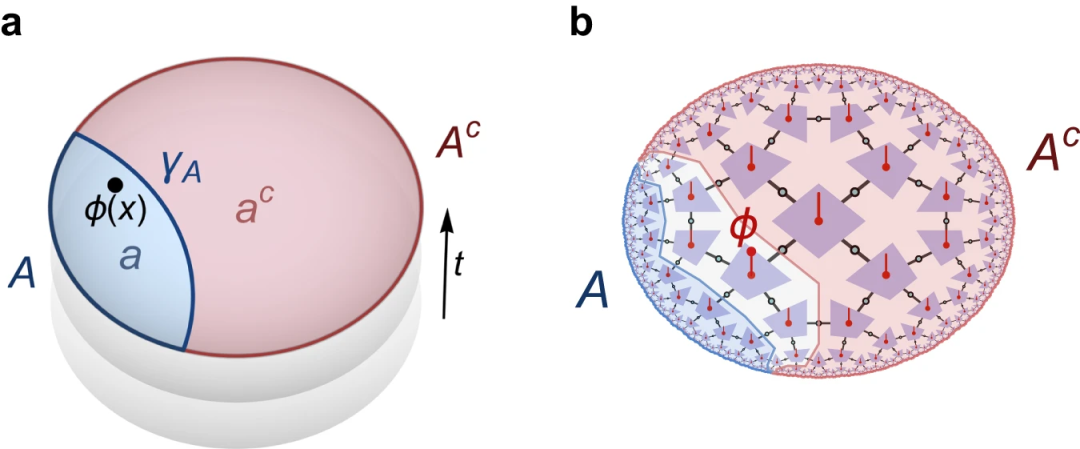
图1. 全息中的互补恢复。在连续的 AdS/CFT 理论中,对于固定时间t的切片,将边界CFT分成两个区域 A和 Ac 的二分法,等价于将体积分成两个纠缠楔形 a和 ac。在这里引入的全息张量网络编码中,边界的二分导致了被大量剩余区域(白色)分隔的体楔形;在这个区域内的算符 ϕ 通常无法同时在A和Ac上重构。
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅: