前沿进展:在组合优化问题中重新审视采样

导语

目录
-
采样算法概述
-
高效的离散空间采样算法
-
采样算法与组合优化
-
采样算法与AI模型
1. 采样算法概述
1. 采样算法概述
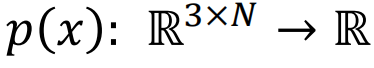 。如果对它运用Langevin Monte Carlo算法进行采样,就可以从部分数据迭代地生成一架完整的飞机。在采样过程中,很重要的一项是
。如果对它运用Langevin Monte Carlo算法进行采样,就可以从部分数据迭代地生成一架完整的飞机。在采样过程中,很重要的一项是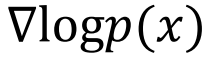 ,也叫做打分函数,在扩散模型的反向过程中也有类似的应用。但是我们知道,在离散空间中并不存在这样的梯度,因此一个关键问题就是解释
,也叫做打分函数,在扩散模型的反向过程中也有类似的应用。但是我们知道,在离散空间中并不存在这样的梯度,因此一个关键问题就是解释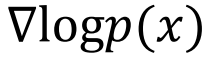 在离散空间中究竟对应着什么。
在离散空间中究竟对应着什么。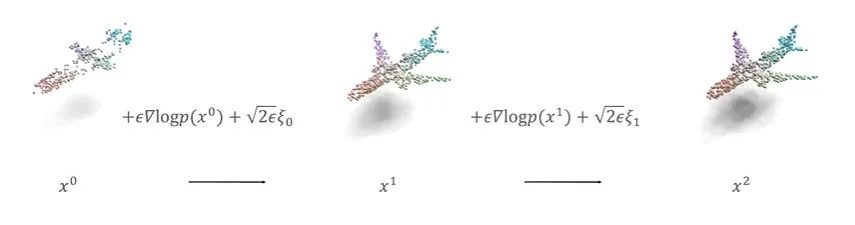
2. 高效的离散空间采样算法
2. 高效的离散空间采样算法
Sampling as first-order optimization over a space of probability measures [2022]. Anna Korba, Adil Salim. The variational formulation of the Fokker-Planck equation [1998]. Richard Jordan et al.

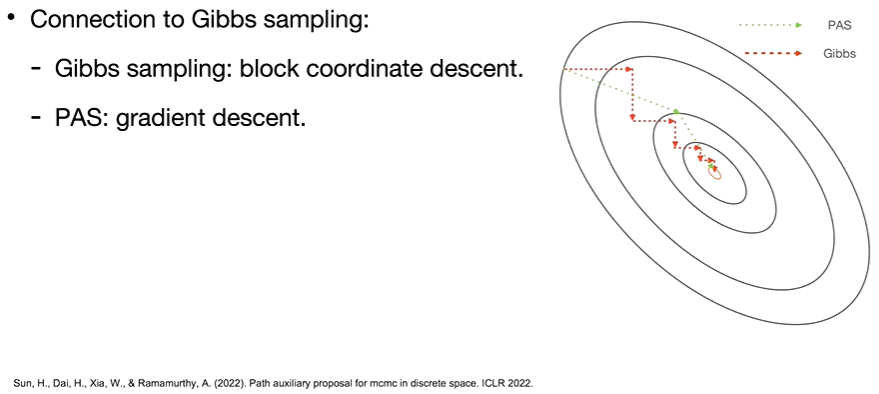
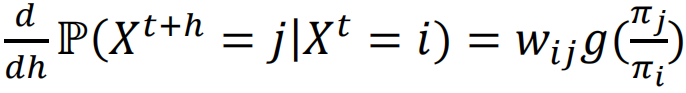 。进而,可以通过标准化模拟时间,计算转移概率矩阵,使用离散马尔科夫链的方法进行采样;也可以标准化每一步的汉明距离,使用称为Path Auxiliary Proposal的方法进行采样。图3展示了所提出的梯度下降采样算法与Gibbs这种算法相比的优势。
。进而,可以通过标准化模拟时间,计算转移概率矩阵,使用离散马尔科夫链的方法进行采样;也可以标准化每一步的汉明距离,使用称为Path Auxiliary Proposal的方法进行采样。图3展示了所提出的梯度下降采样算法与Gibbs这种算法相比的优势。Fokker-Planck equations for a free energy functional or Markov process on a graph [2012]. Shui-Nee Chow et al.
Discrete Langevin sampler via Wasserstein gradient Flow [2023]. Haoran Sun et al. Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium [2005]. Hong Qian, Daniel A Beard. Path auxiliary proposal for MCMC in discrete space [2022]. Haoran Sun et al.
3. 采样算法与组合优化
3. 采样算法与组合优化
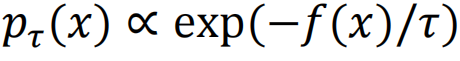 ,则可以对概率空间
,则可以对概率空间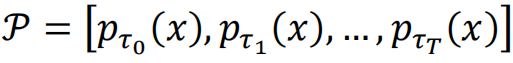 (τ0>τ1…τT→0)作采样,来求解组合优化问题。前面提到的Path Auxiliary采样也可以用于组合优化问题,每步改变一个状态,从而在目标状态改变多个结点。
(τ0>τ1…τT→0)作采样,来求解组合优化问题。前面提到的Path Auxiliary采样也可以用于组合优化问题,每步改变一个状态,从而在目标状态改变多个结点。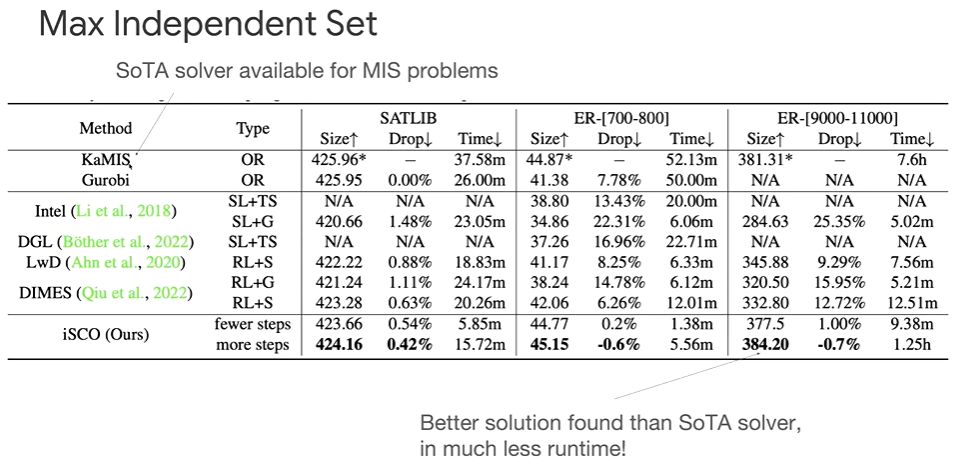
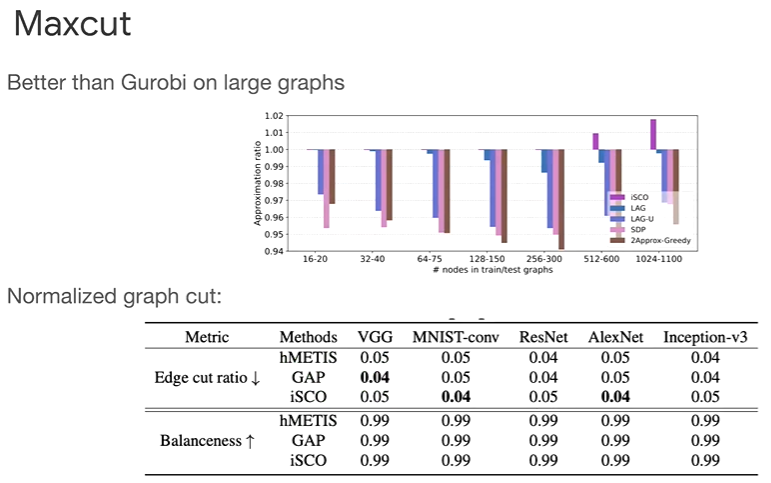
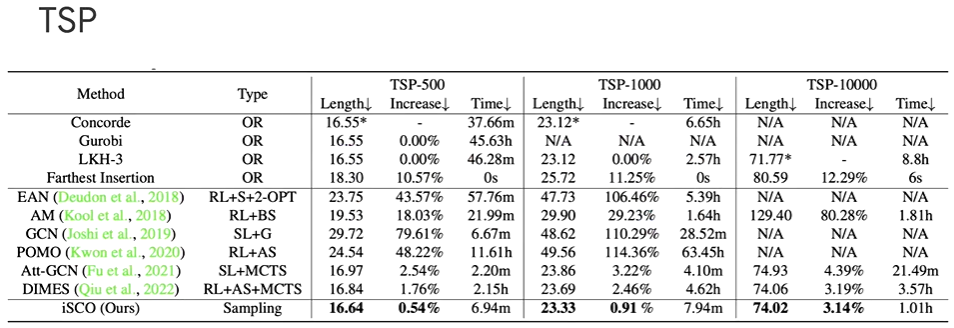

Revisiting Sampling for Combinatorial Optimization [2023]. Haoran Sun et al.
4. 采样算法与AI模型
4. 采样算法与AI模型



学者简介

戴涵俊,Google DeepMind实验室资深科学家和研究经理,此前于佐治亚理工获得博士学位。研究方向:高效的生成模型,包括大语言模型,图像和结构化数据模型,及其采样和优化的底层算法
图神经网络与组合优化读书会

推荐阅读










