在复杂多变的协作系统(例如联合申报项目或组队完成任务)中,如何有效地促进个体间的合作是一个值得深入探讨的挑战性问题。《IEEE Transactions on Network Science and Engineering》最新发表的研究论文“Limitation of Time Promotes Cooperation in Structured Collaboration Systems”为我们提供了新的洞见。该研究通过构建一个时序博弈框架,深入分析了有限协作时间对个体合作行为的影响,并在大规模实证实验中验证了理论模型预测的准确性。研究发现,当协作时间对每个个体都同样是有限时,系统整体的合作水平将得到显著提升。
张毅超 | 作者
Limitation of time promotes cooperation in structured collaboration systems
https://ieeexplore.ieee.org/document/10720394
同济大学的张毅超教授及其团队在最新研究[1]中发现,当个体的互动和决策时间受到限制时,群体的合作水平会得到提升。这一理论发现不仅在模拟实验中得到验证,还在超过1400名志愿者参与的系统性实验中得到证实,为真实协作网络中高合作水平的存在提供了理论支持。
该研究首先构建了一个时序博弈框架,将理性个体间的互动嵌入到含时二人博弈(two-players game)中。基于这一框架,研究者能够研究含时互动的复杂性和可变性,以及这些因素如何影响社会行为。研究发现,在时间受限的情况下,个体更倾向于合作,这一趋势在基于Barabasi and Albert (BA) 无标度和Watts and Strogatz (WS) 小世界网络模型的模拟中得到了验证。
为了在人类协作系统中验证这一理论推断,研究进一步通过在线博弈平台“War of Strategies”进行验证。实验分为预设结构和自组织两种模式。在预设结构模式下,被试者会被放置在预先生成的网络结构中进行囚徒困境博弈;在自组织模式下,被测试者有一分钟时间来完成交友活动;比赛开始后,协作网络结构将被冻结。在每种模式下,平台分别开设了含时与不含时两种博弈场景。在含时场景中,每位被试者的协作时间相同且有限;在不含时场景中,每位被试者在一轮中可以跟任意多好友博弈,只要对方接受博弈请求。
结果显示,在含时场景下,参与者的合作比例显著高于无时间限制的不含时场景。
该研究的重要性在于,它不仅揭示了人类合作的一个重要激励因素,还为设计更有效的合作机制提供了理论支持。在现实世界中,无论是项目管理、团队合作还是社交活动,时间限制都是一个不可忽视的因素。理解时间限制如何影响合作行为,可以帮助我们设计更好的协作策略,提高协作效率。
该研究提出的时序博弈模型基于[1,2]中提出的分治博弈框架,并在设计之时考虑了时间资源,给博弈者之间的交互行为(合作或背叛)分配一定的持续时间。在一轮博弈中,个体的总协作时间被设定为一个常数,与现实协作场景保持一致。假设玩家与不同玩家的交互作用是独立的。玩家i和j之间的博弈收益被形式化定义为:
其中,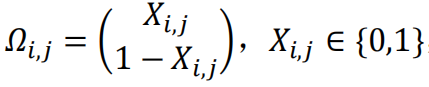 ,取值为1表示玩家i选择与玩家j合作(C),0表示玩家i选择背叛玩家j(D);R表示互相合作的奖励(C-C),T表示背叛合作者的奖励(D-C),S表示与背叛者合作的收益(C-D),P表示互相背叛的收益(D-D)。
其中,Ni表示个体i的邻居集合,τi,j表示个体i与个体j交互(C/D)的时间,满足
,取值为1表示玩家i选择与玩家j合作(C),0表示玩家i选择背叛玩家j(D);R表示互相合作的奖励(C-C),T表示背叛合作者的奖励(D-C),S表示与背叛者合作的收益(C-D),P表示互相背叛的收益(D-D)。
其中,Ni表示个体i的邻居集合,τi,j表示个体i与个体j交互(C/D)的时间,满足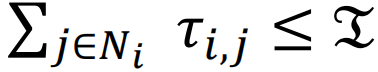 ,此外用𝔗表示个体每一轮博弈拥有的总时间资源,为一个设定的常数。
,此外用𝔗表示个体每一轮博弈拥有的总时间资源,为一个设定的常数。
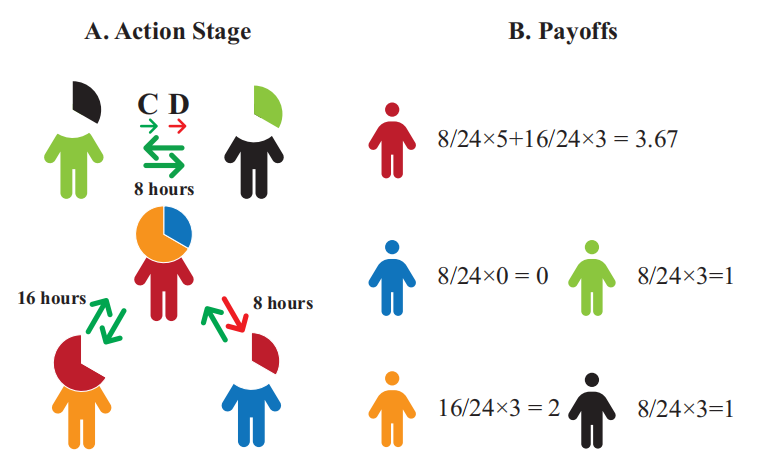
图1:时序博弈框架示意图。子图A显示的是一轮五个人之间的博弈。其中,𝔗 = 24,𝑅 = 3, 𝑆 = 0, 𝑇 = 5, 𝑃 = 1。
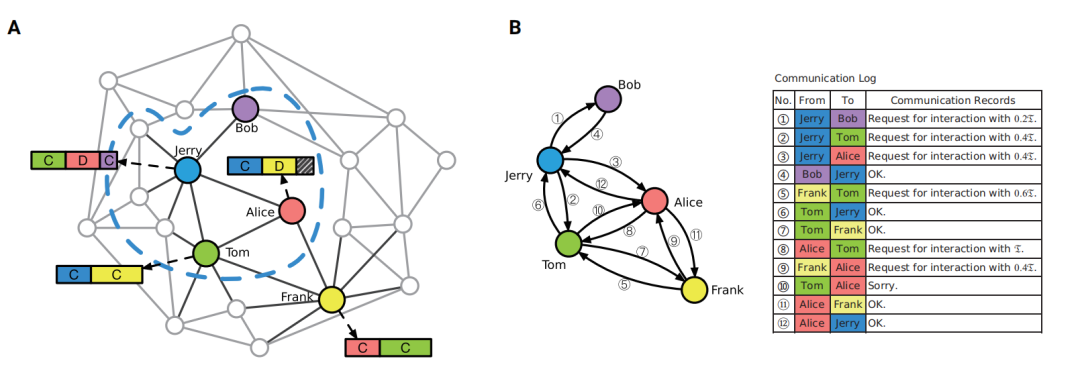
图1和图2分别从不同尺度和视角展示了上述时序博弈系统。图1形象化地展示了每轮个体整体收益的计算方法,图2则以协作系统中的几个个体组成的子系统为例,展示了一轮博弈中个体之间交互的全过程。如图所示,Alice有三位邻居,分别是Tom、Jerry和Frank。首先,Alice试图与Tom协作𝔗时间,而Tom在收到Alice的请求时已经同意与Jerry和Frank协作。因此,Alice转向Frank和Jerry,但此时Frank和Jerry无法提供Alice所需的协作时间。因此,Alice分别拿出0.4𝔗与Frank和Jerry协作。这使得其在这一轮浪费了0.2𝔗。本例展示了该框架的核心思想,请求的成功与否主要取决于被请求用户是否有时间接纳该协作请求。由于每个人的协作时间是有限的,有些请求是无法被接纳的。因此,个体之间的协作除了主观意愿之外,还要收到有限协作时间的约束,这进一步增加了人类建立新协作关系的难度。
研究团队设计了一系列在线博弈竞赛,以模拟现实世界中的二人博弈系统。比赛分为两个阶段:第一阶段,参与者在网络平台上被动或主动组织成一张协作网络;第二阶段,进行多轮的囚徒困境博弈。在被动组织成的协作网络中,参与者被随机分配到预设网络节点上;而在自组织模式中,他们是通过聊天室功能自行寻找博弈伙伴的。无论在哪种模式下,他们协作与否以及协作时间的长短都由自己决定,模拟了现实社会中的真实协作模式。每轮博弈中,个体可以向其朋友发送协作请求,请求中包含协作持续的时间。这些请求可以被接受、拒绝、忽略或取消。是否接受请求由被试者自身需求或发送请求者的博弈历史来决定。当然,接受请求的前提是保证接受后,总协作时间不超过个体协作时间的上限。博弈的收益与双方商定的协作时间长短成正比,体现了时间资源在协作中的重要性。
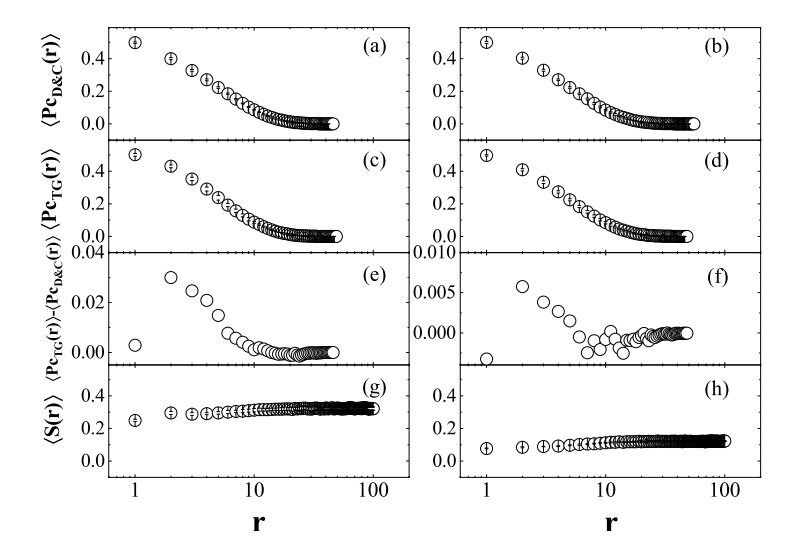
图3:分治博弈与时序博弈下协作网络的合作水平演化(模拟实验)
在分治博弈中,每个参与者会将协作时间平均分配给所有的邻居,而在时序博弈中,参与者可以根据具体情况自由分配时间。在时序博弈中,由于时间资源有限,最终的分配受双方沟通过程的影响。只有当双方个体的可用时间均大于协作所需时间时,协作请求才能被接纳。另一方面,分治博弈不受有限时间的影响,只要个体同意,所收到的全部博弈请求都可以被接纳。为了消除社交关系数量差异所引入的不公平性,比赛以每对协作者的平均收益来决定参与者的收益排名。
如图3(a)和图3(b)所示,在BA和WS网络中,模拟实验中的智能体在进行“分而治之”(D&C)博弈时,合作水平会随着回合数的增加而衰减。如图3(c)和3(d)所示,在受到时序博弈中有限协作时间的影响后,合作水平衰减速率明显减慢。分而治之博弈与时序博弈之间的合作水平差异如图3(e)和3(f)所示。在模拟实验中这种差异看起来很小,但当人类被试者进行博弈时,这种差异会被显著放大。这种放大可能是由图3(g)和图3(h)所示的系统可用时间资源S(r)短缺引起的。当人类进行时序博弈时,S(r)会比模拟时低得多。这是由于人类可以调整博弈请求以适应好友的时间表,而在模拟中智能体的时间再分配策略并没有整合这一机制。
图4:时序博弈的合作水平与平均可用时间演化图(人类实验)
通过对比图4(a)和图4(b),我们可以看到,在时序博弈中合作水平的衰减比分而治之博弈中的要慢。结果证实了理论预测,表明时间限制促进了现实协作网络中的合作水平。
BA网络和WS网络的平均可用时间S(r)演化分别如图4(c)和图4(d)所示。可以看到S(r)围绕一个小值波动,这表明当人类进行时序博弈时寻找新伙伴的难度比模拟实验中智能体更大。模拟实验与人类实验中整体合作水平Pc(r)的差异表明,寻找新合作伙伴难度的上升可能导致Pc(r)的提升,这在一定程度上解释了时序博弈中的有限时间设定为何能提升人类协作网络中的合作水平。
这项研究为理解人类合作行为提供了新的视角,特别是在协作时间受限环境下的群体合作行为。它不仅丰富了我们对演化博弈的理解,也为如何在现实协作系统中促进合作提供了可行的路径。随着研究的深入,我们希望在未来能看到更多关于时间与人类合作行为之间相关性的研究,为人类在非合作博弈中的合作行为提供更多的科学依据。
[1] Y. Zhang, G. Chen, J. Guan, Z. Zhang, S. Zhou, “Unfavorable individuals in social gaming networks,” Scientific Reports, vol. 5, p. 17481, 2015.
[2] J. Wang, Y. Zhang, J. Guan, S. Zhou, “Divide-and-conquer tournament on social networks,” Scientific Reports, vol. 7, p. 15484, 2017.
网络科学系列课1:巴拉巴西网络科学,全面系统讲解网络科学,从图论、随机网络、无标度网络、BA模型、演化网络、度相关性、网络鲁棒性、社区发现、网络传播等,帮助大家完成从散点思维到网络思维,直至网络科学思维的跃升。详情及试看:
https://campus.swarma.org/course/1754
网络科学系列课2:网络科学导论,系统地介绍网络科学的基本概念、思想和方法,网络动力学是其核心部分,通过网络拓扑和动力学相结合的研究,可以实现对复杂系统的预测和控制。详情及试看:
https://campus.swarma.org/course/2328
https://campus.swarma.org/course/3533
高阶网络读书会,结合单纯复形(simplex)表示模型展开。重点讨论研究发展出的基于超图、单纯复形、依赖关系等的网络高阶表示模型,能够用于研究在许多真实的复杂系统中,广泛存在多个体同时(或以特定顺序)进行交互的高阶交互现象。详情及试看:
https://pattern.swarma.org/study_group/17
![]()
推荐阅读
6. 加入集智,一起复杂!
点击“阅读原文”,报名课程


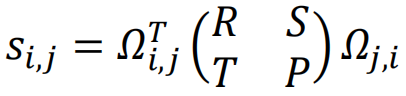
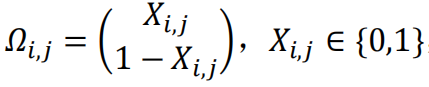 ,取值为1表示玩家i选择与玩家j合作(C),0表示玩家i选择背叛玩家j(D);R表示互相合作的奖励(C-C),T表示背叛合作者的奖励(D-C),S表示与背叛者合作的收益(C-D),P表示互相背叛的收益(D-D)。
,取值为1表示玩家i选择与玩家j合作(C),0表示玩家i选择背叛玩家j(D);R表示互相合作的奖励(C-C),T表示背叛合作者的奖励(D-C),S表示与背叛者合作的收益(C-D),P表示互相背叛的收益(D-D)。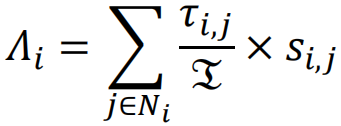
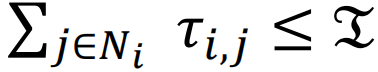 ,此外用𝔗表示个体每一轮博弈拥有的总时间资源,为一个设定的常数。
,此外用𝔗表示个体每一轮博弈拥有的总时间资源,为一个设定的常数。