Nat. Commun.前沿:从实验数据中学习可解释的随机复杂系统动力学

赵沐阳 | 编译

论文题目:Learning Interpretable Dynamics of Stochastic Complex Systems from Experimental Data 论文地址:https://www.nature.com/articles/s41467-024-50378-x
1. LaGNA 框架
1. LaGNA 框架
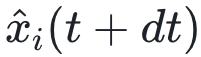 与xi(t+dt)的差值会造成过拟合的情况。所以本文考虑
与xi(t+dt)的差值会造成过拟合的情况。所以本文考虑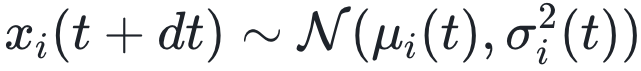 , 其中
, 其中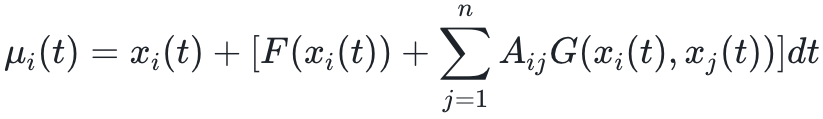 以及
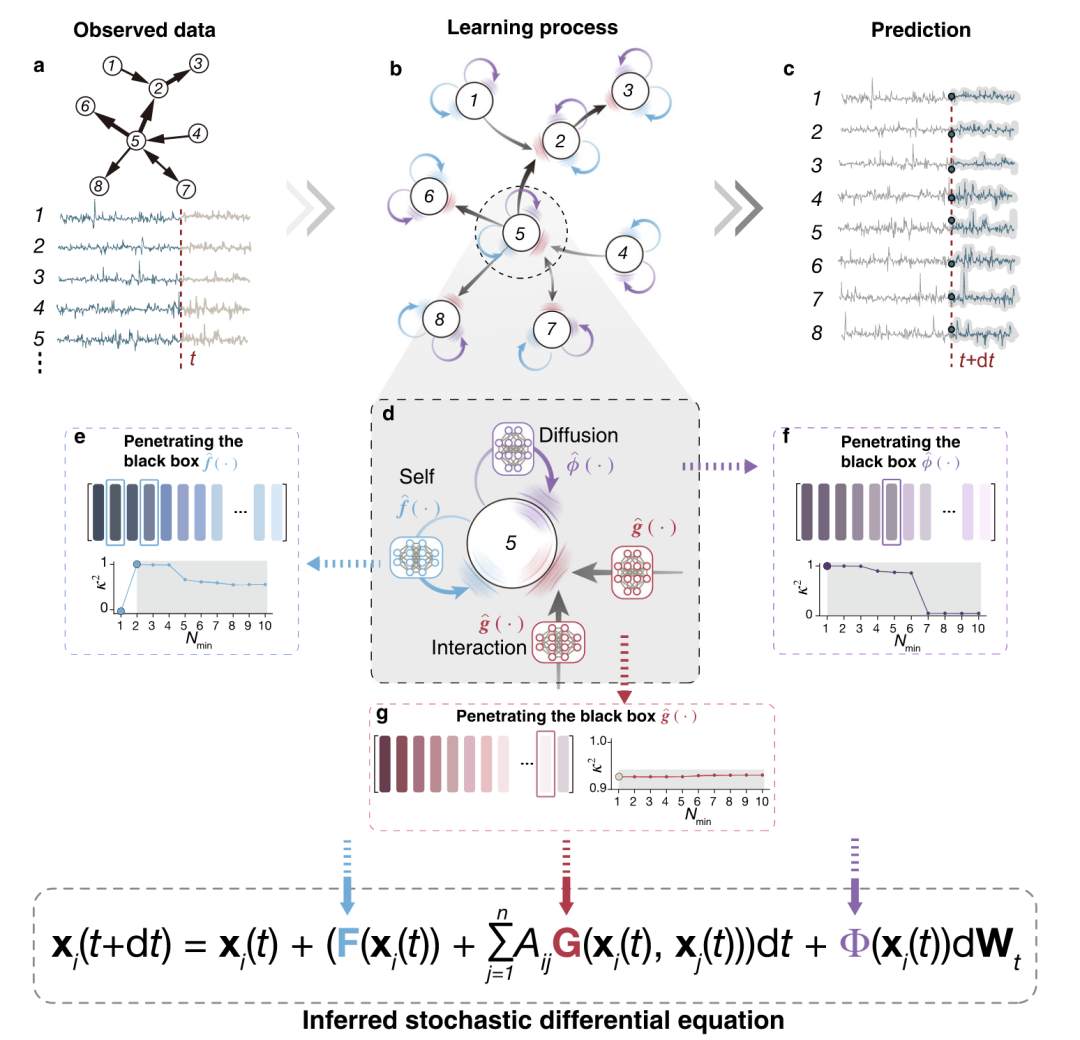
以及 为了对网络进行端到端训练,使用所有节点在时刻t的状态 xt 作为输入。基于网络拓扑Aij,使用函数 g(xi(t), xj(t)) 映射节点j到节点i的信息流。估计的信息值随后按元素进行聚合,汇总接收节点在所有相应发送节点上的值。此外,使用函数f(xi(t))映射每个节点i的自动态。节点i的活动分布的估计均值和方差可以分别写为
为了对网络进行端到端训练,使用所有节点在时刻t的状态 xt 作为输入。基于网络拓扑Aij,使用函数 g(xi(t), xj(t)) 映射节点j到节点i的信息流。估计的信息值随后按元素进行聚合,汇总接收节点在所有相应发送节点上的值。此外,使用函数f(xi(t))映射每个节点i的自动态。节点i的活动分布的估计均值和方差可以分别写为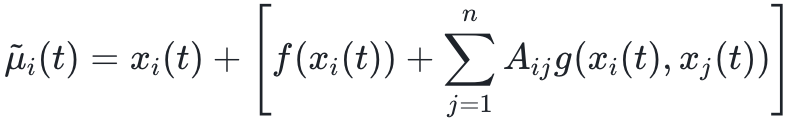 和
和 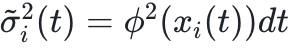 函数g,f和Φ分别由可训练的参数
函数g,f和Φ分别由可训练的参数 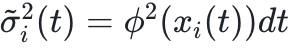 、θg和θΦ决定。
、θg和θΦ决定。
2. 自动力学、交互动力学、扩散过程的推理
2. 自动力学、交互动力学、扩散过程的推理
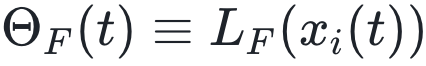 、
、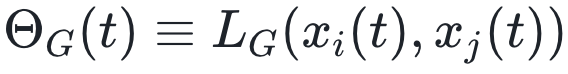 和
和 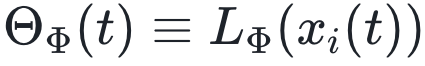 。然后,推理问题可以用如下估计值表示:
。然后,推理问题可以用如下估计值表示: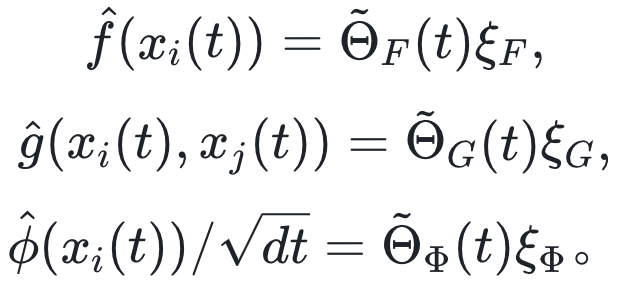
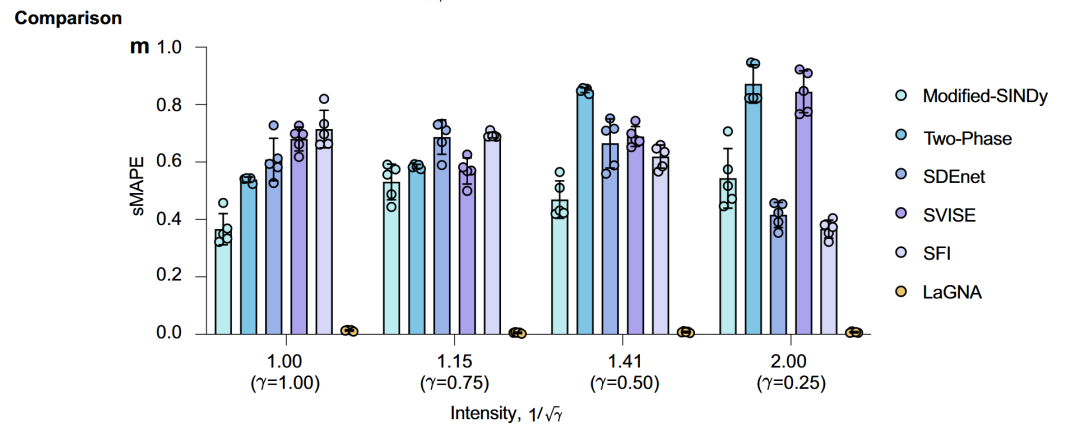
图2. 以随机洛伦兹网络动力系统作为基准,与现有的五种主流的符号学习方法进行对比,可以发现LaGNA最准确。
3. 真实场景数据
3. 真实场景数据
3.1 从真实数据中推理鸟群的动力系统

图3. a:20只鸟在二阶Vicsek模型下生成的3维轨迹。b–e:显示第一维度的扩散、自动态、凝聚和对齐强度,分别由函数Φ(·)、f(·)、ga(·)和 gc(·)估计,并与Vicsek模型真实值进行对比。f:通过推断出的随机Vicsek动力学生成的鸟群轨迹。g–p:从四个实测数据集推断鸟群聚集动力学。g 对比了推断的SDE生成的力场与从实测数据中计算出的力场。h 为使用推断出的SDE生成的8只鸽子在不同时间点t=25,50,100的轨迹,子图显示了实测数据中的第一维轨迹。i–j 为推断SDE的对齐和凝聚强度函数的可视化结果。k–p 分别显示推断SDE生成的第二、三和四个鸟群数据的轨迹和力场对比。
3.2 推理 tau 病理学在小鼠大脑中的传播动力学
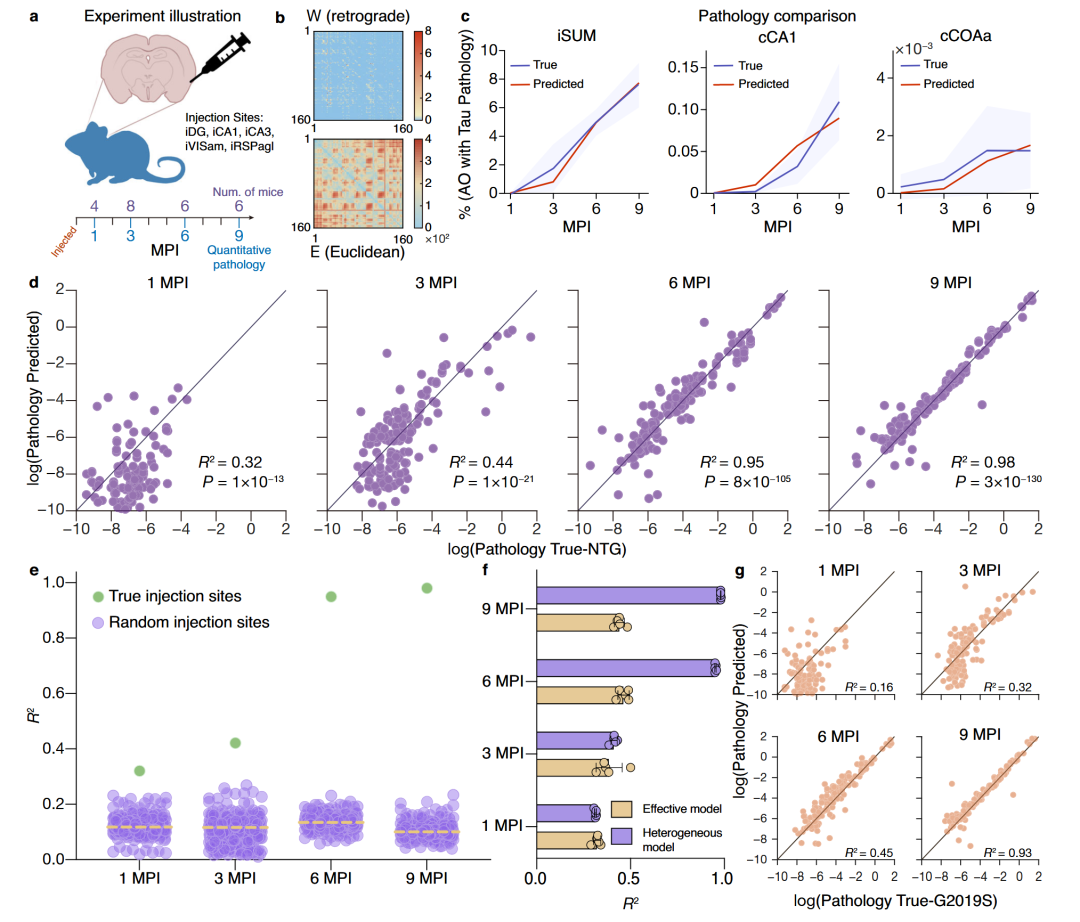
图4. a:实验数据: 非转基因(NTG)小鼠在3-4个月大时被单侧注射了阿尔茨海默病(AD)PHF tau,注射部位包括iDG、iCA1、iCA3、iVSt/iam和iRSPagl。小鼠在注射后1、3、6和9个月(MPI)被安乐死,并记录病理扩散情况。b:神经解剖学连接图,包括逆行(上)和欧几里得近端连接(下)。c:实际和预测的tau病理占据面积(AO)随时间的对比,显示了在iSUM、cCA1和cCOAa部位的tau病理扩散情况,阴影区域表示标准差。d:不同时期(1、3、6和9 MPI)的log尺度下tau病理预测与真实值的对比,展示了皮尔逊相关系数R2和P值。e:随机选择5个注射部位(500次独立运行)的预测扩散模式(紫色点)与从真实注射部位开始的预测结果(绿色点)的对比。f:隐式有效模型和显式异质模型之间的预测对比,误差条表示标准差。g:LRRK2G2019S 突变小鼠病理数据中推断扩散方程的有效性。
4. 总结
4. 总结
参考文献
复杂系统自动建模读书会第二季
“复杂世界,简单规则”。
集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云,共同发起「复杂系统自动建模」读书会第二季。
读书会将于9月5日起每周四晚上20:00-22:00进行,探讨四个核心模块:数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断(动力学+网络结构)、应用-超材料设计和城市系统,通过重点讨论75篇经典、前沿的重要文献,从黑盒(数据驱动)到白盒(可解释性),逐步捕捉系统的“本质”规律,帮助大家更好的认识、理解、预测、控制、设计复杂系统,为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与!
复杂系统自动建模读书会:从数据驱动到可解释性,探索系统内在规律|内附75篇领域必读文献
6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会










