摘要


在热力学中，功率和效率是衡量热机性能的两个主要参数。根据经典热力学，可逆热机效率的上限是卡诺效率，但相应的功率为零。这是因为卡诺效率的实现依赖于时间无穷长的准静态假设。因此，如何根据实际需求，在保证热机功率前提下提高热机效率成为热力学一个重要的科学挑战问题。在20世纪上半叶应运而生的有限时间热力学，今天得到了蓬勃发展，为应对这个挑战提供了必要的科学支撑。


本文主要介绍有限时间热力学的发展及现状，特别是最近对于有限时间热机功率效率约束关系及其优化问题上的研究。针对有限时间热力学循环功率—效率约束与不可逆性的关系，文章还简介作者关于有限时间等温过程中不可逆熵产生的理论和实验研究工作。最后展望未来有限时间热力学及有限系统非平衡物理的可能发展与应用。


关键词：有限时间热力学，实际热机优化，功率效率约束关系，不可逆熵产生

马宇翰、董辉、孙昌璞 | 作者

中国物理学会期刊网，选自《物理》2021年第1期 | 来源



活动预告：本周四晚（12月19日），集智俱乐部「非平衡统计物理」读书会邀请到北京师范大学物理学系讲师马宇翰分享有限时间热力学领域的最新进展。欢迎感兴趣的朋友参与！





鱼，我所欲也；熊掌，亦我所欲也，二者不可得兼，舍鱼而取熊掌者也。

——《孟子·告子上》


I want fish, and I also want bear’s paws. If I cannot have both of them, I will let the fish go, and take the bear’s paws.

——“Mencius· Gao Zi-shang”






1. 引言




当感觉到双手发冷时，人们会不由自主地通过向手心哈气或者搓手的行为来取暖。这一生活中的常见情景其实蕴含了自然界能量传递的两种方式：热传递和做功。早在远古时代，人类的祖先就学会了通过燧石碰撞或者钻木的方式进行取火，开始将热现象引入生活和生产的某些环节，并利用热能。火的发现和使用直接促进了原始人向智人的进化，让人类文明进入了火的时代。进而蒸汽机的发明导致了人类社会的第一次工业革命。

其实，直到17、18世纪经典力学建立完善之后，人们才开始对涉及热现象的能量转换过程进行集中系统的研究，形成了热力学这一新的学科。在这一时期，玻意尔 (R. Boyle)、迈耶 (J. R. Mayer)、焦耳 (J. P. Joule)、卡诺 (N. L. S. Carnot)、开尔文 (Lord Kelvin, 原名 W. Thomson) 和克劳修斯 (R. J. E. Clausius) 等著名的科学家和工程师分别引入了温度、压强、热和功等基本热力学量，对各种涉及热现象的能量转换过程进行了系统丰富且准确定量的研究，并基于大量的实验事实总结出了经典热力学中的基本规律。其中，热力学第一定律描述能量守恒，第二定律描写由熵增表征的不可逆过程，这些构成了热力学研究的核心框架[1]。

热力学把一些传热做功的研究对象抽象为热机。如图1所示，热机是一种工作在两个热源之间，从高温热源中提取热能并将其部分用于对外做功的机械装置。詹姆斯·瓦特 (J. Watt) 改良的蒸汽机就是早期具有实用价值的热机，它的出现引起了18世纪中叶从英国发起的第一次工业革命。此后，人们基于热力学规律设计了多种多样的热机，例如卡诺热机、奥托热机、狄塞尔热机等，并不断对这些热机的性能进行优化。这些工作大大地提高了生产效率，加速了社会进步，并进一步引发了此后两个世纪科学与技术革命。

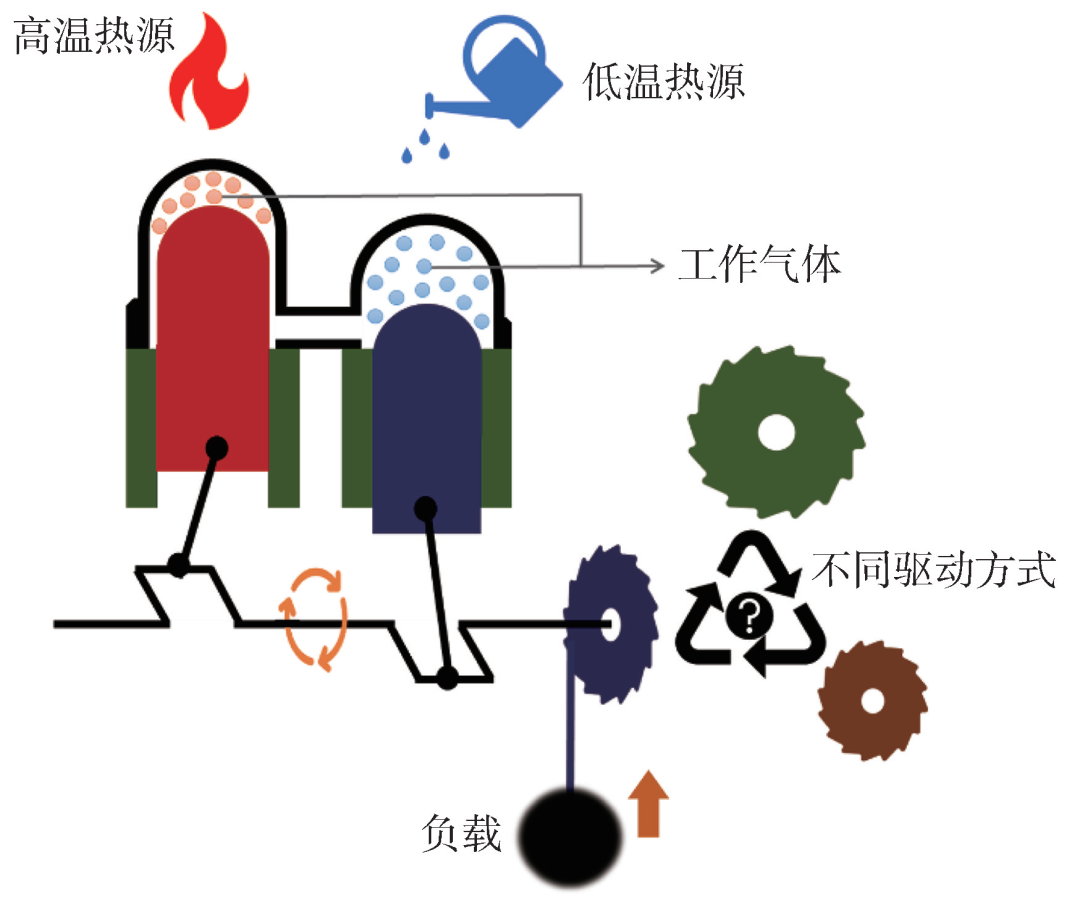
图1 热机示意图：在这一简单的热机模型中，气缸中的气体在两个热源间周期性地膨胀和压缩，使得气缸推动连杆带动轴转动，带动重物上升。热机从热源间吸收的能量部分转化为所提升重物的重力势能。热机的性能由做功物质和热源的热力学性质，以及驱动热机的方式决定


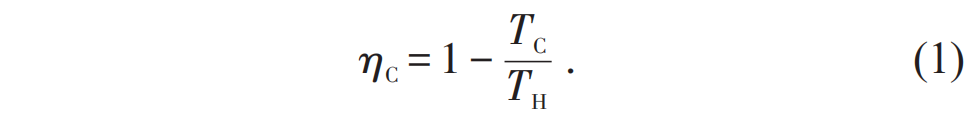
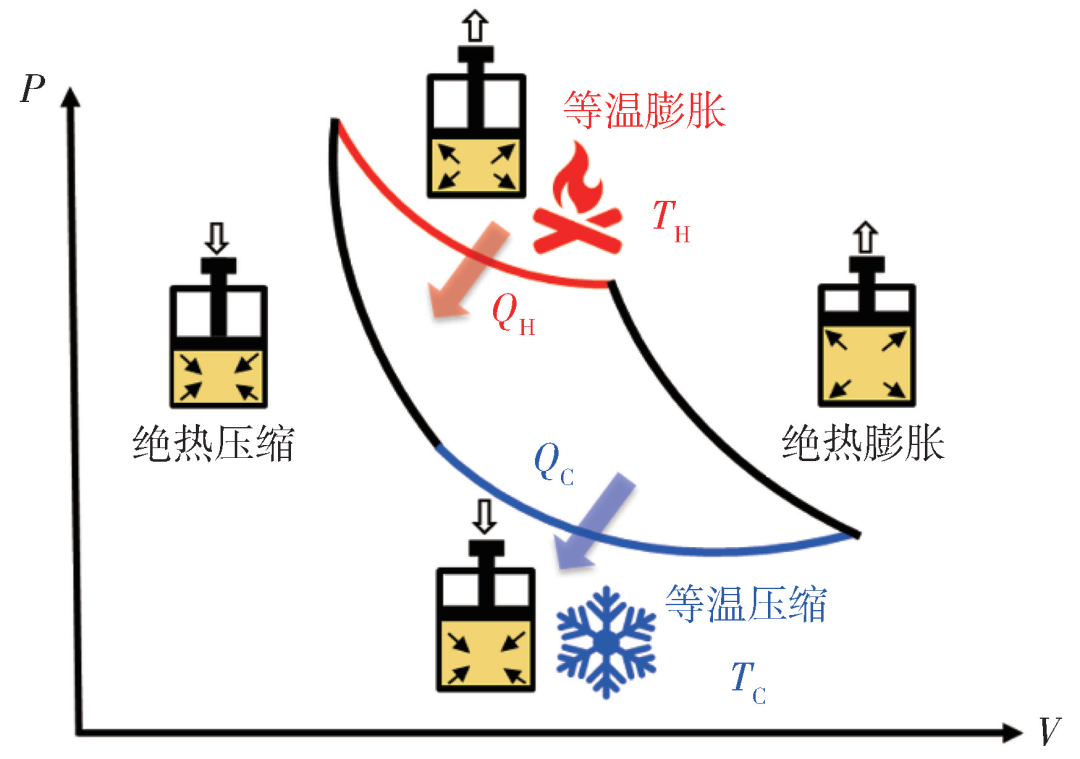
对于热机而言，功率和效率是衡量其性能的两个主要参数：功率表示单位时间内热机对外做功的多少，效率代表热机能以多大的比例将从高温热源吸收的热量转化为可用的输出功。从18世纪直至19世纪初，受到热力学发展制约，人们在理论上研究的主要是工作在准静态 (参数变化足够缓慢、时时刻刻几乎达到平衡态) 循环中的理想热机。萨迪·卡诺的研究给出了这样一种理想的热机效率的上限，即著名的卡诺效率[1]：


其中 TC 和 TH 分别是热机所接触的低温热源与高温热源的温度。要实现这一效率，需要热机在卡诺循环中准静态( t → ∞ )地工作，如图2所示。对于工作在准静态热力学循环中的可逆热机而言，其热功转换率，即效率，虽然能达到卡诺效率，但准静态意味着热机单位时间的输出功趋于 0，即功率 P ⇌ W/t → 0 。在这种极限情况下，热机虽然高效，但没有实际的用处，只能用作理想模型研究平衡态循环。从19世纪到20世纪初期，经典热力学已经对平衡态和可逆过程给出相当完整的描述，提供了许多适用于平衡态热力学量的关系。长期以来，这些关系对物理、化学和工程中热力学的研究起着重要的作用。

图2 以理想气体为做功物质的可逆卡诺循环示意图。这一循环需要在准静态条件下实现，其输出效率就是卡诺效率ηC=1-TC/TH


虽然经典热力学中的一些基本定律 (如热力学第二定律)，是用不可逆过程表达出来的，但经典热力学集中于研究平衡态系统。然而，实际的热力学过程绝大多数是不可逆过程，系统在经历这些过程时一般处在非平衡态。为了研究不可逆过程中热力学系统的非平衡效应，20世纪30年代热力学的发展从平衡态拓展到非平衡态。在此期间，有限时间热力学理论得以发展，人们开始在理论上研究更接近现实的实际热机：在偏离准静态假设的有限时间的热力学循环中运行的热机。在有限时间热力学循环中，热机的做功物质与热库的接触过程以及对外做功的过程均不再是准静态的可逆过程，可以实现非零的输出功率。热力学第二定律指出，热机在经历这样的热力学循环后会有不可逆的熵增。这部分熵增反映了热机在有限时间内工作而损耗的能量，这些能量不能用于对外做功，从而会降低热机的效率。因此，有限时间热力学过程的不可逆性导致的熵产生会直接影响热机的功率和效率。如何优化有限时间热力学循环使热机获得更佳性能成为驱动有限时间热力学领域发展的主要研究动机[2,3]。

最近，我们在关于有限时间热力学过程的不可逆性熵产生与功率—效率约束关系的系列理论研究工作的基础上[4,5]，搭建了一个关于有限时间热力学的“实验热机”。在这一平台上，通过实验展示了有限时间等温过程中不可逆熵产生在长时区域与过程时间的反比关系[6]，并正在进一步的工作中探索完整的功率—效率约束的实验曲线。




2. 有限时间热力学与实际热机优化




有限时间热力学是经典热力学的延伸和推广，是20世纪30年代发展起来的不可逆热力学的一个新分支[2]。我们知道，经典热力学关心系统的热力学量由一个平衡态演化到另一个平衡态的变化，而不太关注不可逆热力学过程中的非平衡特征。然而，作为热力学过程的一个重要参数，时间在经典热力学中却没有被考虑，以致一些与热力学过程的动力学演化相关的重要问题未能得到解决。比如，在给定时间内，由一台热机对外输出一定的功需要从热源吸收的热量是多少？效率最高能达到多少？这都是经典平衡态热力学无法回答的问题。有限时间热力学也是现代热力学理论的一个交叉领域，是当前热工程应用的理论工具之一，主要研究非平衡系统在有限时间热力学过程中的能量传输和不可逆行为满足的规律[3]。在20世纪中叶，一些物理学家和工程师对核电站中的热能利用问题的思考启发了有限时间热力学的建立[7-9]。

20世纪50年代，法国物理学家伊冯 (J. Yvon) 率先研究了蒸汽机在热力学循环中功率的优化[7]，得到了在循环具有最大功率时的循环效率，也就是现在所谓的最大功率效率 (efficiencyatmaximumpower，EMP) 。这是一个有限时间热力学中描述热机性能的重要参量。以下，我们以伊冯所引入的有限时间热机模型 (伊冯模型) 为例，简要介绍有限时间热力学循环的优化过程。

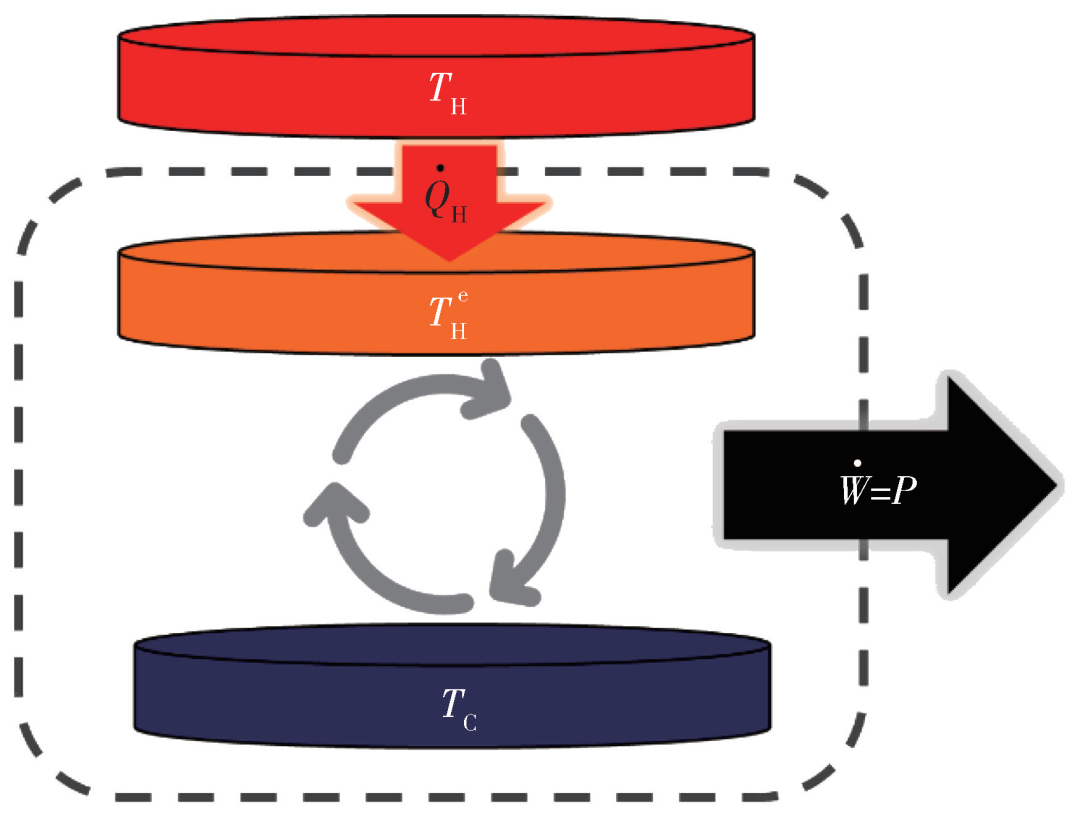
图3 伊冯内可逆卡诺热机示意图。伊冯热机工作在温度TH的高温热库和温度TC的低温热库间的卡诺循环中。在低温等温过程中，做功物质的温度为 TCe = TC ，而在高温等温过程中，做功物质的温度为 THe < TH 。 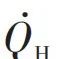是高温热库流向热机的热流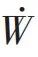，= P 是热机的输出功率


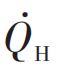如图3所示，伊冯研究的热机是一种内可逆的卡诺热机。该热机的工作物质，例如水蒸气，在卡诺循环的两个等温过程中分别与温度为 TH 的高温热库和温度为 TC 的低温热库接触。在低温端，假设做功物质能被足够快地冷却，于是其温度 TCe 与低温热库保持一致，即 TCe = TC ；在高温端，做功物质在等温过程中无法被足够快地热化而与热库保持热平衡接触，假设其具有小于热库温度的恒定温度 THe < TH 。在高温等温过程中，存在由温差导致的从热库流向做功物质的恒定热流。可以进一步假设这一热流满足牛顿传热定律，则有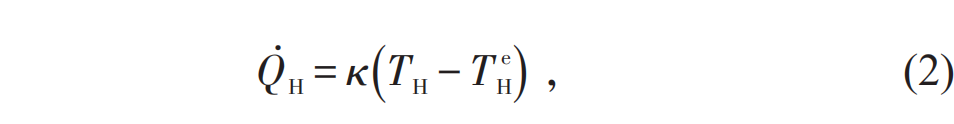


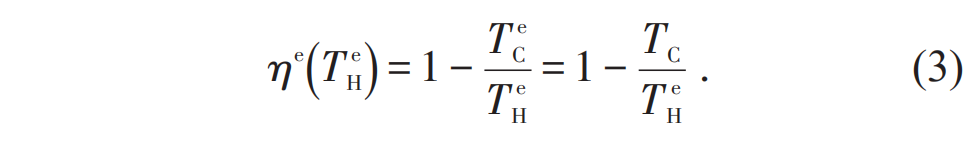
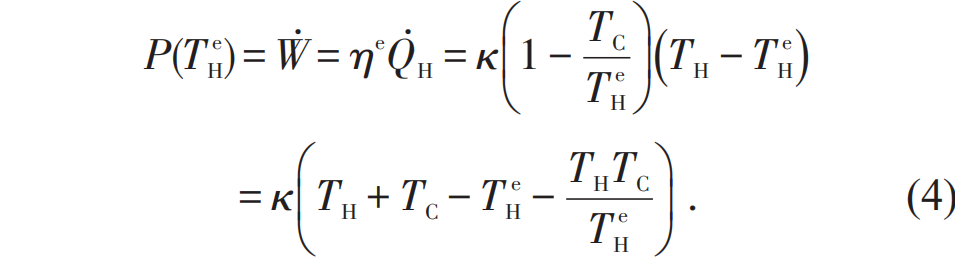
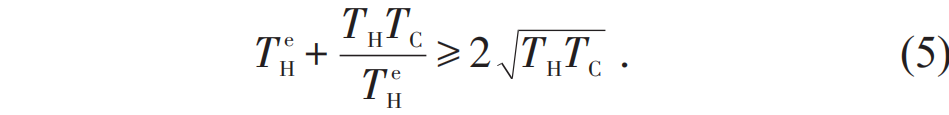
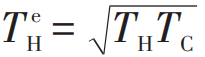其中 κ 是传热系数。另一方面，考虑热机内可逆 (Endo-reversible)，即热机工作在高温端和低温端温度分别为 THe 和 TCe 的可逆卡诺循环中。这里，内可逆意味着热机自身工作在一个等效的可逆卡诺循环中，而不可逆性仅来源于这一等效可逆卡诺循环中等温过程的温度与热库温度的温差导致的热流。这一内可逆循环的效率是由 THe 和 TCe 所决定的卡诺效率：


由此，这一内可逆卡诺热机的输出功率就是


伊冯将功率P 视为优化函数，THe视为优化参数。不难发现，上式括号中的最后两项满足均值不等式


当且仅当时(5)式取等号。将(5)式代入(4)式，即得到热机具有最大输出功率时的效率为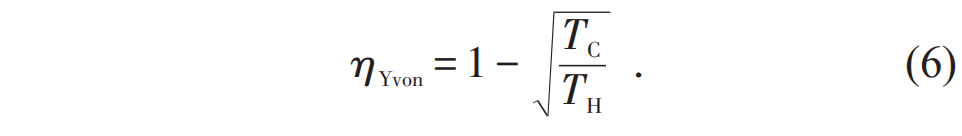


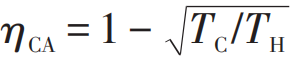这一效率明显低于卡诺效率。由于伊冯的文章是以法文撰写，这一结果在早期并未引起太多关注，但他关于热机优化的思想与此后该领域很多工作是一致的。

几乎同期，法国学者尚巴达尔 (P. Chambadal) [8]和前苏联核动力工程专家诺维科夫 (I. I. Novikov) [9]也分别研究了类似的问题，得到了与伊冯一致的结果。1975年，加拿大物理学家柯曾 (F. Curzon) 和艾尔邦 (B. Ahlborn) 用服从牛顿传热定律的内可逆热机模型研究了有限时间卡诺热机的优化问题[10]。他们同时考虑了热机在与高温热库和低温热库接触时的非平衡热流，得到了这一热机的最大功率效率 ，这就是著名的Curzon—Ahlborn (CA) 效率。需要注意的是，由于模型的相似性，CA效率和伊冯热机模型的最大功率效率形式一致。柯曾和艾尔邦的工作得到了广泛的关注，引领了有限时间热力学领域在此后几十年的蓬勃发展，一大批学者考察了各类实际热机在有限时间热力学循环中的运作，对它们的最大功率效率及其他工作特征进行了大量的研究[2,3]。

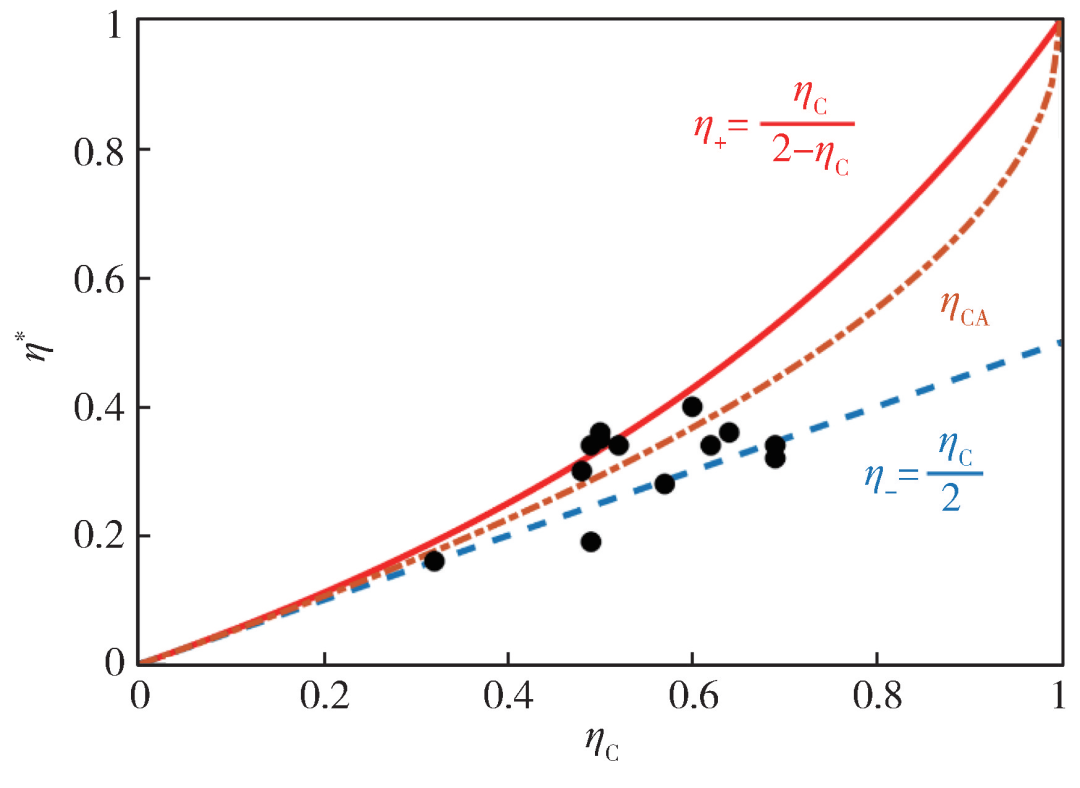20世纪80年代，厦门大学严子俊等最早将有限时间热力学引入国内，并在多类有限时间热力学循环的分析与优化问题上进行了较为系统的研究[11—14]。此后，中国人民解放军海军工程大学陈林根、孙丰瑞等在工程热力学的背景下在这一领域进行了有益的探索[15,16]。到了21世纪，人们从更基本的层面讨论了不同有限时间模型所描述的不可逆热机的最大功率效率[17]。例如，德布罗克 (C. Van den Broeck) 利用昂萨格关系讨论了线性不可逆热机的优化[18]；在随机热力学的框架下，施米德尔 (T. Schmiedl) 和塞弗尔特 (U. Seifert) 研究了以布朗粒子为做功物质的热机[19]，并得到了其最大功率效率的一般表示；涂展春研究了费曼棘轮的功率在有限时间中的优化[20]，并分析了费曼棘轮的最大功率效率关于卡诺效率展开形式的普适性。另外，通过引入有限时间等温过程中不可逆熵产生的时间反比关系，埃斯波西托 (M. Esposito) 等人讨论了低耗散类卡诺热机的最大功率效率，并得到了最大功率效率满足的普适的上下界[21]。

图4 最大功率效率(EMP) η* 所满足的关于卡诺效率 ηC 的上下界[21]。图中红色实线和蓝色虚线分别是 EMP 的上界η+ = ηC/(2 – ηC) 和下界 η– = ηC/2 ，橘黄色点虚线是 CA 效率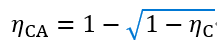。黑色数据点是文献[21]引用的当时世界上运行的一些核电站中热机效率的实验结果


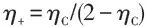图4给出埃斯波西托等人得到的最大功率效率满足的普适的上下界，这是一个产生了较大影响的结果。因为他们给出的上界 和下界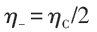能将此前不同有限时间热机模型得到的最大功率效率都包含在内，比如图4中橘黄色点虚线代表的CA效率。同时，这一组上下界也可以较好地涵盖已有的一些实验结果，是另一个相对普适的结果[21]。这些有限时间热机模型的出现引发了21世纪对实际热机优化的丰富研究，也启发了人们对有限系统的非平衡热力学的深入探索。




3. 热机的功率—效率约束关系

和不可逆熵产生




尽管此前大量研究已经对不同类型热机的最大功率效率进行了细致的讨论[17]，但是仍有一个问题尚未解决：功率和效率之间是否存在更一般的约束关系？是否能基于此关系对给定功率下的效率进行优化？有限时间热力学的研究表明，优化热机功率和效率的关键在于分析热机在工作中由不可逆熵产生表征的不可逆能量耗散对工作时间的依赖关系[17,19,21]。然而，有限时间热力学已经广泛研究的最大功率效率只是将功率作为优化函数取得其极大值后所得到的热机效率这一种特殊情况。在更一般的情形中，我们需要根据具体目标来对功率和效率，或者它们二者组成的某些优化函数进行联合优化。比如，只从最大功率效率出发，无法得知热机在给定功率的最大效率，或者给定效率下的最大功率。这种情况下，就需要分析在熵产生所描述的不可逆性的约束下，热机的功率效率之间的基本约束关系。

为了更直观地理解这一问题，我们来想象一个马车运水的情景，如图5所示，利用马车上的开口容器从水源地把水运输到城市。由于马车运送过程的颠簸，水在运输途中会从开口容器中洒落一部分出来，马车走得越快，溢出的就越多。显然为了减少运输损耗，需要尽量降低运动速度，但是这种情况下给定时间内运输的水量就会减少。具体来说，可以把马车一趟的运送水量叫做单位时间运水量，每次从水源地载入的总水量A与实际到城市的水运输量B之比B/A叫做运输效率。从这个简单的例子可以看出，单位时间运水量和运输效率间存在着一定的约束关系，这一约束关系是由运输途中损失的水量与运输时间相关而导致的。

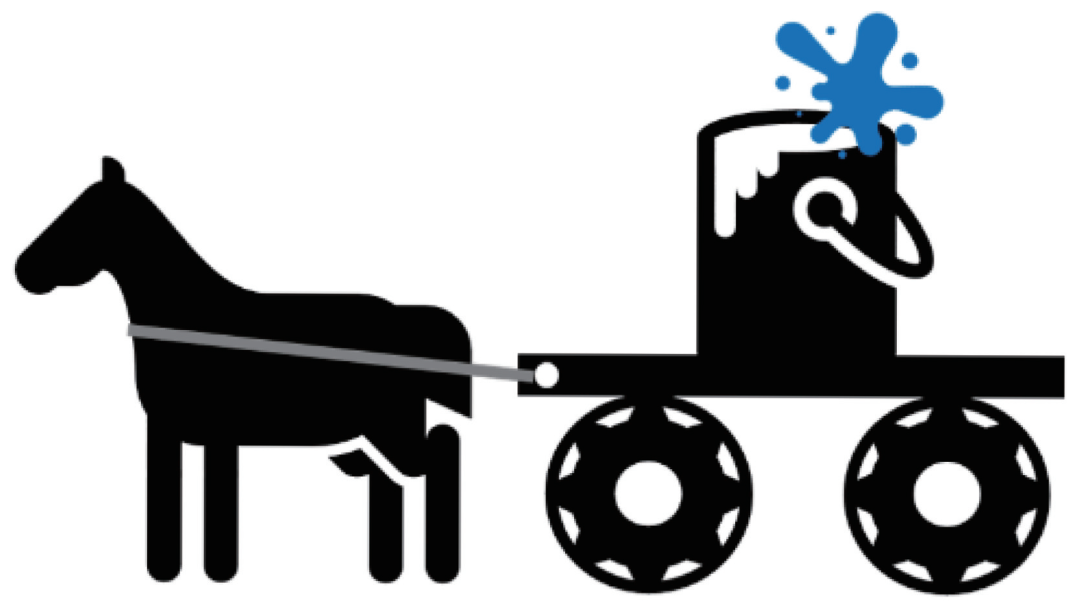
图5 马拉车运水示意图。由于颠簸，马车运水时会有水洒出，洒出的水量与颠簸的程度或者运输的速度快慢有关。这一情景可以类比热力学过程中不可逆熵产生带来的热耗散


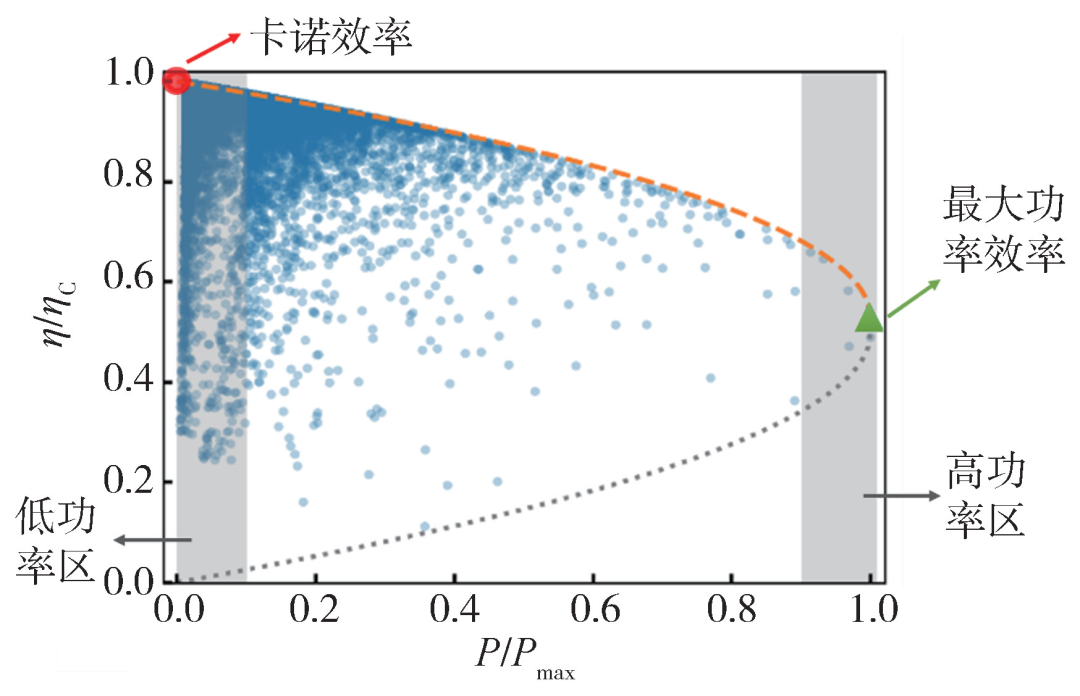
上述例子中我们引入的运输效率和单位时间运水量正好对应于热机的效率和功率。运输途中损失的水量，代表热机在有限时间内工作而损耗的能量，这一部分能量不能用于对外做功，因而会降低热机的效率。正是由于在运行过程中的能量损失 (耗散)，热机的功率和效率之间存在着一定的约束关系。显然，这一约束关系对设计针对具体生产任务的最优热机十分重要，引起了广泛的研究兴趣[4,22—25]。其中，从低耗散热机模型[21]出发，霍鲁贝克 (V. Holubec) 和里亚博夫 (A. Ryabov) 在热机的低功率区和最大功率附近 (图6中灰色区域)，近似得到了功率效率的约束关系，并从数值上验证了这一关系[22]；最近，我们用解析方法在低耗散热机的整个参数区发现了功率效率的一般约束关系[4]，并发现二能级原子热机在有限时间热力学循环中的性能可以很好地被这一约束关系所描述，如图6所示。

图6 热机的功率效率约束关系[4]。纵轴是用卡诺效率归一化后的效率，横轴是以循环的最大功率无量纲化并归一化后的功率。图中的橘色虚线和灰色点线分别是功率效率约束关系的上界和下界，蓝色点是模拟二能级热机工作给出的功率—效率数据。绿色三角区域和红色点分别代表最大功率效率和卡诺效率。文献[22]研究了在灰色区域所代表的相对最大功率的低功率区和高功率区中的功率效率约束关系


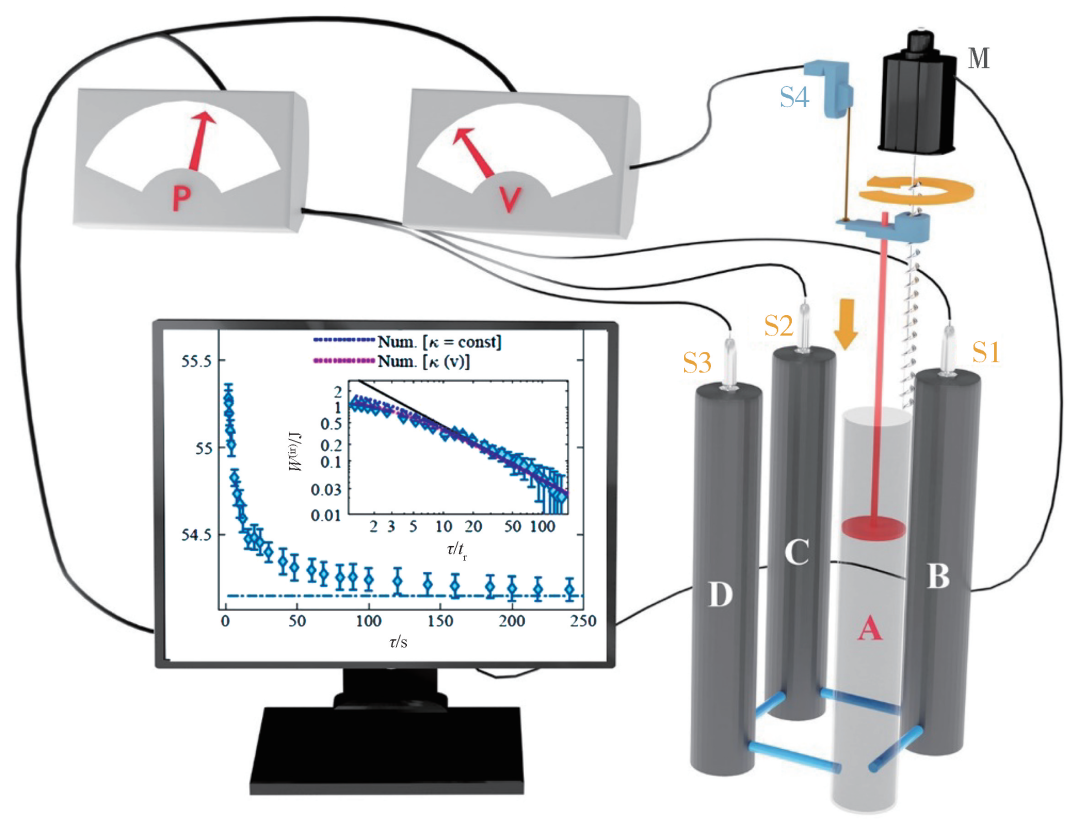
在图6中，红色点对应的区域热机的效率趋近卡诺效率而功率为 0，此时热机工作在准静态的循环中，即经典热力学所关心的平衡态区域。绿色三角形标出的是热机最大功率效率所在的位置。我们的工作表明，在热机的功率从0取到最大值之间时，功率、效率之间的确存在一个约束关系，其上下界分别由橘色虚线和灰色点线给出。这样一来，热机的工作区间就被限制在了图中两组虚线所包围的区域内。基于这样的约束，就可以根据具体需求研究在任意给定的关于功率和效率的优化函数下热机的优化问题了。至此，我们回答了本节一开始提出的问题，热机的功率和效率之间确实存在一般性的约束关系。值得一提的是，功率效率的基本约束关系告诉我们，不可能造出功率和效率同时取到极大值的热机。但是，功率和效率也不像孟子笔下的鱼和熊掌那样不可兼得。在这一基本约束范围内，可以根据具体目标尽可能寻求功率和效率的最优权衡，即在享有“熊掌”的同时也能品尝“鱼”的美味。

如前文所述，热力学循环的不可逆性对热机功率和效率的约束关系及优化至关重要，这一不可逆性可以用不可逆熵产生来表征：越多的不可逆熵产生意味着越强的不可逆性，反之亦然。在不同模型和系统中的理论研究都表明，在有限时间等温过程中，不可逆熵产生在长时区域与过程时间恰好成反比[4—6,19,21,26,27]，这是一个十分简洁也非常有用的关系，被广泛用于不同的热力学优化中。然而，我们注意到，一直以来都缺乏对这一关系定量的实验研究。

图7 右：测量不可逆功的实验装置示意图[6]。干燥空气被封存在4个相互连通的气缸A—D中，这些气缸被置于一个可以控制温度的恒温水浴环境中。其中A气缸的活塞可以用由电脑控制的步进电机推动来实现对气体的可控压缩。气体的压强P和体积V分别由压强传感器和位移传感器测得；左：在水浴温度为40℃时对气体不同压缩速度下测得的做功随压缩时间的关系(压缩距离固定)。其中蓝色菱形点为实验结果，蓝色点虚线为准静态情况下的做功。子图为不可逆功W(ir) ，即做功与准静态做功(自由能变化)的差，关于压缩时间τ的对数坐标图。可以看出，在长时区域不可逆功与时间成反比关系，与黑色实线代表的长时区域的理论结果符合较好


最近，如图7所示，我们设计并搭建了一个实验平台[6]：将干燥空气置于可压缩的气缸里并整体沉浸在温度( Te )可控的恒温水浴中，利用步进电机控制压缩气体的活塞实现可控压缩。通过气缸上装载的压强传感器和与活塞相连的位移传感器，我们能以较高精度分别测量气缸内气体的压强 P 和体积 V 。对于给定的压缩距离，通过改变步进电机的压缩速度，可以得到不同压缩时间(τ)下气体的 P – V 曲线。根据气体对外做功的定义 W = -∫PdV ，基于测得的 P – V 曲线得到了不同时间内压缩气体做的功 (图7中蓝色数据点)。最终给出了不可逆功 W(ir) = W – ∆F 对过程时间的依赖关系，如图7左侧图中子图所示。这里，不可逆功 W(ir) 是过程所做功 W 和自由能变化 ∆F (准静态过程做功) 的差，在长时区与不可逆熵产生 ∆S(ir) 成正比，即 W(ir) = Te∆S(ir)。基于对不可逆功的测量，我们首次检验了有限时间等温过程中长时区域的不可逆熵产生 ∆S(ir) 和过程时间 τ 的反比关系：∆S(ir) ∝1/τ [6]。实验结果表明，除了与过程时间成反比外，我们感兴趣的这一不可逆熵产生还可以通过压缩空气的方式来改变。比如，在压缩时间和其他条件一定的情况下，匀速地压缩和先慢后快地压缩气体，所测得的不可逆功是不同的。这意味着可以通过改变对做功物质的操纵方式来有效地调节有限时间热力学过程的不可逆性，为设计最优的有限时间热机提供了新的思路。值得一提的是，这一操纵方式依赖的不可逆熵产生在微观尺度依然成立，我们在最近关于量子热机的理论工作中对此进行了详细研究[5]。




4. 从有限时间热力学到量子热力学




本文概述了有限时间热力学的发展及现状，特别是最近在有限时间热机功率效率约束关系上的研究，以及我们对于有限时间等温过程中不可逆性的时间反比行为的研究。总的来说，在理论方面，有限时间热力学是非平衡热力学的重要分支，其研究成果对理解热力学过程中的不可逆性十分关键；在应用方面，有限时间热力学主要用于解决实际生产中热力学循环的优化问题，在热力工程领域有重要的指导意义。除前面提到的最大功率效率以及功率效率约束关系外，热力学非平衡过程的几何描述与优化[28—30]、有限时间热力学过程及热机循环的最优控制与操纵[5,6,31-36]、热力学不确定关系[37,38]、有限热源间热机的优化[39,40]、以及有限时间内信息处理的能量消耗[41,42]等也是近年来有限时间热力学领域在理论上关注的热点研究问题。同时，除了前面介绍的我们关于不可逆熵产生的实验[6]，最近也有一些实验报道了对有限时间热力学中的其他理论预言，如最大功率效率[43]、等温捷径[44]等的检验。

从20世纪后期至今，除了研究非平衡热力学系统或过程的有限时间热力学效应，热力学的发展还与量子力学结合起来衍生出了一个新的分支：量子热力学[45—48]。这一领域旨在探究量子效应引起的微观系统的非平衡热力学行为。需要注意的是，只有对于偏离热力学极限 (经典极限) 的小系统而言，量子效应才会有用武之地。量子热力学研究热点之一便是讨论一系列的量子效应，如能级离散、量子相干性、量子纠缠和量子相变等对热力学量或热力学过程的影响，以及是否有利于提高由量子系统构造的热机的性能。近20年，这一领域吸引了国内外相当高的研究兴趣，也在理论和实验上均取得了一系列有意义的结果[48—59]。而在量子热力学的框架内讨论有限时间的热力学过程与热机的优化，也是最近备受关注的方向[4,5,33—36,60]。最近，美国白宫量子协调办公室发布了《国家量子信息科学战略投入的量子前沿报告》，系统勾画了其心目中的量子科技前沿，其中特别提到如何利用量子资源实现量子热力学的新效应[61]。

众所周知，不可逆性是区分有限系统的非平衡热力学与平衡态热力学的关键。在本文第3节中，我们在实验上研究的不可逆熵产生局限于长时区域，或者说近平衡区域。作为不可逆性的度量之一，不可逆熵产生在远离平衡区 (长时区域) 的更多丰富行为值得进一步研究。我们此前的实验[6]已经发现了在短时区域的不可逆熵产生偏离了其在长时区域所满足的时间反比标度律。这一偏离的具体特征对设计最优的有限时间热力学循环有直接影响，需要理论上的深入探索[62]。从另一个方面看，对于由量子力学所描述的满足幺正演化的孤立系统，由其密度矩阵ρ所确定的冯·诺依曼熵 S=-tr(ρlnρ) 是不随时间改变的，即系统的熵或者说信息是守恒的。而在绝大多数情况下，我们所关心的系统都会不可避免地与环境和测量仪器耦合，成为开放量子系统[63]。这种情况下，系统的熵将会伴随着在环境中的演化过程发生改变。首先，环境和测量导致的退相干都会给系统带来熵增；其次，环境与系统的能量交换带来的热化也会带来熵增。前者是导致系统相干性降低带来信息丢失 (实为系统与环境的信息关联) 的原因，后者是导致系统热力学熵增加的原因。分析清楚在与环境的不同耦合方式下熵增现象在不同时间尺度的行为，对设计一系列量子器件都具有重要作用。

例如，设计量子计算机需要避免计算过程中物理比特和环境耦合引起的退相干的发生。这其实是在避免与信息丢失相关的熵增对应的不可逆过程的出现，否则将会导致量子计算优势的丧失；再者，在量子传感中需要避免熵增，与环境相互作用导致的热化过程中的热涨落会降低对信号的探测精度；另外，对量子热机的优化需要能操控热力学循环中的不可逆性，即在原理允许的范围内实现热机高功率运行的同时尽可能减少能量损失。未来，在微观尺度下乃至量子区域讨论有限时间热力学过程中的能量传输、不可逆耗散、信息关联等问题是一个非常值得关注的发展方向，这会帮助我们深入理解原子尺度系统的非平衡热力学效应，也会为设计能在量子世界里工作的高性能器件打下理论基础。

致 谢  感谢课题组成员袁红和岳鑫对本文的细致阅读与建议。


参考文献

[1] Huang K. Statistical Mechanics(2nd). New York：John Wiley & Sons，1987

[2] Andresen B，Salamon P，Berry R S. Physics Today，1984，37(9)：63；J. Chem. Phys., 1977，66 (4)：1571

[3] Bejan A. Advanced Engineering Thermodynamics. New York：Wiley，1988

[4] Ma Y H，Xu D，Dong H et al. Phys. Rev. E，2018，98：042112

[5] Ma Y H，Xu D，Dong H et al. Phys. Rev. E，2018, 98, 022133

[6] Ma Y H，Zhai R X，Chen J F et al. Phys. Rev. Lett., 2020，125：210601

[7] Yvon J. In: Proceedings of the International Conference on Peaceful Uses of Atomic Energy. Geneva：United Nations，1955. p. 387

[8] Chambadal P. Les Centrales Nuclaires. Paris：Armand Colin，1957

[9] Novikov I. J. Nucl. Energy，1958，7：125

[10] Curzon F，Ahlborn B. Am. J. Phys., 1975，43：22

[11] 严子浚. 物理，1984，12：768

[12] 严子浚. 工程热物理学报，1985，1：1

[13] 陈丽璇，严子浚. 自然杂志，1987，11：825

[14] 陈金灿，严子浚. 厦门大学学报(自然版)，2001，40：202

[15] 孙丰瑞，陈林根，陈文振. 热能动力工程，1989，2：1

[16] 陈林根，孙丰瑞，陈文振. 热能动力工程，1989，2：7

[17] Tu Z C. Chinese Phys. B，2012，21：020513

[18] Van den Broeck C. Phys. Rev. Lett.，2005，95：190602

[19] Schmiedl T，Seifert U. Europhys. Lett., 2008，81：20003

[20] Tu Z C. J. Phys. A，2008，41：312003

[21] Esposito M，Kawai R，Lindenberg K et al. Phys. Rev. Lett.,2010，105：150603

[22] Holubec V，Ryabov A. J. Stat. Mech., 2016，7：073204

[23] Proesmans K，Cleuren B，Van den Broeck C. Phys. Rev. Lett.,2016，116：220601

[24] Shiraishi N，Saito K，Tasaki H. Phys. Rev. Lett., 2016，117：190601

[25] Pietzonka P，Seifert U. Phys. Rev. Lett., 2018，120：190602

[26] Salamon P，Nitzan A，Andresen B et al. Phys. Rev. A，1980，21：2115

[27] Cavina V，Mari A，Giovannetti V. Phys. Rev. Lett., 2017，119：050601

[28] Crooks G E. Phys. Rev. Lett., 2007，99：100602

[29] Sivak D A，Crooks G E. Phys. Rev. Lett., 2012，108：190602

[30] Abiuso P，Miller H J D，Llobet M P et al. Entropy，2020，22：1076

[31] Tu Z C. Phys. Rev. E，2014，89：052148

[32] Li G，Quan H T，Tu Z C. Phys. Rev. E，2017，96：012144

[33] Dann R，Tobalina A，Kosloff R. Phys. Rev. Lett., 2020，122：250402

[34] Chen J F，Sun C P，Dong H. Phys. Rev. E，2019，100：032144

[35] Chen J F，Sun C P，Dong H. Phys. Rev. E，2019，100：062140

[36] Pancotti N，Scandi M，Mitchison M T et al. Phys. Rev. X，2020，10：031015

[37] Pietzonka P，Ritort F，Seifert U. Phys. Rev. E，2017，96：012101

[38] Horowitz J M，Gingrich T R. Phys. Rev. E，2017，96：020103

[39] Izumida Y，Okuda K. Phys. Rev. Lett., 2014，112：180603

[40] Ma Y H. Entropy，2020，22：1002

[41] Proesmans K，Ehrich J，Bechhoefer J. Phys. Rev. Lett., 2020，125：100602

[42] Miller H J D，Guarnieri G，Mitchison M T et al. Phys. Rev. Lett.,2020，125：160602

[43] Martínez I A，Roldán É，Dinis L et al. Nat. Phys., 2015，12：67

[44] Albay J A C，Wulaningrum S R，Kwon C et al. Phys. Rev. Research，2019，1：033122

[45] Kosloff R，Levy A. Annu. Rev. Phys. Chem., 2014，65：365

[46] Binder F，Correa L A，Gogolin C et al. Thermodynamics in the Quantum Regime. Springer International Publishing，2018

[47] 孙昌璞，全海涛，董辉. 量子信息启发的量子统计和热力学若干问题研究.见：龙桂鲁，邓富国，曾谨言. 量子力学新进展(第五辑). 北京：清华大学出版社，2011

[48] Quan H T，Liu Y，Sun C P et al. Phys. Rev. E，2007，76：056110

[49] Quan H T，Zhang P，Sun C P. Phys. Rev. E，2005，72：056110

[50] Dong H，Xu D Z，Cai C Y et al. Phys. Rev. E，2011，83：061108

[51] Brandão F G S L，Horodecki M，Oppenheim J et al. Phys. Rev.Lett., 2013，111：250404

[52] Uzdin R，Levy A，Kosloff R. Phys. Rev. X，2015，5：031044

[53] Xu D Z，Wang C，Zhao Y et al. New J. Phys., 2016，18：023003

[54] Ma Y H，Su S H，Sun C P. Phys. Rev. E，2017，96：022143

[55] Su S H，Chen J F，Ma Y H et al. Chin. Phys. B，2018，27：060503

[56] Camati P A，Santos J F G，Serra R M. Phys. Rev. A，2019，99：062103

[57] Roßnagel J，Abah O，Schmidt- Kaler F et al. Phys. Rev. Lett.,2014，112：030602

[58] Deng S，Chenu A，Diao P et al. Science Advances，2018，4：eaar5909

[59] Peterson J P S，Batalhão T B，Herrera M et al. Phys. Rev. Lett.,2019，123：240601

[60] Dann R，Kosloff R，Salamon P. Entropy，2020，22：1225

[61] The White House National Quantum Coordination Office, Quantum frontiers report on community input to the nation’s strategy for quantum information science, https://www.quantum.gov/wpcontent/uploads/2020/10/QuantumFrontiers.pdf

[62] Ma Y H，Sun C P，Dong H. Self-consistency of optimizing finitetime Carnot engines with the low-dissipation model.arXiv:2012.08748

[63] 孙昌璞. 物理，2010，39(1)：1


参考文献可上下滑动查看


非平衡统计物理读书会启动！


2024年诺贝尔物理学奖授予人工神经网络，这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象，还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来，复杂现象如何涌现。它通过研究大量粒子的集体行为，成功地将微观世界的随机性与宏观世界的确定性联系起来，为我们理解自然界提供了强大的工具，也为机器学习和人工智能领域的发展提供了重要推动力。


为了深入探索统计物理前沿进展，集智俱乐部联合纽约州立大学石溪分校教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学助理教授唐乾元（傅渥成），共同发起「非平衡统计物理」读书会，关注非平衡统计物理的前沿理论、生命和热力学、统计物理与机器学习交叉三个大的主题方向，涵盖热机优化问题、涨落相关的热力学、反常热力学现象、信息视角下的热力学、生命系统的景观和流理论、活性物质、生命系统、种群动力学、机器学习和人工智能等前沿话题。我们诚挚邀请相关领域的研究者分享工作，也欢迎感兴趣的朋友们一起参与讨论交流！（扫描下图中二维码报名）



详情请见：从热力学、生命到人工智能的统计物理之路：非平衡统计物理读书会启动！



推荐阅读

1. Physics Reports 速递：量子热机和量子冰箱
2. 从热力学第二定律到第四定律：关于物理、生命、信息、认知的大统一理论
3. 热力学如何解释进化论：最大化熵产生原理驱动下的自然选择
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 龙年大运起，学习正当时！解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！



点击“阅读原文”，报名读书会