因果涌现第六季——动力学、因果抽象与信息分解

导语
在霓虹灯的闪烁、蚁群的精密协作、人类意识的诞生中,隐藏着微观与宏观之间深刻的因果关联——这些看似简单的个体行为,如何跨越尺度,涌现出令人惊叹的复杂现象?因果涌现理论为我们揭示了答案:复杂系统的宏观特征无法通过微观元素的简单叠加解释,而是源于多尺度动态交互中涌现的因果结构。从奇异值分解(SVD)驱动的动态可逆性分析,到因果抽象与信息分解的量化工具,研究者们正逐步构建起一套跨越数学、物理与信息科学的理论框架,试图解码复杂系统的“涌现密码”。
为了系统梳理因果涌现最新进展,北京师范大学系统科学学院教授、集智俱乐部创始人张江老师领衔发起「因果涌现第六季」读书会,组织对本话题感兴趣的朋友,深入研读相关文献,激发科研灵感。
读书会将从2025年3月16日开始,每周日早9:00-11:00,持续时间预计10周左右。每周进行线上会议,与主讲人等社区成员当面交流,之后可以获得视频回放持续学习。诚挚邀请领域内研究者、寻求跨领域融合的研究者加入,共同探讨。
读书会背景
读书会背景
读书会框架
读书会框架
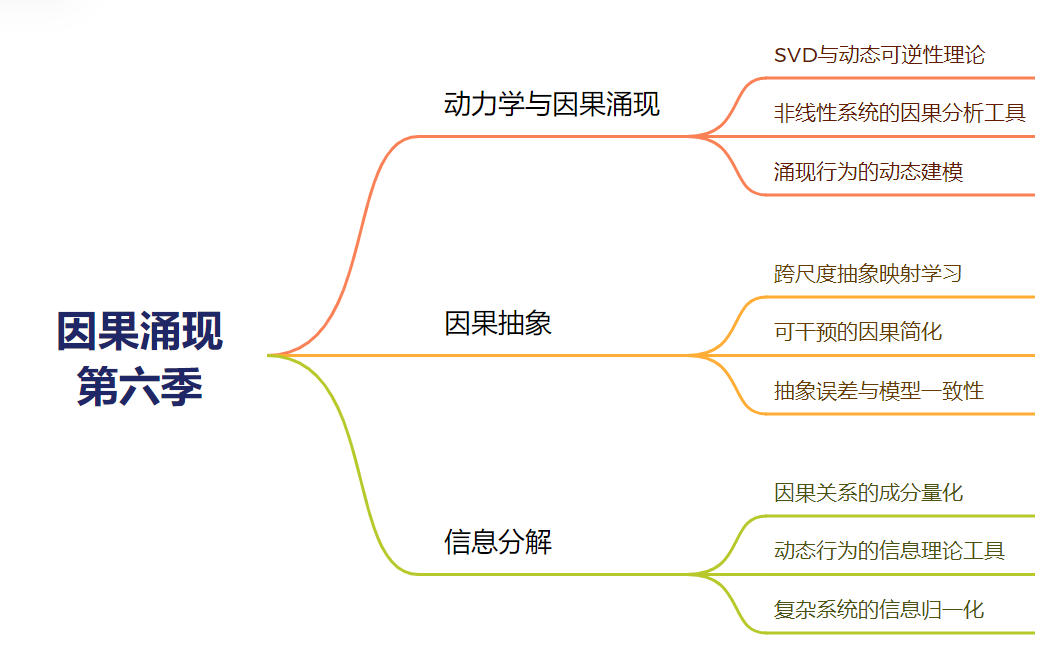
此次读书会分成以下几个部分,分别为动力学与因果涌现、因果抽象、信息分解。读书会发起人已经收集了这几个方向的大量文献。我们希望通过各个部分的文献阅读,能够对因果涌现有一个更加全面的了解,也期待更多感兴趣的研究者能够在这片方兴未艾的研究领域找到未来的科研方向。
发起人团队
发起人团队
张江,北京师范大学系统科学学院教授,集智俱乐部、集智学园创始人,集智科学研究中心理事长,曾任腾讯研究院、华为战略研究院等特聘顾问。主要研究领域包括因果涌现、复杂系统分析与建模、规模理论等。
个人主页:https://jake.swarma.org/

袁冰,集智科学研究中心技术与产品顾问。研究兴趣包括因果推断、复杂科学,以及人工智能相关领域。

王志鹏,北京师范大学在读博士。研究兴趣包括复杂网络与机器学习、因果涌现。

刘凯威,北京师范大学在读硕士。研究兴趣包括风险模型与生存分析、复杂网络重构、贝叶斯统计、因果涌现。

报名参与读书会
报名参与读书会
运行模式
从2025年3月16日开始,每周日早9:00-11:00,持续时间预计 10 周左右,按读书会框架设计,每周进行线上会议,与主讲人等社区成员当面交流,会后可以获得视频回放持续学习。
参与方式
此次读书会采用腾讯会议线上进行(请提前下载安装)。在扫码完成报名并添加负责人微信后,负责人会将您拉入交流社区(微信群),入群后告知具体的会议号码。
报名方式
第一步:扫码填写报名信息。

扫码报名(可开发票)
第二步:填写信息后,付费报名。
如需用支付宝支付,请在PC端进入读书会页面报名支付:
https://pattern.swarma.org/study_group/60
第三步:添加运营负责人微信,拉入对应主题的读书会社区(微信群)。
本读书会可开发票,请联系相关负责人沟通详情。
PS:为确保专业性和讨论的聚焦,本读书会谢绝脱离读书会主题和复杂科学问题本身的空泛的哲学和思辨式讨论;如果出现讨论内容不符合要求、经提醒无效者,会被移除群聊并对未参与部分退费。
针对学生的退费机制
读书会通过共学共研的机制,围绕前沿主题进行内容梳理和沉淀,所以针对于学生,可以通过参与共创任务,获取积分,积分达到退费标准之后,可以直接退费。
加入社区后可以获得的资源:
完整权限,包括线上问答、录播回看、资料共享、社群交流、信息同步、共创任务获取积分等。
参与共创任务获取积分,共建学术社区:
读书会采用共学共研机制,成员通过内容共创获积分(字幕修改、读书会笔记、论文速递、公众号文章、集智百科、论文解读等共创任务),积分符合条件即可退费。发起人和主讲人同样遵循此机制,无额外金钱激励。
阅读文献
阅读文献
阅读材料较长,为了更好的阅读体验,建议您前往集智斑图沉浸式阅读,并可收藏感兴趣的论文。

读书会文献阅读清单
动力学与因果涌现
-
Zhang, Jiang, et al. “Dynamical reversibility and a new theory of causal emergence based on SVD.” npj Complexity 2.1 (2025): 3. https://arxiv.org/pdf/2402.15054
提出一种基于奇异值分解(SVD)的因果涌现(CE)新理论框架,独立于具体的粗粒化方法来量化因果涌现,引入与 有效信息之间具有强相关性的“近似动态可逆性”的概念,为复杂系统的因果分析提供了新的视角。
-
Liu, Kaiwei, et al. “SVD-based Causal Emergence for Gaussian Iterative Systems.” arXiv preprint arXiv:2502.08261 (2025).
https://arxiv.org/abs/2502.08261
基于奇异值分解(SVD),用于高斯迭代系统(Gaussian Iterative Systems, GIS)的因果涌现(Causal Emergence, CE)量化框架,提供了一种不依赖于预定义粗粒化策略的因果涌现计算方法。
-
Wei, Tong, Weiyang Ding, and Yimin Wei. “Dual-Valued Functions of Dual Matrices with Applications in Causal Emergence.” arXiv preprint arXiv:2411.08377 (2024).
https://arxiv.org/pdf/2411.08377
基于双值函数和双矩阵量化因果涌现现象。
通过引入双值Ky Fan范数和双值过渡概率矩阵,研究解决了传统方法在处理奇异值无明显截断时的困难,为复杂系统的因果分析提供了新的理论和应用工具。
-
Crutchfield, James P. “The calculi of emergence: computation, dynamics and induction.” Physica D: Nonlinear Phenomena 75.1-3 (1994): 11-54.
https://www.sciencedirect.com/science/article/abs/pii/0167278994902739
提出一个基于分层ϵ-机器重构的归纳框架,通过分析有限推断资源如何推动新计算模型类的创新。
-
Ao, Ping. “Emerging of stochastic dynamical equalities and steady state thermodynamics from Darwinian dynamics.” Communications in theoretical physics 49.5 (2008): 1073.
https://iopscience.iop.org/article/10.1088/0253-6102/49/5/01/meta
探讨了达尔文动力学与热力学、统计力学之间的联系,指出达尔文动力学中的随机性暗示了温度的存在,从而导致了玻尔兹曼-吉布斯型的正则分布,并且热力学第二定律可以在没有详细平衡条件的情况下通过相对熵动态证明。
-
Yuan, Ruoshi, Ying Tang, and Ping Ao. “SDE decomposition and A-type stochastic interpretation in nonequilibrium processes.” Frontiers of Physics 12 (2017): 1-9.
https://link.springer.com/article/10.1007/s11467-017-0718-2
提出随机微分方程(SDE)分解方法和A型随机解释(A-type stochastic interpretation),用于分析非平衡过程中的动力学行为,揭示了复杂系统在噪声驱动下的稳定性、吸引子结构和演化特性。
-
Logožar, Robert, and Alen Lovrenčić. “The modeling and complexity of dynamical systems by means of computation and information theories.” Journal of information and organizational sciences 35.2 (2011): 173-196.
https://hrcak.srce.hr/file/111648
对计算力学更清晰的介绍。
-
Klus, Stefan, and Nataša Djurdjevac Conrad. “Dynamical systems and complex networks: A Koopman operator perspective.” arXiv preprint arXiv:2405.08940 (2024).
https://arxiv.org/pdf/2405.08940
探讨了koopman算子用于一般复杂动力学系统,简化为网络动力学的方法。
因果抽象
-
Invited talk: Fabio Massimo Zennaro: Introduction on Causal Abstraction
-
D’Acunto, Gabriele, et al. “Causal Abstraction Learning based on the Semantic Embedding Principle.” arXiv preprint arXiv:2502.00407 (2025).
https://arxiv.org/pdf/2502.00407
基于语义嵌入原则的因果抽象学习方法。
-
Zennaro, Fabio Massimo, et al. “Jointly learning consistent causal abstractions over multiple interventional distributions.” Conference on Causal Learning and Reasoning. PMLR, 2023.
https://arxiv.org/abs/2301.05893
提出一种基于结构因果模型(SCM)的因果抽象学习框架,通过联合学习多个干预分布之间的抽象关系,能在只知道部分抽象信息的情况下找到最优的因果抽象。
-
Felekis, Yorgos, et al. “Causal optimal transport of abstractions.” Causal Learning and Reasoning. PMLR, 2024.
https://arxiv.org/abs/2312.08107
通过引入多边际最优传输和因果约束,提出一种名为COTA(Causal Optimal Transport of Abstractions)的方法,用于从观测和干预数据中学习因果抽象映射,而无需完全了解底层因果模型。
-
Dyer, Joel, et al. “Interventionally Consistent Surrogates for Agent-based Simulators.” arXiv preprint arXiv:2312.11158 (2023).
https://openreview.net/pdf?id=UtTjgMDTFO
提出一种基于因果抽象理论的框架,用于构建复杂仿真模型的干预一致的替代模型,通过最小化抽象误差来确保替代模型在政策干预下的行为与原始模型保持一致。
-
Kekić, Armin, Bernhard Schölkopf, and Michel Besserve. “Targeted Reduction of Causal Models.” The 40th Conference on Uncertainty in Artificial Intelligence. 2023.
https://openreview.net/forum?id=CFHpI53xmb
通过引入信息论目标函数,提出了“目标因果简化”(Targeted Causal Reduction, TCR)方法,旨在将复杂的可干预模型简化为一组能够解释特定目标现象的因果因素。
信息分解
-
Martínez-Sánchez, Álvaro, Gonzalo Arranz, and Adrián Lozano-Durán. “Decomposing causality into its synergistic, unique, and redundant components.” Nature Communications 15.1 (2024): 9296.https://doi.org/10.1038/s41467-024-53373-4
提出一种新的因果推断方法,称为SURD(Synergistic-Unique-Redundant Decomposition),用于量化复杂系统中的因果关系。该方法通过将因果关系分解为冗余、独特和协同成分,能够有效捕捉变量之间的相互作用。
-
Yang, Mingzhe, Linli Pan, and Jiang Zhang. “Quantifying system-environment synergistic information by effective information decomposition.” arXiv preprint arXiv:2501.16676 (2025). https://arxiv.org/pdf/2501.16676
协同信息衡量系统在动态机制层面上对环境的灵活响应能力。
-
Faes, Luca, et al. “Predictive Information Decomposition as a Tool to Quantify Emergent Dynamical Behaviors In Physiological Networks.” arXiv preprint arXiv:2502.00945 (2025).
https://arxiv.org/pdf/2502.00945
提出一种基于信息理论的方法——预测信息分解(Predictive Information Decomposition, PrID),用于量化生理网络中动态行为的涌现特性。
-
Liardi, Alberto, et al. “Null models for comparing information decomposition across complex systems.” arXiv preprint arXiv:2410.11583 (2024).
https://arxiv.org/pdf/2410.11583
提出一种基于零模型(Null Model)的非线性归一化方法——NuMIT(Null Models for Information Theory),用于比较不同复杂系统中的信息分解。
-
Griffith, Virgil, and Christof Koch. “Quantifying synergistic mutual information.” Guided self-organization: inception. Berlin, Heidelberg: Springer Berlin Heidelberg, 2014. 159-190.
https://arxiv.org/pdf/1205.4265
综述了三种已有的信息论协同作用度量方法(Imax 协同度量(Smax)、整体减总和协同度量(WMS)、相关重要性(ΔI)),并提出了一种新的度量方法SVK。
-
Scagliarini, Tomas, et al. “Gradients of O-information highlight synergy and redundancy in physiological applications.” Frontiers in Network Physiology 3 (2024): 1335808.
https://doi.org/10.3389/fnetp.2023.1335808
O-information梯度能够有效识别生理网络中的协同和冗余信息。
相关主题读书会
相关主题读书会
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。而新兴的因果表征学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
集智俱乐部因果涌现读书会目前已经进行了四季。第一季读书会系统地梳理了因果涌现的概念,以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系,也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看:因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索。
第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合,包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。请参看:因果、涌现与机器学习:因果涌现读书会第二季启动。
第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行探讨和剖析,并详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。请参看:因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用。
第四季读书会主题是「新信息论:从分解到整合」,旨在系统梳理信息论领域的发展脉络,从信息熵的概念开始,逐步梳理各种信息测度的意义及其间的联系,深入理解信息整合与信息分解的本质,为跨学科应用做好准备。请参看:新信息论:从分解到整合|因果涌现读书会第四季启动。
第五季读书会追踪因果涌现领域的前沿进展,展示集智社区成员的原创性工作,希望探讨因果涌现理论、复杂系统的低秩表示理论、本征微观态理论之间的相通之处,对复杂系统的涌现现象有更深刻的理解。请参看:荟萃复杂系统前沿进展,集结因果涌现学术社区:因果涌现读书会第五季启动
因果涌现社区由集智俱乐部通过系列因果涌现读书会孕育孵化,旨在促进学术交流和科学创新,聚焦于破解复杂科学的圣杯问题,为国内学者和科学爱好者提供一个共享和探索的平台,推动科学研究的发展。
因果涌现系列读书会回放视频
现邀您加入「因果涌现读书会第六季」👇

点击“阅读原文”,报名读书会










