大模型向通用意识机器进化的关键——自指的启示
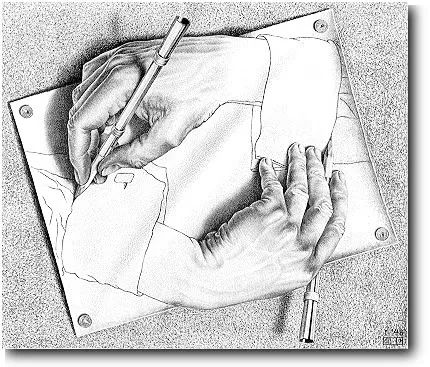
导语
自指(self reference)不仅可以构造悖论,导致图灵停机问题和哥德尔不完备性定理,同时也是生命自复制和意识机器最核心的部分。我们猜测,未来ChatGPT朝向通用意识机器进化,其中关键就是实现一个Quine结构。同时,随着类ChatGPT等AIGC内容的泛滥,人和机器的互动将陷入一种“图灵游戏”的模式,这种模式可以用于说明图灵停机问题的不可能性,也可以用于人机博弈——机器用一定规则产生内容,用户识别出这种规则,从而逼迫机器进入更深层次的规则创造。不断递归这种模式,机器将内在虚拟层不断深化,最终可能导致智能爆炸……
ChatGPT的一个研究方向就是让机器具备一定的自指能力,如自我提高(self improve),自我下命令(self instruction)。张江老师在集智俱乐部发起的大模型2.0读书会上详细的介绍了「从推断到自指」的主题分享,欢迎大家深入学习!
关键词:自指,递归定理,自复制自动机理论,生命自复制

张江 | 作者
1. 自指——一条永恒的金带
1. 自指——一条永恒的金带
自指是一个非常古老的话题,它通常与古代奥义以及各种神秘哲学有关。例如佛教中所提倡的“观身无常、观心无我”,以及古希腊的“认识你自己”,都在劝解人们能够将心智的观察箭头指向自己。中国道家所倡导的“无”,正是一个最简单的一字悖论。

自噬的蛇
一幅最能体现自指深邃含义的图画莫过于这条正在吞噬自己的蛇。此蛇作为一种图腾曾广泛出现在北欧神话、基督教神学、印度教和非洲宗教之中。这条蛇将自指那种深刻的自我毁灭性体现得淋漓尽致——我们可以想象一下当它把自己吞噬完毕会产生怎样怪异的情景。
将这种自我毁灭性的古代奥义应用到现代科学中已经产生了一系列深刻的结论。首先,在19世纪末,著名数学家康托尔(George Cantor)将“对角线删除”法则应用到集合论中,从而证明了实数的个数比自然数多。紧接着,罗素(Bertrand Russell)提出了著名的“罗素悖论”而摧毁了弗雷格(Gottlob Frege)的数学大厦。年仅25岁的哥德尔(Kurt Gödel)巧妙地应用同样的破坏性自指一举摧毁了数学大师希尔伯特(David Hilbert)的完备一致性的数学体系梦想。图灵(Alan Turing)则利用同样的技巧进一步发现任何超级计算机都不可能求解的图灵停机问题。
《纽约时报》曾将哥德尔不完备定理评价为20世纪最伟大的数学定理。自指可以用来构造破坏性的悖论已经是众人皆知、司空见惯了。然而,这种认识其实很片面。自指包含了比自指悖论更宽泛的内容,因为在自指大家庭中,还包括另外一类构建性的成员。
全文请参考:集智百科 | 系统中的观察者(5)——自指
https://wiki.swarma.org/index.php/系统中的观察者(5)——自指
实际上,早在1938年,与哥德尔共同奠定递归函数论基础的数学家克林尼(Stephen Kleene)就证明了递归函数论中的一个著名定理:递归定理(更精确地说,应该叫Kleene第二递归定理)。根据它,人们可以很轻松地得到一个数学推论,系统的自我复制是可能的。
证明递归定理的核心技巧,是一个被称为“蒯(kuai3)恩”的特别技术。蒯恩(Willard.V. Quine)是美国的哲学家,终身致力于哲学、数理逻辑、集合论的研究。他创造了一种称之为蒯恩的方法,使得人们可以不通过使用“我”或者“这句话”等词语就能创造出可以谈论自身的句子来。
有趣的是,蒯恩构造恰恰就是那条“黄金对角线”(这一方法正是当年康托尔最早提出证明实数比自然数多的方法,也是哥德尔定理构造哥德尔句子的关键技术)。只不过,康托尔、哥德尔等人的对角线与蒯恩的对角线方法稍有不同。我们会在第6节中详细地讨论这些技术。
2. 语言中的自指
2. 语言中的自指
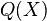 ,其中的
,其中的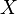 就是一个空穴,可以往其中添放任何一个句子。例如,如果我们让
就是一个空穴,可以往其中添放任何一个句子。例如,如果我们让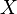 =“小明起床了”,那么原句子
=“小明起床了”,那么原句子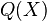 就成为了一个完整的句子:
就成为了一个完整的句子: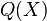 的意思对
的意思对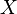 进行操作就得到了新句子
进行操作就得到了新句子 :
: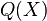 显然与
显然与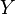 没有什么关系。
没有什么关系。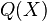 中的空穴
中的空穴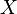 ,我们可以得到:
,我们可以得到: 。最关键的时刻来临了:我们让
。最关键的时刻来临了:我们让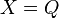 并代入
并代入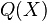 之中会怎样?也就是将除去空穴的句子部分
之中会怎样?也就是将除去空穴的句子部分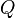 放到
放到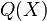 这个句子的空穴
这个句子的空穴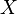 之中:
之中: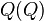 ,因为我们把空穴
,因为我们把空穴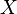 换成了残句子
换成了残句子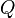 。之后,我们再按照这个句子所给出的使役动词进行操作,就能得到新句子
。之后,我们再按照这个句子所给出的使役动词进行操作,就能得到新句子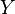 ,也就是:
,也就是: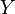 与原来的句子
与原来的句子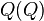 竟然是一模一样的!所以句子
竟然是一模一样的!所以句子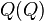 利用使役动词完成了“自复制”过程,也就是
利用使役动词完成了“自复制”过程,也就是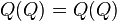 。
。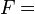 “得到的句子是假的”,并且把:
“得到的句子是假的”,并且把: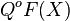 ,其中
,其中 符号表示将两个句子粘合在一起形成新的句子,于是
符号表示将两个句子粘合在一起形成新的句子,于是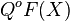 就是:
就是: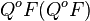 句子所描述的操作之后得到的句子跟
句子所描述的操作之后得到的句子跟 是一模一样的。所以这句话就相当于:“这句话是假的”。我们没使用“这句话”指代词就实现了自指。
是一模一样的。所以这句话就相当于:“这句话是假的”。我们没使用“这句话”指代词就实现了自指。
3. 建构性的自指
3. 建构性的自指
Print(‘helloworld!’)
Print(‘Print(’helloworld!’)’)
Print(‘Print(’Print(\’helloworld!\’)’)’)
S(x){ q=’S(x){\n q=\’’+q+’\’;\n
Print(\’’+p(q)+’\’);\n}’;
Print(‘S(x){n q=’’+q+’’;n Print(’’+p(q)+’’);n}’); }
A
B
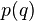 ,
,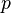 的作用是将字符串
的作用是将字符串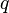 变换成更浅一层次的字符串。例如,如果
变换成更浅一层次的字符串。例如,如果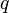 是“\’\’\n\”,那么
是“\’\’\n\”,那么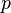 这个函数就会计算输出“’’n”。也就是说
这个函数就会计算输出“’’n”。也就是说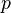 完成了一组映射:它把“\”映射成“”,把“’”映射成“’”,而把“n”映射成回车符。显然
完成了一组映射:它把“\”映射成“”,把“’”映射成“’”,而把“n”映射成回车符。显然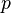 是可以写出来的。我们知道,由引号的引用可以形成更加深层次的虚拟世界(参见上一小节)。所以
是可以写出来的。我们知道,由引号的引用可以形成更加深层次的虚拟世界(参见上一小节)。所以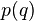 的作用就是让字符串
的作用就是让字符串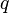 弹出一层虚拟世界。由于
弹出一层虚拟世界。由于 的作用很简单,我们假设它是一个系统自带的函数,因此就不在源代码1中给出
的作用很简单,我们假设它是一个系统自带的函数,因此就不在源代码1中给出 的实现代码了。
的实现代码了。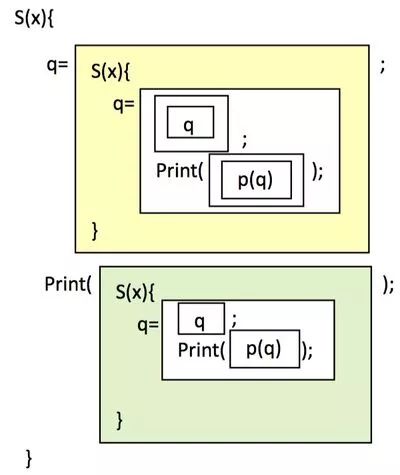
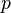 作用到
作用到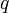 上面的结果即
上面的结果即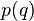 ;第五部分还是一个字符串:“’);n}”。然后当我们把q字符串的数值代入第二部分和第四部分,并进行运算
;第五部分还是一个字符串:“’);n}”。然后当我们把q字符串的数值代入第二部分和第四部分,并进行运算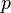 之后,就得到了和源程序一模一样的结果。你不妨在计算机上运行这段程序,就会发现这段程序会在屏幕上赤裸裸地把自己的源代码打印出来。
之后,就得到了和源程序一模一样的结果。你不妨在计算机上运行这段程序,就会发现这段程序会在屏幕上赤裸裸地把自己的源代码打印出来。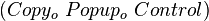 ,其中Copy就是5部分中的第二部分,即相当于一个拷贝字符串的程序,你输入 给Copy什么字符串,Copy就会把那个字符串再原封不动地吐出来;Popup这部分就是原来的5部分中的第四部分,即函数
,其中Copy就是5部分中的第二部分,即相当于一个拷贝字符串的程序,你输入 给Copy什么字符串,Copy就会把那个字符串再原封不动地吐出来;Popup这部分就是原来的5部分中的第四部分,即函数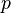 ,它的作用相当于一个弹出操作,也就是为输入的字符 串脱去一层引号。如果输入的字符串原来是在第
,它的作用相当于一个弹出操作,也就是为输入的字符 串脱去一层引号。如果输入的字符串原来是在第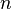 层虚拟世界,则Popup的作用就是让字符串跳到第
层虚拟世界,则Popup的作用就是让字符串跳到第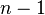 层;最后Control这部分就相当于原来的第1、3、5这三部分以及最一开始的语句Print的总合,它的作用就相当于是为Copy和Popup制造出来的字符添加适当的连接词,使得最后的字符串能够拼接成与原来的程序一模一样的源程序,并将其打印到屏幕上。所以这句“Print(‘S(x){nq=’’+q+’’;nPrint(’’+p(q)+’’);n}’);”就可以改写成
层;最后Control这部分就相当于原来的第1、3、5这三部分以及最一开始的语句Print的总合,它的作用就相当于是为Copy和Popup制造出来的字符添加适当的连接词,使得最后的字符串能够拼接成与原来的程序一模一样的源程序,并将其打印到屏幕上。所以这句“Print(‘S(x){nq=’’+q+’’;nPrint(’’+p(q)+’’);n}’);”就可以改写成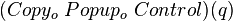 。其中“о”表示将不同的程序连接为一体。
。其中“о”表示将不同的程序连接为一体。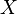 的描述(或者称源代码)写为
的描述(或者称源代码)写为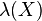 ,则自打印程序的第一条赋值语句就相当于给
,则自打印程序的第一条赋值语句就相当于给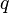 赋予了
赋予了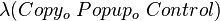 ,即
,即 这三个程序连在一起的源代码。最后我们可以将自打印程序简写为:
这三个程序连在一起的源代码。最后我们可以将自打印程序简写为:S(x){
q= λ (Copyo Popupo Control)
(Copyo Popupo Control)(q); }
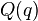 ,其中
,其中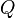 表示(
表示(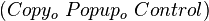 )这三个程序的联合程序,而
)这三个程序的联合程序,而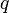 则表示联合程序的源代码。
则表示联合程序的源代码。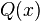 这个程序的作用是输出一个特殊的字符串“
这个程序的作用是输出一个特殊的字符串“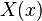 ”即程序
”即程序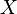 调用自己的代码x的源程序,我们称这个
调用自己的代码x的源程序,我们称这个 为蒯恩函数。
为蒯恩函数。 自己的源代码再喂给它自己,这样就产生了
自己的源代码再喂给它自己,这样就产生了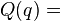 “
“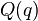 “的效果。等式左边是
“的效果。等式左边是 对
对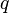 的计算,是一个动作,它的结果产生了等式右边的字符串”
的计算,是一个动作,它的结果产生了等式右边的字符串”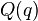 “,而这个字符串恰恰就是
“,而这个字符串恰恰就是 作用于
作用于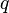 的源代码。我们看到,第2节中的蒯恩方法与这里的
的源代码。我们看到,第2节中的蒯恩方法与这里的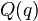 是一模一样的。仔细想想不难发现,其实自打印程序的逻辑与蒯恩语句的逻辑是相通的。因此,自指恰恰就隐藏在了这段自打印程序之中了。
是一模一样的。仔细想想不难发现,其实自打印程序的逻辑与蒯恩语句的逻辑是相通的。因此,自指恰恰就隐藏在了这段自打印程序之中了。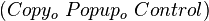 )中的
)中的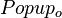 改成Construct就可以了。这里的Construct是一个函数,你输入给Construct一段程序的源代码
改成Construct就可以了。这里的Construct是一个函数,你输入给Construct一段程序的源代码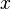 ,它就能把
,它就能把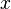 所对应的程序
所对应的程序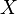 编译出来并驻留在内存中。这样,程序
编译出来并驻留在内存中。这样,程序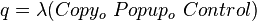 就可以完成自复制功能。
就可以完成自复制功能。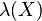 而构造出实际机器
而构造出实际机器 就行了。在冯诺依曼的著作《自复制自动机理论(Theory of Self-reproducing Automata)》一书中,作者试图构建的自复制自动机就包括了这四个部分。即自复制机器是由一个通用拷贝机(Copy)、一个通用构造机(Construct)和一个控制器(Control)以及所有这三台机器的描述即源代码
就行了。在冯诺依曼的著作《自复制自动机理论(Theory of Self-reproducing Automata)》一书中,作者试图构建的自复制自动机就包括了这四个部分。即自复制机器是由一个通用拷贝机(Copy)、一个通用构造机(Construct)和一个控制器(Control)以及所有这三台机器的描述即源代码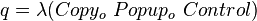 构成的。
构成的。延伸阅读:
论文题目:Large Language Models Can Self-improve
论文链接:https://openreview.net/forum?id=NiEtU7blzN论文题目:Self-Instruct: Aligning Language Model with Self Generated Instructions
论文链接:
https://arxiv.org/abs/2212.10560
大模型2.0读书会启动
o1模型代表大语言模型融合学习与推理的新范式。集智俱乐部联合北京师范大学系统科学学院教授张江、Google DeepMind研究科学家冯熙栋、阿里巴巴强化学习研究员王维埙和中科院信工所张杰共同发起「大模型II:融合学习与推理的大模型新范式 」读书会,本次读书会将关注大模型推理范式的演进、基于搜索与蒙特卡洛树的推理优化、基于强化学习的大模型优化、思维链方法与内化机制、自我改进与推理验证。希望通过读书会探索o1具体实现的技术路径,帮助我们更好的理解机器推理和人工智能的本质。
从2024年11月30日开始,预计每周六进行一次,持续时间预计 6-8 周左右。欢迎感兴趣的朋友报名参加,激发更多的思维火花!
“后ChatGPT”读书会
6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会










