摘要

随机过程边界泛函（如这些过程的极值、首次达到固定水平的时刻、达到该水平时的过程值、达到极值的时刻、过程高于固定水平的时间以及其他泛函）的潜在应用，被用于描述物理、化学和生物问题。给出了这些泛函的定义，并针对具有指数分布的输入需求模型给出了特征函数。还考虑了这些限制的一般化。通过诸如具有亲和力 A 的单环网络、非对称随机游走、非线性扩散、两水平模型、布朗运动以及具有可逆目标结合动力学的多个扩散粒子等示例，展示了边界泛函的潜在用途。

研究领域：随机过程，边界泛函，统计物理，首次通过时间，非线性扩散，风险理论，热力学轨迹

 

论文题目：Application of boundary functionals of random processes in statistical physics
发表时间：2025年2月12日
论文地址：https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.024115
期刊名称：Physical Review E
在统计物理中，随机过程的“边界行为”往往隐藏着关键的系统演化信息。从粒子首次到达某个能级的时间，到生物分子结合靶点的停留时长，这些“越界时刻”的数学描述——边界泛函（boundary functionals）——正成为解码复杂系统动态的新钥匙。近期Physical Review E的一篇研究，系统探讨了边界泛函在物理、化学和生物问题中的应用潜力，为从风险理论到扩散动力学的多领域研究提供了新视角。


什么是边界泛函？

边界泛函是描述随机过程与特定阈值交互行为的数学工具。例如，可用于描述下列情况：
  • 首次通过时间（FPT）：如布朗粒子首次触及某位置的耗时。
  • 极值分布：过程在区间内的最大值/最小值统计特性。
  • 停留时间：系统维持在阈值以上的累计时长，如核反应堆材料在临界温度以上的持续时间。

研究中，作者通过指数分布需求模型构建了这些泛函的特征函数，并推广到更一般的限制条件，为物理系统的风险行为建模奠定了基础。

边界泛函：从金融风险到物理系统

传统上，边界泛函常用于金融风险评估，如保险公司破产概率计算。研究者在本文中将这一数学框架与统计物理结合，提出了两类核心方法：

1. 指数跳跃模型假设随机过程的跳跃幅度服从指数分布，如化学反应中的分子碰撞事件，通过求解Lundberg方程的根ρ±(s)，解析获得FPT、停留时间等泛函的矩生成函数。这种方法成功应用于单循环网络和不对称随机行走的动力学分析。

2. 热力学轨迹映射将边界泛函与轨迹热力学的标度累积生成函数（SCGF）关联，揭示非平衡系统中熵产生与边界行为的定量关系。例如，在二能级模型中，首次通过时间分布可直接关联到系统的熵变速率。

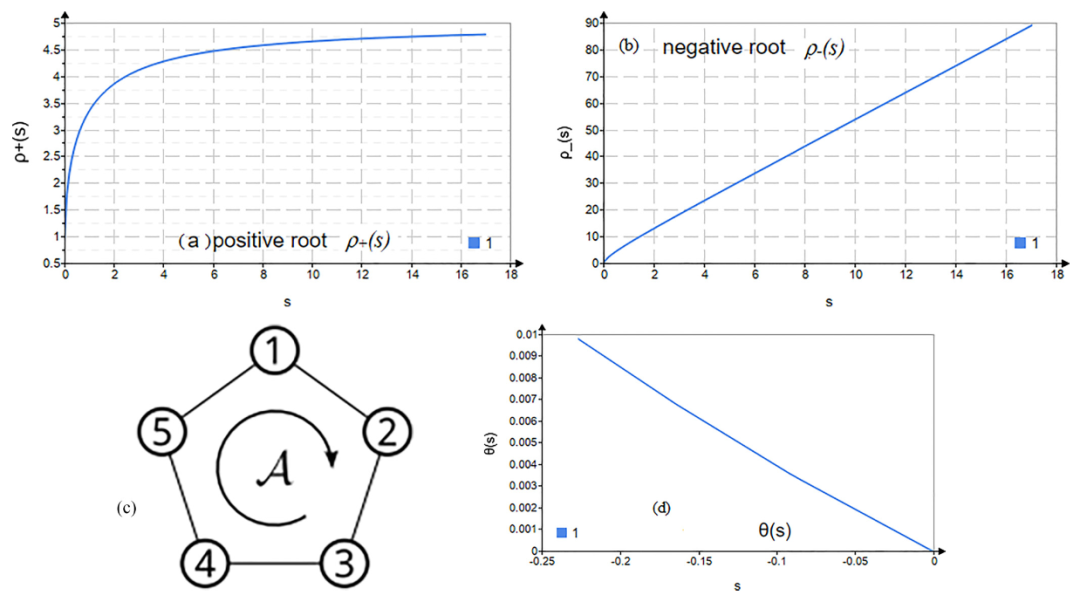
图 1. （a）具有 SCGF 方程（33）的 Lundberg 方程（21）的正根方程（35）。（b）具有 SCGF 方程（33）的 Lundberg 方程（21）的负根方程（35）。（c）具有亲和力 A 和五个状态的单环网络，N = 5。（d）从（b）图中处于活跃相的 s 获得的单位时间动态自由能 θ(s) 的类似物。



物理世界的“越界”案例

1. 非线性扩散中的停留时间当扩散系数随浓度非线性变化时，研究通过随机停止过程（randomly stopped process）量化粒子在阈值以上的驻留概率，其矩生成函数呈现独特的指数衰减形式。

图 2. （a）值 EQx (θs, μ)的行为：对于 s = 10，x = 5 时，取决于参数 μ，红色，约 10−12；对于 s = 1，x = 1 时，取决于参数 μ，黑色，约 10−2。（b）对于 s = 5，μ = 0 时，值 EQx (θs， μ) 对边界值 x 的依赖性。

2.可逆靶标结合动力学在多粒子扩散系统中，如酶与底物结合，结合事件需要至少K个粒子同时到达靶区。通过拉普拉斯变换与风险理论结合，解析预测了“耐心粒子”触发反应的统计规律，为生物传感机制建模提供新工具。

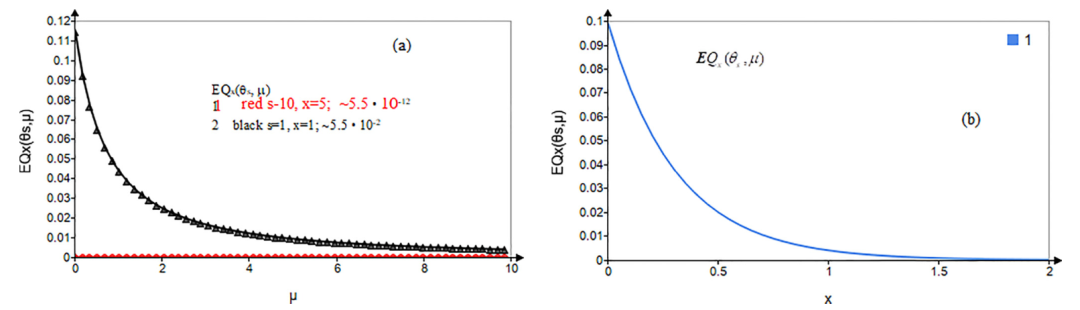
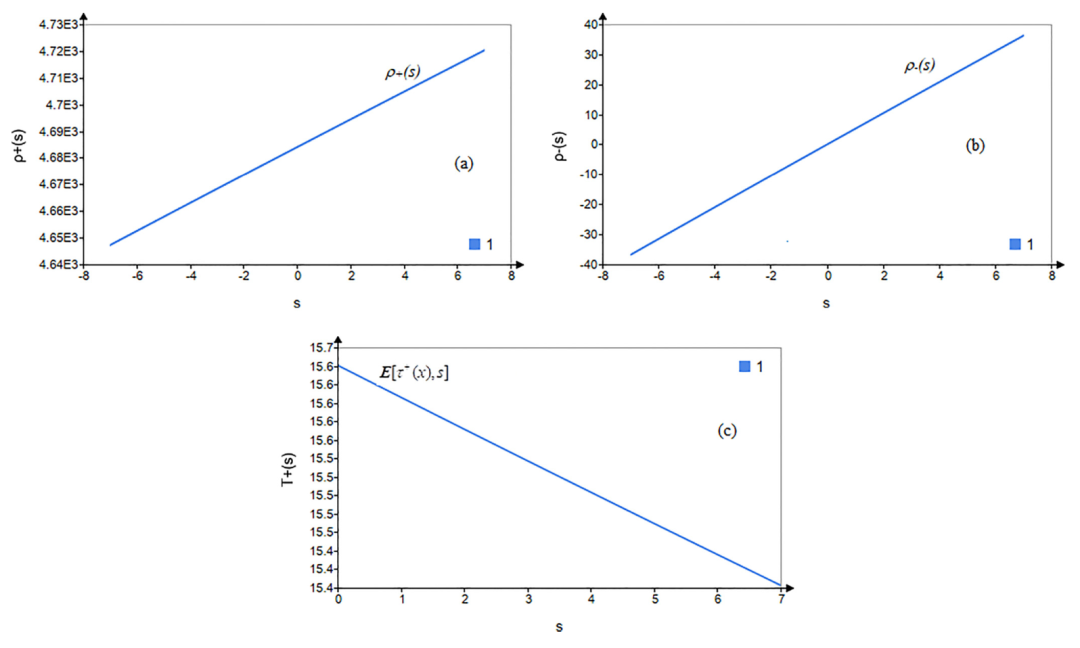
图 3. (a)，(b) 函数ρ±(s)在参数取值为c = 0.2、λ = 0.819、xm = 0.01、x = 3时的行为；(c) 基于式(68)和式(85)计算的，到达阈值x = 3的平均首次通过时间E[τ+(x),s]对参数s的依赖性解析。


3.布朗运动的极值重构对布朗运动ξ(t)=at+σW(t)，其极大值ξ⁺(θₛ)的分布通过Lévy-Khinchin分解显式表达，揭示了随机停止时间θₛ与热力学参数s的深层关联。


为什么这很重要？

这项研究架起了数学概率论与复杂系统物理的桥梁： 将风险理论的物理化，金融中的“破产时刻”概念迁移到物理系统，如材料失效预测；提供了多尺度统一框架：从分子结合到反应堆安全，不同尺度的“越界行为”可用同一类泛函描述；提出非平衡热力学新视角：首次通过时间等泛函可作为热力学力参数，推动非平衡态统计理论发展。 研究者呼吁更多研究关注除FPT外的边界泛函——例如停留时间与极值的联合分布，或许能揭示隐藏在随机涨落中的全新物理规律。当“越界”成为理解复杂系统的关键线索，下一次突破可能就藏在某个随机过程的拐点之中。

彭晨 | 编译

非平衡统计物理读书会启动！

2024年诺贝尔物理学奖授予人工神经网络，这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象，还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来，复杂现象如何涌现。它通过研究大量粒子的集体行为，成功地将微观世界的随机性与宏观世界的确定性联系起来，为我们理解自然界提供了强大的工具，也为机器学习和人工智能领域的发展提供了重要推动力。


为了深入探索统计物理前沿进展，集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元，以及多位国内外知名学者共同发起「非平衡统计物理」读书会。读书会旨在探讨统计物理学的最新理论突破，统计物理在复杂系统和生命科学中的应用，以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始，每周四晚20:00-22:00进行，持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流，一起探索爱因斯坦眼中的普适理论！

图片

详情请见：从热力学、生命到人工智能的统计物理之路：非平衡统计物理读书会启动！

推荐阅读
1. Nature Physics 经典综述：热力学不确定性原理约束非平衡涨落
2. 前沿综述：生物功能的随机热力学
3. Nature Physics 信息热力学经典综述：通往信息的物理本质
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！


点击“阅读原文”，报名读书会