人工智能加速科学仿真、设计、控制和发现
摘要
近年来，随着AI for Science（科学智能）的蓬勃发展，人工智能与各门科学的交叉融合逐渐成为一个显著的科学研究趋势。但是，AI for Science所涉及的范围很广，学科众多，因此，将其梳理成一个统一的体系能够更好地为初入领域的研究者导航。本文认为，尽管各门科学研究的对象、方法看似千差万别，但人工智能可以为科学研究提供一套普适的范式和方法，解决各科学领域内的重要问题。本文将从科学仿真、设计和控制、发现三个方面展开综述，明确任务设置，梳理当前的代表性工作，并通过具体的例子，阐释人工智能如何为科学研究助力，以期使读者能够更好应用已有的方法，或者研究新的方法。
本文发表于《计算物理》，经同意转载。
0. 引言
0. 引言
近年来，人工智能（AI）与科学领域的交叉融合迅猛发展，AI for Science（科学智能）已经成为一个蓬勃发展的交叉学科。尽管各门科学（例如物理、化学、生命科学、材料等）研究的对象、方法看似千差万别，但是 AI for Science 有希望为各门科学提供统一的范式和方法，并极大加速其发展。本文认为，人工智能可以在仿真、设计和控制、发现等三方面，为科学研究提供一套普适的方法，解决领域内重要问题。为此，本文将介绍人工智能用于科学仿真、设计和控制、发现三方面的任务设置和当前进展。在介绍过程中，将着重从一些代表性工作和具体例子出发进行阐释，不求面面俱到，目的是让读者对这一领域有一个初步的认识，从而可以更容易应用已有的方法，或者研究新的方法。
1. AI for Science：从微观到宏观
1. AI for Science：从微观到宏观
图 1 画出了不同学科在时间和空间尺度上所研究的对象的大致范围，从微观的粒子物理、量子计算等，介观的材料科学、细胞生物学等，到宏观的机械、大气、能源、天文学等，我们可以看到，不同学科的研究对象跨越了三十多个空间数量级和二十多个时间数量级。
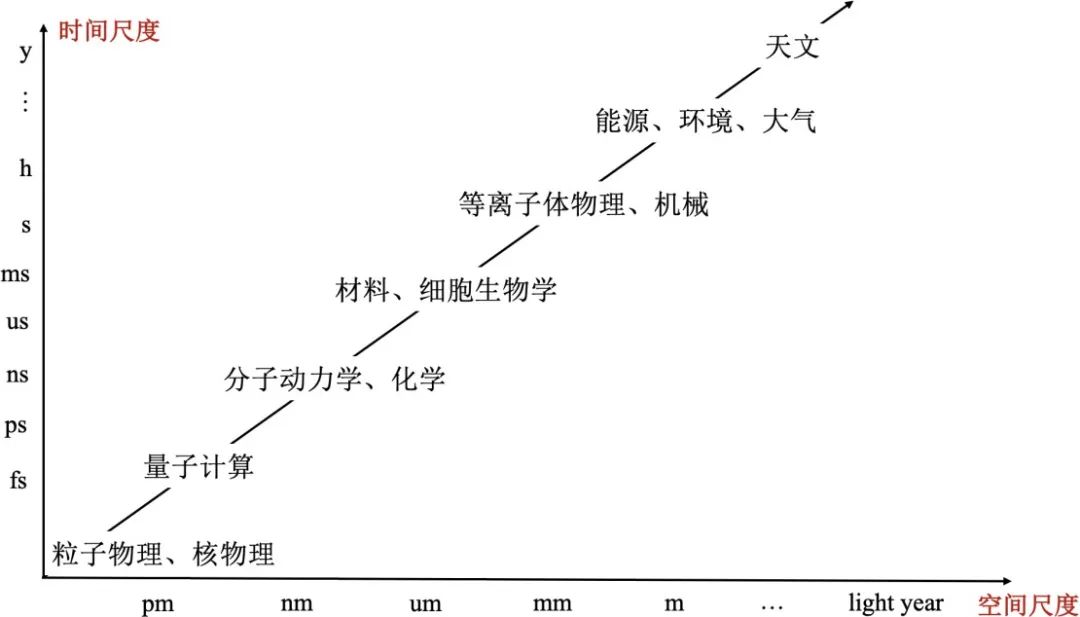
图 1 不同科学领域的大致空间尺度（横轴）和时间尺度（纵轴）
尽管如此，这些不同的学科的研究具有极其显著的共性。具体来说，（1）它们都需要预测所研究系统的状态随时间的演化，或者基于边界条件、结构等预测其稳态和性质，我们称为仿真或模拟。（2）与以上正向问题相反，研究人员通常需要设计系统的参数、结构，逆向优化某些设计目标（逆向设计），或者根据系统当前的稀疏观测推测系统完整的参数和初始条件（逆问题）。同时，研究人员需要控制系统的状态以优化控制目标。（3）此外，研究人员需要从数据以及已有理论出发，发现系统的重要变量和简单普适的方程，构建描述系统的理论和模型，并通过实验验证（科学发现）。以上三类问题，在大多数科学领域中都是普遍存在的核心问题。而人工智能可以为以上问题的解决，带来新的范式和方法，并且成数量级地加速系统的仿真、设计和控制、发现。同时，人工智能结合学科已有的先验知识和方法，可以取得更好的效果。以下三节，将分别进行阐述。
2. 人工智能用于科学仿真
2. 人工智能用于科学仿真
2.1 问题定义和方法分类
仿真，是科学研究中的最重要的普适问题之一。从粒子物理中对粒子衰变的仿真、可控核聚变中等离子体仿真、流体力学仿真，到分子动力学仿真、细胞仿真、天体物理仿真等等，我们都需要根据系统的初始条件和边界条件，模拟一个系统的演化或者预测其稳态。基于此，研究人员可以更好地控制系统的演化，以及优化系统的参数和结构。人工智能用于科学仿真，目的就是提高科学仿真的速度和精度。
首先，我们需要明确系统的描述（图 2）。我们把系统在时间𝑡的状态称为𝑢𝑡，𝑓∗为系统的演化（可能来自真实物理系统的演化，或者求解器）。𝑚𝑡为外界在时间𝑡对系统的控制输入，𝑎为系统的不随时间变化的参数，𝜕𝕏为系统的边界条件。这一描述可以包含大多数系统的演化。
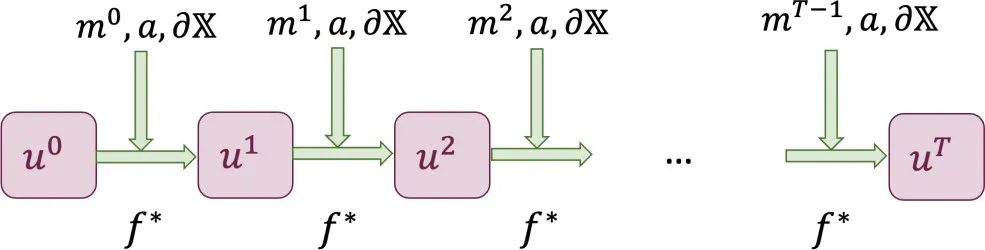
图 2 对于系统动力学的描述设置。
如图 3 所示，根据运用第一性原理和数据驱动的比例，我们可以把不同的仿真方法放在一个光谱上。光谱的最左端是基于第一性原理的传统数值方法，包括分子动力学求解器，有限元、有限差分等偏微分方程数值方法等。光谱的最右端是基于数据驱动的方法。在光谱的中间区域，为两者的有机结合。
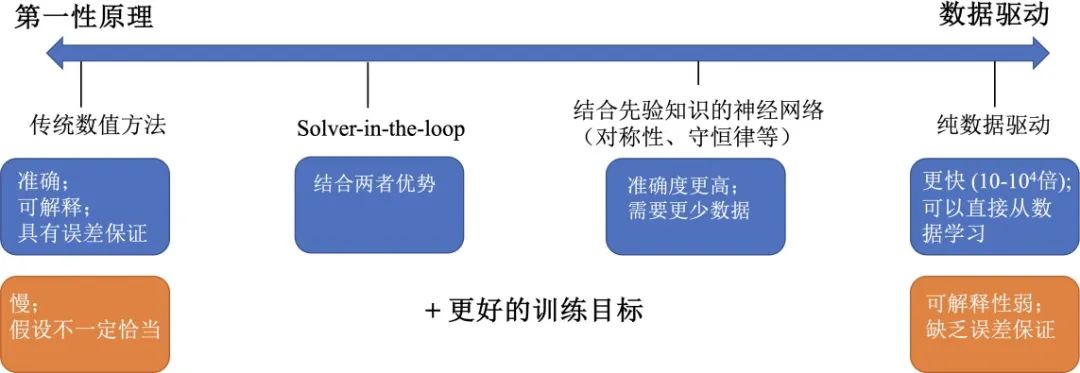
图 3 不同仿真方法在第一性原理的传统数值方法（最左端）到数据驱动（最右端）光谱上的分布，以及其优势（蓝色）和局限性（橙色）。
在光谱的最左端，是基于第一性原理的传统数值方法。例如，对于如下一般的二阶非线性偏微分方程（PDE）：
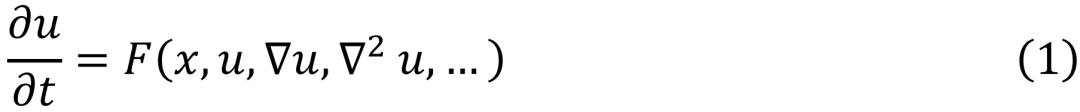
人们通常将其在时间和空间上进行离散化，形成离散的时间状态，以及通过空间上规则或者非规则的网格来表示系统的状态（图 4）。接下来，便可通过有限差分、有限元、有限体积等数值方法进行求解。
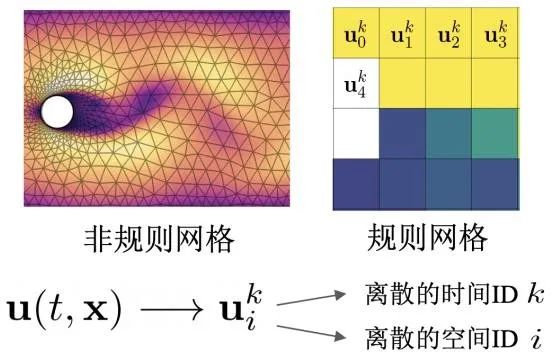
图 4 传统数值方法将偏微分方程在时间和空间上离散化，以便于数值求解。
尽管传统数值方法在准确度、可解释性、误差保证等方面有优势，且经过几 十年的发展，在各领域都建立了各自的求解器，但是，其主要局限性在于求解速度非常慢，往往需要几小时到几天才能模拟一个网格量级千万级以上的大型系统。近几年兴起的基于深度学习的代理模型（简称 AI 仿真模型），能够成数量级地加速以上仿真过程，加速倍数可以达到 10-104 倍。加速的原因在于神经网络可以学习使用更大的时间步长和空间步长，学习效率更高的表示（例如在隐空间进行演化），或者直接学习从初始和边界条件到方程解的映射。此外，如果观测数据量足够，那么 AI 仿真模型可以比传统数值方法更为精确。这是因为传统数值方法基于给定的方程进行离散求解，这些方程往往是真实演化规律的简化或近似；而深度学习直接从观测数据中学习，有望捕捉更为复杂的关系。由此，基于 AI仿真模型为科学仿真带来了新的范式。
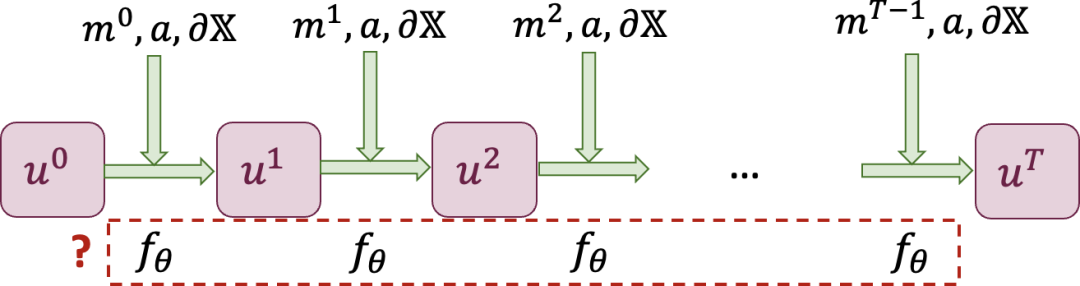
图 5 AI 仿真模型学习一个代理模型𝑓𝜃，最小化预测误差。
具体来说，给定一个包含系统状态轨迹和外界控制序列和参数（但不需要提供方程）的数据集，系统动力学仿真的目标是学习一个 AI 仿真模型模拟系统的演化。通过深度神经网络参数化一个函数𝑓𝜃，这一神经网络根据𝑡时刻的系统状态𝑢𝑡以及参数、边界条件和外界控制来预测下一时刻的系统状态。通过最小化预测状态与𝑡 + 1时刻真实系统状态𝑢𝑡+1之间的误差来进行学习，其优化目标为：
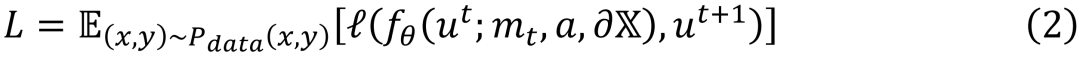
这里𝓁(⋅;⋅)为损失函数，通常为 MSE、MAE 或者其他合适的函数。在推理时，用训练的𝑓𝜃代替求解器，迭代预测系统状态随时间的演化。
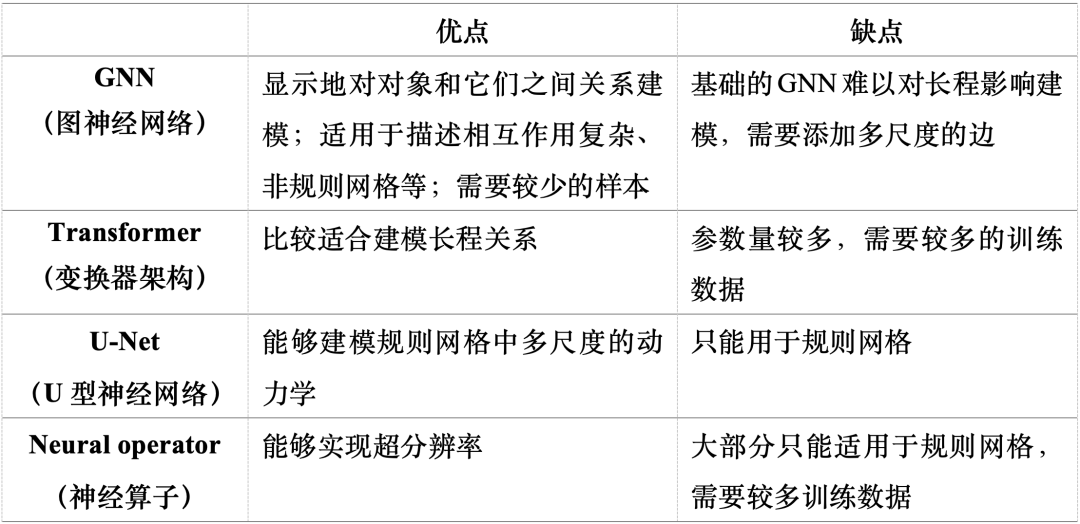
深度学习方法的效果取决于合适的神经网络架构和学习模式。表 1 和表 2 分别列出了 AI 仿真模型常用的神经网络架构和学习范式及其优缺点。这里不同的神经网络架构以及学习范式可以根据需要进行组合。例如，可以将神经算子架构结合物理信息范式[1-2]，这样可以同时利用其超分辨率的优点以及已知的物理方程减小训练数据的需要量。又比如，可以将生成模型与物理信息两个学习范式结合[3]，基于 PDE 和数据生成高维、长程的物理仿真。
表 1：AI 仿真模型常用神经网络架构及其优缺点
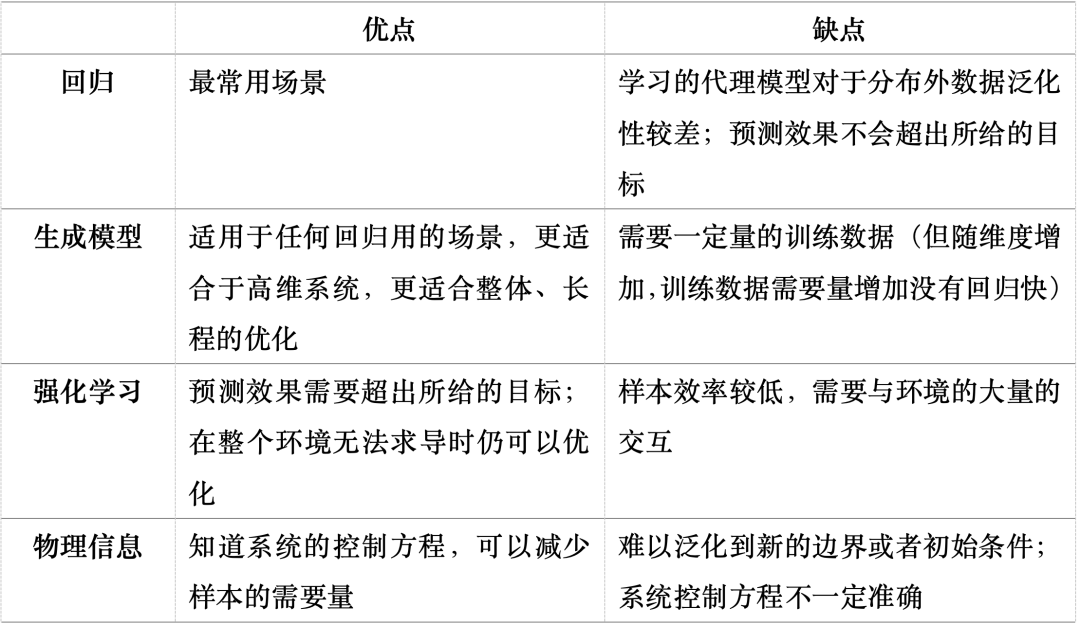
在图 3 光谱的中央，有着一系列结合第一性原理以及数据驱动范式的神经网络架构和学习范式。它们结合两者的优点，适用于已知一部分物理以及有一部分数据（但无大量数据）这一实际中最常见的场景，也是当前 AI+科学仿真的研究前沿。例如，从传统数值方法出发，可以结合神经网络构建 solver-in-the-loop 的范式，通过神经网络学习求解器在低精度网格仿真与真实结果的残差[4-5]，或者根据物理先验构建代理模型的架构[6-7]，从而大大减少训练数据的需要量，提高预测的精确度。另外，从纯数据驱动范式出发，可以在神经网络架构中考虑系统已知的对称性和守恒律，并将其植入到神经网络架构中，使得它们被严格满足。这方面代表性工作有等变图神经网络（EGNN[8]）、深势分子动力学（DPMD[9]）、 Schnet[10]、考虑规范对称性的卷积神经网络[11]，以及[12]提出一套普适方法，可以通过标量或者标量与矢量的乘积，将各连续对称性的等变性或者不变性植入神经网络使其被严格满足。另外，物理信息神经网络（PINN[13]）将方程以及边界条件作为损失加入优化目标，也是一类有效的物理先验植入方法。
2.2 案例研究：图神经网络用于物理系统仿真
在这里，我们以图神经网络（GNN）举例，阐明 AI 仿真模型在具体领域的应用及发展的脉络。首先，2020 年DeepMind 提出Graph Network Simulato（r GNS，图神经网络求解器）架构[14]，将物理系统建模成为粒子系统，通过图神经网络学习粒子之间的相互作用关系，来建模不同的物质（例如流体、沙子、胶泥）的动力学，取得了较好的预测效果（图 6）。
图 6 GNS 将物理系统建模成粒子系统，模拟水流（左）、沙子（中）、胶泥（右）的含时演化。(a) GNS 预测结果；(b) 经过渲染后的结果。图来自[14]。
神经网络架构上，该工作提出 GNS 模型作为代理模型𝑓𝜃，由𝑡时刻系统的状态（所有粒子的位置和速度）预测𝑡 + 1时刻的状态（图 7）。GNS 模型首先通过一个编码器（图 7(c)），将每一个粒子的位置和速度分别映射到一个高维隐空间，并构建图结构。如果两个粒子之间的距离小于设定的阈值，则连接边。边上也可以包含特征，例如相对距离。
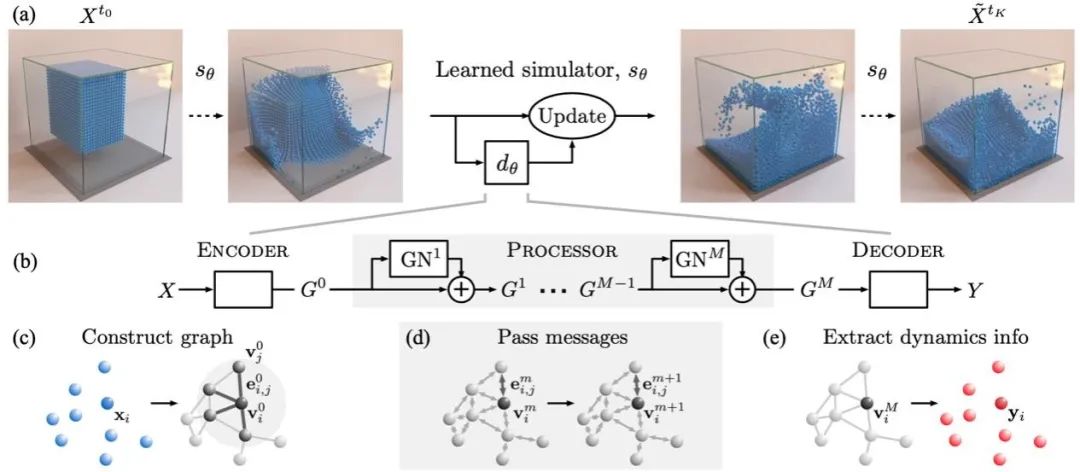
图 7 GNS[14]网络架构。系统在𝑡时刻的状态（各粒子的位置和速度）作为输入，经过(c)编码器, (d)消息传递, (e)解码器，预测𝑡 + 1时刻的加速度，经过欧拉法预测𝑡 + 1时刻的系统状态。
接下来，通过𝑀层的消息传递（message passing），实现图状态的更新。对于每一层的信息传递，包括三步：（1）学习相互作用：首先在每一条边上，根据边的特征和相连的两个节点的特征，通过一个可学习的多层感知机（MLP），预测消息；（2）聚合相互作用：在每个节点上进行消息的聚合，聚合通常采取相加、平均或者取最大值等对于交换不变的操作；（3）学习聚合的相互作用如何影响节点特征：在每个节点上，将聚合的消息与节点当前层的特征进行级联（concatenation），通过另一个可学习的多层感知机，预测节点下一层的特征。
最后，将以上结果输入解码器，预测下一个时间每个节点的状态。在训练时，通过最小化预测误差，反过来学习以上的编码器、解码器和消息传递中的可学习的多层感知机。总而言之，该方法基于实际观测或者仿真数据，通过最小化预测误差，来学习粒子间的相互作用以及相互作用如何改变粒子的状态，本质上是学习了系统的动力学。最后，该工作进行了一系列的实验验证，取得了较好的准确度和效果。
基于该工作，文章[15]提出混合图神经网络（图 8），首次将图神经网络用于百万以上网格的地下流体物理仿真。为了降低长期预测误差，该方法提出训练时最小化多步预测误差（而不是单步预测误差），提高长期预测的精度。同时，由于图神经网络是一个局域模型，其本质上学习的是任何节点如何受到周围节点的作用，因此，该方法只需要十多条系统演化轨迹数据，通过空间的多样性，就可以泛化到全新的初始条件和静态参数。实验表明，该方法相比起传统数值求解器加速 18 倍，相比起之前的深度学习模型，能够更加精确地预测地下流体 20 个月的演化。该方法已经部署于沙特阿美（全球最大石油公司）的仿真管线中，搭配原有求解器，可以实现不同设计和逆问题的快速验证。
图 8 (a) HGNS 架构[15]; (b) HGNS 对水流体积的预测结果（截面）与真实值比较，可见其在20 个月内预测效果与真实值精确符合。
此后，借鉴 HGNS 的多步预测方法，DeepMind 进一步提出 GraphCast 架构 [16]（图 9）用于全球天气预报。这是一个多尺度图神经网络架构，在全球大气的三维网格基础上，添加了六个尺度的粗粒化网格，每个尺度的边跨越距离呈指数增加，并在消息传递时，同时汇聚所有尺度的消息。如此一来，该网络可以学习某一位置的大气的未来状态如何受到临近尺度（几十公里）直到全球尺度（几千公里）大气的影响。由于该方法所学数据来源于实际观测并且数据充足，该方法的精度超过了传统求解器，并且将十天预测的仿真时间由传统求解器的小时量级降到了分钟量级。
除了以上重点介绍的工作之外，基于图神经网络的 AI 仿真涌现出了相当多其他各类重要工作。例如[17]提出 MeshGraphNets（网格图网络），通过非规则网格建模多个刚性或柔性物体，并模拟他们之间的相互作用。[18]提出 LAMP（多分辨率物理仿真）架构用于建模多分辨率物理仿真，通过两个 MeshGraphNets 分别学习系统状态演化和网格的粗化和细化，同时优化预测误差和计算成本。另外，几何图神经网络[6]通过将系统对平移、旋转的等变性融入图神经网络的设计中，可实现对分子性质、动力系统演化的更好预测。
由于能够灵活的建模各类对象的相互作用及影响，图神经网络不仅广泛用于宏观系统偏微分方程的仿真，也运用于粒子物理预测[19]、等离子体物理仿真[20]、凝聚态物理基态求解[21]、材料物理性质预测[22]、分子物理仿真[23]、天体物理仿真[24]等。同时，图神经网络的仿真仍有以下重要开放问题：（1）如何进一步增大图神经网络的表达能力，捕捉更高阶的相互作用；（2）如何将图神经网络拓展到更大规模的仿真问题，进一步提高其效率和精度；（3）如何更好建模多尺度、多物理场问题。以上开放问题值得领域研究者进一步探索，其中（2）（3）也是其他神经网络架构用于科学仿真的开放问题。
2.3 案例研究：神经算子用于仿真和预测
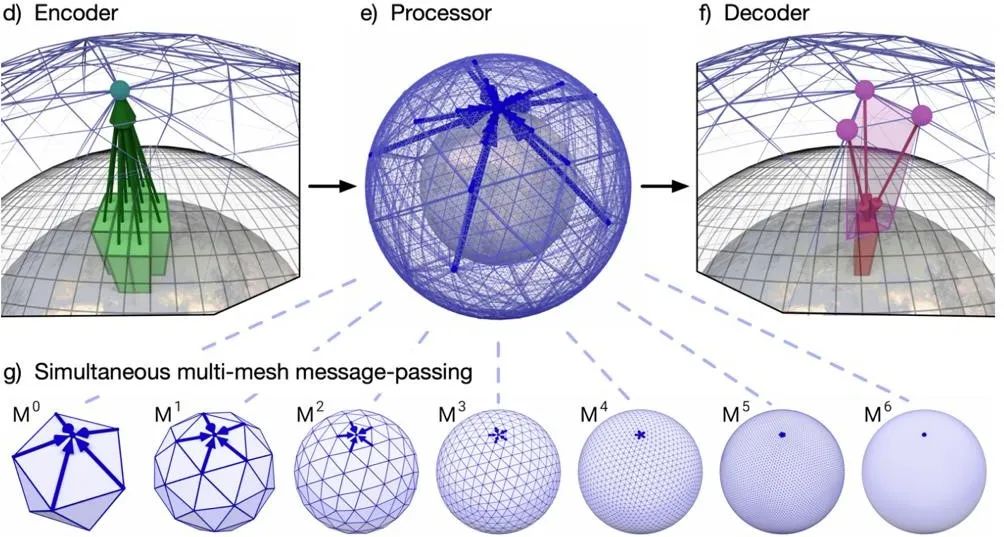
图 9 GraphCast 架构[16]。其构建的多尺度图神经网络，可以同时汇聚局域和多尺度的信息。
除了 2.2 节介绍的图神经网络之外，Transformer、U-Net、神经算子等都是常用的神经网络架构。这里重点介绍神经算子（neural operator）。不同于通常的神经网络将有限维的向量空间映射到有限维的向量空间，神经算子可将无限维的函数映射到另一无限维的函数。因此，其非常适合于偏微分方程的仿真问题。例如，对于边值问题，神经算子𝑓𝜃可以将参数函数𝑎(𝑥)（包含边界）直接映射到方程的解函数𝑢(𝑥)（图 10）。对于初值问题，神经算子可以将初始条件𝑢(𝑡 = 0, 𝑥)映射到整个方程的解𝑢(𝑡, 𝑥)。相比物理信息神经网络（PINN[13]），其不需要对每一个新的参数或者边界条件都重新训练模型，大幅提升了求解速度。
图 10 神经算子可以将无限维的函数映射到另一个无限维函数。
在这里，我们着重介绍傅立叶神经算子（Fourier Neural Operator，FNO）[25]，一类代表性神经算子。傅立叶神经算子（图 11）首先将参数函数𝑎(𝑥)在规则网格上的采样结果映射到一隐空间𝑣0(𝑥)，接下来通过𝑇层的傅立叶层（Fourier layer）实现函数映射，其映射方式包含在原空间的卷积操作，加上一个局域的线性变换，最后经过一个非线性函数𝜎：
𝑣𝑡+1(𝑥) ≔ 𝜎(𝑊𝑣𝑡(𝑥) + (𝒦(𝑎; 𝜙)𝑣𝑡)(𝑥)) (3)
其中，由于原空间的卷积操作对应于频域空间中的相乘操作，因此傅立叶神经算子将卷积操作进一步简化为：
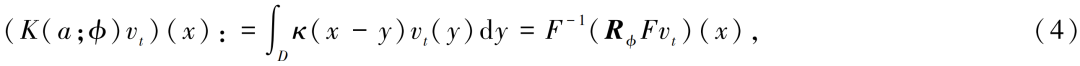
这里𝑅𝜙为可学习的矩阵。通过这种方式，傅立叶神经算子可以同时捕捉全局和局域的信息，并进行高效、准确的预测。
基于基本模型架构，FNO 已经被应用于许多重要的科学领域。例如，文章[26]中提出了 FourCastNet，一个基于深度学习的全球高分辨率天气预报模。其结合了基于傅立叶变换的 token-mixing 和 Vision Transformer (ViT) 骨干网络，傅立叶变化使得模型可以在分辨率无关的方式下学习，而 ViT 骨干网络擅长处理长程依赖。实验表明，它比传统数值模型快 45,000 倍，能够以极低的计算成本生成大规模集成预报，尤其在极端天气事件的预报中表现出色。
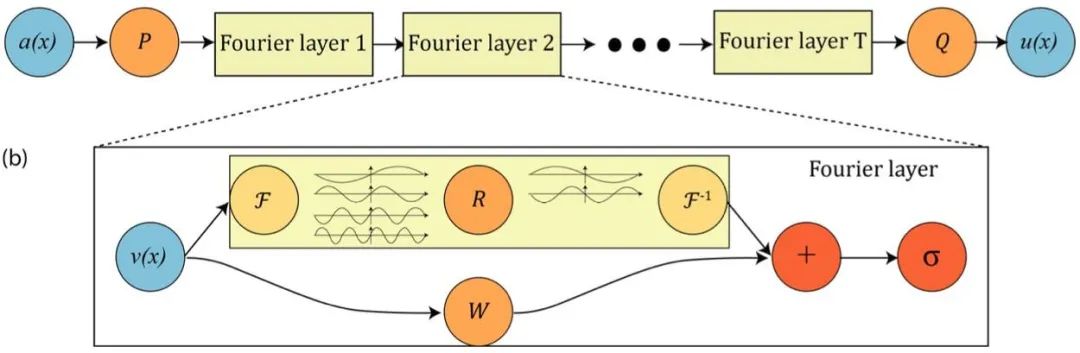
图 11 傅立叶神经算子[26]的网络架构。
除此之外，FNO 也被应用在碳捕集与封存（Carbon Capture and Storage, CCS） 领域中。现有的数值方法在大规模下进行高精度储层压力和气体羽流迁移建模时，计算成本非常高，导致评估存在显著不确定性，进而阻碍了大规模 CCS 的部署。文章[27]中提出了嵌套傅立叶神经算子（Nested FNO），用于在盆地尺度上进行高分辨率的 3D CO2 储存的动态建模。与现有方法相比，Nested FNO 将流动预测速度提升了近 70 万倍，并通过学习偏微分方程组的解算子，为不同储层条件、地质异质性和注入方案提供了通用的数值模拟替代方案，实现了前所未有的实时建模和概率模拟，支持全球 CCS 部署的扩展。
3. 人工智能用于科学设计和控制
3. 人工智能用于科学设计和控制
除了仿真，设计和控制也是各个科学领域的核心、普适问题。对于设计和控制问题，人们通常给定一个目标函数𝐽(𝑢[0,𝑇], 𝑚[0,𝑇])，其为状态轨迹𝑢[0,𝑇]和控制序列𝑚[0,𝑇]的函数。设计和控制的任务设置便是优化初始条件𝑢0，控制序列𝑚[0,𝑇]，
参数𝑎以及边界𝜕𝕏，使得目标函数𝐽最小化，如下图 12 所示。
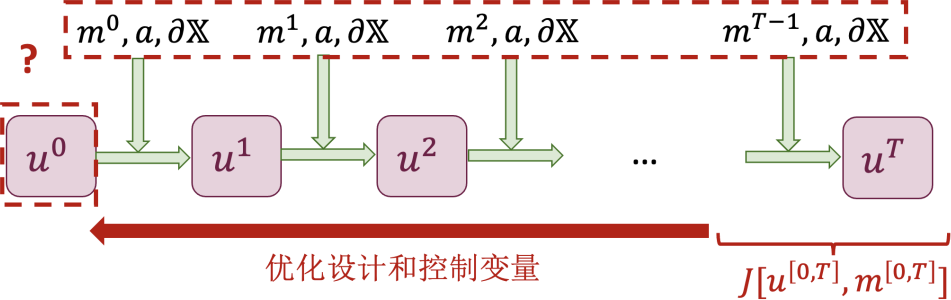
图 12 科学设计和控制的任务设置。根据目标𝐽，优化初始条件𝑢0,控制序列𝑚[0,𝑇]，参数𝑎或者边界𝜕𝕏。
对于不同的待优化变量和优化目标，可以分为以下三类任务：
（1）逆向设计：根据设计目标函数𝐽，优化边界𝜕𝕏、初始条件𝑢0或者参数 𝑎。
（2）逆问题：根据稀疏观测，推测系统的初始条件𝑢0或者参数𝑎，使得模型对系统的预测与观测相符。这里的目标函数𝐽一般为预测误差（例如 MSE）。由于逆问题与逆向设计问题非常相似，我们这里将其归类到设计问题当中。
（3）控制：根据控制目标𝐽，求解接近最优的控制序列𝑚[0,𝑇]。
一般来说，上述设计和控制问题具有很大的挑战性，具体表现为以下三个方面：
（1）高维的设计/控制变量优化空间：对于很多问题，其需要优化的设计变量（例如网格表示的形状、蛋白质序列）或者控制变量（例如软体机器人的形状控制）本身就是高维的，如何在这一高维空间中优化出接近最优的结果具有很大挑战。
（2）复杂的系统动力学：给定设计和控制变量，系统本身的仿真本身可能就非常复杂、耗时（如第 2 节所述），而每一次改变设计和控制变量，传统方法都可能要重新进行一次仿真，因此更加耗时。
（3）泛化到全新设计/控制：对于基于 AI 的设计和控制，往往需要泛化到超出训练集的设计和控制的分布，从而构造出之前没有的新的设计，或者具有更加优越性能的控制序列。这对神经网络的泛化性提出了更高的要求。
对于控制问题，在科学和工程中最常用的是 PID（比例-积分-微分）方法，将当前系统状态与目标状态的差值通过比例、积分和微分运算反馈到对系统的控制输入中，促使系统状态趋向目标。尽管 PID 方法十分容易编程，但调节其系数需要很多的专家经验。同时，对于高维、强耦合的系统，PID 方法难以胜任。对于设计问题，常用的传统方法是将系统的仿真作为内循环，从初始的设计开始，每一次改变设计都需要重新用传统求解器做一次仿真，再根据仿真结果改进系统的设计，因而非常耗时。
由于人工智能的快速发展，近几年涌现出了非常多基于 AI 的设计和控制方法，包括代理模型结合反向传播、深度强化学习、生成模型、PINN、贝叶斯推断、直接映射等。本文将重点介绍前四类方法。
3.1 代理模型结合反向传播方法用于设计和控制
基于第二节所述的 AI 仿真模型，我们可以直接将其用于下游的设计和控制任务。由于 AI 仿真模型是可导（differentiable）的，因此，我们可以用反向传播（backpropagation），将目标𝐽对所需优化的变量（例如边界、参数、控制序列等）求导，以得到更好的设计参数或者控制序列。例如，DeepMind 的工作[28]提出这一方法进行系统边界形状的设计。首先，其通过 MeshGraphNets 来学习系统的仿真代理模型。这一代理模型根据系统的边界形状以及初始条件，预测系统未来的演化。在设计边界的时候，将代理模型的整个仿真轨迹展开，根据给定的设计目标反向传播，以此优化系统边界形状。文章[28]在流体边界形状优化、飞机翼型优化（图 13）等任务中展现了优异的性能，达到或者超过传统求解器（例如 DAFoam）的优化结果，并且效率更高。
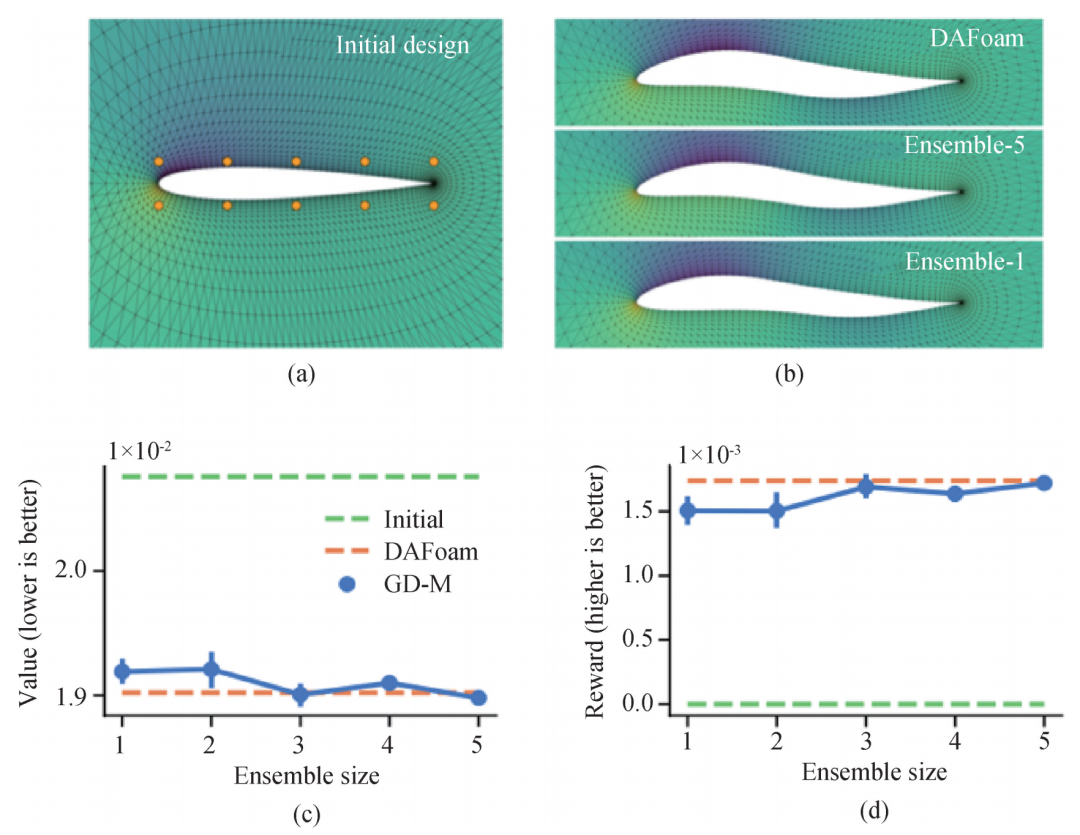
图 13 在工作[28]中对飞机翼型的设计，优化目标为减小阻力。文章提出的基于代理模型+反向传播的方法达到传统求解器（DAFoam）优化的性能，并且速度更快。
这一工作之后，不同工作进行了进一步改进。例如，[29]提出在可学习的隐空间进行仿真和反向传播设计，相对于在原空间进行设计，显著提高了设计的效率。[30]发现，对于逆问题，当需要优化的参数或者初始条件变量维度很高时，直接在原空间进行优化会出现很多具有高频噪声的对抗样本（如图 14 中第一行 without prior 所示）。这是由于在训练时，代理模型只看到了真实系统的演化，而当输入维度很高时，在真实样本的周围，基于神经网络的代理模型会有很多“对抗样本”，其本身并不符合物理，但神经网络仍有可能优化出使得设计目标很好的结果。对于这一问题，[30]提出在隐空间进行优化，由于隐空间的每一个向量都能映射到一个符合先验的初始条件，因此避免了对抗样本的问题。在后文的 3.3节，我们会介绍生成模型方法，也可以解决这个对抗样本的问题。
3.2 深度强化学习用于设计和控制
图 14 文章[30]中实验结果。对于逆问题，如果在原空间进行反向传播优化系统初始条件（第一行，without prior），则会优化出具有高频噪声的对抗样本。而根据文章所提出的在隐空间进行设计，由于有了先验知识，则能优化出与真实值非常一致的初始条件。
除了代理模型结合反向传播的方法，另一类重要的设计和控制方法为深度强化学习。强化学习的设置如下，其包含一个智能体（agent）和环境（environment）的交互（图 15），在每一个时间步，智能体根据当前状态𝑆𝑡，决策下一步行动𝐴𝑡，环境根据当前状态𝑆𝑡和行动𝐴𝑡得到下一步的状态𝑆𝑡+1和给智能体的奖励𝑅𝑡+1。强化学习的目标是学习一个策略函数𝜋(𝐴𝑡|𝑆𝑡)，使得其长期的期望奖励𝔼𝑡[𝑅𝑡]最大化：
当策略函数用深度神经网络参数化时，称为深度强化学习。
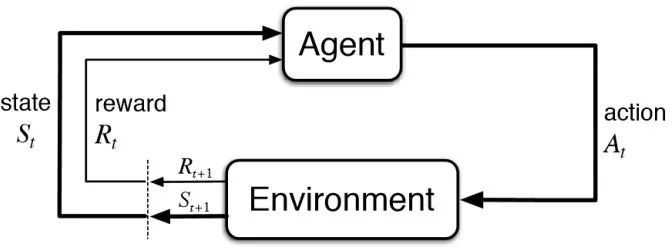
图 15 强化学习设置。
深度强化学习已在各类科学控制任务中得到广泛应用。例如，Degrave 等[16]首次将深度强化学习用于磁约束可控核聚变中托卡马克装置的控制。可控核聚变如果成功，即稳定实现输出能量大于输入能量，那么人类就能获得几乎无尽的免费能源，并可同时解决全球变暖的挑战。磁约束可控核聚变将上千万到上亿度的等离子体通过磁场约束在一个轮胎型的大型托卡马克装置中（图 16），由于温度极高，质量较轻的原子核会碰撞聚变成更重的原子核，同时释放巨大的能量。这一工作的实验任务是根据 92 个传感器的信号，调节 19 个线圈的电流，产生磁场控制信号，使得等离子体能够被囚禁在装置中并稳定放电。由于装置极其复杂，等离子体动力学往往跨越多个尺度，控制频率非常高（10kHz 频率），导致这一控制任务非常困难，传统的 PID 控制方法（图 17f）难以胜任这一任务。
图 16 位于瑞士的 TCV 磁约束可控核聚变托卡马克装置。
基于以上挑战，作者首次提出基于深度强化学习的方法用于托卡马克装置的控制（图 17）。首先，作者在基于传统数值方法的求解器仿真环境中，对强化学习智能体进行训练。其将环境定义为托卡马克装置，系统状态为 92 个传感器的信号，动作空间为 19 个控制线圈的电流，奖励通过等离子体的多个目标参数（包含其位置、形状等）定义。在仿真环境中训练后，作者直接将训练好的模型部署于实际装置中，并进行了一系列实验，表明了该方法的优越性能，包括能够精确控制等离子体的各类参数，以及能够形成新的等离子体位形。这一突破性进展，首次证明了深度强化学习用于控制大型科学设施的可行性，为人工智能在科学控制任务的更多应用揭示了巨大的潜力。
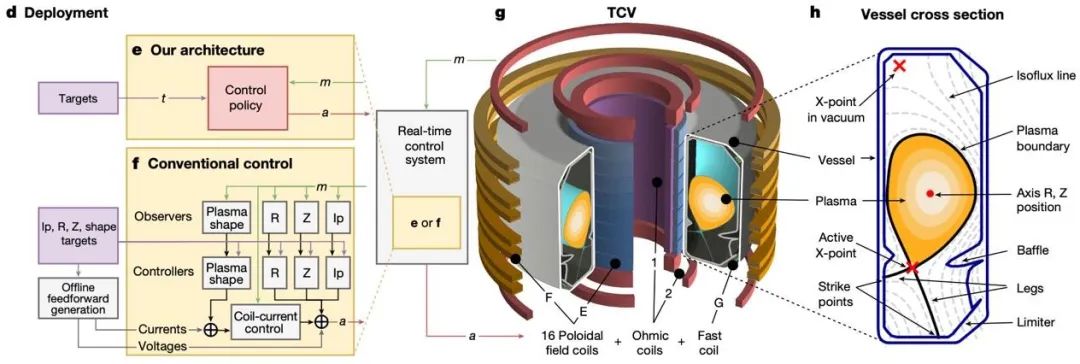
图 17 文章[31]中的深度强化学习与托卡马克装置交互示意图。
除了以上代表性工作，由于其范式的普适性以及优异的效果，深度强化学习已在其他控制和设计任务中广泛应用，例如流体控制[32]、分子设计[33]等等。
3.3 生成模型用于设计和控制
生成模型是一种新的机器学习范式。近几年来，以扩散生成模型为代表，生成模型在图像生成（例如 DALL-E 2）、视频生成（例如 Sora [34]）、3D 模型生成、具身智能等领域涌现出众多令人惊艳的成果。扩散模型对于高维、复杂变量的全局概率建模能力，使其不仅在以上 AI 核心应用领域大放光彩，也使其在科学设计和控制任务中具有巨大潜力。
例如，在工作[35]中，作者针对逆向设计问题，提出基于扩散模型的组合逆向设计方法。其核心在于将仿真和逆向设计融为同一任务，在训练时（图 18 左），
给定系统仿真轨迹𝑢[0,𝑇]和参数𝛾（包含其空间参数、边界等）的数据样本，其可以学习系统仿真轨迹𝑢[0,𝑇]和参数𝛾的联合概率分布𝑝𝜃(𝑢[0,𝑇], 𝛾)，通过参数化的能量函函数𝐸𝜃(𝑢[0,𝑇], 𝛾)表示，其与概率分布的对应关系为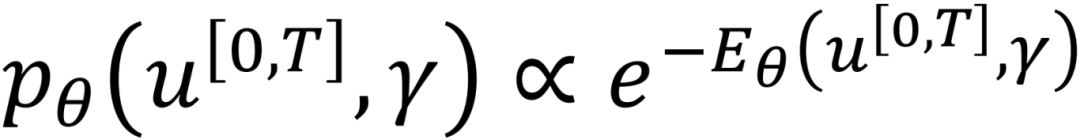
，这个关系表明能量越低，观测概率越高。
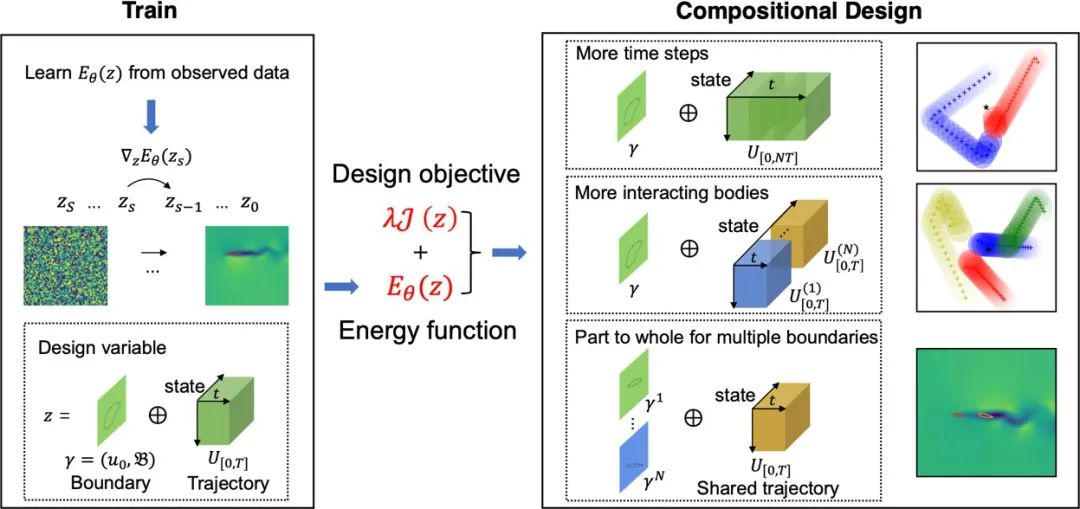
图 18 文章[35]中训练和推理的方法架构。
推理时（图 18 右），该方法将系统仿真轨迹和参数同时生成，并在生成时加上设计目标𝐽(𝑢[0,𝑇], 𝛾)，使得生成的样本既符合物理（即仿真轨迹与参数符合训练集中的联合分布），又能同时优化设计目标。这个同时生成的范式避免了前文 3.1 节方法中每一次改变参数，都需要重新进行仿真的低效做法，同时由于其通过对样本加上噪音再训练去噪网络的方式进行训练，可以有效避免 3.1 中的对抗样本问题。此外，通过能量函数的叠加，该方法能够组合式生成比训练集中更加复杂的参数设计。例如，在飞机翼型设计的实验中，尽管该方法只在训练中见过单个机翼与气流的作用，其在推理中却能同时设计出两个翼型的形状以及相对位置，并发现“编队飞行”的模式能够减小总飞行阻力，实现最大化升阻比的设计目标（图 19）。
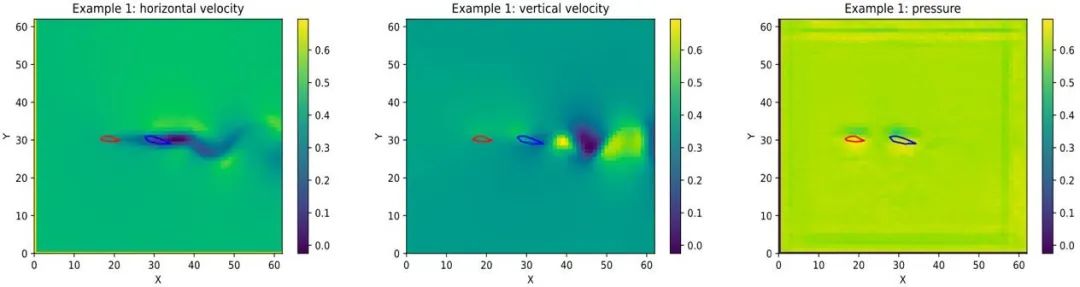
图 19 文章[35]中的方法能同时生成系统仿真轨迹（左：气流水平速度场；中：气流垂直速度场，右：压强场）和机翼形状（中间红色和蓝色形状所示），并发现在训练中未见的“编队飞行”模式。
除此之外，扩散生成模型在其他科学设计和控制任务中也开始广泛应用，例如机械超材料设计[36]，流体控制[37]，蛋白质设计（例如 RFdiffusion[38]，AlphaFold 3[39]）等。基于其在蛋白质设计方面的杰出贡献，David Baker 获得了 2024 年诺贝尔化学奖。其最新的蛋白质设计工作主要基于扩散生成模型。由此可以看到扩散模型等生成模型的潜力，以及广泛应用于各领域的令人兴奋的前景。
3.4 PINN 用于设计和控制
物理信息神经网络（PINN, Physics-Informed Neural Networks）[13]是一种将物理约束与神经网络相结合的数值方法。PINN 通过将 PDE 的具体形式嵌入神经网络的损失函数中，使得网络在学习数据的同时，满足物理定律。它可以用于解决正问题（预测系统的未来状态）和逆问题（根据观测推断系统的未知参数或初始条件），广泛应用于流体动力学、材料科学和气象学等领域。PINN 的优势在于不需要大量数据，也能基于已知的物理模型进行高效的模拟与推断。
给定 PDE 的显式公式，一种自然的想法就是可以利用 PINN，通过同时在损失函数中包含 PDE 和设计、控制目标，可以获得能够最小化目标的设计参数和控制序列。对于逆向设计，考虑到 PINN 中所有约束都是软约束，hPINN 通过使用惩罚法和增广拉格朗日法施加硬约束[40]。之后，为了提高 PINN 的精度和训练效率，gPINN 利用 PDE 残差的梯度信息并将其整合到损失函数中[41]。Bi-PINN[42]进一步提出了一种新颖的双层优化框架，通过解耦目标和约束的优化，避免了无约束问题中细微超参数的设置。另一项研究[43]提出了一种贝叶斯方法，使用数据驱动的基于能量的模型（EBM）作为先验，以提高层析重建的整体准确性和质量。对于利用 PINN 进行控制问题，[44]提出了一种简洁的两阶段方法。首先， 他们通过解决正向问题来训练 PINN 的参数。随后，他们使用一种简单但有效 的线性搜索策略，通过评估控制目标，利用一个单独的 PINN 正向计算将 PINN的最优控制作为输入进行控制。相比之下，控制物理信息神经网络（Control PINNs）[45]是一种单阶段方法，能够同时学习系统状态、伴随系统状态以及最优控制信号。
第一种方法可能计算量大，且由于模型中的间接关系，可能产生非物理结果。至于第二种方法，它可以直接计算变量，并更高效地处理复杂系统，但可能会导致较大的方程组。
3.5 神经算子用于设计和控制
对于偏微分方程（PDE）的一大类逆问题，其定义通常是从算子映射到函数。然而，现有的算子学习框架主要是将函数映射到函数，需要对其进行修改才能从数据中学习逆映射。[46]中提出了一种新的架构，称为神经逆算子（Neural Inverse Operators, NIOs），用于解决这些 PDE 逆问题。受底层数学结构的启发，NIO 基于深度算子网络（DeepONet[47]）和傅立叶神经算子（FNOs）的适当组合，来近似从算子到函数的映射。通过多种实验表明，NIO 在解决 PDE 逆问题时，表现显著优于基线模型，具有鲁棒性和高准确性，并且相比现有的直接方法和 PDE 约束优化方法快了数个数量级。
4. 人工智能用于科学发现
4. 人工智能用于科学发现
科学发现是一个最激动人心的过程，而人工智能正在并且将为科学发现提供一系列强大工具。本文认为，人工智能可以在以下方面，为科学发现助力：（1）发现高维、复杂、强耦合系统中的核心的宏观变量；（2）根据数据，得到变量之间满足的符号方程；（3）发现系统的对称性和守恒量；（4）与人类专家交互，共同证明数学定理；（5）提出实验方案，更好地验证或者证伪当前理论等。
例如，研究者在[48]中提出了 SINDy 算法，其关于模型结构的唯一假设是：只有少数重要的项支配着动力学，因此方程在可能的函数空间中是稀疏的；这一假设在许多物理系统中在适当的基底下成立。具体来说，它使用稀疏回归来确定动态控制方程中所需的最少项，以准确表示数据。这样可以生成既保证准确性又避免模型过度复杂的简约模型，避免过拟合。SINDy 在流体系统上的结果展示了该方法能够发现系统的潜在动力学，该问题花费了领域专家近 30 年才解决。并且，该方法能够推广到参数化的系统、时变的或有外力项的系统。
基于 SINDy 算法，研究者们还提出了许多的变体。比如考虑到现实中观测到的数据会带有噪声，SINDy-PI [49]开发了一种优化和模型选择框架，将隐式的 SINDy 问题重新转换为凸问题，使其具有噪声鲁棒性。[50]基于从噪声测量数据中系统发现问题的弱形式和离散化，提出了提出了 weak-SINDy。这一算法用线性变换和方差缩减技术取代逐点导数近似，能够比标准的 SINDy 算法的精度提高几个数量级。
AI 费曼[51-52]方法（图 20a）也是一个用于发现物理规律的算法，它将分而治之、递归、对称性发现的原理融成统一整体，能够从数据中发现其隐含的复杂方程（图 20b），并且对噪声有较强的鲁棒性。AI 庞加莱方法[53]能够发现物理系统隐含的对称性。例如，其重新发现了著名的古尔斯特兰德-佩恩利夫度量，该度量在非旋转黑洞的史瓦西度量中体现了隐藏的平移对称性。物理学家用了 17 年才发现这一对称性。
图 20 AI 费曼架构(a)及其重新发现的部分方程(b)。
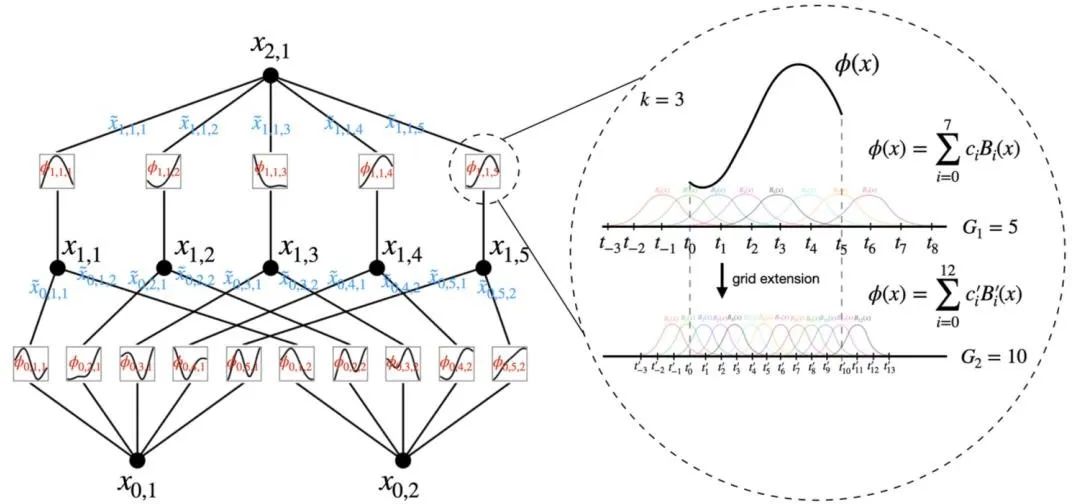
图 21 KAN 架构[54]
另一个最近的代表性工作便是 KAN（柯尔莫哥洛夫-阿诺德网络，图 21）[54]。基于柯尔莫哥洛夫-阿诺德表示定理，KAN 将激活函数放在神经网络的边上，而不是像标准的多层感知机（MLP）把激活函数放在神经网络的节点上。实验表明， KAN 具有很好的可解释性，并能够更快收敛。其在发现系统重要变量、发现神经网络的模块化结构、发现物理系统的方程[55]方面展现了强大的性能以及巨大潜力。
还有的工作提出基于强化学习来进行方程的发现，[56]提出了有限表达法 (finite expression metho, FEX)，它通过强化学习来发现包含有限解析表达式集合的函数空间中的控制方程，其关键概念是通过卷积学习偏微分方程（PDE）解的导数。具体来说，它引入了一种紧凑的操作数树结构，并利用一元运算符，该运算符以具有可训练卷积参数的线性组合的不同操作数作为输入，这一设计有效降低了优化问题的复杂性。
利用遗传算法来进行科学发现也是一个方向，文章[57]中提出了一种符号遗传算法，用于直接从数据中发现开放形式的 PDE（SGA-PDE），并且无需预先了解方程结构。SGA-PDE 使用符号数学来实现任意 PDE 的灵活表示，将 PDE 转换为一个森林，并将每个函数项转换为二叉树；并且采用一种专门设计的遗传算法，通过迭代更新树的拓扑结构和节点属性来有效优化这些二叉树。在实验中， SGA-PDE 不仅成功发现了非线性Burgers 方程、Korteweg-de Vries 方程和Chafee- Infante 方程，还处理了传统的 PDE 发现方法无法解决的有分形结构和复合函数的 PDE。
此外，近年来，许多文章利用大规模语言模型（LLMs）来进行科学发现。通过大语言模型与搜索的交互，[58]提出 FunSearch 方法，其能够生成新的程序来解决数学问题，并在组合数学中得到了新的发现。[59]提出 AlphaGeometry 架构用于几何定理的证明，并在 30 个数学奥林匹克赛题中成功解出 25 道题，接近人类金牌选手的水平。而[60]将 AI 用于化学实验的自动化研究，其将大语言模型作为“中央处理器”，用于调用文档搜索、代码执行和实验自动化等模块，实现化学实验的自动化设计和实施。[61]提出新方法训练 Transformer 以及产生数据集，用于发现动力系统的全局李雅普诺夫函数（Lyapunov functions），以判别系统的稳定性，而这个问题之前没有普适解法。该方法成功发现了一些系统的全局李雅普诺夫函数，超过了传统方法。 [62]讨论了 DiscoveryWorld，一个虚拟环境，用于测试 AI 代理在端到端科学发现中的表现，涵盖了多种挑战，如放射性同位素定年和火箭科学，提供了一个全面的基准来开发科学推理能力。不过，[63]中介绍了 ScienceAgentBench，一个用于评估 LLM 驱动的语言代理在数据驱动科学任务中的基准，其结果突显了当前 LLM 在实现科学研究端到端自动化中的局限性，即使是表现最好的代理在专家支持下也只能独立解决 34%的任务，因此在这个方向还会有很多的进步空间。以上例子只是 AI 在科学发现中的初步应用，其潜力值得广大研究人员的深入探索。
5. 总结
5. 总结
5.1 未来研究方向和开放问题
在人工智能助力科学的仿真、设计和控制领域，让模型更加准确、快速和可信，并能在实际中大规模部署，是一个长期的总体目标。对于仿真领域，目前基于机器学习的方法还难以达到和传统数值方法相近的精度、难以处理复杂的几何结构等等。可能的未来研究方向包括：(1)对于具有多物理场、复杂几何结构、高度非线性或者多尺度特征的系统，开发更好的表示方式和AI仿真方法；(2)开发融合物理先验、仿真数据、实验观测的全新机器学习框架；(3)利用预训练的基础模型 (Foundation Model) 为科学计算多样性场景、数据匮乏的情况下带来优势；(4)开发更加可信的仿真模型，能在全新的环境下预测并给出可证明的误差保证,这对于模型在实际中被大规模采用至关重要。
关于设计与控制，深度学习技术在其上的研究工作相较于仿真还较少。其中一个问题是由与真实物理系统交互的高昂代价，导致的对求解器的需求，甚至是可微的仿真器的需求。此外，如何进行大规模的组合设计，尤其设计出比训练集更加复杂的系统，这在合成生物学、芯片设计、制造业等方面将有广泛应用。此外，另一个重要的研究方向是如何解决现实场景中十分重要的有安全约束的控制问题，使得模型在全新环境下的控制不会超过安全区间。
在人工智能助力科学发现领域，构建一个“AI 科学家”，并真正帮助人类科学家在各门学科实现各类新的发现，是一个令人兴奋的长期总体目标。在这里，[64]提出“AI 笛卡尔”架构（图 22），构想了一个未来的“AI 科学家”可能的组成部分，包括：根据观测数据和先验知识提出新的猜想和理论，通过推理进一步精炼理论，提出实验方案，实际实验验证得到新的观测数据，以上形成一个闭环。我们相信，这样的 AI 科学家将在不久后出现，结合强大的大语言模型作为 “大脑”，并加上人类积累的所有科学知识作为“知识库”，未来将能有效助力各门学科科研的进展。在此之前，这一 AI 科学家的不同部分，包括自动猜想生成、定理自动证明、自动化实验（auto-lab）、科学文献大语言模型等方面将会有突飞猛进的发展。
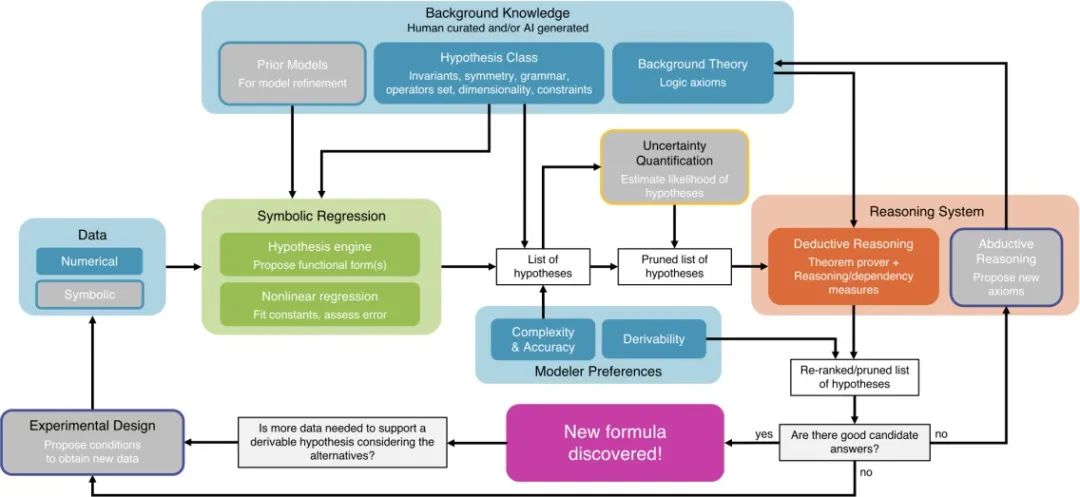
图 22：AI 笛卡尔架构[64]
5.2 总结
人工智能与科学的结合是近几年出现的最激动人心的进展和趋势之一。将人工智能的强大能力渗透到科学研究的各个方面，既能让广大科技工作者拥有一系列强大的工具，加速科研发展；同时，在解决问题的过程中发展出来的新的科学理论和方法，也能反过来推进人工智能的发展。本文从人工智能加速科学仿真、设计和控制、发现三方面，阐述了这些领域的任务设置和一些代表性工作，以期读者能够初步熟悉这些领域。相信随着人工智能与各门科学的进一步交叉、融合，人工智能和科学的发展能够进一步加速，同时会有更多激动人心的发现。
参考文献
[ 1 ] WANG Sifan, WANG Hanwen, PERDIKARIS P. Learning the solution operator of parametric partial differential equations with
physics-informed DeepONets[ J] . Science Advances, 2021, 7(40) : eabi8605.
[ 2 ] LI Zongyi, ZHENG Hongkai, KOVACHKI N, et al. Physics-informed neural operator for learning partial differential equations[ J] . ACM / JMS Journal of Data Science, 2024, 3(1) : 1-27.
[ 3 ] SHU Dule, LI Zijie, BARATI FARIMANI A. A physics-informed diffusion model for high-fidelity flow field reconstruction[ J] . Journal of Computational Physics, 2023, 478: 111972.
[ 4 ] UM K, BRAND R, HOLL P, THUEREY N. Solver-in-the-Loop: Learning from differentiable physics to interact with iterative pde-solvers[C] . Thirty-fourth Annual Conference on Neural Information Processing Systems( NeurIPS) ,Vancouver, Canada,2022.
[ 5 ] PESTOURIE R, MROUEH Y, RACKAUCKAS C. et al. Physics-enhanced deep surrogates for partial differential equations[ J] . Nature Machine Intelligence, 2023, 12(5) : 1458-1465.
[ 6 ] RAO Chengping, REN Pu, WANG Qi, et al. Encoding physics to learn reaction – diffusion processes[ J] . Nature Machine Intelligence, 2023, 5(7) :765-779.
[ 7 ] WANG H, LI J, DWIVEDI A, et al. BENO: Boundary – embedded neural operators for elliptic PDEs [ C] . The Twelfth International Conference on Learning Representations( ICLR) ,Vienna, Austria, 2024.
[ 8 ] SATORRAS V G, HOOGEBOOM E, WELLING M. E ( n ) equivariant graph neural networks [ C ] . The Thirty – eighth International Conference on Machine Learning( ICML) , 2021.
[ 9 ] ZHANG Linfeng, HAN Jiequn, WANG Han, et al. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics[ J] . Physical Review Letters, 2018, 120(14) : 143001.
[10] SCHÜTT K T, KINDERMANS P J, SAUCEDA H E, et al. SchNet: A continuous – filter convolutional neural network for modeling quantum interactions[ C] . The Thirty – first Annual Conference on Neural Information Processing Systems ( NIPS) , Long Beach California USA, 2017.
[11] WEILER M, FORRÉ P, VERLINDE E, et al. Coordinate independent convolutional networks – – isometry and gauge equivariant convolutions on riemannian manifolds [ C ] . The Twelfth International Conference on Learning Representations( ICLR) ,Vienna, Austria, 2024.
[12] VILLAR S, HOGG D W, STOREY-FISHER K, et al. Scalars are universal: Equivariant machine learning, structured like classical physics[C] . The Thirty-fifth Annual Conference on Neural Information Processing Systems(NeurIPS) , 2021.
[13] RAISSI M, PERDIKARI P. KARNIADAKIS G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[ J] . Journal of Computational Physics, 2019, 378: 686-707.
[14] SANCHEZ-GONZALEZ A, GODWIN J, PFAFF T, et al. Learning to simulate complex physics with graph networks[C] . The Thirty-seventh International Conference on Machine Learning( ICML) , 2020.
[15] WU Tailin, WANG Qinchen, ZHANG Yinan, et al. Learning large-scale subsurface simulations with a hybrid graph network simulator[ C] / / Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2020: 4184-4194.
[16] LAM R, SANCHEZ-GONZALEZ A, WILLSON M, et al. Learning skillful medium-range global weather forecasting [ J ] . Science, 2023, 382(6677) : 1416-1421.
[17] PFAFF T, FORTUNATO M, SANCHEZ-GONZALEZ A, et al. Learning mesh-based simulation with graph networks[C] The Ninth International Conference on Learning Representations( ICLR) ,2021.
[18] WU T, MARUYAMA T, ZHAO Q, et al. Learning controllable adaptive simulation for multi – resolution physics [ C] . The Eleventh International Conference on Learning Representations( ICLR) , Kigali, Rwanda,2023.
[19] SHLOMI, J, BATTAGLIA P, VLIMANT J R. Graph neural networks in particle physics[ J] . Machine Learning: Science and Technology, 2020, 2(2) : 021001.
[20] WU Tailin, SUN M, JASON Chou H G, et al. Learning efficient Hybrid particle-continuum Representations of Nonequilibrium N-body systems[EB / OL] . (2023-05-06) . https: / / openreview. net / forum? id = Rd68eTARk4.
[21] LI He, WANG Zun, ZOU Nianlong, et al. Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation[ J] . Nature Computational Science, 2022, 2(6) : 367-377.
[22] XIE T, FU X, GANEA O E, et al. Crystal diffusion variational autoencoder for periodic material generation[ C] . The Tenth International Conference on Learning Representations( ICLR) , 2022.
[23] LI Z, MEIDANI K, YADAV P, FARIMANI A B. Graph neural networks accelerated molecular dynamics[ J] . https: / / arxiv.org / abs/ 2112. 03383, 2022.
[24] VILLANUEVA-DOMINGO P, VILLAESCUSA-NAVARRO V, ANGLÉS-ALCÁZAR, D, et al. Inferring halo masses with graph neural networks[ J] . The Astrophysical Journal, 2022, 935(1) : 30.
[25] LI Z, KOVACHKI N, AZIZZADENESHELI K, et al. Fourier neural operator for parametric partial differential equations[C] . The Ninth International Conference on Learning Representations( ICLR) ,2021.
[26] PATHAK J, SUBRAMANIAN S, HARRINGTON P, et al. FourCastNet: A global data-driven high-resolution weather model using adaptive fourier neural operators[C] . The Eleventh International Conference on Learning Representations( ICLR) ,Kigali, Rwanda,2023.
[27] WEN Gege, LI Zongyi, LONG Qirrui, et al. Real-time high-resolution CO2 geological storage prediction using nested Fourier neural operators[ J] . Energy & Environmental Science, 2023, 16(4) : 1732-1741.
[28] ALLEN K R, LOPEZ-GUEVARA T, STACHENFELD K, et al. Physical design using differentiable learned simulators[ C] .The Twelfth International Conference on Learning Representations( ICLR) , Vienna, Austria,2024.
[29] WU Tailin, MARUYAMA T, LESKOVEC J. Learning to accelerate partial differential equations via latent global evolution
[EB / OL] . Advances in Neural Information Processing Systems, 2022: 10404055(2022-01-01) [ 2024-07-25] . https: / /par. nsf. gov / biblio / 10404055-learning-accelerate-partial-differential-equations-via-latent-global-evolution.
[30] ZHAO Qingqing, LINDELL D, WETZSTEIN G. Learning to solve PDE-constrained inverse problems with graph networks[C] . International Conference on Machine Learning,PMLR,2022.
[31] DEGRAVE J, FELICI F, BUCHLI J, et al. Magnetic control of tokamak plasmas through deep reinforcement learning[ J] .Nature, 2022,602(7897) : 414-419.
[32] RABAULT J, Ren Feng, Zhang Wei, et al. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization[ J] . Journal of Hydrodynamics, 2020, 32: 234-246.
[33] YOU J, LIU B, YING R, et al. Graph convolutional policy network for goal – directed molecular graph generation [ C] . The Thirty-second Annual Conference on Neural Information Processing Systems(NeurIPS) , Montreal, Canada,2018.
[34] OpenAI team. Video generation models as world simulators [ EB / OL] . ( 2024 – 02 – 15) [ 2024 – 07 – 25] . https: / / openai.com / index / video-generation-models-as-world-simulators/ .
[35] WU T, MARUYAMA T, WEI L, et al. Compositional generative inverse design[C] . The Twelfth International Conference on Learning Representations( ICLR) ,Vienna, Austria,2024.
[36] JAN-HENDRIK B, DENNIS M. K. Inverse design of nonlinear mechanical metamaterials via video denoising diffusion models[ J] . Nature Machine Intelligence, 2023, 5(12) : 1466-1475.
[37] WEI L, HU P, FENG R, et al. DiffPhyCon: A generative approach to control complex physical systems[ C] . The Thirty -eighth Annual Conference on Neural Information Processing Systems(NeurIPS) ,New Orleans,2024.
[38] WATSON J L, JUERGENS D, BENNETT N R, et al. De novo design of protein structure and function with RFdiffusion[ J] . Nature, 2023, 620(7976) : 1089-1100.
[39] ABRAMSON JOSH, ADLER JONAS, DUNGER J, et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3[ J] . Nature, 2024, 630: 493-500.
[40] LU Lu, PESTOURIE R, YAO Wenjie, et al. Physics-informed neural networks with hard constraints for inverse design[ J] . SIAM Journal on Scientific Computing, 2021, 43(6) : B1105-B1132.
[41] YU J, LU Lu, MENG Xuhui, et al. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems[ J] . 2022, 393: 114823.
[42] HAO Z, YING C, SU H, et al. Bi-level physics-informed neural networks for PDE constrained optimization using Broyden’s hypergradients[C] . The Eleventh International Conference on Learning Representations( ICLR) ,Kigali, Rwanda, 2023.
[43] POKKUNURU A, ROOSHENAS P, STRAUSS T, et al. Improved training of physics-informed neural networks using energybased priors: A study on electrical impedance tomography[EB / OL] . [ 2024- 07- 30] . https: / / ml4physicalsciences. github.io / 2022 / files/ NeurIPS_ML4PS_2022_92. pdf.
[44] MOWLAVI S, NABI S. Optimal control of PDEs using physics-informed neural networks [ J ] . Journal of Computational Physics, 2023, 473: 111731.
[45] BARRY-STRAUME J, SARSHAR A, POPOV A A, et al. Physics-informed neural networks for PDE-constrained optimization and control[DB / OL] . arXiv, 2022: 03377(2022-08-18) [2024-07-30] . https: / / arxiv. org / abs/ 2205. 03377.
[46] MOLINARO R, YANG Y, ENGQUIST B, et al. Neural inverse operators for solving PDE inverse problems[C] . The Fortieth International Conference on Machine Learning( ICML) ,Honolulu, Hawaii, USA, 2023.
[47] LU Lu, JIN Pengzhan, PANG Guofei, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[ J] . Nature Machine Intelligence, 2021, 3(3) : 218-229.
[48] BRUNTON S L, PROCTOR J L, KUTZ J N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems[ J] . Proceedings of the National Academy of Sciences of the United States of America, 2016, 113( 15) :3932-3937.
[49] KAHEMAN K, KUTZ J N, BRUNTON S L. SINDy-PI: a robust algorithm for parallel implicit sparse identification of nonlinear dynamics[ J] . Proceedings. Mathematical, Physical, and Engineering Sciences, 2020, 476(2242) : 20200279.
[50] MESSENGER D A, BORTZ D M. WEAK SINDy: GALERKIN-BASED DATA-DRIVEN MODEL SELECTION[ J] . Multiscale Modeling & Simulation, 2021, 19(3) : 1474-1497.
[51] UDRESCU S M, TEGMARK M. AI feynman: a physics-inspired method for symbolic regression [ J] . Science Advances,2020, 6(16) : eaay2631.
[52] UDRESCU S M, TAN A, FENG J, et al. AI Feynman 2. 0: Pareto-optimal symbolic regression exploiting graph modularity
[C] . Thirty-Fourth Annual Conference on Neural Information Processing Systems(NeurIPS) ,Vancouver, Canada,2020.
[53] LIU Ziming, TEGMARK M. Machine learning hidden symmetries[ J] . Physical Review Letters, 2022, 128(18) : 180201.
[54] LIU Ziming, WANG Yixuan, VAIDYA S, et al. KAN: Kolmogorov-Arnold Networks[DB / OL] . arXiv, 2024: 19756(2024-04-30) [2024-07-30] . https: / / arxiv. org / abs/ 2404. 19756.
[55] LIU Ziming, MA Pingchuan, WANG Yixuan, et al. KAN 2. 0: Kolmogorov-arnold networks meet science[ DB / OL] . arXiv, 2024: 10205(2024-08-19) [2024-07-30] . https: / / arxiv. org / html / 2408. 10205v1.
[56] JIANG Z, WANG C, YANG H. Finite expression methods for discovering physical laws from data [ C ] . The Twelfth International Conference on Learning Representations( ICLR) ,Vienna, Austria, 2024.
[57] CHEN Yuntian, LUO Yingtao, LIU Qiang, et al. Symbolic genetic algorithm for discovering open-form partial differential equations( SGA-PDE) [ J] . Physical Review Research, 2022, 4(2) : 023174.
[58] ROMERA-PAREDES R B, BAREKATAIN M, NOVIKOV A, et al. Mathematical discoveries from program search with large language models[ J] . Nature, 2024, 625(7995) : 468-475.
[59] TRINH T H, WU Yuhuai, LE Q V, et al. Solving olympiad geometry without human demonstrations[ J] . Nature, 2024, 625:476-482.
[60] BOIKO D A, MACKNIGHT R, Kline B, et al. Autonomous chemical research with large language models[ J] . Nature, 2023,624(7992) : 570-578.
[61] ALFARANO A, CHARTON F, HAYAT A, et al. Global Lyapunov functions: a long-standing open problem in mathematics,with symbolic transformersp[C] . The Twelfth International Conference on Learning Representations( ICLR) ,Vienna, Austria,2024.
[62] JANSEN P, CÔTÉ M A, KHOT T, et al. DiscoveryWorld: A virtual environment for developing and evaluating automated scientific discovery agents[ C] . The Thirty-eighth Annual Conference on Neural Information Processing Systems( NeurIPS) ,New Orleans,2024.
[63] MAJUMDER B P, TAFJORD O, CLARK P. ScienceAgentBench: Toward rigorous assessment of language agents for data-driven scientific discovery[ C] . The Twelfth International Conference on Learning Representations( ICLR) , Vienna, Austria,2024.
[64] CORNELIO C, DASH S, AUSTEL V, et al. Combining data and theory for derivable scientific discovery with AI-Descartes[ J] . Nature Communications, 2023, 14(1) : 1777.
参考文献可上下滑动查看
-直播预告-
非平衡统计物理读书会启动！
2024年诺贝尔物理学奖授予人工神经网络，这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象，还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来，复杂现象如何涌现。它通过研究大量粒子的集体行为，成功地将微观世界的随机性与宏观世界的确定性联系起来，为我们理解自然界提供了强大的工具，也为机器学习和人工智能领域的发展提供了重要推动力。
为了深入探索统计物理前沿进展，集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元，以及多位国内外知名学者共同发起「非平衡统计物理」读书会。读书会旨在探讨统计物理学的最新理论突破，统计物理在复杂系统和生命科学中的应用，以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始，每周四晚20:00-22:00进行，持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流，一起探索爱因斯坦眼中的普适理论！
详情请见：从热力学、生命到人工智能的统计物理之路：非平衡统计物理读书会启动！
6. 探索者计划 | 集智俱乐部2025内容团队招募（全职&兼职）
微信扫一扫,分享到朋友圈
