摘要


重整化群 (renormalization group, RG)理论是一套强有力的理论框架，主要应用于多自由度系统的研究。该理论通过对系统状态、模型参数和耦合常数在不同尺度下的描述，实现系统在不同分辨率层次间的转换。该理论不仅能识别相变临界点，还能有效分析系统在临界点附近的行为特征。在传统物理应用中，重整化群理论通常基于同质性 (homogeneity)、对称性、几何结构和局部性 (locality) 等基础概念，构建度量距离、尺度变换和自相似粗粒化方案。近年来，研究者们致力于将该理论拓展至复杂网络研究。然而，复杂网络系统普遍存在三个显著特征：显式几何坐标的缺失、节点与子图统计性质的异质性，以及类均匀格点的对称性的缺乏，这些特性导致建立统一的重整化流程面临严峻挑战。本文系统梳理网络重整化领域的主流研究方法，评述重要理论突破，并着重探讨当前尚未解决的关键科学问题。


关键词：重整化群，复杂网络，网络粗粒化，几何重整化，拉普拉斯重整化，多尺度网络

图片

Andrea Gabrielli, Diego Garlaschelli, Subodh P. Patil, M. Ángeles Serrano丨作者

诸葛昌靖丨译者

陶如意丨审校




讲座推荐

关于重整化群，你绝对不能错过的一次分享👇



论文题目：Network renormalization

论文地址：https://www.nature.com/articles/s42254-025-00817-5

论文来源：Nature review physics



本文要点

  • 重整化群的方法已经证明在理解和分类具有多自由度的物理系统的整体行为中具有广泛的不可或缺性；

  • 直接应用传统物理系统的重整化群技术对于复杂网络来说存在困难，这源于度量距离、几何规律性或拓扑规则性等内蕴性质的缺失；

  • 尽管存在这些挑战，重整化群的应用在若干场景中仍取得了显著进展，本技术综述将系统梳理这些成果；

  • 诸多开放性问题依然存在，该论文基于第一性原理，总结更具普适性的网络重整化框架构建的理论依据，尝试阐明其实现路径。




目录

  • 引言

  • 复杂网络重整化的挑战

  • 网络粗粒化方法

    • 基于最短路的方法

    • 谱方法

    • 拓扑方法

    • 对称方法

    • 工程技术和计算机科学中的粗粒化

    • 信息论方法

    • 重整化群方法的基本原理

  • 几何网络重整化

    • 几何模型

    • 几何重整化技术

    • 推广到带权网络

    • 自相似细粒化

    • 应用

  • 拉普拉斯网络重整化

    • 将拉普拉斯扩散视为近邻检测

    • 实空间中的拉普拉斯重整化群

    • k-空间上的拉普拉斯重整化群

    • 扩散演化算子的统计物理学解释

    • 拓扑标度不变网络

  • 多尺度网络的重整化

    • 节点聚合下的不变性

    • 带独立边的多尺度模型

    • 参数重整化与聚合不变性

    • 真实世界网络重整化的淬火变形

    • 集群无标度网络与细粒度化的退火变形

  • 展望

    • 分辨率水平

    • 与动力学过程相容重整化

    • 广义临界性？

    • 信息论视角下的参数相关性与无关性

    • 信息几何与参数流






引言




重整化和可重整化是现代物理学理解宇宙中物质现象的基础概念，该理论假定在足够大的时空尺度上，小尺度细节是可以被平均掉的，从而解释了为什么我们在日常生活中无需了解亚原子粒子水平的精确行为。重整化方法的形式化花费了物理学家数十年时间，并最终促成了对某些物理现象普遍性的惊人洞察。知识框1 总结了传统应用于物理系统的重整化和重整化群变换的基本概念。

除了“传统”物理系统，自然界和社会中的大型复杂系统也包含多个相互作用的尺度，且没有先验的最佳分辨率尺度。因而自然会问，在这些情况下，重整化是否同样适用？例如，在建模企业间商品和服务流动时，当将企业聚集成更广泛的类别（如经济部门）时，其关系是否能被一致地表示？同样，在考虑网络上的流行病传播时，人们希望探索当模型和参数具有不确定性时，基于聚合的分析结果在长期行为上是否与仓室模型的结果有所不同。

尽管将物理系统的研究经验直接移植到复杂网络上可能很诱人，但必须批判性地重新审视其中的关键假设，包括在物质通常具备的相互作用的局部性和空间规则性——其中无序性通常可视为小扰动。此外，在考虑网络上的动态过程时，必须确保无论是对于特定个体还是对统计系综，任何粗粒化方法能够都能搞保持原先的动力学性质。因此，有必要重新审视重整化的基本前提，即通过对小尺度的平均来理解整体的行为，并且在复杂系统的意义下重新表述重整化方法也十分重要。

本文将系统综述重整化方法在复杂网络中的应用，分析真实世界的网络的典型特征：普遍缺乏显式几何结构嵌入、多尺度异质性和不同尺度间的交互连接，并揭示在这些特性要求下，需要如何对传统重整化方法进行根本性改造。本文首先回顾了基于多种粗粒化方案实现的网络重整化方法，继而考查从不同理论基础出发、旨在将重整化群核心原理推广至含异质性与无序性网络的研究路径，最终厘清该领域中尚未解决的开放问题和待探索方向。



知识框1 | 统计物理和场论中的重整化


物理系统中相互作用的局部性与因果性协同作用会限制小尺度涨落的影响，使得宏观尺度下仅需少量参数即可刻画该系统。该思想的规范化始于20世纪60年代，Leo Kadanoff将粗粒化概念（早期由Paul与Tatiana Ehrenfest[167]研究）应用于统计力学系统，以理解其二阶相变临界点邻域的行为[118]。


Ising模型是经典范例，其晶格自旋经历无序态与有序态（磁化态）之间的相变。通过引入“块自旋”自由度可实现模型的粗粒化。块自旋变量间相互作用的标度行为通过重整化群理论[111]得以形式化。早期基于晶格的数值计算[168]之后发展为更普适的变分方法[169–172]。


重整化群理论通过在实空间可用的方法对微观细节进行形式化平均，从而定义了任意尺度下的有效自由度与相互作用，成为统计力学的重大突破。Kenneth Wilson后续将其发展为连续场论中的重整化方法[113,173]。Wilson的工作不仅为理解临界现象的标度行为奠定理论基础，更将场论中处理名义发散量的零散方法系统化。这些发散性源于数学上为解决任意小尺度问题的理想化操作，虽然研究者们对此曾提出减除方案[174]，但该方案在重整化群理论建立前缺乏概念基础。此后，重整化群方法催生了“理论之理论”，揭示微观细节迥异的物理系统在临界点附近如何出现普适行为[175–179]。


过去五十年间，重整化群技术已扩展至从最大尺度的宇宙学到最小尺度的粒子物理等广泛领域。在统计力学范畴内，重整化群方法已推广至同质均匀的分形格点上的非平衡系统[180–186]，其局部平移不变性能够简化计算。超越初始应用的重要范例包括：流行病动力学模型[187]、生物群体行为动力学[188–190]、神经网络[191–194]、动态与有向逾渗[195,196]、观点动力学的选民模型[197]，以及一维链[198]、格点[199]和层级树[200]上非线性振子模型（如Kuramoto模型[120,121]）的同步模型。此外，重整化群方法在张量网络[192,201–203]及信息论框架[204–208]中亦获成功应用。


与平衡态不同，非平衡系统中决定普适类的要素往往未知，且微扰处理中高阶重整化群计算通常不可行。非微扰重整化群作为有潜力的替代方案[209–212]，已应用于格点上的流行病扩散动力学模型等研究[213]。






复杂网络重整化的挑战




应用重整化群方法，研究者们已成功发现了一大类系统的普适性特征，对构建自然现象的自下而上的模型具有重要价值。然而在更多真实世界问题中，相互作用极少呈现类格点似的同质规则性。结构无序性与空间非均匀相互作用导致了具有拓扑几何异质性的网络模式（pattern）。真实世界网络的特征包括：第一，度分布（节点连接数的分布）具有多样性；第二，即使是大规模网络，其任意两点间的平均路径长度往往也很短（即小世界网络特性）；第三，即使是稀疏网络，其局部三角密度（集聚系数）也是非零的有限值；第四，模块化的社区结构或层级型结构等[1-4]。这些不规则特征对推广标准重整化群方法构成挑战，同时系统有限性引起的边界效应与有限尺度的效应[5-9]会导致问题更加复杂。

利用重整化群对系统进行分析，通常由以下三个基本步骤组成。第一，定义粗粒化变量。可以是在实空间中将粗粒化变量定义为包含多个微观单元的相同介观单元或者定义为能够平铺实空间“模块”；也可以将其定义为在对偶的 k-空间中将变量分解为从最短到最长的不同波长的分量；第二，利用求平均或边缘分布，约化掉系统中由局部涨落为代表的微小细节，即将小尺度单元或短波长（快速）模态等属性进行平均化，从而得到更上一层级的性质；第三，对粗粒化系统的耦合模式和参数数值进行重整化。（在具有连续自由度的理论中，重整化还需要一些技巧来处理不可避免出现的无穷大。这种方法在粒子物理学和统计场论中是熟知的[10,11]，但在当前复杂网络的背景下，由于离散和有限性质，不需要这种额外的处理手段）。这些操作的重复执行，可以产生重整化流（RG flow），其轨迹和不动点也是研究对象之一。

第一步是定义粗粒化变量。这对于嵌入在平移不变的度量空间（如规则格点或欧几里得几何）中的具有局部相互作用的均匀物理系统来说是直接的，因为距离和邻域的概念使得“相同的介观单元”或“波长”易于定义（例如，二维格子可以容易地粗粒化到一个具有相同对称性和维度的缩小格子上）。在具有全局均匀同质相互作用的系统中，如在平均场模型中理想化的那样，系统的结构是可以简单地映射到一个全连接的图上。然而，在高度非均匀和小世界网络中定义粗粒化变量变得不那么简单，这提出了一个问题：在这个背景下，如何适当地定义块节点或慢模态？ 此外，这类网络通常是使用经验信息的分辨率水平构建的，这些水平通常受到数据限制的约束。例如，流行病传播和经济冲击通常是在聚合水平上观察到的（比如亚群体的接触或经济部门流动），而不是在实际动态发生的更细尺度上（个体感染或公司层面的传播冲击）。直接在这些聚合水平上建模过程通常无法捕捉到系统在更细尺度上的动态，这一点在2008年金融危机期间的冲击传播研究和COVID-19爆发期间的流行病传播研究中有所体现[12,13]。

第二步是平均掉局部波动。与第一步类似类似，在同质格点或度量空间中，利用内部对称性，可以通过坐标化定义的邻近性刻画连通性概念，即空间上更接近的节点更有可能连接。在这些空间上的物理理论是局部的，粗粒化理论只涉及局部场及其有限阶导数。然而，局部性概念并不能直接推广到不规则的网络化空间的情形。在对称的布尔网络中，可以通过邻接矩阵（刻画相邻直接相互作用）或其幂（刻画直到第n级近邻的相互作用）来定义相互作用，也可以使用最短路诱导的离散度量[14]。网络的稀疏性、不同路径距离处度分布的异质分布以及无序长程相互作用（小世界特性）等诸多因素使得在复杂网络中明确定义局部性变得复杂。

最后，第三步是重整化耦合和参数。这一步的复杂性与前两步密切相关。在无序的格点系统（如自旋玻璃[15]）中，相互作用拓扑可能是规则的，但耦合常数的异质可能非常高。这种异质性可以用随机变量建模，其中自平均能确保空间平均对应于分布平均。在这种情况下，重整化耦合需要将细尺度耦合常数的概率分布对应到粗粒化后的常数的诱导分布上[16]。在异质网络中，挑战更加严峻，因为相互作用的拓扑本身是无规则的。由于许多复杂网络是基于特定性质从系综中抽样而得到的随机图，因此，重整化耦合模式和参数数值需要将细粒度图上的初始概率分布变换到粗粒度图上的新分布。从理论上来说，该变换定义了一个重整化流，具有其自身独特的泛函轨迹和不动点。

受这些考虑的启发，近年来研究人员致力于为复杂网络重整化建立通用框架。下文将总结各不同但相互关联的一系列策略来实现这一目标的方法。我们首先对粗粒化复杂网络的方法进行宽泛（但依然无法全面的）概述，然后深入探讨在异质网络上述对重整化程序的三个步骤中的若干步骤进行推广的方法。




网络粗粒化方法




由于真实世界中的复杂网络普遍缺乏基本格点结构，因此建立统一的粗粒化方案变得十分复杂，这同时也催生了若干大类的多样化方法。

基于最短路的方法

采用最短路的长度定义节点间距是网络粗粒化方法之一，该方法借助分形几何中的盒覆盖思想（box-covering）[17,18]实现迭代重整化群变换。该方法以最短路距离为度规（注：数学上通常称为度量），将指定距离内的节点聚合成粗粒化节点形成更粗的空间分辨率，从而生成重整化群序列[14]。此方法能够揭示网络的自相似性与分形特征[14,19–21]，并能给出新生长机制[22]和网络普适类分类[5,23]。然而受限于小世界特性，以最短路为距离准则的重整化群变换难以有效解耦和揭示标度行为。因此，这类变换下度分布的自相似性并不伴随关联函数的标度律而出现，特别是在网络集聚方面，这个特征表现得更加明显。

另一方面，研究者提出，可以在具有短程连接性质的规则格点网络中添加长程连接，进而实现实空间重整化群变换。这类变换已用于研究若干问题，包括Watts-Strogatz模型在临界点附近的行为（在最短路密度趋于零的极限情形[24]）以及经变换其拓扑性质保持不变的格点上的无标度网络模型[25]。然而，这些方法需预知节点坐标，或需明确区分短程连接（定义实际参与粗粒化的路径长度）与长程连接。对于真实网络，这类信息通常未知甚至无法明确定义。

谱方法

另一种方法基于网络的谱性质，该类方法通过保持特定过程的动力学行为的方式进行粗粒化处理。谱粗粒化方法最初是为研究网络上的随机游走而设计的，其通过保留随机矩阵的最大特征值及对应特征向量来确保大尺度行为的保持，在有效剔除快模态的同时保持慢模态不变[26]。该方法已推广至二部网络（bipartite networks）[27]，并已用于耦合振子的同步动力学研究中，此时网络的拉普拉斯矩阵成为这一方法的核心算符（注：“算符”在数学上通常称为“算子”）[28–30]。类似的谱粗粒化思想也可以用于有向网络的同步[31]和可控性分析[32]等研究。使用图的拉普拉斯矩阵的特征向量与特征值，研究者进一步利用确定性多层网络（如高斯模型的Cayley树和钻石晶格[33,34]）探索了场论重整化群方法对处理有序-无序现象的可能性[33]。这些研究为建立基于拉普拉斯谱的图重整化理论框架[35]奠定了基础，本文后续将对此设立独立章节进行详细讨论。

拓扑方法

与上述方法并行发展的，是基于拓扑性质的粗粒化方法。这类技术包括：节点中心性度量（如度[36]和广义度[37]）、基于邻居重叠的节点相似性度量[38]，这包括传统的社交网络中的结构等效节点[39]、食物网中的营养等效物种[40]的概念等）、以及作为反复重现的模式的网络模体分析[41]等。

特别值得关注的方法还包括诸如基于度阈值的重整化[42]和k核分解[43]等节点剔除方法。前者通过移除度低于特定阈值的节点来定义嵌套子图的层级结构；后者将网络分解为一系列极大子图，并确保子图的每个顶点均满足最小度约束。这些方法在真实系统中有效揭示了超越度分布标度不变性的层级自相似性，例如聚类谱（clustering spectrum）的标度律。

此外，研究者还提出了基于多尺度社区检测中模块化概念的策略[44]，其思路类似于计算机科学中的多层图划分算法。这类算法包含基于节点或边属性的粗粒化启发式方法，例如针对连接均匀分布的图的重边启发式算法，通过合并具有大权值连接的节点实现粗粒化[45]。对于具有度分布呈幂律的图，也可以使用基于社区的粗粒化方案，将高度互连的顶点集合并[46]。

拓扑方法依赖于特定结构模式，例如层级社区结构或结构等价节点的存在，因而当这些特征缺失时，该方法会失效。这个局限性具有物理学中典型的重整化相矛盾的风险，这是因为后者要求即使缺乏介观特征，仍能对简单晶格系统进行一致且可迭代的粗粒化操作。

对称方法

另一种针对过程的方法利用对称性定义的等价类来构造粗粒化方案。在从生物科学到计算机科学的研究中，能够表征网络上动态过程局部对称性的方法为刻画系统基本模块提供了普适性原则[47]。具体而言，当网络在节点变换下能够保持输入树不变（input trees invariant）时，网络会涌现均衡划分（equitable partitions）[48]，该性质已被用于定义常微分方程的成块性（lumpability）[49,50]、布尔后向等价（Boolean backward equivalence）[51]以及纤维染色性质（fibration colouring）[52]等概念。

对称性诱导的均衡划分可将系统约化为保留整体动力学与同步特性的动力学变量的集合，此特性充分证明了该方法的实用性[53]。尽管基于对称性的方法识别针对过程的等价类节点这一重要网络约化技术极为有效，但其通常仅能确定单一划分（通常对应最大网络约化）。与纯拓扑学方法类似，这类方法无法迭代应用（注：无法迭代是因为经过一步约化后，对称性或拓扑性质就发生了改变。），且在对称性缺失的体系中缺乏普适性。

工程技术和计算机科学中的粗粒化

开发互联网及其他通信与交通网络的缩尺工程模型方法，一直是通信技术领域研究的长期目标[54–56]。近年来，如何在保持图结构关键属性基本不变的前提下缩减其规模，也成为机器学习领域的重要课题——图嵌入技术和图神经网络等深度学习工具正日益广泛应用于图结构数据分析。粗粒化方案旨在通过压缩图结构降低实际应用中的计算成本与复杂度[57–63]，其在设计高效通信与数据存储纠错编码方面具有重要价值。研究者已运用重整化群方法生成小型网络编码，可有效计算树状网络中置信传播的性能[64]。尽管这些方法受网络重整化思想驱动，但其通常聚焦于特定过程，对图结构数据与复杂系统多尺度本质的底层原理揭示有限。

关于关于文献63的论文解读

海报预览

信息论方法

信息论方法也能够探索网络不同尺度间的相互作用。在复杂网络中，更大尺度通常能提供关于网络连接结构的更丰富的信息量，这一现象称为因果涌现现象[65]，因果涌现可有效降低节点间关系观测的不确定性。此外，针对具有特定的图上的动力学过程，可能存在多种捕捉原始过程不同特征的粗粒化描述。信息论方法有助于评估网络动力学过程状态空间的划分如何影响其约化后的动力学行为[66]。

重整化群方法的基本原理

真实世界网络的异质性可能使得不同方法得到的结果出现相互矛盾，解决这种方法上的不等价性需要基于第一性原理建立适用范围更广泛的复杂网络重整化框架。构建这样的框架需要重新审视重整化方案的根基，也就是，那些相对成熟的，定义在具备规则格点和均匀同质度量的系统上的重整化方法，同时也需注意前述章节讨论的挑战。接下来，我们将回顾应对这些挑战而尝试的不同方法。为了便于讨论，我们首先为读者们讲解其中的一些共同基础。

我们首先讨论粗粒化变量的定义。为了固定符号，引入  的邻接矩阵  来表示在给定分辨率尺度下的网络，即对给定的层级（尺度）  ，  代表该在层级能够观察到的节点数。  表示“最精细”层级（即网络数据可用的原始层级），而  表示粗粒化过程的第  次迭代（在考虑“细粒化”方法时，也允许“负层级”  的出现，稍后会进一步解释）。对于加权网络，还需要用于表示链接强度的权重矩阵  。

对变量的粗粒化可以通过不同方式实现。推广“实空间”重整化程序的方法通过“块节点”来定义粗粒化变量，这些块节点决定了下一层级邻接矩阵的行和列。对于这些方法，定义“空间平铺”（tiling）的等价操作是定义特定的划分  ，满足将第  层级的  个节点  映射到下一层级  的数量更少的  个粗粒化节点（“块”）  。而那些试图推广 k 空间重整化程序的方法则是需要去给出推广的“对偶空间”的定义，这可以通过将格点分解为基本模态的邻接矩阵的显式算符表示来实现。（注：一个线性空间的对偶空间在数学上粗略地是指这个线性空间上的所有线性泛函所构成的线性空间。）

对实空间中精细细节的积分消去操作（“积掉”），其本质是定义了一个  到  的满射（即多对一映射，因而是不可逆的），同时如果需要，还需定义从  到  的满射，而在k空间中则需要定义对偶算子在相邻层级间的类似映射。对此的自然选择是采用局部映射，即粗粒化矩阵  的元素  和  仅依赖于细粒度矩阵中包含于该粗粒化节点的微观节点的元  ，即

其中  表示某个函数。例如，在纯二值层级上，当且仅当在  层级上存在从块  “内部”任意节点（记为  ）到块  “内部”任意节点（类似地记为  ）的至少一条连边时，块  到块  的连边才存在。此粗粒化步骤生成的邻接矩阵  的元素可以表示为：

类似地，可以引入一个局部方案，从  获得粗粒化矩阵  ：

其中  表示一个函数。需要注意的是，  和  的选择的自由度导致了结果对方案的依赖性，这是任何重整化群方法中都普遍存在的需要注意的事项。更重要的是，如上所述，  和  是满射，因此一般不可逆：这些性质对应于小尺度信息丢失，使得重整化群仅能成为半群。类似地，对偶空间方法中对快模态有损积分也具有相同的性质。

最后，需要将重整化推广到耦合系数和模型参数上。如果网络是一个单一的确定性图（例如经验网络），具有某些特定的互作模式或过程特征，那么这最后一步取决于耦合系数和模型参数本身的性质。对于过程与该网络在其对偶空间中的表示能够一一对应，那么这一步骤可以直接从积分掉小尺度细节的步骤的结果中得出，例如，在拉普拉斯网络重整化部分中详细讨论的扩散过程。相反，如果“网络”不是确定性的，而是由随机图模型（带有其自身参数）表示，也就是说，网络在原始分辨率  时已经具有多次统计抽样，那么重整化耦合还需要包括随机图参数的重整化，例如几何网络重整化和多尺度网络重整化部分所讨论的内容。这样做需要对图和随机图模型参数上诱导概率分布的函数流进行单独分析。需要强调的是，在其不动点处（概率分布不再改变其形状，而仅改变其参数），重整化流可能会在统计上“可逆”，即可以通过参数变化将概率分布的流从较高层级逆向到较低层级。如果将其应用在原始层级  上，这种逆向的流实际上可能产生网络的细粒化版本（  ），会具有更多的节点，并且通常具有更稀疏的拓扑结构。

完成了上述的梳理之后，本文将介绍三种不同的方法，以互补的方式解决引言中讨论的三个步骤。




几何网络重整化




复杂网络中的空间局部性可通过几何框架恢复[67]，该框架通过将真实网络嵌入双曲空间，将结构异质性与非局部性转化为局部性特征，从而恢复几何重整化群方法[68–71]的适用性。

几何模型

几何软配置模型[42,72]基于节点间的流行度（popularity）与相似性（similarity）来定义节点间的度量距离。这些抽象维度的结合使得双曲几何成为可嵌入层级结构与小世界结构的最自然的空间。此空间中的距离编码了节点间形成连接的概率，邻近节点更倾向于连接。该方法与随机几何图[73,74]及社交网络隐空间模型[75]的思路相似。

在该模型的牛顿版本[42]（称为  模型）中，第  层的每个节点  （  ）被赋予一个流行度变量及相似性空间中的坐标。流行度由隐藏度  编码，该隐藏度从任意分布  中抽取，通常为指数  的幂律分布（  ）。当维度  时，相似性空间为半径为  的一维球面，其设计需满足  个节点以恒定密度分布，其中每个节点  被赋予角坐标  ，由此定义节点对  与  之间的角距离  。节点  与  的连接概率  遵循引力定律形式[76]，并定义了最大熵[2]系综

其中

参数  决定了平均度  ，且各节点的期望度与其  值成正比。  调控网络拓扑的集聚性，反映隐空间中的三角不等式约束，并作为逆温度参数[76,77]。

该模型在  处呈现反常拓扑相变（参考文献77）。在几何相（  ）中，集聚系数保持有限值[42]；而在非几何相（  ）的热力学极限下，集聚系数趋于零。然而，在准几何区域  内，集聚系数衰减至零的速度极慢[78]，表明有限规模网络仍保留显著水平的集聚性，能够与某些真实复杂网络具有相当性质。因此，较低“温度”（低  ）对应短程连接占优，而较高“温度”（高  ）则是对不同长度连接的生成概率的平衡。

 模型具有纯几何形式——  模型[72]，其中隐藏度  对应于径向坐标  ，从而将连接概率（方程(4)）转换为仅依赖于双曲空间中节点间距的费米-狄拉克函数。Mercator工具[79,80]通过统计推断与机器学习技术，最大化观测网络结构与  （等价于  ）模型[81]的契合度，将真实网络嵌入此空间。生成的空间映射可进一步用于可视化、分析、导航及重整化等下游任务。

该模型族能有效解释真实网络连接性的关键特征，包括异质度分布[42,72,82]、显著集聚性[42,72,82–84]、小世界现象[42,85–87]、渗流性质[88–90]、谱特征[91]及自相似性[42]。该框架还可以进一步扩展至生长网络的优先连接机制[92]、加权网络[93]、二部网络[94,95]、互补性驱动网络[96]、多层网络[97,98]、具有社区结构的网络[99–101]、有向网络[102]以及节点含关联特征的网络[103]。


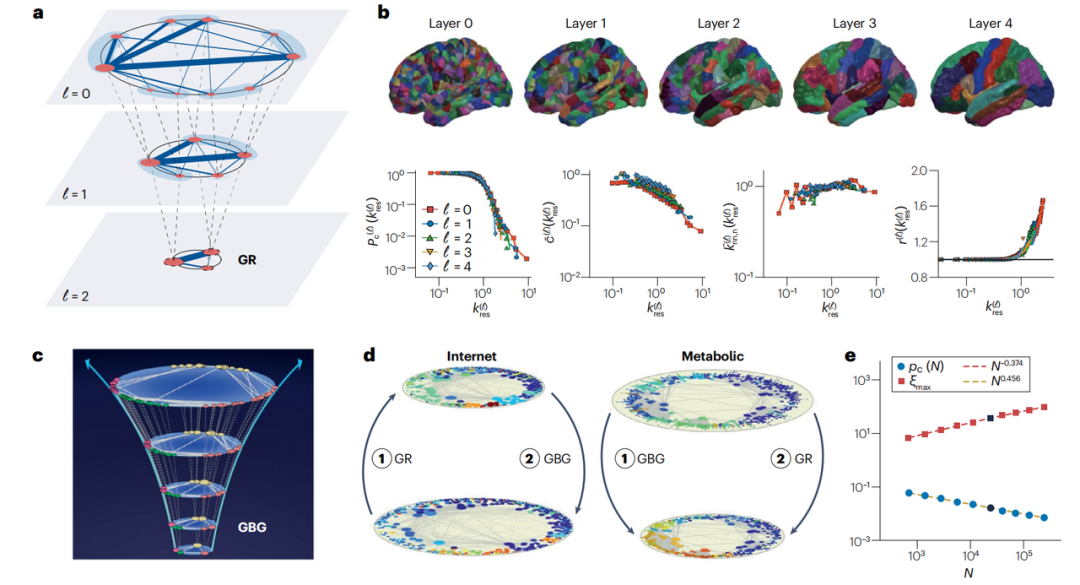
图1  真实网络上几何重整化的直接与逆向方法及其结果。 a. 几何重整化（GR）变换示意图。在层级  中，沿相似性圆定义  个连续节点组成的非重叠蓝色块，从而将原  个节点划分为  个块，形成分区  。这些块被粗粒化为层级  中的超节点，每个超节点的角坐标由其  层构成节点所在区域确定。如方程(2)所述连接  层的超节点，该过程可迭代生成  层。由于半群性质，  层亦可直接通过  的块从  层生成。b. GR 复现人脑连接组的多尺度连通结构。基于解剖数据重建五级长度尺度的多尺度层级表示（上图）。各尺度  下连接组的拓扑特性（符号）与基于最高分辨率几何映射的 GR 预测（曲线）高度吻合（下图）。从左至右依次为：互补累积度分布  、聚类系数  、归一化最近邻平均度  及富俱乐部系数  。计算中采用重整化度  以消除各层级平均度差异的影响。 c. 几何分支生长过程（GBG）以自相似方式演化网络。d. GBG 是 GR 的统计逆过程：对互联网重整化层级应用 GBG 可恢复原始网络的统计等效结构；反之，对 GBG 生成的人体代谢网络替代体应用 GR 可复原原始架构。e. GR 与 GBG 的结合为单实例真实网络的有限尺寸标度研究提供方法，可数值估算临界指数。以互联网链路随机失效的键逾渗模拟为例，网络尺寸  、临界键占据概率  及磁化率最大值  均符合幂律关系（黑色符号为原始网络数据）。GBG 与 GR 壳层参数为分支率  、块尺寸  ，结果表明互联网图存在逾渗阈值消失现象，符合无标度网络预期。图a改编自文献[70]（Springer Nature Limited）；图b转载自文献[104]（PNAS）；图c、d、e改编自文献[69]（PNAS）。

几何重整化技术

 或  模型通过对网络的双曲映射进行迭代操作，从而为复杂网络的几何重整化群奠定了基础[68-71]。在  层中配置好嵌入空间中的坐标后，通过粗粒化和重标度得到新的一层  。这涉及通过分区  将相似性子空间划分为  个扇区（即重整化三步曲中的第一步），使同一扇区  （  ）内的节点  成为超节点。如果原始节点之间至少存在一个连接，如公式 (2) 所示（图1a），则超节点之间建立连边，从而平均掉更尺度更小的细节。迭代此过程，通过逐步选择更长程的连接，生成跨尺度  的重整化流。

几何重整化表明，多尺度自相似性可以作为真实世界的网络中跨领域普遍存在的对称性[68,71]，并且还能准确预测人类大脑连接组的多尺度重构中观察到的自相似性，这些发现表明几何重整化非常接近于小世界和非小世界机制之间的临界结构转变[104]（图1b）。这些发现可由  或  模型在几何（  ）[68] 和非几何（  ）[71] 机制下的可重整化性所解释。对隐藏度的尺度变换是通过要求连接概率不变性（公式 (4)）的条件下获得的。角度坐标流式可由任何保持原始模型旋转不变性的变换来定义。记  ，则保持连接概率并因而在重整化流中能够保持网络拓扑性质的变换可写为

其中，约定  表示属于超节点  的节点。上述变换重整化了耦合系数和参数值。

全局参数的演化如下：  ，  ，其中  是等大小超节点中的节点数，  是尺度不变的。这些变换满足半群性质：用  个节点的组重整化两次等同于用  个节点的组重整化一次。概率  保持  的原始形式，当  时（参考文献 68），平均度  是具有流  的观测量。只要具备良好的嵌入，上述行为性质也适用于真实网络。真实网络通畅具备典型特征  ， 表明流会趋向于高连接度的图；而如果  ，网络的流会趋向于一维环；在小世界和非小世界阶段之间的转变处，  ，平均度保持不变（更多细节见原文附录）。最后，对于  ，链接数在重整化下保持不变[71]。

推广到带权网络

通过保持权重与度关系的变换，网络的权重结构在重整化群流中可以得以保留。几何权重重整化（geometric renormalization of weights，GRW）技术[70]由此产生，它可以对加权网络结构进行多尺度展开[105,106]，从而形成自相似层级。该技术的数学基础在于加权  模型的可重整化性[93]。在实际操作中，通常选择重整化链接的最大权重作为近似方法。在包括细胞中的代谢网络、商业机场之间的航班网络、科学合作网络等来自不同领域的异质度分布加权网络中，使用这种称为sup-GRW的策略或基于其理论的变换[70]进行粗粒化和重标度时，均可以观察到几何标度行为（详见附录）。

自相似细粒化

几何分支生长（geometric branching growth，GBG）模型[69]作为几何重整化的逆向技术，能准确预测真实世界的增长网络的自相似行为，例如世界贸易网和期刊引文网络的长期演化行为。该模型通过生成自相似度量推广来复制网络原始结构，可推广至任意大网络规模。

为了从层级  开始生成几何分支生长模型细粒度层级  （相对于粗粒化方向的“反向”），将原始层级中的节点以概率  划分为  个后代（图1c），从而使节点数量增加为  ，其中  为分支率。不分裂的节点保留其坐标，每个后代节点赋予新的坐标。后代的隐藏度必须通过满足公式 (6) 来遵循几何重整化规则，并且它们的分布  也应保持与祖先层级的分布相同，这就要求度分布必须是一个稳定分布[107]。此外，它们的角坐标固定在祖先的左右两侧，可以略有角偏移，以保持其旋转顺序。更多细节见附录。一旦为后代分配了坐标，就需要确定新层级中的连接，以确保生成的网络属于  系综。

设  ，迭代应用几何分支生长模型将生成一系列逐渐细粒化的自相似层级，也就是说，原始的经验连接概率、度分布、集聚系数和社区结构在流中得以保留，而平均度则会减小。通过添加额外的链接并设置  （其中  ）得到几何分支生长模型的膨胀版本，这种改进可以增加平均度或者至少可以避免平均度的快速减小。几何分支生长模型是积分重整化的统计逆过程（图1d），而膨胀几何分支生长模型则是收缩几何重整化（deflationary GR）的统计逆过程，其中剪掉链接的操作会减小平均度。加权和非加权的  模型的重整化能够准确复现真实网络中观察到的多尺度自相似性，这表明相同的原则能够在不同尺度上决定网络的长程和短程连接的连通性。

应用

几何重整化与几何分支生长模型的结合能够实现全尺度的网络自上而下的多尺度展开。其应用包括多尺度方法的设计，如提升单尺度方法性能的多尺度导航[68]。通过几何重整化方法可很方便地生成保持连接密度等统计特性的真实网络缩放副本[68,69]。这些副本能为研究真实网络中的尺寸依赖现象提供支持，在以下方面具有重要应用前景：探究尺寸诱导的随机共振效应、通过有限尺度标度技术分析临界行为69，以及对计算密集型过程进行高保真模拟的模型降阶。




拉普拉斯网络重整化




复杂网络重整化的另一方法[35,108]是利用节点间的拉普拉斯扩散概念[109,110]通过实时检测多尺度结构而实现顶点和边的粗粒化，并最终重整化网络上的动力学模型。与前述几何方法类似，该框架可基于直观且物理可实现的实空间版本而建立，这类似于统计物理中的Migdal-Kadanoff重整化群方法[111,112]，但其独特之处在于遵循了Wilson重整化群思想[113]而建立在严格对偶空间或者  空间表述之上。这两种表述均通过迭代方式粗粒化网络，同时在相当大的尺度范围内能够保持扩散动力学性质。

将拉普拉斯扩散视为近邻检测

构建异构无向网络(二值或加权)的拉普拉斯重整化群（Laplacian renormalization group，LRG）方法的第一步骤是利用对称图拉普拉斯算子[110,114]  定义节点在固定尺度下的“等效”邻域。该算子在初始层级  由邻接矩阵  构造，其矩阵元素为  ，其中  为Kronecker  符号，  表示节点  的度(  )。

设  代表定义在网络上的扩散场在时刻  的值，并记  为节点  的分量，假设其遵循热扩散方程  ，则可形式化表示为

其中扩散演化算子  。矩阵元素  给出了该场在时间  内从节点  到  (及反向)通过所有可能路径发生的扩散的比例[115,116]。

设  的特征值为  (满足  )，对应特征向量为  。对于连通无向网络，所有特征值非负且仅含一个零特征值，且可将特征向量正交归一化。  共享了特征值为  的特征向量。参数  可视为网络尺度度量：较大  对应扩散连接的更大邻域。例如对格点来说，每个  对应空间尺度  (  为扩散常数)，此时  在每个时间  都诱导了网络的一个最优划分[117]。

实空间中的拉普拉斯重整化群

基于物理诠释，可利用  将原始网络(  )的  个节点在任意时刻  下划分为  个“扩散等效”的子图，继而粗粒化为超节点以定义下一层级(  )网络。通过对微观小尺度连边关系的剪裁来确定超节点间重整化后的边(如公式(1)(3))。对于规则格点，固定  就等价于固定空间尺度  ，此过程完全可以类比于Ising模型中的Kadanoff块自旋方法[118]。

网络的拉普拉斯粗粒化方法可概括如下。首先定义二值化拉普拉斯矩阵  ，其元素为：

若其他情况

需注意  是  的单位矩阵，且对所有  有  。对固定的  ，矩阵  可视为原网络的超图的邻接矩阵，其包含  个在尺度  上通过扩散连接的连通分支。此过程将原来的  个节点划分为  个超节点（图2a）。  越大，连通分支数量越少且每个连通分支的规模越大。  意味着仅存在单一分支，也就是说，因均匀扩散场最终所有网络节点均连接在一起。基于方程(3)的粗粒化加权邻接矩阵  可通过定义超节点间的加权超边来构造，其权重等于连接两对应细尺度簇的微边权重经适当归一化后的总和（图2b）。亦可采用统计物理粗粒化中的一致性裁剪方法获取二值邻接矩阵  （例如通过方程(1)）。整个过程可迭代执行以定义更高层级  （图2c,d）。


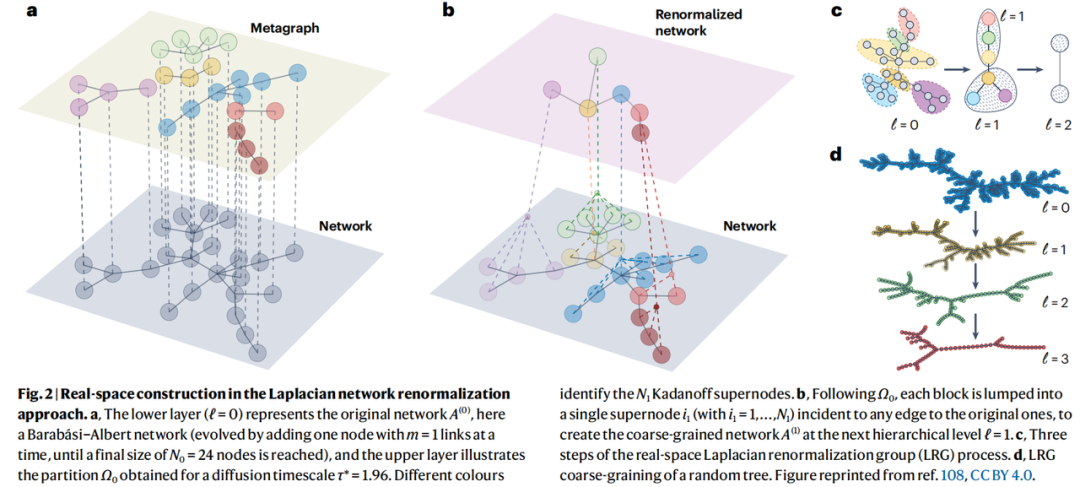
图2  实空间中的拉普拉斯网络重整化方法的构造。 a. 底层 (  ) 表示原始网络  （此处为 Barabási-Albert 网络，通过每次添加一个带  条连接的节点演化而成，最终规模为  个节点），上层展示扩散时间尺度  对应的划分  。不同颜色标识  个 Kadanoff 超节点。 b. 基于  ，每个块被聚合为单个超节点  （  ），保留与原节点连接的边，从而在下一层级  构建粗粒化网络  。 c. 实空间拉普拉斯重整化群（LRG）过程的三个步骤。 d. 随机树的 LRG 粗粒化。图转载自文献[108]，遵循 CCBY 4.0 协议。

k-空间上的拉普拉斯重整化群

该公式化过程能够与Wilson在连续场论中的重整化群方法直接类比[119]，可以显式地体现出其半群性质。它可视为实空间拉普拉斯重整化群在傅里叶空间的对应，其中傅里叶基由拉普拉斯特征向量给出，波模态由拉普拉斯特征值替代。在规则格点上，这些特征向量确实与平面波傅里叶基一致，其特征值简化为  。

该方法为重整化过程提供更深刻的洞见，不仅允许网络粗粒化，还能恰当的重标度嵌入其中的统计动力学模型（如Ising模型或切触过程）以探测和研究特征（关联）尺度及可能的相变。由于  与  是厄米算子（注：数学上通常称为自伴算子），我们采用量子力学“bra-ket”符号书写：

特征向量的完备性保证了粗粒化变量定义的合理性。后续步骤按Wilson范式[113]实现重整化程序：

  • 设定时间  以确定新分辨率尺度（或低能截断）

  • 将拉普拉斯谱划分为两类：  个“快”特征值  ，以及  个“慢”特征值 

  • 积掉谱的“快”(  )区域，重定义慢特征向量贡献的截断拉普拉斯算子  。这对英语重整化方法的第二步。

  • 重新计算时间标度  ，使  ，作为新的时间单位，对应粗粒化拉普拉斯算子重整化至层级  ，  。这对应于重整化方法的第三步。

迭代这些步骤可生成聚合所有层级  的重整化拉普拉斯算子  。该拉普拉斯重整化群的  空间公式可与实空间解释互为补充（见附录）。

Ising 模型、接触过程以及大多数以规则格点上局部平移不变相互作用为特征的统计模型的统计场表述，都允许高斯近似，其核完全由拉普拉斯算子决定，该算子在格点上的拉普拉斯平面波基下的矩阵是对角的[120,121]。对于不规则网络上的相同模型[34,122,123]这一点仍然成立，唯一的区别是拉普拉斯算子不再具有平移不变性。这种高斯近似在所有情况下都是唯一精确可解的场论，非高斯相互作用通常需要通过围绕它的微扰法来研究。这是 Wilson 重整化群的关键点之一：傅里叶基是在精确可解的高斯近似下能使矩阵为对角矩阵的基，即这些状态是由线性无关且正交的变量的叠加决定。因此，当研究非高斯项的变换的细节时，尺度变换（缩放）在利用高斯近似的基坐标中以直接重参数化进行的。拉普拉斯重整化群能够将其视为统计模型的非局部和异质嵌入空间，从而将这种方法推广到不规则网络的情形。

最后，网络单纯复形上的拉普拉斯算子的谱维数也有所研究[124,125]，并且拉普拉斯重整化群也可以推广到由单纯复形和高阶相互作用构建的网络中[126,127]（见附录）。

扩散演化算子的统计物理学解释

算子  可用于构建网络的“本征尺度扫描仪”。该“扫描仪”具备平衡态统计物理中熵敏感性或热容的全部数学特性，其显著极大值（在无限尺寸极限下发散）能够表明网络结构组织中的一类相变。具体而言，  的特征值  可用来定义实时的概率密度函数  ，其中配分函数  ，  为狄拉克δ函数。该测度对应的香农熵为  。由于无向网络的  为厄米且半正定，  可形式化视为冯·诺依曼熵  ，与量子正则密度算子  相关联（参考文献109,128,129），此处  扮演哈密顿量角色，  则对应逆温度[130,131]。等价地，配分函数  通过  与自由能相关联。

该形式类比的直接推论是下述量

具有熵敏感性的数学特性，因而是个热容[15,129]。在节点数无穷大的极限下，相变点可解释为  在呕血尺度  处的奇异性或虽有限但  值非常大的情形。换言之，  是网络拓扑发生突变的内蕴尺度，类似于Ising模型中关联长度尺度的作用。例如，在具有相同尺寸的块构成的网络模型，要求块内部稠密连接但是块之间相互连接较弱[132]，在这个模型中  呈现双峰：一个对应于单块的扩散尺度，另一个对应于块间典型路径的更大尺度。在此意义上，  可作为本征尺度探测器，通过识别网络结构发生拓扑转变的特征尺度来诱导网络的粗粒化过程[132]。

拓扑标度不变网络

当  时网络具有拓扑标度不变性，其中  是拉普拉斯特征值密度，  和  为拉普拉斯谱维度[133]（见附录）。此时熵敏感性与  无关，保持恒定值  [35]。这种  无关性会在规则格点或随机树中出现，也存在于更复杂网络如分层模块化网络[134]中。根据本节讨论的拉普拉斯重整化群的额定义，所有拓扑尺度不变网络在拉普拉斯尺度变换和粗粒化下保持相同拓扑结构[135]（另见[136]）。因此，  可作为实际网络尺度不变性的探测器，若其为常数值则可直接用于度量谱维度。




多尺度网络的重整化




多尺度网络重整化方法[137–139] 旨在引入在任意节点聚合下保持一致的随机图模型。其动机源于两个相关的考虑。一方面，对于给定的网络，不同的节点划分可能因不同原因而具有相关性，例如，本文中讨论的多种方法可能会产生不同的节点粗粒化方式，因此，需要在多种可能的节点聚合方式下对同一系统进行一致建模。另一方面，在真实世界的网络数据中，“节点”的含义并非总是同质的，也就是说，有时尽管大多数节点代表某个层级上观察到的系统单元（例如制造生产网络中的单个公司），但其他节点却可能代表更粗层级的聚合（例如整个行业或国家，每个都聚合体了多家公司）。这两种场景提示，所研究的系统应拥有一个唯一的随机图模型，该模型在任意节点聚合（或节点拆解）后仍能够具备一致性（即生成一致的图概率分布）。

这一要求意味着，多尺度重整化方法应当对粗粒化变量的定义保持完全不可知，也就是说，人们可以任意“平铺”节点集，引入任何所需的划分  ，而不依赖于度量或扩散邻近性的概念。对于平均掉细微细节的过程，原则上该方法应允许不同的选择，但具体而言，考虑到某些应用中构成节点（如单个公司）之间的任何连接对定义超节点（如国家或经济部门）之间的联系具有重要性，因此选择了方程 (2) 中的方案[137]。无论如何，多尺度方法的独特之处在于识别出重整化群流的不动点，在该不动点上可以对任意节点聚合方式进行耦合系数和参数值的精确重整化，本节将对此进行阐释。

节点聚合下的不变性

所求的聚合不变随机图概念在思想上类似于稳定随机变量[140-142]，即组合后仍服从相同分布的随机变量（例如求和[141,142]或取极大值后[143,144]）。此处使用在粗粒化方法小节末尾所引入的符号：考虑以概率  生成具体实现  的随机图系综，其中  是模型所有参数的集合。给定概率分布  和任意划分  ，可在高一层级  导出结果一个图系综由特定概率分布  描述（图3a）。多尺度重整化方法[147]的核心思想是：识别在所有层次和所有可能的划分下保持不变的图概率分布函数的形式（因此可从  中省略下标  ）。只有（重整化）参数  允许依赖层级  ，且通常是通过  与  关联。该条件对应于通过在图概率空间中识别重整化群流不动点来实现参数的精确重整化。


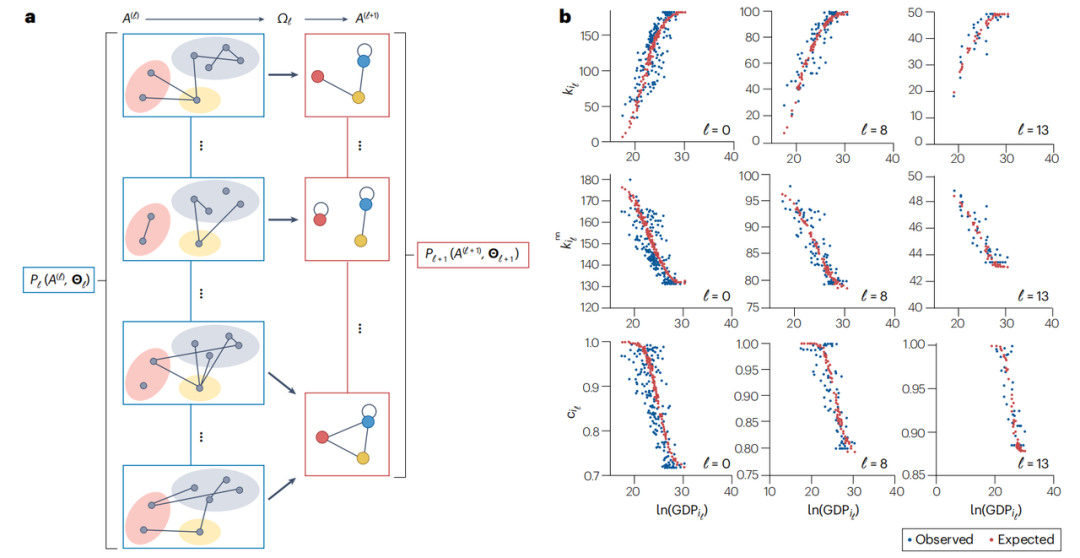
图3  多尺度网络重整化方法。 a. 给定邻接矩阵为  、参数集为  的图概率分布  ，节点划分  将节点集映射到粗粒化邻接矩阵  的“块节点”上。若存在从  到  的连接（其中  ），则绘制该连接。需注意，层级  的多个图可能在层级  合并为同一图，因此粗粒化将诱导下一层级图的新概率分布  。多尺度方法旨在寻找该概率的尺度不变形式。 b. 基于多尺度模型预测重整化国际贸易网络在不同地理聚合层级的局域拓扑性质。首行展示三个代表性层级（  ，对应  （左）、  （中）、  （右））中所有  个节点的观测与预测度值  随  的变化。中间行对应相同层级下所有节点的观测与预测最近邻平均度  。末行展示相同条件下局域聚类系数  的观测与预测值。GDP 表示国内生产总值。图转载自文献[137]，遵循 CC BY 4.0 协议。

带独立边的多尺度模型

对于带独立边的图模型，可以找到显式不动点  。这类模型的概率分布可分解为节点对  的连接概率  ：

多尺度模型（multiscale model，MSM）[137]可定义为连接概率空间中重整化群流的唯一非平凡不动点，即在方程(2)下满足尺度不变性要求的解：

其中参数  被分解为如下参数：全局参数  调节网络整体连接密度，  个正定节点特异性加性参数  （称为“适应度”值）决定节点建立连接的个体倾向，以及（可选）  个二元参数  表示节点对效应（如节点相似性、距离或共同社区成员资格）。函数  是任意单调正值函数。

参数重整化与聚合不变性

当使用划分  将网络粗粒化至  层级时，构型  的概率仍精确由方程(10)和(11)描述，其中  替换为  且参数重整化为：

其中  具有尺度不变性，即重整化过程中保持不变。（注：此处原文可能有笔误，这里添加了一个  。）

当  为超度量时（即  可表示为树图中节点  和  到其共同分支点的距离，其中节点为叶节点），重整化后仍保持超度量性：对任意  和  ，有  （参考文献137）。另一特例是，令  可消去所有二元效应（dyadic effects），使模型完全由适应度驱动。关键的是，适应度参数本身不可消去，代表模型中不可约简的特征。

值得注意的是，方程(11)对应的配分函数  是可以精确计算的，并可以证明其在任意计算层级取值相同[137]，这证实了多尺度模型位于重整化流的不动点上（见附录）。与之前讨论的几何或拉普拉斯方法不同，多尺度模型既不需要带节点坐标的度量空间嵌入，也不需要扩散邻近性概念来进行重整化。实际上，该模型允许任意划分，其聚合不变性相对于邻近驱动的尺度不变性也更加显著。

多尺度模型可以推广至加权[145]和定向[139]网络。定向网络的推广是直接的：由于模型不依赖几何距离（但是必须要求对称，尽管定向网络具有通常不对称性），可通过为每个节点添加另一个适应度变量处理定向网络。为每个节点增加第三个适应度参数后，模型还能描述非平凡的互利度（reciprocity）[109]，从而能建模真实世界的有向网络[100-109]。更一般地，适应度变量  可以是任意维向量，上述表达式中的乘积  可解释为内积[100,101]。

真实世界网络重整化的淬火变体

在多尺度模型的“淬火”变体中，可以将节点适应度解释为某种确定性的属性，例如观测量或潜在的节点特征等[137,139,150,151]。因此该变体可用于对真实世界的网络进行基于经验量的显式建模（如适应度模型族[152]），或基于潜在变量的建模（如节点嵌入算法族[153]）。然而，这些算法族的通用模型是在固定分辨率层级构建的，而多尺度模型要求通过重整化参数在所有聚合层级一致描述同一系统，即保持相同连接概率。因此，这是唯一在聚合后仍保持适应度模型特征的适应度可加性模型[137,150]，同时也是在任意粗粒化下生成一致节点嵌入的方法[151]。

该模型在多个层级成功复现了国际贸易网络[137,139]（适应度对应于各国经验GDP，二元因子对应于  描述的地理距离）、企业间网络[150]和投入产出网络[151]（外向/内向适应度分别定义为公司/行业总产出/总投入，  ）的特性。当二元和/或适应度量从数据输入时，仅剩全局参数作为自由参数。该参数可在特定分辨率层级拟合，同时提供所有其他层级的预测。这些多尺度预测与多层级经验网络特性高度吻合[137,139,150]（图3b）。

需注意该模型能在极端非均匀的情况下解决聚合方案（其他方法在此类情形下失效）：例如在生产网络中，部分节点可代表某一欧盟国家的独立企业，其他节点可代表剩余欧盟国家整体（各国企业被聚合为单一节点），而“世界其他地区”节点则可代表所有非欧盟国家的聚合体[150]。

当然，对于一般真实网络，并不能保证存在可与多尺度模型中加性适应度变量对应的经验节点特征。在此情形下，适应度变量可视为需优化拟合的自由参数（通常为给定维度的向量），其拟合仅依赖于经验网络的结构信息[151]。此过程生成抽象向量空间中的节点嵌入表示，其向量和对应节点的合并操作[151]。该方向的开放性挑战仍在于确定嵌入向量的最优维度及其唯一性问题。

集群无标度网络与细粒度化的退火变体

在退火变体[137,138]中，将节点适应度视为随机变量，类似于非均匀随机图家族的情况[154]。因此，它作为一个“隐”变量，不与任何特定的真实世界特征相关联。在这种方法中，聚合不变性的要求也适用于适应度：在任何层次级别  ，人们应当能从相同的概率密度函数中抽取节点适应度，而无需“知道”它们在更细层次上的值（或密度函数）。由于适应度具有加性，这一要求立即表明它应为  -稳定随机变量[141]，意味着其密度函数在大  时衰减为  。为确保适应度的必要正性，指数需在  范围内，这导致适应度的均值（及所有更高阶矩）发散。在此范围内，唯一已知的  -稳定分布为Lévy分布（  ），但对于任意  值，人们都能推导出严格结果，且这些结果基本与  无关[138]。若将节点聚集成大小相等的块，适应度将保持相同的密度，仅需对全局参数进行重新缩放。在退火变体中，多尺度模型能生成任意大的网络，其性质确实可在节点数量发散的渐近极限下研究[138]。

适应度的无穷均值的特性使得退火多尺度模型的期望拓扑性质与具有有限均值适应度的类似模型产生的性质大不相同。特别地，人们能严格证明[137,138]，期望度分布  具有普适的幂律尾衰减  ，与  值无关。对于聚合到  个节点的层次  ，若  ，衰减表现为纯幂律[138]；对于更粗粒化的聚合，分布尾部会出现依赖密度的截断[137]。值得注意的是，退火模型展示了许多现实网络特性，包括衰减的同配性轮廓、在稀疏（密度消失）状态下消失的全局聚类系数，以及不消失的局部聚类系数。在其他稀疏边独立模型中，除非假设它们依赖度量距离，否则不会出现不消失的局部聚类系数。因此，无穷均值适应度即使无几何结构也能生成正局部聚类系数的发现，成为退火多尺度模型的重要洞见。

最后，由于  -稳定随机变量具有无限可分性（即它们可表示为来自同一家族的任意数量独立同分布（i.i.d.）随机变量之和），在退火方法中，人们能将节点无限细分为子节点，每个子节点拥有各自的i.i.d.适应度。这意味着在此情况下，重整化流不仅定义了一个自底向上的半群，还定义了一个双向进行的群[137]。一个公开挑战在于，如何将模型这一引人注目的理论特性转化为实用工具，以细化只能在粗粒化水平观察的现实网络，因为现实网络中的节点未必具有  -稳定变量的特性。




展望




尽管目前网络重整化的某些方法在构建几何与系综异质性的通用框架方面取得显著进展，但仍存在若干挑战与开放性问题，我们将在此讨论。

分辨率水平

真实世界的网络实现中，由于拓扑结构的异质性，因而将几何和拓扑的组织归于“功能单元”的操作具有相当挑战性。这比同质的格点或规则树的情况更为复杂。此外，在真实世界网络网络的不同表示形式中，定义节点的合理分辨率尺度通常并非是系统内蕴的固有性质，而是源于观测限制或数据聚合的粗糙程度。例如，保密性问题导致金融关系网络（如银行间借贷与风险敞口）和经济关系网络（如供应链）中的个体连接的信息无法获取，而人际接触数量对流行病网络的影响仅能部分可见。理想情况下，人们希望确定并区分网络属性固有的特征尺度与数据分辨率相关的尺度。

与动力学过程相容的重整化

对任意网络上的动力学结构和过程的重整化的主要挑战在于，如何使用与底层图结构和系综随机性的重整化相兼容的方式，来进行对动力学结构和过程进行重整化。此前研究这一问题的学者们仅限于探讨规则或分形格点上的动态过程，在这些规则格点中，粗粒化的结构部分能够相当自然地加以定义。

具体而言，精确的重整化群计算已应用于分形网络上的高斯场[155]和随机游走[156]，并扩展至研究Hanoi网络上Ising模型的不动点[157]，揭示出不同区域内独特的临界非普适行为。研究者利用裁剪技术探索了网络增长模型上渗流临界行为，发现其与无关联网络中观察到的行为存在偏差[158]。这些方法也用于分析真实世界的系统。例如，学者们为神经元网络中的活动开发了唯象的粗粒化程序，在将其应用于海马体细胞时，能够发现静态和动态的变量均呈现标度特征，表明网络群体行为中存在非平凡的不动点[159]。

一般而言，我们可以预期真实世界网络及其粗粒化版本中的结构异质性会导致动力学过程的重整化与拓扑结构的重整化之间存在耦合。然而开发独立于具体方案的框架，以兼容的方式同时重整化网络动态及底层几何或系综结构，仍是一项挑战。

广义临界性？

真实世界网络中连接的强异质性与非局部性可能影响动力学模型在临界点附近的局部激发与集体激发之间的转变性质。这些性质也可能引发更复杂的行为，从而需要更广义的临界性定义。例如在真实接触网络上的疫情传播动力学中，集体大流行态与局部地方病流行态间的转变可能比近似格点的理想化接触网络更为复杂。相互作用参数可能存在完整区域，使得其中临界行为在宏观但局部的集体子网络中逐步显现，此类参数区域的形成由强拓扑异质性及潜在层级结构决定。该现象表明，拓扑复杂性可能要求将临界点概念扩展至类似于Griffith相的范畴[160,161]

信息论视角下的参数相关性与无关性

粗粒化意味着信息丢失。这种丢失非但不是缺陷，反而是重整化群技术的核心工具，因为它能识别在最有价值的时空尺度参数，并在这个尺度上描述系统行为。重整化方法最初的设计目标就是用于研究具有大自由度的物理系统，并识别系统参数如何从微观流向宏观尺度。该跨尺度信息流的关键在于：随着尺度增大，某些参数对系统行为的相关性增强，而其他参数逐渐无关。在复杂网络背景下，探索自下而上研究这种信息随参数的流动，可为基于第一性原理理解哪些量和控制参数在最大时空尺度最重要提供重要价值。通过信息论（ Fisher 信息与应用于复杂系统的信息几何形式体系在），也可从纯经验视角获得互补的自上而下的方法。

物理系统中的参数相关性概念在场论及其流体动力学极限下是通过幂次计算可重整化概念体现的，该概念大致追踪了描述系统动力学所有可能项的导数展开。即，在理论空间中进行有效的泰勒展开，使得即时特征显现。在足够大尺度下，含高阶导数的项对物理观测量的贡献递减。从信息论视角看，这意味观测系综的结果更敏感地依赖于导数展开中主导阶项的系数。因此，参数相关性概念可直接转译为信息论量，且能推广至物理系统之外。这种转译不仅具有直接概念用途，更为识别和理解决定任意系统在大尺度行为的参数开辟通道——即使缺乏微观模型描述，或处理任意几何与系综随机性时亦然。


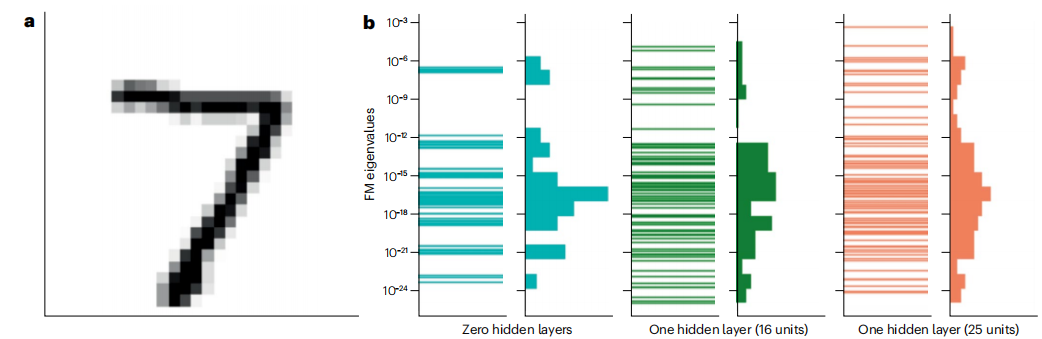
图4  信息论参数流。 a. MNIST（Modified National Institute of Standards and Technology）数据集中的手写数字“7”实例。 b. 成功分类 MNIST 数据集中左侧图像的30个训练神经网络的 Fisher 信息矩阵特征值（左图）及其分箱密度直方图（右图）。特征值呈现指数型层级结构，表明仅少量集体权重对训练网络精度起关键作用。图由 Leone Luzzatto 提供。

信息几何与参数流

给定任意数据集，可构建由假设模型生成的似然函数来描述该数据集。最大似然估计即为识别使该似然函数最大化的参数集，并将其作为对底层模型的最佳推断。对数似然相对于参数的二阶导数自然形成度量参数空间距离的度量结构，能够捕捉似然偏离最大值的变化方式。这种推断的几何化（称为信息几何[162]）使得在参数流的统一框架下重构统计（贝叶斯）推断与重整化成为可能[163]。

基于给定数据集构建的似然对应的 Fisher 信息度量具有显著的特征值层级结构。该层级意味着：最大特征值对应参数的微小变化对观测结果影响最大（图4），其意义直接映射至重整化群意义上的参数相关性概念——最相关参数对应最大特征值[164]。这解释了为何在系统信息有限时，简单模型常能异常有效地捕捉大部分相关特征。在训练用于手写数字识别的神经网络中（图4）， Fisher 信息的最大特征值对应的集体权重几乎完全决定训练网络的测试精度，其余参数与权重组合基本无关。轻量化的模型框架[165]也能够通过 Fisher 信息特征值的层级结构识别这些参数。

当对网络数据集或模型嵌入的模拟的实现进行不断的粗粒化后，粗粒化的似然函数产生的部分特征值相关性增强而另一部分的相关性减弱，此过程与重整化群相关性精确对应。基于此，仅通过研究数据不断粗粒化下的参数流，即可系统推断不同相与控制参数的存在，此处唯一的假设是粗粒化方案选择、底层的几何/系综随机性的参数化方式及其先验分布的设定。该方法已用于识别异质性化学系统的不同相[166]，在复杂网络背景下亦具研究前景。


参考文献


  1. Pósfai, M. & Barabási, A.-L. Network Science (Cambridge Univ. Press, 2016).

  2. Squartini, T. & Garlaschelli, D. Maximum-Entropy Networks: Pattern Detection, Network Reconstruction and Graph Combinatorics (Springer, 2017).

  3. Newman, M. Networks (Oxford Univ. Press, 2018).

  4. Cimini, G. The statistical physics of real-world networks. Nat. Rev. Phys. 1 (2019).

  5. Radicchi, F., Ramasco, J., Barrat, A. & Fortunato, S. Complex networks renormalization: flows and fixed points. Phys. Rev. Lett. 101 (2008).

  6. Radicchi, F., Barrat, A., Fortunato, S. & Ramasco, J. J. Renormalization flows in complex networks. Phys. Rev. E 79 (2009).

  7. Chen, D., Su, H., Wang, X., Pan, G.-J. & Chen, G. Finite-size scaling of geometric renormalization flows in complex networks. Phys. Rev. E 104 (2021).

  8. Chen, D., Cai, D. & Su, H. Scaling properties of scale-free networks in degree-thresholding renormalization flows. IEEE Trans. Netw. Sci. Eng. 10 (2023).

  9. Serafino, M. True scale-free networks hidden by finite size effects. Proc. Natl Acad. Sci. USA 118 (2021).

  10. Itzykson, C. & Drouffe, J. M. Statistical Field Theory: Volume 1, From Brownian Motion to Renormalization and Lattice Gauge Theory (Cambridge Univ. Press, 1989).

  11. Burgess, C. P. Introduction to Effective Field Theory (Cambridge Univ. Press, 2020).

  12. Bardoscia, M. The physics of financial networks. Nat. Rev. Phys. 3 (2021).

  13. Soriano-Paños, D. Modeling communicable diseases, human mobility, and epidemics: a review. Ann. Phys. 534 (2022).

  14. Song, C., Havlin, S. & Makse, H. A. Self-similarity of complex networks. Nature 433 (2005).

  15. Binder, K. & Young, A. P. Spin glasses: experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 58 (1986).

  16. Bar-Yam, Y. & Patil, S. P. Renormalization of sparse disorder in the Ising model. Preprint at arXiv (2018).

  17. Mandelbrot, B. B. The Fractal Geometry of Nature Vol. 2 (Freeman, 1982).

  18. Samsel, M., Makulski, K., Łepek, M., Fronczak, A. & Fronczak, P. Towards fractal origins of the community structure in complex networks: a model-based approach. Preprint at arXiv (2023).

  19. Goh, K.-I., Salvi, G., Kahng, B. & Kim, D. Skeleton and fractal scaling in complex networks. Phys. Rev. Lett. 96 (2006).

  20. Kim, J. S., Goh, K.-I., Kahng, B. & Kim, D. Fractality and self-similarity in scale-free networks. New J. Phys. 9 (2007).

  21. Fronczak, A. Scaling theory of fractal complex networks. Sci. Rep. (2024).

  22. Song, C., Havlin, S. & Makse, H. A. Origins of fractality in the growth of complex networks. Nat. Phys. 2 (2006).

  23. Rozenfeld, H. D., Song, C. & Makse, H. A. Small-world to fractal transition in complex networks: a renormalization group approach. Phys. Rev. Lett. 104 (2010).

  24. Newman, M. & Watts, D. Renormalization group analysis of the small-world network model. Phys. Lett. A 263 (1999).

  25. Kim, B. J. Geographical coarse graining of complex networks. Phys. Rev. Lett. 93 (2004).

  26. Gfeller, D. & Los Rios, P. Spectral coarse graining of complex networks. Phys. Rev. Lett. 99 (2007).

  27. Wang, Y., Zeng, A., Di, Z. & Fan, Y. Spectral coarse graining for random walks in bipartite networks. Chaos 23 (2013).

  28. Gfeller, D. & Los Rios, P. Spectral coarse graining and synchronization in oscillator networks. Phys. Rev. Lett. 100 (2008).

  29. Chen, J., an Lu, J., Lu, X., Wu, X. & Chen, G. Spectral coarse graining of complex clustered networks. Commun. Nonlinear Sci. Numer. Simul. 18 (2013).

  30. Jia, Z., Zeng, L., Wang, Y.-Y. & Wang, P. Optimization algorithms for spectral coarse-graining of complex networks. Physica A 514 (2019).

  31. Zeng, A. & Lü, L. Coarse graining for synchronization in directed networks. Phys. Rev. E 83 (2011).

  32. Wang, P. & Xu, S. Spectral coarse grained controllability of complex networks. Physica A 478 (2017).

  33. Aygün, E. & Erzan, A. Spectral renormalization group theory on networks. J. Phys. Conf. Ser. 319 (2011).

  34. Tuncer, A. & Erzan, A. Spectral renormalization group for the Gaussian model and $Psi$4 theory on nonspatial networks. Phys. Rev. E 92 (2015).

  35. Villegas, P., Gili, T., Caldarelli, G. & Gabrielli, A. Laplacian renormalization group for heterogeneous networks. Nat. Phys. 19 (2023).

  36. Chen, H., Hou, Z., Xin, H. & Yan, Y. Statistically consistent coarse-grained simulations for critical phenomena in complex networks. Phys. Rev. E 82 (2010).

  37. Long, Y.-S., Jia, Z. & Wang, Y.-Y. Coarse graining method based on generalized degree in complex network. Physica A 505 (2018).

  38. Wang, Y. Coarse graining method based on node similarity in complex network. Commun. Netw. 10 (2018).

  39. Lorrain, F. & White, H. C. Structural equivalence of individuals in social networks. J. Math. Sociol. 1 (1971).

  40. Dunne, J. A. Food webs. In textit{Encyclopedia of Complexity and Systems Science (ed. Meyers, R.) 3661–3682 (Springer, 2009).

  41. Itzkovitz, S. Coarse-graining and self-dissimilarity of complex networks. Phys. Rev. E 71 (2005).

  42. Serrano, M. Á., Krioukov, D. & Boguñá, M. Self-similarity of complex networks and hidden metric spaces. Phys. Rev. Lett. 100 (2008).

  43. Alvarez-Hamelin, J., Dall’Asta, L., Barrat, A. & Vespignani, A. K-core decomposition of Internet graphs: hierarchies, self-similarity and measurement biases. Netw. Heterog. Media 3 (2008).

  44. Lambiotte, R. Multi-scale modularity in complex networks. In textit{8th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks 546–553 (IEEE, 2010).

  45. Karypis, G. & Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 20 (1998).

  46. Abou-Rjeili, A. & Karypis, G. Multilevel algorithms for partitioning power-law graphs. In textit{Proc. 20th IEEE International Parallel & Distributed Processing Symposium (IEEE, 2006).

  47. Leifer, I., Phillips, D., Sorrentino, F. & Makse, H. A. Symmetry-driven network reconstruction through pseudobalanced coloring optimization. J. Stat. Mech. 2022 (2022).

  48. Boldi, P. & Vigna, S. Fibrations of graphs. Discrete Math. 243 (2002).

  49. Cardelli, L., Tribastone, M., Tschaikowski, M. & Vandin, A. Maximal aggregation of polynomial dynamical systems. Proc. Natl Acad. Sci. USA 114 (2017).

  50. Cardelli, L., Tribastone, M., Tschaikowski, M. & Vandin, A. Erode: a tool for the evaluation and reduction of ordinary differential equations. In textit{Proc. Tools and Algorithms for the Construction and Analysis of Systems: 23rd International Conference, TACAS 2017 Part II 23, 310–328 (Springer, 2017).

  51. Argyris, G. A., Lluch Lafuente, A., Tribastone, M., Tschaikowski, M. & Vandin, A. Reducing Boolean networks with backward equivalence. BMC Bioinformatics 24 (2023).

  52. Morone, F., Leifer, I. & Makse, H. A. Fibration symmetries uncover the building blocks of biological networks. Proc. Natl Acad. Sci. USA 117 (2020).

  53. Gili, T. et al. Fibration symmetry-breaking supports functional transitions in a brain network engaged in language. Preprint at arXiv (2024).

  54. Papadopoulos, F., Psounis, K. & Govindan, R. Performance preserving topological downscaling of internet-like networks. IEEE J. Sel. Areas Commun. 24 (2006).

  55. Papadopoulos, F. & Psounis, K. Efficient identification of uncongested internet links for topology downscaling. SIGCOMM Comput. Commun. Rev. 37 (2007).

  56. Di, X., Zhao, Y., Huang, S. & Liu, H. X. A similitude theory for modeling traffic flow dynamics. IEEE Trans. Intell. Transp. Syst. 20 (2019).

  57. Chen, H., Perozzi, B., Hu, Y. & Skiena, S. HARP: hierarchical representation learning for networks. In textit{Proc. 32nd AAAI Conference on Artificial Intelligence/30th Innovative Applications of Artificial Intelligence Conference/8th AAAI Symposium on Educational Advances in Artificial Intelligence (AAAI’18/IAAI’18/EAAI’18) 2127–2134 (AAAI, 2018).

  58. Loukas, A. Graph reduction with spectral and cut guarantees. J. Mach. Learn. Res. 20 (2019).

  59. Jin, Y., Loukas, A. & JaJa, J. Graph coarsening with preserved spectral properties. In textit{Proc. International Conference on Artificial Intelligence and Statistics 4452–4462 (PMLR, 2020).

  60. Fahrbach, M., Goranci, G., Peng, R., Sachdeva, S. & Wang, C. Faster graph embeddings via coarsening. In textit{Proc. International Conference on Machine Learning 2953–2963 (PMLR, 2020).

  61. Liang, J., Gurukar, S. & Parthasarathy, S. MILE: A multi-level framework for scalable graph embedding. In textit{Proc. International AAAI Conference on Web and Social Media Vol. 15, 361–372 (AAAI, 2021).

  62. Huang, Z., Zhang, S., Xi, C., Liu, T. & Zhou, M. Scaling up graph neural networks via graph coarsening. In textit{Proc. 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining 675–684 (ACM, 2021).

  63. Zhang, Z., Ghavasieh, A., Zhang, J. & De Domenico, M. Coarse-graining network flow through statistical physics and machine learning. Nat. Commun. 16 (2025).

  64. Yedidia, J. S. & Bouchaud, J.-P. Renormalization group approach to error-correcting codes. J. Phys. A 36 (2003).

  65. Klein, B. & Hoel, E. The emergence of informative higher scales in complex networks. Complexity 2020 (2020).

  66. Faccin, M., Schaub, M. T. & Delvenne, J.-C. Entrograms and coarse graining of dynamics on complex networks. J. Complex Netw. 6 (2017).

  67. Boguñá, M. Network geometry. Nat. Rev. Phys. 3 (2021).

  68. García-Pérez, G., Boguñá, M. & Serrano, M. Á. Multiscale unfolding of real networks by geometric renormalization. Nat. Phys. 14 (2018).

  69. Zheng, M., García-Pérez, G., Boguñá, M. & Serrano, M. Á. Scaling up real networks by geometric branching growth. Proc. Natl Acad. Sci. USA (2021).

  70. Zheng, M., García-Pérez, G., Boguñá, M. & Serrano, M. Á. Geometric renormalization of weighted networks. Commun. Phys. 7 (2024).

  71. Kolk, J., Serrano, M. & Boguñá, M. Renormalization of networks with weak geometric coupling. Phys. Rev. E 110 (2024).

  72. Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A. & Boguñá, M. Hyperbolic geometry of complex networks. Phys. Rev. E 82 (2010).

  73. Gilbert, E. N. Random plane networks. J. Soc. Indust. Appl. Math. 9 (1961).

  74. Penrose, M. Random Geometric Graphs Vol. 5 (Oxford Univ. Press, 2003).

  75. Hoff, P. D., Raftery, A. E. & Handcock, M. S. Latent space approaches to social network analysis. J. Am. Stat. Assoc. 97 (2002).

  76. Boguñá, M., Krioukov, D., Almagro, P. & Serrano, M. Á. Small worlds and clustering in spatial networks. Phys. Rev. Res. 2 (2020).

  77. Kolk, J., Serrano, M. Á. & Boguñá, M. An anomalous topological phase transition in spatial random graphs. Commun. Phys. 5 (2022).

  78. Kolk, J., Serrano, M. Á. & Boguñá, M. Random graphs and real networks with weak geometric coupling. Phys. Rev. Res. 6 (2024).

  79. García-Pérez, G., Allard, A., Serrano, M. Á. & Boguñá, M. Mercator: uncovering faithful hyperbolic embeddings of complex networks. New J. Phys. 21 (2019).

  80. Jankowski, R., Allard, A., Boguñá, M. & Serrano, M. Á. The D-Mercator method for the multidimensional hyperbolic embedding of real networks. Nat. Commun. 14 (2023).

  81. Boguñá, M., Papadopoulos, F. & Krioukov, D. Sustaining the internet with hyperbolic mapping. Nat. Commun. 1 (2010).

  82. Gugelmann, L., Panagiotou, K. & Peter, U. Random hyperbolic graphs: degree sequence and clustering. In textit{Proc. Automata, Languages and Programming, 39th International Colloquium (ICALP 2012) (eds Czumaj, A. et al.) 573–585 (Springer, 2012).

  83. Candellero, E. & Fountoulakis, N. Clustering and the hyperbolic geometry of complex networks. Internet Math. 12 (2016).

  84. Fountoulakis, N., Hoorn, P., Müller, T. & Schepers, M. Clustering in a hyperbolic model of complex networks. Electron. J. Probab. 26 (2021).

  85. Abdullah, M. A., Fountoulakis, N. & Bode, M. Typical distances in a geometric model for complex networks. Internet Math. (2017).

  86. Friedrich, T. & Krohmer, A. On the diameter of hyperbolic random graphs. SIAM J. Discrete Math. 32 (2018).

  87. Müller, T. & Staps, M. The diameter of KPKVB random graphs. Adv. Appl. Probab. 51 (2019).

  88. Serrano, M. Á., Krioukov, D. & Boguñá, M. Percolation in self-similar networks. Phys. Rev. Lett. 106 (2011).

  89. Fountoulakis, N. & Müller, T. Law of large numbers for the largest component in a hyperbolic model of complex networks. Ann. Appl. Probab. 28 (2018).

  90. Bianconi, G. & Ziff, R. Topological percolation on hyperbolic simplicial complexes. Phys. Rev. E 98 (2018).

  91. Kiwi, M. & Mitsche, D. Spectral gap of random hyperbolic graphs and related parameters. Ann. Appl. Probab. 28 (2018).

  92. Papadopoulos, F., Kitsak, M., Serrano, M. Á., Boguñá, M. & Krioukov, D. Popularity versus similarity in growing networks. Nature 489 (2012).

  93. Allard, A., Serrano, M. Á., García-Pérez, G. & Boguñá, M. The geometric nature of weights in real complex networks. Nat. Commun. 8 (2017).

  94. Serrano, M. Á., Boguñá, M. & Sagués, F. Uncovering the hidden geometry behind metabolic networks. Mol. Biosyst. 8 (2012).

  95. Kitsak, M., Papadopoulos, F. & Krioukov, D. Latent geometry of bipartite networks. Phys. Rev. E 95 (2017).

  96. Budel, G. & Kitsak, M. Complementarity in complex networks. Preprint at arXiv (2023).

  97. Kleineberg, K.-K., Boguñá, M., Serrano, M. Á. & Papadopoulos, F. Hidden geometric correlations in real multiplex networks. Nat. Phys. 12 (2016).

  98. Kleineberg, K.-K., Buzna, L., Papadopoulos, F., Boguñá, M. & Serrano, M. Á. Geometric correlations mitigate the extreme vulnerability of multiplex networks against targeted attacks. Phys. Rev. Lett. 118 (2017).

  99. Zuev, K., Boguñá, M., Bianconi, G. & Krioukov, D. Emergence of soft communities from geometric preferential attachment. Sci. Rep. 5 (2015).

  100. García-Pérez, G., Serrano, M. Á. & Boguñá, M. Soft communities in similarity space. J. Stat. Phys. 173 (2018).

  101. Muscoloni, A. & Cannistraci, C. V. A nonuniform popularity-similarity optimization (nPSO) model to efficiently generate realistic complex networks with communities. New J. Phys. 20 (2018).

  102. Allard, A., Serrano, M. Á. & Boguñá, M. Geometric description of clustering in directed networks. Nat. Phys. 20 (2024).

  103. Aliakbarisani, R., Ángeles Serrano, M. & Boguñá, M. Feature-enriched hyperbolic network geometry. Preprint at arXiv (2023).

  104. Zheng, M., Allard, A., Hagmann, P., Alemán-Gómez, Y. & Serrano, M. Á. Geometric renormalization unravels self-similarity of the multiscale human connectome. Proc. Natl Acad. Sci. USA 117 (2020).

  105. Barrat, A., Barthelemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA 101 (2004).

  106. Serrano, M. Á., Boguñá, M. & Pastor-Satorras, R. Correlations in weighted networks. Phys. Rev. E 74 (2006).

  107. Nolan, J. P. Univariate Stable Distributions: Models for Heavy Tailed Data (Springer Nature, 2019).

  108. Caldarelli, G., Gabrielli, A., Gili, T. & Villegas, P. Laplacian renormalization group: an introduction to heterogeneous coarse-graining. J. Stat. Mech. 2024 (2024).

  109. Domenico, M. & Biamonte, J. Spectral entropies as information-theoretic tools for complex network comparison. Phys. Rev. X 6 (2016).

  110. Masuda, N., Porter, M. A. & Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 716 (2017).

  111. Kadanoff, L. P. Notes on Migdal’s recursion formulas. Ann. Phys. 100 (1976).

  112. Migdal, A. A. Phase transitions in gauge and spin-lattice systems. Zh. Eksp. Teor. Fiz. 69 (1975).

  113. Wilson, K. G. & Kogut, J. The renormalization group and the $$varepsilo$$ expansion. Phys. Rep. 12 (1974).

  114. Newman, M. E. J. Networks: An Introduction (Oxford Univ. Press, 2010).

  115. Moretti, P. & Zaiser, M. Network analysis predicts failure of materials and structures. Proc. Natl Acad. Sci. USA 116 (2019).

  116. Burioni, R. & Cassi, D. Random walks on graphs: ideas, techniques and results. J. Phys. A 38 (2005).

  117. Villegas, P., Gabrielli, A., Poggialini, A. & Gili, T. Multi-scale Laplacian community detection in heterogeneous networks. Phys. Rev. Res. 7 (2025).

  118. Kadanoff, L. P. Scaling laws for Ising models near Tc. Phys. Phys. Fiz. 2 (1966).

  119. Wilson, K. G. Problems in physics with many scales of length. Sci. Am. 241 (1979).

  120. Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49 (2000).

  121. Dornic, I., Chaté, H. & Muñoz, M. A. Integration of Langevin equations with multiplicative noise and the viability of field theories for absorbing phase transitions. Phys. Rev. Lett. 94 (2005).

  122. Burioni, R. & Cassi, D. Geometrical universality in vibrational dynamics. Mod. Phys. Lett. B 11 (1997).

  123. Cassi, D. Phase transitions and random walks on graphs: a generalization of the Mermin–Wagner theorem to disordered lattices, fractals, and other discrete structures. Phys. Rev. Lett. 68 (1992).

  124. Reitz, M. & Bianconi, G. The higher-order spectrum of simplicial complexes: a renormalization group approach. J. Phys. A 53 (2020).

  125. Bianconi, G. & Dorogovstev, S. N. The spectral dimension of simplicial complexes: a renormalization group theory. J. Stat. Mech. 2020 (2020).

  126. Nurisso, M. et al. Higher-order Laplacian renormalization. Nat. Phys. (2025).

  127. Cheng, A., Xu, Y., Sun, P. & Tian, Y. A simplex path integral and a simplex renormalization group for high-order interactions. Rep. Prog. Phys. 87 (2024).

  128. Ghavasieh, A., Nicolini, C. & Domenico, M. Statistical physics of complex information dynamics. Phys. Rev. E 102 (2020).

  129. Villegas, P., Gabrielli, A., Santucci, F., Caldarelli, G. & Gili, T. Laplacian paths in complex networks: information core emerges from entropic transitions. Phys. Rev. Res. 4 (2022).

  130. Binney, J. J., Dowrick, N. J., Fisher , A. J. & Newman, M. E. The Theory of Critical Phenomena: An Introduction to the Renormalization Group (Oxford Univ. Press, 1992).

  131. Pathria, R. K. & Beale, P. D. Statistical Mechanics (Elsevier/Academic, 2011).

  132. Holland, P. W., Laskey, K. B. & Leinhardt, S. Stochastic blockmodels: first steps. Soc. Networks 5 (1983).

  133. Burioni, R. & Cassi, D. Universal properties of spectral dimension. Phys. Rev. Lett. 76 (1996).

  134. Moretti, P. & Muñoz, M. A. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun. 4 (2013).

  135. Poggialini, A., Villegas, P., Muñoz, M. A. & Gabrielli, A. Networks with many structural scales: a renormalization group perspective. Phys. Rev. Lett. 134 (2024).

  136. de C. Loures, M., Piovesana, A. A. & Brum, J. A. Laplacian coarse graining in complex networks. Preprint at arXiv (2023).

  137. Garuccio, E., Lalli, M. & Garlaschelli, D. Multiscale network renormalization: scale-invariance without geometry. Phys. Rev. Res. 5 (2023).

  138. Avena, L., Garlaschelli, D., Hazra, R. S. & Lalli, M. Inhomogeneous random graphs with infinite-mean fitness variables. Preprint at arXiv (2022).

  139. Lalli, M. & Garlaschelli, D. Geometry-free renormalization of directed networks: scale-invariance and reciprocity. Preprint at arXiv (2024).

  140. Uchaikin, V. V. & Zolotarev, V. M. Chance and Stability: Stable Distributions and their Applications (Walter de Gruyter, 2011).

  141. Samorodnitsky, G. & Taqqu, M. S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance (Chapman & Hall, 1994).

  142. Lévy, P. L’addition des variables aléatoires définies sur une circonférence. Bull. Soc. Math. Fr. 67 (1939).

  143. Balkema, A. A. & Resnick, S. I. Max-infinite divisibility. J. Appl. Probab. 14 (1977).

  144. Giné, E., Hahn, M. G. & Vatan, P. Max-infinitely divisible and max-stable sample continuous processes. Probab. Theory Relat. Fields 87 (1990).

  145. Verteletskyi, V. Renormalization of Networks with Weighted Links. MSc thesis, Leiden Univ. (2022).

  146. Garlaschelli, D. & Loffredo, M. I. Patterns of link reciprocity in directed networks. Phys. Rev. Lett. 93 (2004).

  147. Garlaschelli, D. & Loffredo, M. I. Multispecies grand-canonical models for networks with reciprocity. Phys. Rev. E 73 (2006).

  148. Squartini, T., Picciolo, F., Ruzzenenti, F. & Garlaschelli, D. Reciprocity of weighted networks. Sci. Rep. 3 (2013).

  149. Gallo, A., Saracco, F., Lambiotte, R., Garlaschelli, D. & Squartini, T. Patterns of link reciprocity in directed, signed networks. Phys. Rev. E 111 (2025).

  150. Ialongo, L. N., Bangma, S., Jansen, F. & Garlaschelli, D. Multi-scale reconstruction of large supply networks. Preprint at arXiv (2024).

  151. Milocco, R., Jansen, F. & Garlaschelli, D. Multi-scale node embeddings for graph modeling and generation. Preprint at arXiv (2024).

  152. Caldarelli, G., Capocci, A., Los Rios, P. & Munoz, M. A. Scale-free networks from varying vertex intrinsic fitness. Phys. Rev. Lett. 89 (2002).

  153. Dehghan-Kooshkghazi, A., Kamiński, B., Kraiński, Ł., Prałat, P. & Théberge, F. Evaluating node embeddings of complex networks. J. Complex Netw. 10 (2022).

  154. van der Hofstad, R. Random Graphs and Complex Networks (Cambridge Univ. Press, 2024).

  155. Hattori, K., Hattori, T. & Watanabe, H. Gaussian field theories on general networks and the spectral dimensions. Prog. Theor. Phys. Suppl. 92 (1987).

  156. Burioni, R. & Cassi, D. Random walks on graphs: ideas, techniques and results. J. Phys. A 38 (2005).

  157. Boettcher, S. & Brunson, C. T. Renormalization group for critical phenomena in complex networks. Front. Physiol. 2 (2011).

  158. Dorogovtsev, S. N. Renormalization group for evolving networks. Phys. Rev. E 67 (2003).

  159. Meshulam, L., Gauthier, J. L., Brody, C. D., Tank, D. W. & Bialek, W. Coarse graining, fixed points, and scaling in a large population of neurons. Phys. Rev. Lett. 123 (2019).

  160. Griffiths, R. B. Nonanalytic behavior above the critical point in a random Ising ferromagnet. Phys. Rev. Lett. 23 (1969).

  161. Munoz, M. A., Juhász, R., Castellano, C. & Ódor, G. Griffiths phases on complex networks. Phys. Rev. Lett. 105 (2010).

  162. Amari, S.-i. Information Geometry and Its Applications (Springer, 2016).

  163. Berman, D. S., Klinger, M. S. & Stapleton, A. G. Bayesian renormalization. Mach. Learn. Sci. Tech. 4 (2023).

  164. Raju, A., Machta, B. B. & Sethna, J. P. Information loss under coarse graining: a geometric approach. Phys. Rev. E 98 (2018).

  165. Machta, B. B., Chachra, R., Transtrum, M. K. & Sethna, J. P. Parameter space compression underlies emergent theories and predictive models. Science 342 (2013).

  166. Har-Shemesh, O., Quax, R., Hoekstra, A. G. & Sloot, P. M. A. Information geometric analysis of phase transitions in complex patterns: the case of the Gray-Scott reaction–diffusion model. J. Stat. Mech. 4 (2016).

  167. Ehrenfest, P. & Ehrenfest, T. Begriffliche Grundlagen der statistischen Auffassung in der Mechanik (Springer, 1907).

  168. Niemeijer, T. & Leeuwen, J. M. J. Wilson theory for spin systems on a triangular lattice. Phys. Rev. Lett. 31 (1973).

  169. Kadanoff, L. P. Variational principles and approximate renormalization group calculations. Phys. Rev. Lett. 34 (1975).

  170. Southern, B. W. Kadanoff’s variational renormalisation group method: the Ising model on the square and triangular lattices. J. Phys. A 11 (1978).

  171. Jan, N. & Glazer, A. Kadanoff’s approximate renormalization group transformation applied to the triangular Ising lattice. Physica A 91 (1978).

  172. Nijs, M. & Knops, H. Variational renormalization method and the Potts model. Physica A 93 (1978).

  173. Castro, C. & Jona-Lasinio, G. On the microscopic foundation of scaling laws. Phys. Lett. A 29 (1969).

  174. Gell-Mann, M. & Low, F. E. Quantum electrodynamics at small distances. Phys. Rev. 95 (1954).

  175. Zinn-Justin, J. Quantum Field Theory and Critical Phenomena (Oxford Univ. Press, 2021).

  176. Amit, D. J. & Martin-Mayor, V. Field Theory, the Renormalization Group and Critical Phenomena (World Scientific, 2005).

  177. Täuber, U. C. Renormalization group: applications in statistical physics. Nucl. Phys. B 228 (2012).

  178. Pelissetto, A. & Vicari, E. Critical phenomena and renormalization-group theory. Phys. Rep. 368 (2002).

  179. Efrati, E., Wang, Z., Kolan, A. & Kadanoff, L. P. Real-space renormalization in statistical mechanics. Rev. Mod. Phys. 86 (2014).

  180. Gefen, Y., Mandelbrot, B. B. & Aharony, A. Critical phenomena on fractal lattices. Phys. Rev. Lett. 45 (1980).

  181. Gefen, Y., Aharony, A., Mandelbrot, B. B. & Kirkpatrick, S. Solvable fractal family, and its possible relation to the backbone at percolation. Phys. Rev. Lett. 47 (1981).

  182. Phani, M. K. & Dhar, D. Real-space renormalisation group: application to directed percolation. J. Phys. C 15 (1982).

  183. Gefen, Y., Aharony, A. & Mandelbrot, B. B. Phase transitions on fractals. I. Quasi-linear lattices. J. Phys. A 16 (1983).

  184. Gefen, Y., Aharony, A., Shapir, Y. & Mandelbrot, B. B. Phase transitions on fractals. II. Sierpinski gaskets. J. Phys. A 17 (1984).

  185. Gefen, Y., Aharony, A. & Mandelbrot, B. B. Phase transitions on fractals. III. Infinitely ramified lattices. J. Phys. A 17 (1984).

  186. Das, D., Dey, S., Jacobsen, J. L. & Dhar, D. Critical behavior of loops and biconnected clusters on fractals of dimension d < 2. J. Phys. A 41 (2008).

  187. Della Morte, M. & Sannino, F. Renormalization group approach to pandemics as a time-dependent SIR model. Front. Phys. (2021).

  188. Cavagna, A. Dynamic scaling in natural swarms. Nat. Phys. 13 (2017).

  189. Cavagna, A. Dynamical renormalization group approach to the collective behavior of swarms. Phys. Rev. Lett. (2019).

  190. Cavagna, A. Natural swarms in 3.99 dimensions. Nat. Phys. 19 (2023).

  191. Koch-Janusz, M. & Ringel, Z. Mutual information, neural networks and the renormalization group. Nat. Phys. 14 (2018).

  192. Li, S.-H. & Wang, L. Neural network renormalization group. Phys. Rev. Lett. (2018).

  193. Hu, H.-Y., Li, S.-H., Wang, L. & You, Y.-Z. Machine learning holographic mapping by neural network renormalization group. Phys. Rev. Res. 2 (2020).

  194. Caso, F., Trappolini, G., Bacciu, A., Liò, P. & Silvestri, F. Renormalized graph neural networks. Preprint at arXiv (2023).

  195. Young, A. P. & Stinchcombe, R. B. A renormalization group theory for percolation problems. J. Phys. C 8 (1975).

  196. Reynolds, P. J., Stanley, H. E. & Klein, W. A real-space renormalization group for site and bond percolation. J. Phys. C 10 (1977).

  197. Galam, S. Real space renormalization group and totalitarian paradox of majority rule voting. Physica A 285 (2000).

  198. Kogan, O., Rogers, J. L., Cross, M. C. & Refael, G. Renormalization group approach to oscillator synchronization. Phys. Rev. E 80 (2009).

  199. Östborn, P. Renormalization of oscillator lattices with disorder. Phys. Rev. E 79 (2009).

  200. Garlaschelli, D., Hollander, F., Meylahn, J. & Zeegers, B. Synchronization of phase oscillators on the hierarchical lattice. J. Stat. Phys. 174 (2019).

  201. Levin, M. & Nave, C. P. Tensor renormalization group approach to two-dimensional classical lattice models. Phys. Rev. Lett. (2007).

  202. Evenbly, G. & Vidal, G. Tensor network renormalization. Phys. Rev. Lett. (2015).

  203. Bal, M., Mariën, M., Haegeman, J. & Verstraete, F. Renormalization group flows of Hamiltonians using tensor networks. Phys. Rev. Lett. (2017).

  204. Lenggenhager, P. M., Gökmen, D. E., Ringel, Z., Huber, S. D. & Koch-Janusz, M. Optimal renormalization group transformation from information theory. Phys. Rev. X 10 (2020).

  205. Gökmen, D. E., Ringel, Z., Huber, S. D. & Koch-Janusz, M. Statistical physics through the lens of real-space mutual information. Phys. Rev. Lett. 127 (2021).

  206. Gordon, A., Banerjee, A., Koch-Janusz, M. & Ringel, Z. Relevance in the renormalization group and in information theory. Phys. Rev. Lett. 126 (2021).

  207. Sarra, L., Aiello, A. & Marquardt, F. Renormalized mutual information for artificial scientific discovery. Phys. Rev. Lett. 126 (2021).

  208. Gökmen, D. E., Ringel, Z., Huber, S. D. & Koch-Janusz, M. Symmetries and phase diagrams with real-space mutual information neural estimation. Phys. Rev. E 104 (2021).

  209. Canet, L., Delamotte, B., Deloubrière, O. & Wschebor, N. Nonperturbative renormalization-group study of reaction–diffusion processes. Phys. Rev. Lett. 92 (2004).

  210. Canet, L., Chaté, H. & Delamotte, B. Quantitative phase diagrams of branching and annihilating random walks. Phys. Rev. Lett. 92 (2004).

  211. Canet, L., Chaté, H., Delamotte, B., Dornic, I. & Muñoz, M. A. Nonperturbative fixed point in a nonequilibrium phase transition. Phys. Rev. Lett. 95 (2005).

  212. Canet, L., Chaté, H. & Delamotte, B. General framework of the non-perturbative renormalization group for non-equilibrium steady states. J. Phys. A 44 (2011).

  213. Tarpin, M., Benitez, F., Canet, L. & Wschebor, N. Nonperturbative renormalization group for the diffusive epidemic process. Phys. Rev. E 96 (2017).


参考文献可上下滑动查看


复杂网络动力学读书会


集智俱乐部联合合肥工业大学物理系教授李明、同济大学副教授张毅超、北京师范大学特聘副研究员史贵元与在读博士生邱仲普、张章共同发起「复杂网络动力学」读书会。本次读书会将探讨：同步相变的临界性、如何普适地刻画多稳态与临界点、如何识别并预测临界转变、如何通过局部干预来调控系统保持或回到期望稳态、爆炸逾渗临界行为的关键特征、不同类型的级联过程对逾渗相变的影响有何异同、高阶相互作用的影响能否等效为若干简单机制的叠加、如何有效地促进人类个体间的合作等问题。读书会已完结，现在报名可加入社群并解锁回放视频权限。

详情请见：复杂网络上的自组织与集体行为：从扩散、相变到博弈 | 读书会启动


推荐阅读
1. Nature Physics评论：重整化群50年，应用于非平衡系统前景广阔
2. 重整化遇见机器学习：多尺度视角探索复杂系统内在的统一性
3. Nature Physics：重整化群——理解异构网络的显微镜
4. 游戏化科研——让我们突破内卷、共研涌现
5.  探索者计划 | 集智俱乐部2025内容团队招募（全职&兼职）

6. 加入集智，玩转复杂，共创斑图！集智俱乐部线下志愿者招募



点击“阅读原文”，报名读书会