AI科学家做研究：他们的观点会一致吗？
摘要
当两个 AI 模型在同一科学任务上训练时，它们学到的是相同的理论，还是两种不同的理论？纵观科学史，我们见证了理论在实验验证或证伪驱动下的兴衰：在实验数据匮乏时，可能会并存多种理论，但随着更多实验数据的出现，可存续的理论空间将愈发受限。近日，集智社区科学家，来自MIT Max Tegmark团队的刘子鸣等研究者发现，同样的故事也发生在 AI 科学家身上：随着训练数据中系统数量的不断增加，AI 科学家所学理论趋于收敛，尽管有时它们会形成对应不同理论的不同群体。为了机械化地揭示 AI 科学家所学理论并量化它们的一致性，我们提出了 MASS——作为 AI 科学家的哈密顿-拉格朗日（Hamiltonian-Lagrangian）神经网络，在物理学的标准问题上进行训练，并汇总多个随机种子下的训练结果，以模拟不同配置的 AI 科学家。我们的主要发现包括：当在经典力学教科书问题上训练时，AI 科学家偏好完整的哈密顿（Hamiltonian）或拉格朗日（Lagrangian）描述；当扩展到非标准物理问题时，拉格朗日描述具有良好的泛化性，这表明拉格朗日动力学在丰富的理论空间中仍然是唯一准确的描述。我们还观察到训练动态和最终学习权重对随机种子高度依赖，正是这种“种子依赖”控制了相关理论的兴衰。除了可解释性之外，MASS 还统一并超越了拉格朗日神经网络和哈密顿神经网络，为动力系统学习提供了全新的工具。
关键词：AI科学家（MASS）；理论收敛（Theory Convergence）；哈密顿描述（Hamiltonian）；拉格朗日描述（Lagrangian）；可解释性（Interpretability）；多物理系统训练（Multi-physics Training）
彭晨丨作者
论文题目：Do Two AI Scientists Agree?
论文链接：https://arxiv.org/abs/2504.02822
发表时间：2025年4月3日
探究AI科学家的理论演化
探究AI科学家的理论演化
自人类历史以来，从阿基米德的浮力原理到牛顿的经典力学，再到爱因斯坦的相对论，科学家们不断在实验数据的推动下修正与完善理论框架。如今，随着深度学习与大语言模型（LLMs）的崛起，计算机不仅能辅助分析，还逐渐具备从原始数据中发现物理规律的能力。论文由此提出一个核心问题：当不同的AI模型（“AI科学家”）在同一科学任务上独立训练时，它们究竟会收敛到同一套理论，还是各自演化出不同的“学说”？研究者选取经典与合成的一维物理系统，构建可同时学习哈密顿与拉格朗日理论的MASS框架，开展一系列受控实验，力图揭示AI科学家在理论空间中的“生存与竞争”法则。
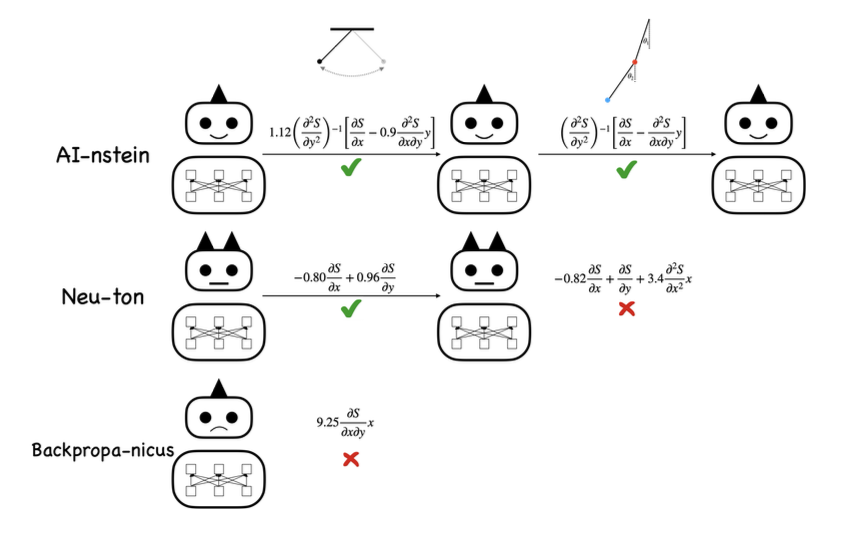
图1. 人工智能科学家的进化。不同的人工智能科学家从同一物理系统的数据中学习，即使是在简单的钟摆实验中，也会得出不同的结果。不能支撑当前实验数据的理论被标记为错误的。幸存的人工智能科学家面临着更复杂的系统，比如双摆。人工智能科学家修改他们的理论来模拟新的数据。最终，剩下的人工智能科学家会学到什么？
MASS：架构设计与核心理念
MASS：架构设计与核心理念
过去的工作多聚焦符号回归或遗传编程（symbolic regression, genetic programming）方法，以较强先验假设束缚搜索空间，或直接在模型架构中硬编码哈密顿（Hamiltonian Neural Network）或拉格朗日（Lagrangian Neural Network）动力学方程。与之不同，MASS在最小物理先验下解放理论表达自由度，通过学习一阶与二阶导数及其组合项，让网络自主筛选出最有效的理论成分。此种策略不仅能揭示多个等价理论的共存态，也为探索未知系统提供了更宽广的理论空间。
MASS的核心在于首先将多个物理系统（如简谐振子、单摆、开普勒问题等）的轨迹数据同时输入网络，通过共享的自动微分层计算出对坐标与速度的各阶导数，形成数百种“原子级”候选函数项（如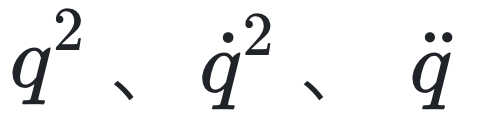 
等）。然后，MASS 在多阶段增量训练中依次加入不同系统的数据，通过线性读出层为每个候选项学习权重，并借助稀疏正则化剔除大部分无关项，只保留那些能在所有系统上同时解释观测的关键成分。这样，随着新系统的不断加入，仅有最通用、最简洁的理论表达（完整的哈密顿或拉格朗日形式）得以幸存；而对不同随机初始化的模型进行对比，又可以量化“AI 科学家”之间对同一任务的理论一致性与多样性。
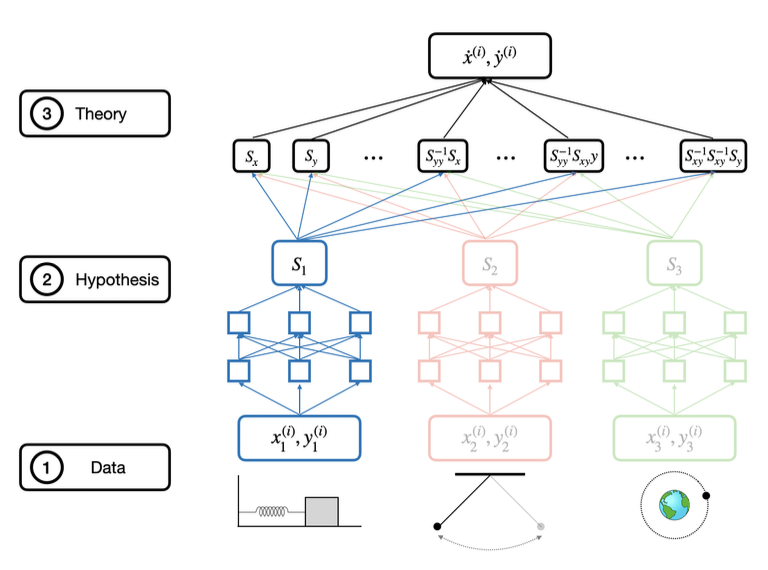
图 2. MASS架构。
实验与结果：多维度实验剖析
实验与结果：多维度实验剖析
方法：多系统统一理论求解
在具体实现中，研究团队选取包括简谐振子、单摆、开普勒问题及相对论振子等四个经典系统，以及两个人工合成势能（α、β系统），构成共七个一维问题。在每一阶段，MASS接收新系统数据，累积训练误差并更新模型权重，以模拟AI科学家在不断获取新观测时的理论修正过程。训练策略采用AdamW优化器，结合余弦学习率调度与正则化手段，确保导数矩阵的数值稳定性与模型的可解释性。
多系统实验结果
-
单系统实验：当MASS仅接触简谐振子时，模型迅速收敛到低均方误差，并在最终线性层中筛选出数十个显著权重项。尽管理论项远多于传统
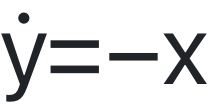的简单表达，但通过分析激活相关性可发现这些项高度聚类，实质上对应同一哈密顿或拉格朗日描述的不同代数等价形式。
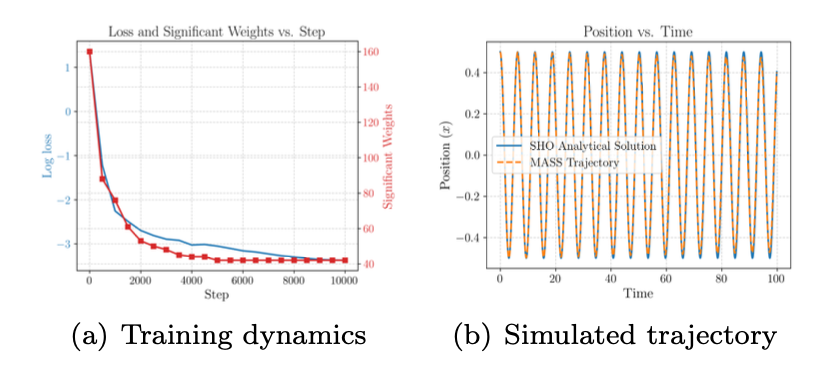
图 3. 单个简谐振子上质量的训练结果。(a) MASS（种子0）训练到在每一步批次大小为512的10000步中MSE损失。显著权值的数量，计算为最后一层占总范数前99%的权值的数量，随着损失而减少。(b)单个振荡器的重建运动准确地捕获了运动的频率和幅度。
-
多系统挑战：随着单摆、引力势和相对论势等系统依次加入训练，存活下来的显著项数量明显减少，表明只有更简洁的理论能在多重物理约束下通行无阻。同时，不同随机种子初始化的MASS网络在某些阶段会“淘汰”原有理论，转而学习更通用的表达，从而体现了“优胜劣汰”的训练动力学。
图 4. MASS在更复杂的系统上训练。虚线表示训练的不同阶段。从简谐振子开始，系统分别在第10000步、第20000步、第30000步应用于单摆、引力势和相对论谐振子。损失累加在MASS在训练的每一步所接触的所有系统上。
-
拉格朗日vs哈密顿形式：在添加更复杂或合成势能后，MASS从最初偏好哈密顿形式（Hamiltonian，T+V）逐渐转向拉格朗日形式（Lagrangian，T−V），并在线性拟合中表现出与手工推导的拉格朗日激活项极高的相关性（R²>0.9）。这一现象不仅印证了拉格朗日描述在广义坐标系下的普适性，也提示AI模型在多系统通用场景下的理论偏好。
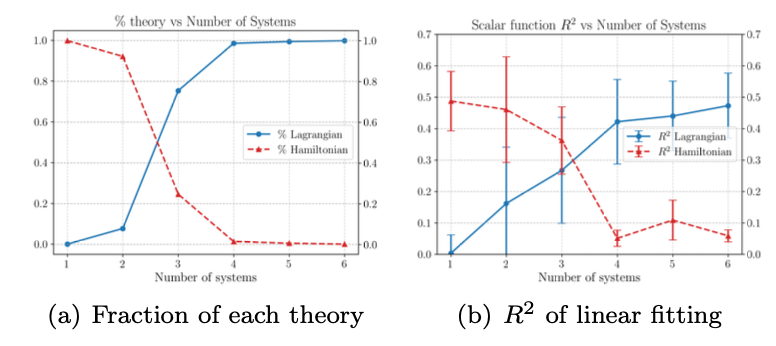
图 5. MASS从学习哈密顿理论切换到学习拉格朗日理论。(a)知道c1和c2是相反符号（拉格朗日符号）和相同符号（哈密顿符号）的MASS科学家的比例。(b)激活值与拉格朗日势与哈密顿势的线性拟合的R2分数。误差条表示R2评分的标准差。
-
高维扩展：研究进一步将MASS应用于双摆（double pendulum）等二维混沌系统，并使用四阶龙格－库塔积分复现轨迹。尽管未显式强加能量守恒约束，MASS依然以不足1%的能量漂移成功捕捉到了双摆动力学，彰显其在高维复杂系统中的可扩展潜力。
AI科学家究竟是否达成一致？
AI科学家究竟是否达成一致？
横向比较数十个不同随机种子下的MASS实例，通过主成分分析发现，它们在相同系统上的第一主成分激活高度相关，绝大多数模型最终都选取了同一基础理论。
综合各类实验结果，可以得出结论：不同配置的AI模型在面对相同数据时，会在大部分条件下学习出高度一致的物理理论。虽然在训练过程中会出现阶段性分歧，但随着系统复杂度与数据量的增加，“正确”理论得以在“物竞天择”中胜出，印证了模型在理论空间中向最通用、最简洁描述的收敛趋势。
未来展望
未来展望
论文最后提出数项可行的后续研究方向，包括允许模型学习坐标变换以打破广义坐标限制，将“哈密顿性度量”纳入损失函数以引导不同理论偏好，以及探索更高维度、多体相互作用等更具挑战性的物理体系。
MASS架构不仅为我们揭示了AI科学家们在理论学习上的“群像”，也证明了拉格朗日描述在丰富物理空间中的至关地位。未来，随着计算能力与数据规模的持续攀升，AI或将真正成为不逊于人类的科学发现者，引领我们踏上新的认知高峰。
讲座推荐
本文作者刘子鸣和其导师Max Tegmark都在集智做过精彩报告，这里推荐刘子鸣关于AI驱动的物理规律发现的相关讲座，你也可以在集智斑图平台检索更多相关内容。
大模型可解释性读书会
集智俱乐部联合上海交通大学副教授张拳石、阿里云大模型可解释性团队负责人沈旭、彩云科技首席科学家肖达、北京师范大学硕士生杨明哲和浙江大学博士生姚云志共同发起「大模型可解释性」读书会。本读书会旨在突破大模型“黑箱”困境，尝试从以下四个视角梳理大语言模型可解释性的科学方法论：
自下而上：Transformer circuit 为什么有效？
自上而下：神经网络的精细决策逻辑和性能根因是否可以被严谨、清晰地解释清楚？
7. 探索者计划 | 集智俱乐部2025内容团队招募（全职&兼职）
微信扫一扫,分享到朋友圈
