重整化群与非线性物理，寻找复杂系统跨尺度的分析方法丨新课发布

导语

你知道吗？费根保姆常数可以由重整化群计算，相变临界点可以由重整化方法得出，深度神经网络的多层计算就是在对图像做重整化。重整化群是考察不同尺度下物理规律变化的数学工具，帮助我们理解系统在大范围内或临界点附近的行为。集智学园联合北京邮电大学兰岳恒教授开设「重整化群分析在非线性物理中的应用」系列课程，系统讲述重整化群这一理论框架，怎样用来分析高维非线性系统的性质，实现方程的求解与约化。

本系列课程将回答如下问题：

从有限的观测提取一般性规律建模的原则和常见框架是什么？
怎样写出系统重要结构和运动模式的近似解析表达式？
怎样将对称性、不变性、基本范式等先验知识放到系统解析描述中？
怎样建立系统不同层级动力学间联系的方程？

欢迎感兴趣的研究者加入课程，现在加入可享早鸟价格。

引入

在复杂系统研究中，有许多重要的基本问题，例如如何研究非线性系统的动力学特征、重要结构和运动模式，以及如何研究跨尺度问题等，我们都需要有一套系统的分析方法。

在2024年12月-2025年1月，我们邀请了北京邮电大学兰岳恒教授开设了《Koopman分析在非线性动力学中的应用》系列课程，详细讲解了分析非线性系统动力学的一套方法——Koopman算符，如何将一个非线性问题转化为无穷维函数空间中的线性问题，并应用于非线性动力学、符号动力学、Kuramoto 模型、哈密顿动力学以及气候动力学等不同科目或系统。

时隔半年，我们再次邀请兰岳恒教授开设《重整化群分析在非线性物理中的应用》系列课程，来系统讲解重整群（renormalization group，简称RG）理论，这个在跨尺度问题研究中行之有效的系统分析方法。

重整化群

从原子到生命到浩瀚宇宙，从生物学到物理学中许多现象涉及广阔的尺度。在理论物理中，重整化群是一个考察不同尺度下考察物理规律变化的数学工具，它和“标度不变性”和“共形不变性”关系紧密，都与自相似有关。在传统的重整化理论中，系统在某一个标度上自相似于一个更小的标度，但描述它们组成的参量和变量均不相同，需要“重整”。系统的组成可以是原子、基本粒子、自旋等，系统的变量演化通过系统组成之间的相互作用来描述。

最初，重整化是一种数学技术用来处理物理学中出现的“无穷大”问题。举个例子，在观察电子时，如果从远处看，它的电荷是有限的，因为电子被一个“虚拟正电荷云”包裹着。但如果靠近电子，这种正电荷云的屏蔽效应会逐渐减弱，最终暴露出电子的更大电荷。重整化的关键在于，它通过数学手段将这种无穷大“隐藏”起来，并将实验测量到的有限电荷作为理论的有效值。这个过程虽然看似是“障眼法”，但它的正确性后来得到了更深层次的物理解释。

1954年，物理学家默里·盖尔曼和弗朗西斯·洛首次将重整化与“尺度”联系起来，提出了“有效电荷”的概念：电子的电荷并不是固定的，而是随着观察尺度的变化而变化。这一发现表明，重整化不仅仅是处理无穷大的数学技巧，更是一种描述自然界如何在不同尺度上运行的物理语言。在1971年，盖尔曼的学生肯·威尔逊第一次描述的“重整化群”，将微观与宏观的联系系统化。

重整化揭示了自然界的一个深刻规律：不同尺度上的物理现象可以相对独立，仅仅通过参数来联系。换句话说，研究宏观现象时，我们可以忽略微观层面的复杂细节，微观的影响体现在宏观理论的参数值上；而研究微观现象时，也无需考虑宏观的所有状态，宏观的影响体现在微观个体的环境变量上。这种“尺度分离”的思想成为现代物理学的核心理念之一。

重整化群中的关键思想

重整化操作是在一个更大的长度尺度上对微观自由度做平均，为了保持关心的物理性质不变，参数需要从精细尺度到粗糙尺度做相应的变换，从而形成一种参数（变量）变换的群结构-重整化群。反复应用这种粗粒化过程会产生所谓的参数流。这个流具有不动点，也就是在重整化下保持不变的特殊值。这些参数对应于该系统遵循的普适标度律的临界点，具有相同标度律的系统被认为属于同一个普适类。

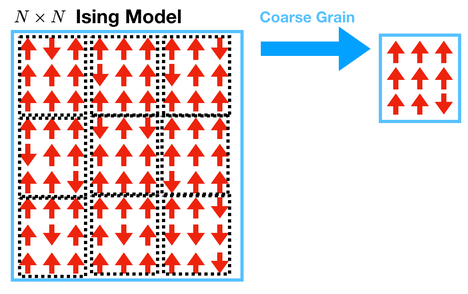
粗粒化示意图：以Ising模型为例

重整化群产生的参数流示意图

重整化群理论中的另一个关键思想是临界维数的存在。超过这个维数，与平均场理论相对应的不动点是稳定的，这意味着它正确地捕捉到了临界行为。对于较低的维度，可以通过微扰求解重整化群方程来得到阶的标度指数，从而找到临界行为的近似值。

重整化群让我们能够专注于不同尺度上的关键变量，而忽略不重要的细节。这种“简化”能力是科学研究得以推进的重要原因。重整化群理论在快速发展中，正在与机器学习、复杂网络、非线性物理等不同领域结合。

本系列课程《重整化群分析在非线性物理中的应用》主要回答如何设计重整化策略来分析高维非线性系统的性质，实现方程的求解与约化，为分析计算复杂系统中的跨尺度问题提供有力工具。

课程主题：

重整化群分析在非线性物理中的应用

课程简介

从有限的观测提取一般性规律建模的原则和常见框架是什么？
怎样写出系统重要结构和运动模式的近似解析表达式？
怎样将对称性、不变性、基本范式等先验知识放到系统解析描述中？
怎样建立系统不同层级动力学间联系的方程？

这些都是复杂系统研究需要考虑的基本问题，重整化群分析能够提供一套行之有效的系统分析方法。

复杂系统研究已经成为各学科需要共同面对的问题。其多自由度、高非线性、非平衡特性决定了多层次结构和自组织动力学的涌现，体现对外部激励呈现复杂的适应性。怎样从基本原理发掘特定系统的基本特性，理解其行为和设计合适的调控方案，是信息智能时代人们关注的核心问题之一。本次课程计划系统讲述重整化群这一理论框架，怎样用来分析高维非线性系统的性质，实现方程的求解与约化。

重整化群方法始于场论，在凝聚态相变中进一步发展，用于处理体系中出现的各种奇异性。经Widom，Kadanoff和Wilson等人的拓展，成为了联系不同尺度下物理规律的有力工具。在复杂系统研究中，更是可以帮助我们进行状态粗粒化并导出粗粒化后的方程；也可以用来解析或数值计算非线性动力系统中重要的轨道。考虑到重整化群也是统计物理中的重要方法，结合此处在动力学分析中的应用，它已经成为联接动力学和统计方法的桥梁和有力工具。

本讲座中，从复杂系统建模的方式出发，讲述对称性、不变性与变换群的关系，强调群结构的重要性，以及重整变换与常用数学物理方法的联系。有了充分准备后，我们将系统阐述重整化群在非线性动力学中的应用：怎样用它来约化方程；怎样用来搜寻重要轨道，包括周期轨道或连接轨道；怎样与Koopman算符本征函数连接。我们希望，此方法可以拓展到真实的复杂系统研究中去。

课程大纲

课程主讲人

兰岳恒，北京邮电大学物理科学与技术学院教授，博士学位在佐治亚理工学院（Georgia Institute of Technology）获得。先后在国内外多个著名大学学习和工作过，有丰富的学科交叉研究经历。主要从事非线性科学、统计物理、生物物理、复杂信息和智能系统等方面的研究工作，注重基本理论方法的发展和与实验紧密结合的应用。现为北京邮电大学“数学与信息网络”教育部重点实验室副主任，多次被邀请在国内外学术会议上报告自己的工作，同时担任期刊“理论物理通信”（Communications in Theoretical Physics）和“现代数学物理”（Modern Mathematical Physics）的编委，也是多个国际著名杂志的审稿人。发表学术论文100余篇，包括国际顶级杂志PRL， PNAS， Nature子刊论文多篇。

课程详情

第一课：复杂系统及其建模

复杂系统都是高维非线性体系，具有层级结构和涌现动力学，能够学习和适应环境变化。研究复杂系统，首先要熟悉其定量描述方式以及各种刻画方式的优势和不足。动力学描述沿袭了经典物理中的力学分析，精确但方程难解；统计物理处理相互作用的多体体系，在简单物理系统中取得了巨大成功，但在非平衡体系中碰到了巨大困难；网络科学则是两者的综合、平衡和拓展，有着巨大生命力，但远远没有达到完美。我们的理论究竟要解决什么问题，怎样解决，需要具备哪些特征？如何直面现实世界的复杂性来建立合适的模型？这里我们抛砖引玉，希望能引起各位的思考与共鸣。

复杂系统及其特征
动力学系统与相空间
统计物理思想
网络科学的兴起

第二课：对称性、不变结构与变换群

对称性与守恒律是现代物理中的重要概念，贯穿于物理研究中的各个领域。除了常见的三种连续对称性之外，我们强调尺度不变性及其相关的Pai定理，这是传统重整化群运作的基石。在非线性动力学中对称性也极其重要，连续对称能够降低系统维度获得解析解，离散对称能够帮助我们约简计算、判断特殊轨道的存在。这样我们就过渡到对称性和不变性的一般描述——群论。这里主要强调群的封闭性，以及同构、同态的概念，可以与复杂系统信息的整合、分解、变换和约化联系起来。

物理中的对称性与守恒律
非线性动力学中的不变性与对称性
群论初步

第三课：重整化初步

理论模型都是对真实物理世界的简化描述，重整的技术实际上在建模中随处可见。这里我们举几个常见的模型重整与约化的例子。更加系统地，物理中的平均场方法实际上就是一个常见但并不平凡的例子；而解微分方程中的常数变异法联系了重整与坐标变换。统计物理中自旋模型重整化，则是重整化群萌芽的经典模型，包含了诸多重要概念。我们也会指出其中比较隐蔽的假设，厘清重整化群和相变的关系，指出重整化群实际上可以推广到一般对称操作。

几个常见模型中的重整与约化
平均场带来的约化
常数变异法
自旋模型中的重整化

第四课：非线性动力学的重整化群分析

重整化群思想的核心还是群的概念，用其进行常见的相变研究只是一个广为人知的应用，而在动力学中的应用则是另一个正在成长的领域。在这里，群的应用主要与约化和不变性相联系。所以我们首先讲述与动力学约化紧密相关的子流形的概念，这也是当前研究机器学习原理重点关注的对象。从系统包含参数的近似解中，我们可以得到重整化群方程，它脱胎于近似解，但很多时候成立的范围大大超出，因为它融入了群不变的性质。实际上，重整化群分析在很大程度上囊括了渐进分析的很多分支，量子力学中的WKB近似就是一例。

粗粒化与子流形
重整化群方程
重整化群分析与渐进分析

第五课：重整化群确定非线性体系的重要轨道

一个重要的应用就是确定非线性系统中的重要轨道，获得其近似解析表达式。一个例子就是连接轨道，它能够连接两个不同稳态的状态转移轨道，也可以是分割不同吸引域的边界，还可以是触发复杂行为的起始点。另一个例子就是周期轨道，无论在守恒系统还是在耗散系统中，都起着极其重要的作用。这里，我们可以用统一的方法，基于重整化群方程获得轨道的近似表达式，以及周期对振幅的依赖关系，在很大程度上免去了多尺度分析带来的繁杂计算。即使对非线性很强的系统、在很大的相空间区域，这里的计算都可以很快收敛到正确的值。

连接轨道
周期轨道

第六课：重整化群分析的更多应用

重整化群分析不仅能够计算方程的近似解，也能够得到精确解。即使是较为复杂的多孤子解，也可以方便得到。这里把群的不变性质用到解的形式不变上面，将复杂非线性问题转化为线性问题或低维非线性问题，大大降低了求解难度。将方程约化到状态空间的子流形上，则是RG分析的应有之用。这里举的例子是描述空间延伸系统的非线性偏微分方程，RG分析可以用更少的自由度达到相同的计算精度，大大提高了计算效率。为复杂非线性系统，例如流体计算、等离子体计算等等提供了一个可以期待的手段。当然，RG分析还有很多未明之端，期待各位同仁共同努力，让这一经典工具焕发新的活力。

精确解
无穷维系统子流形上的约化
系列课程总结

课程信息

课程适用对象

1. 理工科领域研究者及高年级学生

a. 对复杂系统、非线性动力学、统计物理、重整化群等方向有兴趣的研究人员、理工科研究生或高年级本科生；

b. 具备基础微积分、线性代数、常微分方程等数学基础，以及一定的计算能力；

c. 有志于多学科交叉、希望将理论工具应用于物理、工程、信息、生命等复杂系统的研究者。

2. 具有探究精神和创新意识的学习者

a. 喜欢提出问题、参与讨论、推导假设并反思复杂系统本质的学生；

b. 对系统建模、行为理解、规律提取和调控设计等实际问题有浓厚兴趣的学者。

学完将收获

复杂系统建模能力：掌握从有限观测提取规律的建模原则，理解复杂系统的高维非线性及自组织动力学特性，学习设计合适模型和调控方案。
重整化群（RG）理论掌握：深入学习RG框架，理解其在相变及非线性动力学中的应用，掌握状态粗粒化和方程约化的方法。
对称性与不变性分析：学会利用对称性、守恒律和变换群降低系统维度，获得解析解或约简计算。
非线性动力学应用：掌握RG方法约化方程及搜索重要轨道（如周期轨道），通过RG方程简化多尺度分析计算。
层级动力学联系：学习建立系统不同层级动力学联系方程，应用粗粒化、子流形概念于实际问题。
计算效率提升：掌握RG分析获取精确解及转化复杂问题的技巧，提升计算效率。
跨学科视野：结合统计物理、动力学系统及网络科学，培养解决复杂问题的综合能力。

报名须知

课程形式：腾讯会议直播，集智学园网站录播。本系列课程不安排免费直播。
课程周期：2025年7月26日-2025年8月30日，每周六14点-16点进行。
课程定价：原价599，早鸟价479，早鸟优惠截止到2025年7月27日中午12点。

扫码付费报名课程课程链接：https://campus.swarma.org/course/5563?from=wechat

付费流程：

扫码付费；
课程页面添加学员登记表，添加助教微信入群；
课程可开发票。

课程奖学金机制

1. 途径一：发布高质量课程笔记

在集智斑图网站（pattern.swarma.org）完成本课程体系下某个方向的总结文章或学习路径。经集智学园助教团队评定认可后，可作为一条贡献。一条贡献奖励200元奖学金，质量优异的内容，会有浮动奖励。可参考：

2. 途径二：招募课程助理1名

付费报名课程后，联系助教微信申请课程助理。经沟通，成为正式课程助理，完成课程助理任务，在课程结束后退全额学费。

重整化群与非线性物理，寻找复杂系统跨尺度的分析方法丨新课发布