导语


复杂网络广泛存在，无论是细胞、人类大脑、社交群体还是互联网，都是相互连接的多体系统，其宏观特性并非简单地由其微观成分直接决定。这类系统不仅要面对内部局部故障的挑战，还要承受来自外部的干扰或扰动。由于它们错综复杂的结构，一旦受到严重破坏，可能会导致整个系统的崩溃。例如，在电力系统中，一个局部超载可能触发一系列的级联失效（cascading failures）；而生态系统的临界慢化（critical slowing downs）可能导致整个系统走向灭绝。近年来，研究者们深入研究了这一普遍现象，将局部和全局性的故障界定为可能改变系统功能的扰动。这篇发表于 Nature Reviews Physics 的最新综述题目为“复杂网络的鲁棒性与韧性”，但从背景信息和展望来看，其很大程度为网络瓦解（Network Dismantling）问题，主要贡献与见解可以分为网络瓦解问题的起源与发展、复杂网络级联失效的动力学、网络瓦解问题未来展望三个方面。

如果你正在探索复杂网络瓦解相关问题，欢迎你加入集智正在举办的「复杂网络瓦解：从结构脆弱性到智能优化前沿」读书会：

图片
扫码报名

研究领域：复杂网络，网络鲁棒性，网络韧性，网络瓦解，渗流相变，级联失效
Oriol Artime，Marco Grassia，Manlio De Domenico，James P. Gleeson等 | 作者
刘志航 | 翻译
余孟君，梁金，祁明泽 | 审校










推荐语

祁明泽


本文题目为“复杂网络的鲁棒性与韧性”，但从背景信息和展望来看，其很大程度为网络瓦解（Network Dismantling）问题，以及与之相关的渗流相变、级联失效等问题的研究综述。细细品读有很大收获的同时，也不禁好奇文章经历了什么样的写作和审稿故事。为便于理解，从网络瓦解的角度重新审视该论文，文章的主要贡献与见解可以分为以下三个方面：

1. 网络瓦解问题的起源与发展：从网络鲁棒性到网络瓦解问题
文章首先介绍了如何利用渗流理论对网络瓦解问题进行理论解析，概括了生成函数方法和消息传递算法的基本原理，以及基于规则的K-核渗流、爆炸渗流等模型，这类研究也常被称为网络鲁棒性（Network Robustness）问题。进一步，文章聚焦网络瓦解（最优渗流）问题，系统梳理了各类中心性算法、启发式算法和机器学习瓦解算法，在各类人工和真实网络中对比分析了其瓦解效果和时间复杂度，并提供了一个成型的Python代码库以供调用。这些工作无疑为网络瓦解研究者节省了大量用于梳理和复现相关算法的时间，也是本文十分重要的贡献。

2. 复杂网络级联失效的动力学：级联失效模型与防止崩溃方法

网络鲁棒性和瓦解问题研究主要关注网络结构连通性（最大连通片）面对不同节点失效的变化，而实际上节点之间的失效经常不是独立的。级联失效刻画网络中节点损伤之间的动力学过程，文章总结了多层相互依存、阈值模型和过载模型三种不同研究方法，其中节点的失效分别通过相互依存关系、集体行为影响和负荷重分配来造成其他节点失效。文章同样给出了防止和应对网络崩溃的已有研究，包括鲁棒性设计、早期预警指标、自适应响应和修复等。由于该部分涉及到节点失效后功能的恢复与重构，因此研究者也常常将其称之为网络韧性（Network Resilience）问题。


3. 网络瓦解问题的未来：从结构性瓦解到功能性瓦解
级联失效的研究总结，也直接支撑了本文在展望中的主要观点：未来的网络瓦解问题在关注连通性之外，更应考虑与网络动力学相关联的功能性瓦解，任务依赖的瓦解策略可能会比只基于特定拓扑标准的策略造成更大的损害。同时，文章也指出，基于网络隐藏几何和先进人工智能技术的方法，在相关方向研究应用中有很大潜力。









图片


论文题目：
Robustness and resilience of complex networks
论文地址：
https://www.nature.com/articles/s42254-023-00676-y



目录

一、引言

二、背景信息

三、与渗流理论的联系

四、最优渗流和网络瓦解

五、级联失效

六、防止和应对网络崩溃

七、展望



论文要点

  • 在生物学、社会学和工程学等领域，复杂系统可以通过交互网络中单元间的信息交换来定义，展现出如异质性、模块化和层级等多样的结构模式。

  • 由于复杂网络的相互连接特性，它们能够将微小的干扰放大至整个系统层面，因此理解它们在面对外部扰动和内部故障时的鲁棒性至关重要。

  • 研究复杂网络的鲁棒性和韧性涉及探讨通常依赖于度值连通性、空间嵌入、相互依赖和耦合动力学等特征的相变现象。

  • 网络科学提供了一系列理论和计算方法来量化系统对扰动的鲁棒性，并提供了基础方法来设计鲁棒性、识别早期预警信号和制定适应性响应。

  • 这些方法在系统生物学、系统神经科学、工程学以及社会和行为科学等多个学科中都有应用。




一、引言 




在生物学、社会学、社会生态学和工程学等广泛领域中，无论是蛋白质、神经元、个体还是物种等单位，都通过复杂的交互网络进行信息交换[1-3]。这些网络所产生的连接模式通常具有异质性和重尾特征，其中少数单元作为枢纽，而多数其他单元连接较少[4-8]。这些特征显现出明显的介观（mesoscale）组织结构，包括模块化[9-13]、层级结构[14-16]、网络的网络（Networks of networks） [17-22]、高阶结构[23-25]以及隐含的几何形态[26-28]。

鉴于复杂网络在自然和人工系统中无处不在，理解它们在何种条件下能够充分发挥功能，以及它们在应对外部扰动和/或内部故障的脆弱性程度，显得至关重要[29]。实际上，复杂网络的互连性质面对干扰可能产生正面或负面影响。复杂网络能够展现出丰富的行为，从简单地承受并消化特定类型的小幅扰动而不引起大尺度影响，到放大微小的初始损害直至扩展至影响整个系统。一个典型的例子是，位于系统单元间信息交换关键节点的局部扰动（如信号传递、电力重新分配等）触发的级联失效[30,31]。值得注意的是，复杂网络的鲁棒性和韧性特征表现为不同类型的相变现象[32,33]。这些相变的性质取决于系统的结构特征（例如它是否空间嵌入、是否与其他系统相互依赖或是多层次的[34-36]）和其动力学特性（如存在集体行为的涌现情况，例如同步、流行病传播或耦合动力学等[37-40]）。

在实际应用中，研究系统在结构和动力学稳定下对扰动的响应至关重要，这类研究可以帮助我们预测系统可能发生的临界相变[41]。例如，理解细胞代谢网络在特定酶反应的激活或抑制下的级联失效和鲁棒性，对于开发特定疗法、药物再利用，乃至于网络和系统医学领域的广泛应用都有重要意义[9,42,43]。类似地，蛋白质-蛋白质相互作用网络对内部错误或外部干扰的鲁棒性，直接关联到细胞功能及其在生命树中的韧性[44]。在人脑中，局部扰动可能与中风[45,46]等病理状况有关。生态和社会生态系统的稳定性及恢复能力[47-51]，依赖于它们对扰动的鲁棒性。在社会系统中，控制流行病爆发与基础社交网络的渗流特性[38]紧密相关，而金融和经济系统中系统性风险的传播[53-56]，依赖于它们对级联失效的韧性，这与电网中导致普遍停电的情况[57,58]类似。从互联网[61,62]到航空路线[63]等交通网络的效率，以及它们对错误和扰动的容忍度，都可以通过渗流分析来理解[59,60]。

尽管这些应用无处不在，且理解导致系统崩溃的条件至关重要，但对相关文献的系统性概述仍然缺失。这篇文章通过回顾当前网络瓦解（network dismantling）的方法，将现有的实证案例研究分为三个部分：设计鲁棒性、预警信号和适应性响应，以填补这一空白。具体而言，我们首先介绍具有操作性的网络鲁棒性和韧性的理论框架。随后，我们探讨了复杂网络与渗流理论之间的联系，并介绍了在最优渗流和网络瓦解领域中使用的理论和计算方法。我们进一步讨论了级联失效，以及导致刻画网络系统性风险传播的相变发生的机理。我们还讨论了防止和应对网络系统崩溃的策略，并指出了未来可能的研究趋势。值得注意的是，尽管本综述主要聚焦于网络节点的移除，但所讨论的大多数概念、度量和技术同样适用于网络连边的移除。




二、背景信息




在这篇综述中，我们研究的系统都具有网络结构特点。网络是由单元（节点）通过边或其他链接方式非平凡地相互连接而成的集合。在物理学文献中，网络也常被描述为由座（sites）和键（bonds）组成。网络可以通过邻接矩阵A在数学上表示，其中任意元素Aij在节点i和j之间存在交互或关系时为正值，否则为零。在微观层面，一个常用的连接度量是节点的度数ki，用于量化与节点i相关联的连边数目，而更复杂的描述符则被用来捕捉各种网络特征，从三角形聚集倾向到单元间信息交换的中心性等[3]。

理解网络的结构和功能如何受到单个元素（节点和/或边）失效的影响，是一项富有挑战性的任务。实际上，微观层面的故障并非线性累积，虽然大部分故障可能不会严重影响底层系统的功能，但去除特定元素可能会导致系统的崩溃。系统转向崩溃的过程越突然，就越难以捕捉预警信号来防止它，或设计有效应对措施来减轻其影响。

我们需要考虑一系列不同的情景，每个情景都有不同的含义。一方面，我们可以假设内部故障是随机分布的，比如由一个节点（例如路由器）或一条边（比如通信通道）故障引起[29]。但由于大多数真实世界网络具有高度异质的连通性[4]，它们通常能够抵抗此类随机故障。另一方面，网络结构可能被代理利用，以通过有针对性的攻击来蓄意破坏系统，如实施免疫策略[64]、打击犯罪网络、虚假信息或恶意软件网络[65,66]，以及对电力和天然气分配系统的恶意攻击等[67,68]。但是，每次攻击都有其固有成本，这取决于特定系统，因为移除一个节点或边对应于一个行动，比如接种疫苗、逮捕或关闭服务器。因此，网络瓦解的目标是通过移除尽可能少的节点和/或边来达到既定目标，从而最小化成本。在数学上，这一过程转化为设计一个移除算法和一个需要相应优化的成本函数。

遗憾的是，即使在小型网络上，找出最优的目标节点或连边也是一项挑战性的任务。一次全面的搜索需要探索所有可能移除的节点和/或边的组合。这个操作随着系统规模呈指数级增长，因为破坏系统所需移除的单元数量并非事先就能知道[69]。比如，在一个只有50个节点的小型网络中，要找到最优的节点集合可能需要测试大约250 ≈ 1015种组合。

因此，这一相应的组合优化问题，即网络瓦解，被归类为NP-难问题（即无法在多项式时间内求得最优解）。为了解决这一问题，通常采用多种不同的方法，包括应用近似理论模型和计算启发式算法。

此外，在文献中对于如何衡量系统健康状况或确定网络瓦解的目标，即攻击的具体目的，尚无普遍共识。换句话说，我们应该如何量化迄今为止对系统造成的损害，以便停止攻击？在网络瓦解过程中，又应优化哪些功能呢？在损害衡量方面，最常见的方法是应用与渗流相关的指标，如监控最大连通片（largest connected component ，LCC）的大小，并在其达到预定目标大小时停止攻击[70]。此外，也有研究利用其他网络指标，如网络效率[59,71]或嵌套性[50,51,72]。然而，对于网络瓦解过程后连通片的理想大小，也并无共识。实际上，表征系统失效的大小（无论是相对还是绝对大小）很大程度上取决于系统本身及其应用场景[4,66,68,69,73]。在优化目标方面，不同的研究有不同的焦点，有些旨在寻找可能的最小节点集合[29,69]，有些则致力于在攻击开始后尽可能减小LCC的大小[68]，还有些则关注于降低网络瓦解的成本[66]，因为某些节点的移除可能比其他节点更具成本。这些目标并不总是相容的，且目标的选择还取决于特定应用和攻击期间可用的资源，如时间或资金。

另一个需要考虑的问题是攻击算法本身的计算成本，这可以通过算法的运行时间和内存使用量来衡量。计算复杂度（或时间复杂度）[74]提供了一种衡量算法解决问题所需时间的方法，因此可以用来严格比较不同算法的效率。具体来说，主要假设是算法的运行时间与其执行的基本操作数量成正比，这些操作数量以输入大小的函数形式表达，并且假设所有类型的操作所需时间相同。尽管这个假设并非完全准确，但它是衡量随着输入大小增加所需时间如何变化的良好近似，并且不受硬件、软件或编程语言配置的具体影响——理论上，每个算法至少可以构建一个优化配置。特别是，常用于比较的大O符号[74]，表示作为输入大小的函数时执行的操作数量的渐近值，并除非另有明确说明，通常指的是最坏情况。实际上，最优情况通常与简单的实例相关，因此并不重要，而平均情况则通常难以计算，因为它取决于特定的输入和算法路径。例如，时间复杂度为O(N)表示给定输入大小N时，算法执行N次操作，而O(N2)表示执行N2次操作。对空间复杂度的考量也类似，它衡量内存使用量如何随输入大小变化。然而，值得注意的是，由于空间复杂度通常不是算法的限制因素，所以文献中通常不考虑空间复杂度。

在接下来的部分，我们将探讨前述理论问题与渗流理论之间的直接联系。渗流理论是统计物理中广泛应用的框架，用于研究系统的行为及其对扰动的临界反应。




三、与渗流理论的联系




渗流理论无疑是处理网络瓦解问题最直接和最直观的框架，因此也是被研究得最多的。这个著名模型最初在凝胶研究中理论上被提出[75]，后来在统计物理[32,76]和概率论[77]领域进一步发展，并在科学和工程的各个领域得到广泛应用[78-80]。渗流可以视为一种实验，在此实验中，根据一些预定义的规则（也称为攻击策略，attacking protocols）移除节点和/或连边，然后计算剩余网络的不同统计和几何属性（见图1a）。这种方法允许我们在系统组分因某种原因（如故障、维持、攻击等）失效时，追踪系统的结构响应。这些组件的状态被视为二元的：存在（功能正常）或移除（已失效），通常会计算由功能正常节点形成的剩余连通片的大小。渗流理论与网络瓦解之间的富有成效的联系源自于这样一个假设：一个系统要正常运行，无论其功能如何，必须全局连通。因此，网络退化导致的功能损失可以映射到渗流模型的相变过程。在操作上，这通常通过诸如临界点和最大连通片（LCC，在热力学极限下也被称为巨组分（giant component））的大小来方便地表征，从而提供对网络瓦解过程的定量和定性洞察（见图1b-d）。

图1 渗流作为网络鲁棒性的静态方法。a、由于根据预定义的移除协议Φ选择了一些节点（灰色节点），网络解体。干预的结果是网络分裂成三个连通片，它们的大小分别为S1、S2和S3。这些簇大小是渗流研究中的一个核心量。b-d、Φ的性质与控制参数相关，严重影响网络的响应，导致最大连通片大小的不同类型的相变。e、具有均匀和异质连接模式的网络（粗略地说，度分布的二阶矩与平均值的平方相当或远大于平均值）对故障和有针对性的攻击的响应方式。圆圈代表连通分量，其半径取决于其节点数量。每个垂直列假设删除相同数量的节点或链接。e部分改编自参考文献[225]。


在复杂网络中，节点在结构或功能上并不如规则晶格（Regular Lattices）中的节点那样同质。存在大量的方法和度量标准，可以根据不同的标准对节点进行排序，这些通常是由具体应用驱动的。这种内在的异质性提供了多种攻击策略的选择，从而使我们能够在许多与物理学相关的场景下评估网络的鲁棒性。例如，随机选择节点的方法被用来模拟系统中发生的故障和错误，而更精细化的针对性攻击则可以作为有信息的干预措施来执行。这种干预可能基于拓扑信息，例如移除具有最多连边或最大中心性的节点[81,82]，或者基于非拓扑信息，例如根据节点或连边的元数据来进行干预[83]。

网络瓦解策略与网络拓扑之间的交互是非平凡的。无论是在人工网络还是在实证网络中，同质或异质的连接模式都可能引发截然不同的反应[29]（见图1e）。由于同质网络中最大可能的节点度数与平均值相近，它们对故障和攻击的反应相似，总能找到一个有限瓦解点（见图1e）。然而，对于异质网络，如无标度网络，由于枢纽节点的作用，故障和攻击会导致不同的响应。当故障随机发生时，枢纽节点非常有效地维持着网络的连通性，但如果节点作为目标被直接攻击，则网络会迅速分裂——这就是异质网络所特有的“鲁棒而脆弱” （robust-yet-fragile）的特性（见图1e）。同质网络和异质网络之间的这种差异与非相关网络中瓦解点的预测一致[84,85]；并且已经通过基于生成函数（generating functions）的理论方法得到了更系统和定量的描述。

依赖生成函数的方法优势在于其数学上的灵活性，能够包含更广泛的情况，同时对临界指数提供一定的预测力[85,90,91]，或者对临界点和最大连通片大小提供封闭形式的公式（Closed-form equations）[92]。这些方法假设底层网络是配置模型（configurational model）的退火版本，因此在系综级别处理网络鲁棒性，并有助于揭示度分布pk或其参数所起的作用。例如，给定一个节点移除协议Φk与度数相关，那么最大连通片的大小SGF由以下方程求解得出：


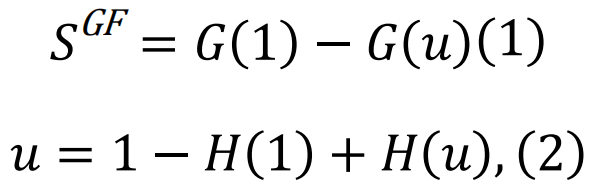
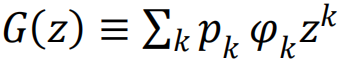其中，和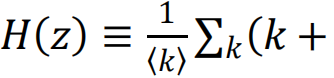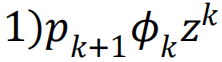是度分布和剩余度分布的生成函数。（超额度（excess degree）是一个节点随机选择的邻居的连接数减一。）〈k〉表示平均度。网络瓦解点由相应的方程给出。类似的方程也可以用于随机连边故障的情形[93]。通过这些方程，我们可以轻易验证在座渗流（移除节点）和键渗流（移除链接）中，瓦解点的位置是一致的。值得注意的是，只要网络中的连接模式不是特别异质，刻画相变的临界指数也是一致的，并且它们与网络无关，等同于平均场预测[76]。然而，这些结果不适用于更异质的网络：例如，在无标度网络中，普适性等价性被打破[94]，且临界指数可能依赖于度分布的指数[85]。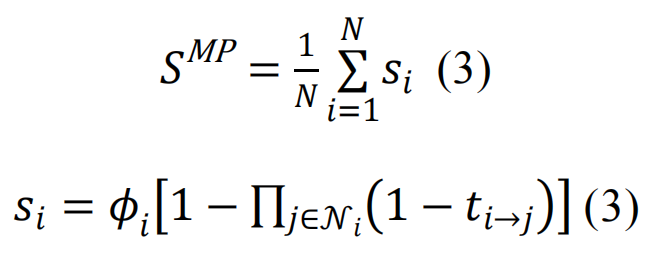

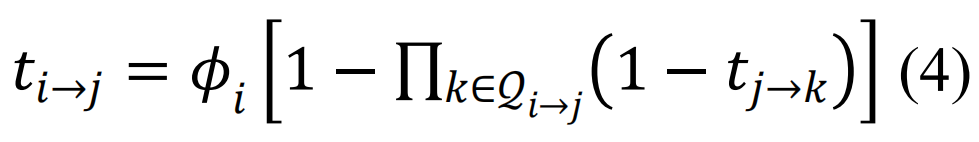
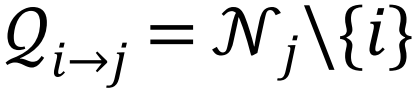针对连边的定向攻击在文献中的探讨相对较少。为了在瓦解过程中编码链接信息，需要同时考虑链接两端节点的拓扑属性，这需要比之前提到的方法更复杂的数学处理[95]。尽管如此，许多实证网络是加权的，或在连边上定义了特征和/或元数据。因此，将瓦解问题在这些情况下公式化，无疑将是渗流理论未来应用的一个富有成果的领域。

生成函数用以精确预测实证网络的鲁棒性方法可能并不总是实用的，因为我们关注的是特定网络拓扑对于故障的响应，而非关注网络的整体。在这种情况下，消息传递方法（message-passing methods）可能更为方便，因为它使用网络的实际连通性而非其度分布作为输入，来计算渗流量[97-100]。这种方法导致了更复杂的数学和数值处理，但通常能提供比基于生成函数方法更好的最大连通片和临界点估计[101,102]。

例如，如果我们用Φi表示节点i未被移除的概率，网络的巨组分SMP的大小由如下公式给出：


在此，Si代表节点i属于巨组分的概率， 表示节点的邻域，节点j通过（有向）消息的形式将属于最大连通片的概率传递给周围节点，代表接受到节点j传递消息的节点子集。通常情况下，是为了避免回溯信息，尽管考虑短程环路的其他选择也是可能的[102]。在接近瓦解点时，所有ti→j的都趋向于0，所以可以扩展方程（5）得到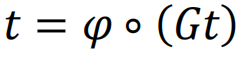，其中∘是Hadamard积， ，每个Φi出现ki次。G是一个维度为2∣E∣ × 2∣E∣ 的逻辑矩阵，其中 ∣E∣ 是连边数，并且它依赖于。瓦解条件由在特征值问题中涌现的非平凡解决定，其中是Hadamard除法，λ是特征值。Perron–Frobenius定理表明，非平凡解与算子G的最大特征值相关。对于常数占用概率φi=φ，可以得到Φc=1/λmax，其中λmax是G的最大特征值。

消息传递方法也可以用于键渗流。如果随机选取的一部分1-φ的连边从网络中移除，则最大连通分量的大小由给SMP/φ出。因此，消息传递对于座渗流和键渗流预测了相同的渗流阈值，这与基于生成函数的预测一致[94]。基于连边攻击的网络瓦解可以在这个框架下轻松实现，因为每个独立连边的移除概率可以编码在一个新的占用概率向量φ’中，然后将其应用于键渗流的消息传递方程。

渗流理论还有助于对呈现出拓扑关联的网络的鲁棒性进行预测，这是大多数实证互连系统的一个特征。其中一种关联被称为同配混合（assortative mixing）[103]，即节点倾向于与相似类型的节点相连。在度数上同配的网络比那些不同配模式的网络更为鲁棒，因为枢纽节点创建了一个在随机攻击或枢纽攻击面前能够维持网络连通性的冗余核心[104]。局部聚类的存在，即相对于随机网络而言封闭三角形的过量，也以不同方式被考虑。根据聚类的定义方式以及其值是高还是低，网络可能被认为比其未聚类的对应系统鲁棒或更不鲁棒[105-108]。超越局部拓扑关联，展示介观非平凡结构的网络的鲁棒性是另一个适合在渗流框架下处理的现象。一种可能的介观尺度结构是核心-外围网络组织[109]。当这些结构随机受到攻击时，它们可能表现出两个瓦解点：一个由核心中的节点引起，另一个由外围中的节点引起[110-112]。另一种结构是k-团，基于渗流的分析有助于识别其重叠社团[113]。

瓦解可能会以一种极难预测的突然方式发生，因为缺乏明显的预警信号。这类突变可能会对社会经济产生巨大影响。最近的例子包括2008年金融危机[114]带来的深远影响，以及COVID-19的传播[115]导致全球经济衰退和生活标准的根本性改变。因此，识别可能出现突然相变的情景具有重要价值。渗流理论提供了多种机制，可以引发这种剧烈的拓扑分裂。其中一种是所谓的k-核渗流，即迭代地移除所有度数小于k的节点[116]。对于k = 2，相变是连续的，但对于k > 2，它变为混合型。自举渗流 (Bootstap percolation) 也可能呈现不连续和混合型相变，它允许被移除的节点在其邻居数量超过一定阈值时恢复[117]。

此外，还有一系列基于特定选择规则的模型，可能会显著加速或延迟达到临界点，尽管这需要依赖于介观层面的信息[118-121]。其中最著名的是导致爆炸渗流（explosive percolation）的乘积规则[122]。乘积规则包括随机均匀选择两条连边，并移除连接的两个组分规模乘积最大的连边：这样，渗流的开始变得突然。此外，瓦解点发生在基于随机连边选择的渗流案例之前。尽管这种相变看起来突然，但已经证明，乘积规则的爆炸性转变实际上是连续的，但具有独特的临界行为[123-125]。关于爆炸渗流的更多信息可以在最近的一篇综述中找到[126]。最后，与不同网络耦合时的互依赖性相关的机制也可能导致突然的瓦解，互依赖性在研究级联失效中起着核心作用，将在下一节中讨论，但它们可以用静态渗流框架进行建模，并揭示出不连续相变出现的条件[127]。

总体而言，由于其灵活性、低计算成本和强大的分析能力，渗流理论在网络鲁棒性研究中占据了核心地位。它提出了根据某些度量来瓦解互连系统的准则，从而揭示了这些精确指标对于系统脆弱性的重要性。然而，在其他情况下，干预准则不依赖于特定度量标准，而是以实现特定目标为导向。基于这一思路，我们在下一节将重点讨论旨在寻找尽可能高效地瓦解网络的策略的算法。




四、最优渗流和网络瓦解




寻找最优策略，即找出实现网络最快瓦解的最小节点集合，是最优渗流问题（Optimal percolation）[128]，也被称为网络瓦解（network dismantling）[69]。这是一个组合优化问题，旨在寻找移除时能最快破坏网络的节点（或连边）集合，使最大连通片分解为孤立的子组件，从而有效降低系统的功能。即便在小型网络上，这样的优化问题在计算上也是具有挑战性的（即，它是NP-hard难题），而且关于瓦解过程后子组件应有的大小，甚至是瓦解的目标在文献中没有统一意见。

早期的工作致力于通过评估节点的一系列拓扑中心性来找到破坏网络的最小节点集。破坏网络的一个简单策略是按照中心性评分的顺序攻击节点。最基本的评分方法是节点的度值，这种方法基于“连接越多越好”的直觉偏好于枢纽节点[29,73]。这些策略也可以分为静态和动态两种，前者在瓦解过程开始时计算节点（或连边）的移除排序，而后者则在过程中更新排序，从而能够适应网络状态的变化。

然而，在某些情况下，关键节点并非连接最多的节点，而是那些连接较少但在网络核心占据战略位置的节点。这些拓扑桥梁体现了社会学中的一个基本概念，即“弱链接的力量”[129]。为了找到这些关键节点，已经提出了许多启发式的中心性度量标准。它们可以大致分为以下几类：基于度值的（如枢纽和k-核）、基于最短路径的（如接近中心性和介数中心性）、基于路径的（如特征向量、特征值和Katz中心性）、基于随机游走的（如PageRank）、基于非回溯游走的，以及基于机器学习的方法。更高层次的分类中，可以区分出真正基于拓扑描述符的结构性方法，和基于节点间某种流动动力学的方法。

最优渗流将寻找最优节点攻击集的搜索过程系统化，试图找到一组节点配置n*，对应于最小的移除比例，使得网络G∞的最大连通分量被最优地瓦解[128]：


最优渗流是一个NP-hard的组合优化问题[130]，由于无法实现G∞(n)的显式函数形式，使得这个问题难以直接解决。然而，对稀疏网络[128]，存在一个近似解方案，从而引出了集体影响力（collective influence, CI）算法[131]。一个近似最优集合可以被视为一系列优化攻击的（无限）序列，这些攻击是对非回溯矩阵最大特征值最小化的连续逼近。这就产生了具有度值ki的节点i的CI指数：


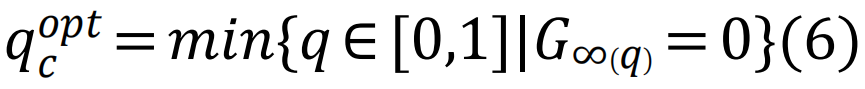
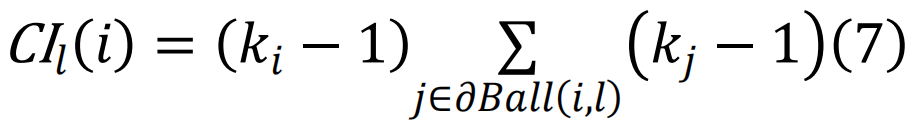
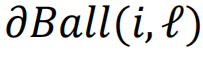其中，表示以节点i为中心、半径为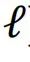（基于最短路径距离估算）的球体表面。这个算法提供了对最优渗流集的良好近似。后来，基于消息传递[132]和置信度传播（belief propagation）[133]的更好算法被提出，包括去环瓦解[69,134]以及爆炸渗流[64]。这些方法严谨地处理了最优渗流问题，增进了我们的理解，并进一步产生了一系列适用于大规模复杂系统复杂而高效的算法。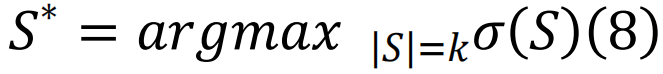

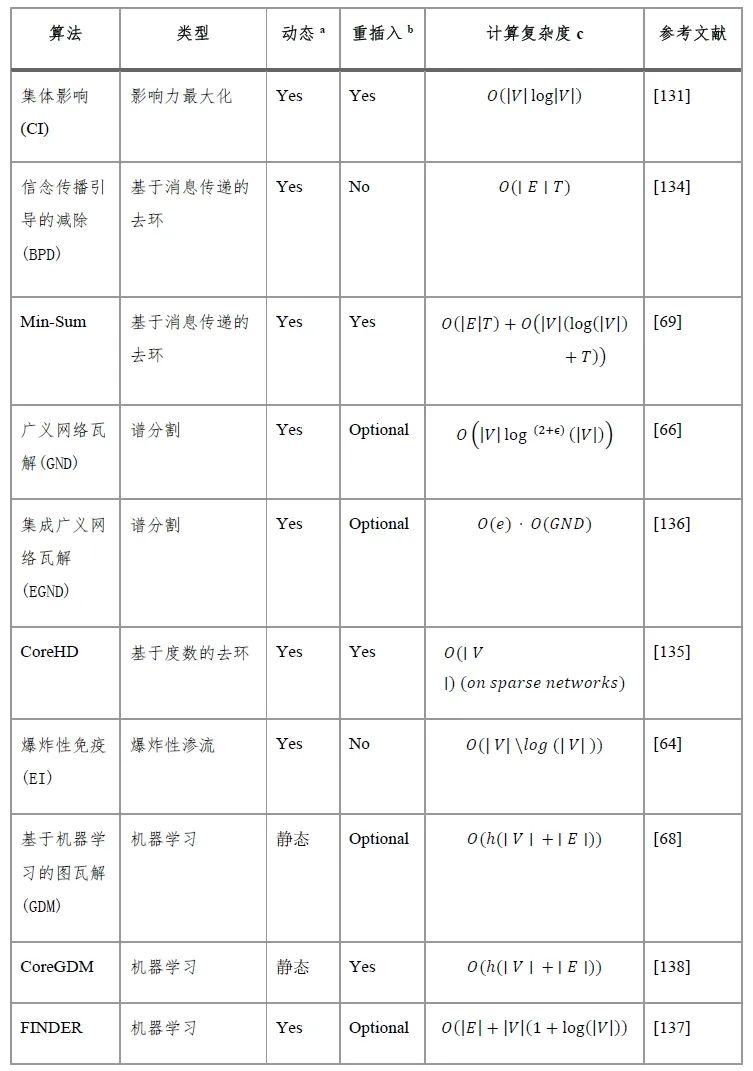
一项研究表明[134]，通过破坏由最小反馈节点集找到的循环（也称为“去环”）可以实现最大连通片的最优瓦解。对于稀疏随机网络，小连通分量中很少存在短环。如果切断最大连通片中的长环，网络将分裂成小的树状片段。最优去环阈值对应最优渗流阈值的上限[69]。最优去环是一个NP-hard问题，可以通过置信度传播算法近似求解。已经开发了两种方法：置信度传播引导的化简算法（the belief propagation-guided decimation algorithm） [134]和Min-Sum算法[69] ，尽管复杂度有所增加，它们找到的影响力节点集合比CI算法更小。特别是，这两种算法首先通过消息传递算法对网络进行去环处理，然后使用树破坏器算法（tree-breaker algorithm）分解所得到的森林（即树的不相交组合）。尽管消息传递迭代的计算复杂度与连边数呈线性关系，但参考文献[69]中提出的贪婪树破坏器算法的复杂度O(N(log(N+T)))随T和N数量级缩放，其中T是森林中树的最大直径，N是节点数。此外，Min-Sum算法还包括攻击结束后的重新插入阶段，即一个贪婪过程，重新插入实际上不需要的节点以达到预期目标。这个重插入阶段旨在减少实际从网络中移除的节点数，从而降低攻击成本，适用于胖尾网络，在这些网络中，去环和瓦解问题并不等同。这一阶段报告为亚线性时间复杂度，但确切的复杂性尚未明确[135]。

受到这些基于去环的算法的启发，研究者们开发了其他算法。CoreHD[135]是一个简单而快速的启发式算法，对于稀疏网络其复杂度为O(N)，其思想是通过迭代从2-核中移除度值最高的节点来实现去环，然后采用与Min-Sum算法相同的树破坏和重插入算法。爆炸性免疫算法[64]基于爆炸渗流相变。广义网络瓦解[66,136]旨在解决非单元的移除成本问题，并基于迭代移除那些能最大化近似谱分割的节点。

其他研究还提出了基于机器学习的攻击策略，如基于机器学习的图瓦解（graph dismantling with machine learning , GDM）[68]和FINDER[137]。这两种方法都利用几何深度学习，具体来说是图神经网络，在小型合成网络上学习攻击策略。然而，GDM是在暴力求解出的网络最优瓦解节点集合数据上进行监督学习，而FINDER采用强化学习方法。另一个算法是CoreGDM[138]，它受到CoreHD的启发，使用GDM模型攻击网络的2-核。此外，还研究了欧几里得空间和双曲空间中网络嵌入的性能[139]。

最优渗流还在多重网络[140]和博弈论[141]上进行了研究。

在网络动力学信息流方面，最优渗流旨在寻找能阻止信息传播的“超级阻断者”的最小集合 [142]。一个相对的问题是找到能在被选为种子时最大化信息传播的超级传播者。一般来说，这两个问题并不一定等价[143]。然而，在一种特定形式的线性阈值传播模型中，阈值由给出，在这种情况下，最优渗流与影响力最大化问题等价[128,130]。影响力最大化问题的目标是找到能在网络中引发最大规模信息传播过程的k个超级传播者（影响者）的最优集合。对于给定数量的初始传播者k，我们希望找到一个具有最大影响力σ(S*) 的k节点集合S*：


这种方法将最优渗流的应用扩展到了各种社会问题和更广泛的领域：影响者理论在多个应用中发挥作用，比如在社交媒体中识别有影响力的传播者、在大流行病中找出超级传播者、识别可能导致疾病的遗传网络中的关键基因突变、确定大脑中对整合至关重要的区域、识别其灭绝可能引发生态系统崩溃的关键物种，以及寻找“大到不能失败”（too big to fail）的金融机构。

为了实现这一目标，研究者提出了一种基于将网络状态编码到适当定义的密度矩阵中的方法[145]。在这种方法中，网络的鲁棒性在与信息通过网络传播所需时间尺度相对应的多个层面上进行分析[146]。对社会、生物和交通系统的实证应用表明，对信息动力学至关重要的节点也负责保持网络的结构完整性，但反之并非必然成立，并且功能性瓦解往往在完全结构性瓦解之前发生[147]。

表1总结了上述算法及其主要特点。在进行鲁棒性评估时，需要针对每个待瓦解的特定网络评估哪种方法在物理意义上最有意义且计算上最高效的。例如，如果将算法应用于腐败网络（见图2），带有重新插入功能的GDM算法是最快瓦解它的，大约在309个节点中仅需移除20个。然而，并不存在适用于所有情况的算法，正如我们在表2中所总结的（完整结果见补充表3）。在此，我们对来自不同应用领域（如生物、信息、社会和技术）的大量实际网络进行了性能比较，发现最优算法在各领域内部和跨领域之间都存在差异。关于所选实证网络的更多详细信息，请参见附表1和2；对于合成网络以及Lancichinetti–Fortunato–Radicchi模型的比较，请参见附表4和5。

表 1 针对性攻击的主要算法汇总

注：V|，节点数量；|E|，边数量；e，集合大小；h，使用的注意力头数量；a 算法是否为动态（或静态）；b 算法是否包含重插入节点的阶段；c 报告针对稀疏网络


图2 最新网络瓦解方法的比较。a, 算法在驱动系统——一个拥有309个节点的巴西腐败网络[65]——走向瓦解方面进行了比较，瓦解程度通过最大连通片的相对大小来衡量。b-g, 展示了部分a中不同曲线的瓦解路径。节点的颜色（从深红到白色）代表攻击顺序（灰色节点未被移除），节点的大小代表它们的介数值。攻击后剩余节点的轮廓颜色代表它们所属的簇。部分a改编自参考文献[68]， MS+R，即Min-Sum算法加上重插入阶段。


表2 真实世界网络瓦解的平均方法下曲线面积（AUC），按类别分组

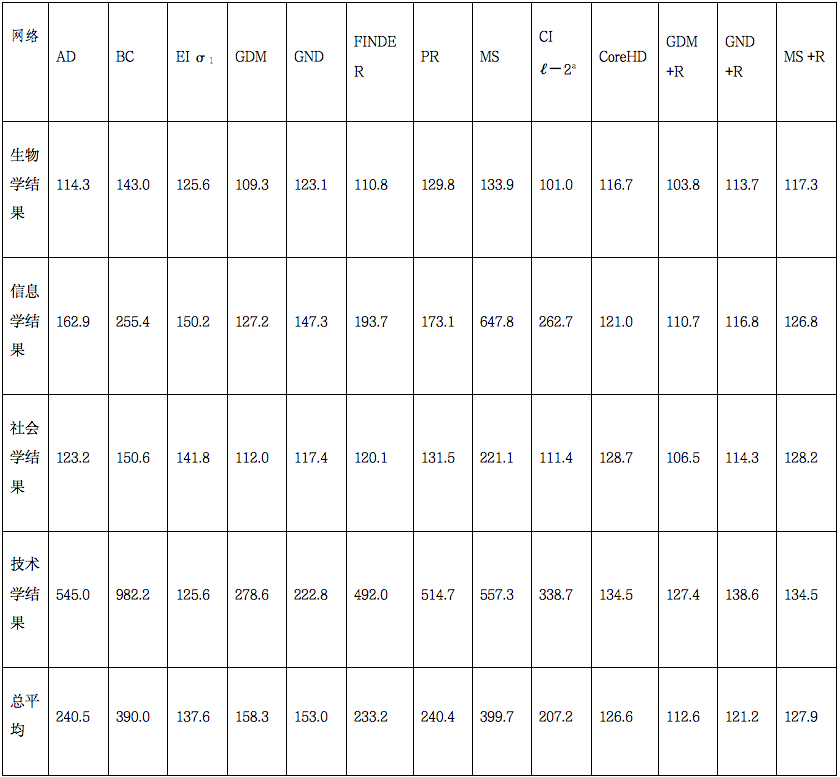
注：每种方法的瓦解目标是网络大小的10%。通过使用辛普森规则对∣LCC(x)∣/∣V∣（最大连通片（LCC）大小作为移除节点的函数）值进行积分计算AUC。为了便于阅读，每个网络的AUC值表示为在该网络上表现最优的方法所得值的百分比，即AUC越低越好。完整结果可在补充表3中查看。AD, 自适应度数；BC, 介数中心性；CI, 集体影响；EI, 爆炸性免疫；GDM, 基于机器学习的图解体；GND, 广义网络瓦解；MS, 最小和；PR, PageRank；+R, 执行了重插入阶段。a CI和CoreHD与其他+R算法进行了比较，因为它们包含了重插入阶段。


除了表1中展示的特设算法外，我们还可以采用直接优化算法（如模拟退火、禁忌搜索或遗传算法）来寻找最优的瓦解集合qc。然而，由于搜索空间维度大，这些算法的扩展性并不好，因此往往无法提供满意的解决方案。举例来说，Min-Sum算法的表现就超过了模拟退火[135]。

至此，我们已经从渗流模型的静态视角出发探讨了鲁棒性和韧性。然而，我们期望能够处理这样一种场景：网络中小规模的故障以随机或有针对性的方式发生，并可能引发全局范围内的效应，即所谓的级联效应。我们将在下一节中深入研究这个问题。




五、级联失效




网络中可能发生的最具破坏力的过程是级联失效。实际系统所遭受的错误和攻击通常具有动力学特性，哪怕它们源自系统的某个小的、局部的区域，也可能进一步扩散，直至整个系统灾难性地崩溃。例如电网中的线路故障（见图3a）、生态区域的大规模灭绝，以及在线社交平台上假新闻或谣言的传播（见图3b）。理解这类故障如何传播及其对网络影响的机制至关重要。尽管这与静态渗流框架存在差异，但我们仍借用了一些来自渗流理论的指标来衡量级联失效的鲁棒性和韧性，比如在级联停止后未出故障网络中最大联通片的大小，或者存活下来的最大联通片瓦解时所达到的临界点。

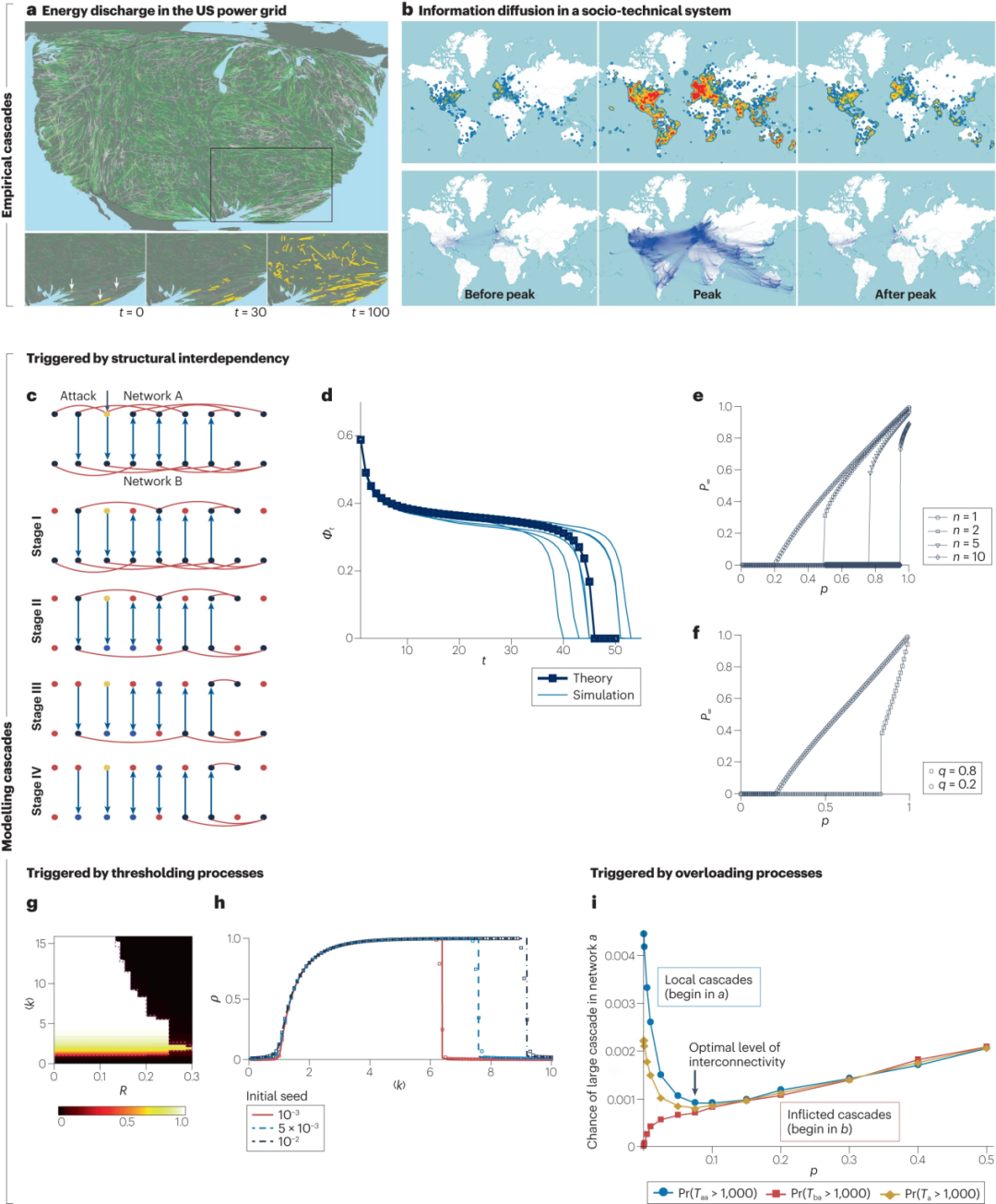
图3 网络失效的演化。a, 在美国-加拿大南部电网的级联传播模拟后的电力线路状态图：未经历停电的线路（绿色）和受影响的电力线路（灰色）。下排：级联由三个故障触发后，受损线路（黄色）演化快照，重缩放时间为t = 0。b, 推特上的信息级联。在诺贝尔奖公告前、期间和之后，有关希格斯玻色子发现的推文密度（上排），以及相应的信息重分享网络（下排）。c, 由相互依赖关系支撑的模型系统中两层耦合网络的故障演变。垂直箭头代表依赖关系。节点颜色表示功能节点（黑色）、最初故障的节点（黄色），以及因不属于最大簇（红色）或依赖于另一个网络中故障节点的单元（蓝色）而被移除。d, 最大连通片的大小（Φt）作为级联步骤（t）的函数。浅蓝线对应于动力学的个体实现，标记表示它们的平均值。深蓝线为理论预测。e,f, 最大连通片的静止大小（P∞）作为最初移除节点比例（p）的函数。实线显示理论预测。n是耦合层的数量；q是双层网络中相互依赖节点的比例。g, 阈值模型中级联停止时的最大连通片，作为阈值R和底层Erdős–Rényi网络的平均度〈k〉的函数。虚线指出级联出现的分析预测。h, 对于固定R = 0.18，级联停止时的最大连通片（ρ）随平均度〈k〉的函数。i, 在两个网络之间的非平凡中间互联水平p（金色曲线，菱形符号）可以缓解大规模负荷削减级联。然而，过多或过少的互连会引发更大的级联，并对鲁棒性产生不利影响。Taa(Tba) 表示在网络a中展开的级联大小，用于在网络a（b）开始的级联。Ta是不区分级联开始位置的网络a中的级联大小。网络a和b各有2,000个节点。部分a经授权转载自参考文献58。部分b改编自参考文献226,。部分c改编自参考文献19。部分d-f转载自参考文献19。部分g,h经授权改编自参考文献171。部分i经授权改编自参考文献190。


在本节中，我们将借助风格化模型来探讨不同的级联失效方式，这些模型旨在提供对故障（或其他事物）传播的普遍洞见。我们从统计物理的视角出发，也就是说，忽略了可能超出本文讨论范围的特定系统的微观、领域导向的特性。相反，我们主张应将注意力集中在大尺度模式和众多看似不同的网络系统中常见的集体涌现行为上。

其中一模型大类是那些通过相互依赖关系传播故障的模型。这是系统理论中的一个核心概念，指的是宏观系统的不同微观和介观部分之间存在的依赖关系，这些关系支持整个系统的正常功能。从生物化学到人造行星工程系统，这些例子遍布许多科学分支[149]。两个等效的理论框架，即多层网络[21,22,150-152]和网络的网络[153,154]，已成功用于构建这类级联的模型。在这些模型中，每一层（或网络）与一个子系统相关联，而依赖关系则通过层间（或网络间）连边编码。与静态渗流不同的是，这种情况涉及到一个逐步退化的网络的快照，其瓦解由依赖相关规则指导（见图3c）。

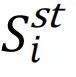2003年，意大利电网因一座电站损坏而发生大停电，导致一些互联网通信网络故障，进而在两个系统间形成了故障的正向反馈循环。这一事件启发了一个理论模型，用于研究双层网络中由相互依赖性引发的级联失效[17]。渗流量，如最大联通片的大小，可以在根据该模型演变的系统的每个快照中进行解析跟踪，与模拟结果非常吻合（见图3d）。该理论灵活且可推广到任意数量的耦合子系统[19,155]、部分和非对称的相互依赖关系[156,157]等。例如，如果层i=1,…,n遭受失效或攻击，导致Φi的功能节点比例下降，而qji表示层i中直接依赖于层j节点的节点比例，那么层中最大连通片的稳态值，可以通过求解以下方程组得到



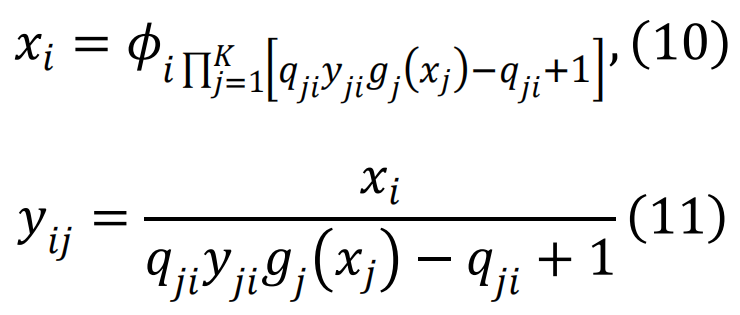
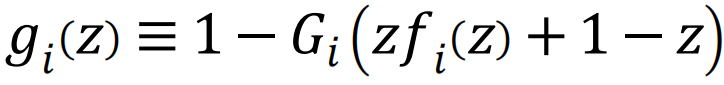其中，，fi(Z)=Hi(Zfi(Z)+1-Z)。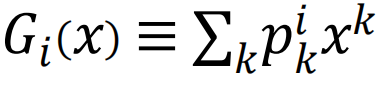是子系统i的度生成函数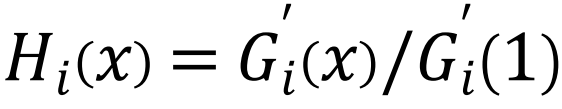，是子系统i的剩余度生成函数，该子系统具有度分布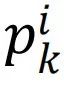。K是通过依赖关系连接到i的层的数量[158]。也可以对由连边故障驱动的级联进行分析处理，但与节点故障传播机制相比研究的较少。

公式（9）至（11）预测了一系列丰富多彩的现象，然而这些现象对相互依赖系统的鲁棒性产生了显著影响。最显著的现象是，随着网络拓扑参数的变化，级联过程结束时最大联通片经历了一个不连续的相变。这种突变导致系统的突然崩溃，而随着完全耦合子系统的数量增加，这种崩溃变得更加难以预测（见图3e）。通过降低层间依赖程度可以减轻这种情况，如果降低得足够多，甚至可以恢复连续的瓦解过程（见图3f）。更重要的是，对公式（9）至（11）的分析提供了如何提高相互依赖耦合系统鲁棒性的见解。目前已识别出三种主要方法：增加自主节点的比例，特别是那些高度数的节点；在相同度数的节点之间设计依赖关系；以及特别注重保护高度值节点不受故障和攻击的影响。在大脑网络的背景下，如果考虑到拓扑相关性，可以提高网络对相互依存引发的级联效应的鲁棒性。我们建议读者参考最近的综述文献[162,163]及其引用文献，以更深入地探讨这类级联类型。

另一类模型起源于集体行为理论，即所谓的阈值模型（threshold model）。在这些模型中，我们假定一个节点的邻居对其状态改变的影响——也就是从正常运作转变为失效——并非随失效邻居数量n线性变化，而是只在超过某个阈值后才会起作用。这类模型通常应用于社会心理学领域，以便理解在什么样的情境下，社会行动者会决定传播谣言、潮流和假新闻，或采取特定行为。这个问题当然与社会层面的网络鲁棒性和韧性密切相关：众所周知，信息的传播可能对公共卫生系统构成严重威胁，极化辩论，甚至破坏公众对民主制度的信任[167,168]。但另一方面，信息传播也可能带来积极影响，例如促进创新等[166,169]。无论如何，这些模型都可以轻松地应用于其他感兴趣领域中发生的级联现象。

在阈值模型中，邻居对节点的影响是非连续的、分段的，这种影响可以通过多种方式实现。一种方法是假设，如果一个节点出现故障邻居比例超过某个特定阈值，那么该节点将会出现故障。这个简单模型导致了一系列丰富的现象，特别是在参数空间中界定的两个相变，一个连续的和一个非连续的（见图3g、h）。实际上，假定初始故障节点数量与系统规模相比小（参见文献[171,172]中关于初始级联播种的作用），并且所有节点的阈值相同（异质阈值也观察到类似现象[170]），那么当阈值较大时，全局级联非常罕见。但是当阈值降低时，网络拓扑开始发挥作用。如果平均度值太小，几乎没有节点能够传播故障，且这些节点彼此孤立；因此，全局级联无法形成。然而，如果平均度值太大，因为大量正常运作的邻居会稳定节点使其始终低于阈值，级联无法发展。下限临界平均度几乎不依赖于阈值，而上限临界平均度则强烈依赖于它。在这两个点之间，容易触发全局级联。全局级联的出现条件及其规模估计已成功推广到具有拓扑关联性的网络、时间和多层网络[173-180]。类似地，人们也采用了更复杂的故障条件，如结合相对和绝对阈值[181]，仅设定绝对阈值[182]，或包括过去故障暴露的记忆[183]。

我们在这部分讨论的最后一组模型是过载模型（overload model）。在这些模型中，节点（或连接）承担着一定的负载 —— 例如电网中的电流、互联网中的数据包、公共交通系统中的乘客，或国际贸易网络中的某种产品（如小麦、大米和玉米）。节点只要将其负荷维持在一个阈值以下——也就是所谓的容量限制——就能正常运作，而这个容量限制理论上可以通过人为干预进行调整。在发生故障或攻击之后，负荷会根据某些规则重新分配，这些规则取决于所要模拟的系统类型，可能导致一系列过载和新的网络内分配事件的链式反应。级联将在所有节点的负荷恢复至其容量以下时结束。

沙堆模型的自组织临界性是最具代表性的负荷重新分配机制之一[184,185]。这些模型的特点是缓慢的外部驱动（例如，通过向系统引入负荷）和非常快速的弛豫过程，在此过程中发生级联（例如，通过过载节点向邻居转移负荷）。弛豫过程被认为极其迅速，以至于在其演化过程中不会增加任何负荷，这通常很好地近似于实证过程，因为级联的展开通常是最快的时间尺度。由于网络中的节点具有不同数量的邻居，将节点容量设置等于其度值成为一种自然选择[186]，尽管还有其他选择可能[187-189]。此外，为了避免网络因负荷过载而饱和，需要在转移负荷时以一定的概率移除部分负荷。在相互依赖的电网背景下已经分析过减负级联模型，在其中发现了一种优化网络耦合水平以减少级联影响的方法[190]（见图3i）。还报告了一些有趣的现象学，例如当自组织临界性规则与Kuramoto模型相结合时，会出现龙王事件（Dragon king events）（即更大级联中的级联）[191]。

还有其他的负荷重新分配机制。一种方法是通过扩展结构与动力学之间的相互作用将负荷与介数中心性（betweenness）关联起来，因为最短路径与交通或路线分配之间存在正相关性[30]。在该模型中，每个节点的容量与其初始介数中心性成正比，当一个节点出现故障时，会发生全局负荷重新分配，可能导致新的节点过载，这些节点并不一定位于先前故障的附近。这种非局域性在空间嵌入网络中容易被直观观察到[35]。对非局域性进行完整、明确的表征仍是一项分析挑战，但已经有不同视角的努力旨在更好地理解其复杂性[192-195]。

具有异构的度分布或者介数中心性分布的网络，如果节点容量不足够大，被发现在面对针对性攻击时极其脆弱[196]。事实上，即使只有一个节点（选择那些介数中心性或度数最大的节点之一）作为初始压力源被破坏，网络也可能崩溃[30]。相反，即使节点的容量很低，无论网络是同质还是异质连接，随机选择一个节点作为初始干扰并不是一种有效的策略来破坏网络。然而，已经在分析上证明，对于足够大的随机选择的节点集合，网络可能遭受一个不连续的瓦解相变[197]。在单层和多层网络中都有报道不连续转变的数值证据[198]。过载模型还在链接故障和干预的背景下进行了研究[199-203]。

到目前为止，我们讨论了静态干预的拓扑影响和有效性，以及局部故障如何在宏观网络部分传播的不同机制。在下一节中，我们将介绍互补视角，即如何以主动和预设的方式防止和应对这些现象。




六、防止和应对网络崩溃




网络崩溃可以通过在其形成阶段应用某些设计原则来预防，这些原则旨在提升网络对随机故障和针对性攻击的韧性[204-208]。然而，这些设计原则并非总是得到应用，或者更糟糕的是，可能被在网络构建时无法预见的高级攻击策略所规避。在这种情况下，即将发生的网络崩溃的早期预警指标[68,209-214]以及对正在发展的崩溃进行的修复和自适应响应[215-217]成为最佳防线。通过促进自发恢复[218,219]或通过微观干预来引发崩溃[215-217,220]，可能可以预防系统性崩溃。这些干预应当采取成本效益高的基于网络的程序[221,222]。

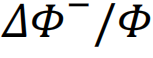网络设计的早期尝试可以追溯到1970年代研究的图增强问题。那时得出的一个成果是，使有向图强连通以及无向图连通或双连通（即移除任一顶点后，图仍保持连通性）所需的最少边数。更近期的网络设计策略则是在2010年代中期提出的[204,205]。特别是对于无标度网络和具有双峰度分布的网络，如果除了一个节点外，所有节点的度数相同，且接近每个节点的平均连接数，同时剩下的一个节点具有非常大的度数k∝N2/3（其中N是构成网络的节点数），那么可以获得最优的鲁棒性[204]。另一种方法基于网络性能的相对下降及其在一系列改进（包括增加或移除特定链接）的情况下的最小化[205]。更具体地说，如果D表示可以对网络G造成的一组可能的损害，是一个映射，给出了损害d∈D之后的新网络，则损害d的重要性由性能的相对下降给出，其中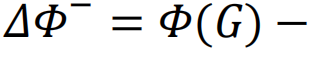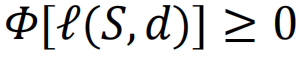。此外，定义临界损害d*∈D为最小化的损害。然后可以将G因D而产生的脆弱性V定义为[205]。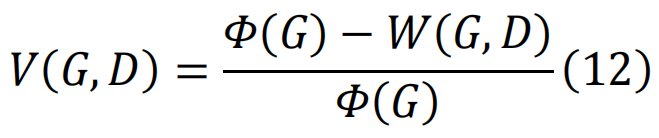


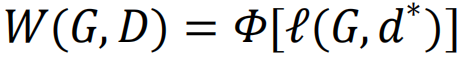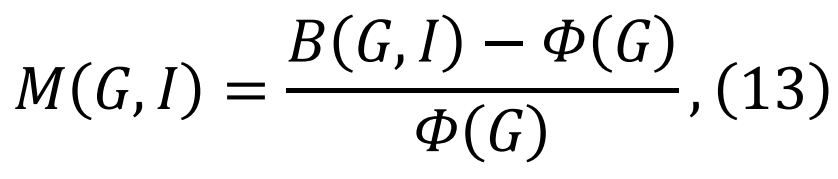
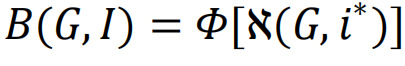其中， 是网络G在损害类别D下的最差性能。同样，我们可以通过映射定义一组改进i∈I，对网络G进行改进，以此实现在临界改进i*条件下网络的最优可提升性。


其中，是在改进类别I下，网络G的最优性能。关于改进i，其重要性由性能相对增加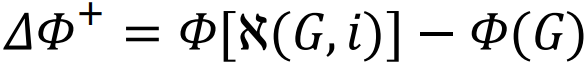给出，其中[205]。然而，对于可优化的内容存在一个基本限制：实际上，网络的鲁棒性和其表现是难以同时最大化的竞争特征[223]。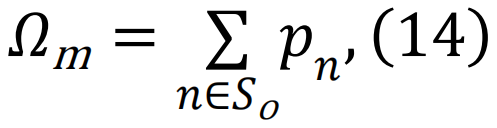

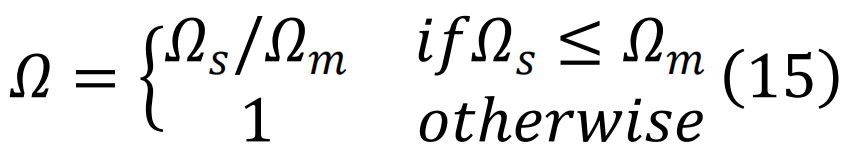
网络设计的概念已进一步扩展至相互依赖的网络体系中[206,162,224]。一个网络系统的稳定性依赖于其内部结构与与其他网络连接模式之间的关系。更具体地说，为了使一个互依赖网络在设计上被认为是鲁棒的，其相互连接应由网络枢纽节点提供，同时网络间的连接应适度集中。如果这两个条件得到满足，那么网络系统可以被认为是稳定的，并且对故障具有鲁棒性。这一结果也已在任务和休息状态下的功能性大脑网络实验中得到证实[206]。

但即使采用了最佳设计实践，网络崩溃有时仍然难以避免。在这种情况下，早期检测至关重要。早期的研究表明，荷兰银行间网络在2008年全球金融危机前夕的许多拓扑属性显示出突然的变化[210]。对于社会生态网络而言，网络协方差矩阵的最大元素被用作预警指标的基础，有效地标示了网络不稳定性[211]。在耦合的人类-环境系统中也有类似的概念被提出，尽管它不是基于网络的范式（formalism），而是基于临界点理论[214]，将临界点理论与网络结构模式结合起来，可以发展出作为早期预警信号的临界减速指标，用于检测结构复杂的生态群落接近潜在临界点的情况[212]。此方法在79个实证互惠网络中成功应用，有效识别出监测社区临近崩溃的关键物种。

近期的研究表明，一台经过训练的机器能够识别高阶拓扑模式，从而有效地解构大规模的社会、基础设施和技术网络[68]，其效率甚至超过了人类的启发式策略。值得注意的是，这个底层程序还可以进行反向工程 —— 机器可以评估未来攻击带来系统解体的概率 —— 从而开发出网络崩溃的预警信号。更具体地说，如果S0是导致网络渗流的虚拟移除节点集，且符合以下约束


那么，在移除一组通用节点集S后，网络的预警值Ω可以通过以下方式给出：


其中，这里的主要思想是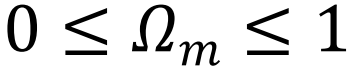，用于量化网络在崩溃前能够容忍的损害程度。当网络的关键节点被移除时，Ω 快速接近 1 [68]（见图 4）。

图4：防止和应对网络崩溃。a, 使用基于度的策略反复攻击三种不同网络基础设施（上排）时，通过Ω测量的早期预警信号，最大连通片（LCC）和第二大连通分片（SLCC）的大小（下排），以及通过机器学习图瓦解（GDM）模型测度移除对系统完整性的重要性（PI）。b–d, 一个动态网络标记（DNM）[227]，它与老鼠肺组织分子网络中基因表达的波动强度（节点颜色）相关，在8小时处存在临界转变（b部分）；DNM已用于捕捉其他系统的早期预警信号，如富营养化湖泊状态（c部分）和美元和欧元货币的利率互换日价格（d部分）。e,f, 规则网络（度连接k = 10，活动点数m = 4，网络规模N = 100）随时间在两种集体模式之间转换的活动节点比例z（上）和系统标记的状态在相图中从t = 0到第一次转变时刻的轨迹（下）。g,h, 一个具有两个网络的系统的最优修复策略，该系统以内部失效节点的比例和为特征。给定一个崩溃系统的初始状态Si，修复相当于最小化Si和绿色区域最近边界之间的距离，在这个区域系统恢复到完全功能状态。箭头表示遵循的轨迹，而R1和R2是三重点。底部展示了两个合成（左）和实证（右）耦合网络的标记编号所示的集体状态。i–k, 重组和重燃：一个两步程序，将一个受干扰的酵母蛋白质相互作用网络从崩溃阶段（红色）驱动到可恢复阶段（蓝色）。图a转载自参考文献68，图b–d转载自参考文献227图e,f转载自参考文献218，图g,h转载自参考文献215，图i–k转载自参考文献217， EUR代表欧洲；L.A.代表洛杉矶；PCC代表皮尔逊相关系数；SD代表标准偏差。


最后，如果鲁棒性设计和早期预警指标未能成功预防网络崩溃，并且网络崩溃已在进行中，则自适应响应和修复成为剩余的两个选项，正如在参考文献215中研究的相互作用金融网络所示。最优控制理论和强化学习已被用于确定最优维护协议，以抵消复杂网络中的老化现象[216]。还开发了一个两步恢复方案，首先进行拓扑重构，其次通过精心施加的微观干预来恢复一个失效的网络[217]（见图4）。

总的来说，本节讨论的方法提供了防止和应对网络崩溃最常用的手段，同时，它们也很可能成为未来在这些方向发展的最肥沃的土壤。





  七、展望




正如本文所述，网络瓦解相关的问题众多，包括理论挑战以及开发能在合理时间内瓦解大型网络的算法的问题。尽管至今我们已经取得了许多成果，但在上述各个方面，仍存在有待进一步研究的开放性问题。

需要深入研究的一方面是结构和功能及其相互影响。现有文献中的大部分瓦解方法都基于攻击，目的是显著降低最大连通片（LCC）的大小。尽管在许多情况下，最大连通片的大小与网络有效运行密切相关，但这并非总是成立。例如，在某些网络上，依赖特定任务的瓦解策略可能会比只基于拓扑标准的策略造成更大的损害。以电网为例，了解电网动力学规则可能会提示出一个更有效的攻击策略：移除对网络稳定性最为关键的节点和/或弧线。在这种情况下，许多已有文献中提到的方法并不适用，因此迫切需要新的理论和计算技术来进行功能性的瓦解网络，并考虑与其上层动力学相关联的各种因素[146,147]。

为实现这个目的，基于复杂网络潜在几何的瓦解方法是一个有潜力的研究方向[28]。尽管基于机器学习的方法已在潜在空间中得到应用，但网络几何与其鲁棒性之间的联系还未深入探讨。这一认识可能推动开发全新类型的算法，用于网络的结构和功能瓦解，同时也有助于提高网络的鲁棒性和韧性。事实上，尽管机器学习等人工智能技术已在诸如自然语言处理、视频和图像处理等领域产生了重大影响，但在网络领域的影响迄今相对有限。然而，这些在技术、算法和硬件理解方面的进步无疑将在众多网络相关任务中发挥作用。

总体而言，理解系统如何对外部冲击做出反应和适应是未来的关键目标。预计统计物理、网络科学和机器学习领域的交叉研究将在此目标中发挥基础作用。潜在应用范围广泛，从细胞层面——需要鲁棒技术来评估基因或药物干预的潜在影响——到流行病学和经济学领域，在这些领域，冲击可能成为系统性问题，从而影响社会的结构和功能。

代码：用于性能比较的代码可以从下述目录中找到
https://github.com/NetworkDismantling/review.



参考文献

  1. Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys.74, 47 (2002).
  2. Newman, M. E. The structure and function of complex networks. SIAM Rev.45, 167–256 (2003).
  3. Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D.-U. Complex networks: structure and dynamics. Phys. Rep.424, 175–308 (2006).
  4. Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science286, 509–512 (1999).
  5. Broido, A. D. & Clauset, A. Scale-free networks are rare. Nat. Commun.10, 1017 (2019).
  6. Gerlach, M. & Altmann, E. G. Testing statistical laws in complex systems. Phys. Rev. Lett.122, 168301 (2019).
  7. Voitalov, I., van der Hoorn, P., van der Hofstad, R. & Krioukov, D. Scale-free networks well done. Phys. Rev. Res.1, 033034 (2019).
  8. Serafino, M. et al. True scale-free networks hidden by finite size effects. Proc. Natl Acad. Sci. USA118, e2013825118 (2021).
  9. Guimera, R. & Nunes Amaral, L. A. Functional cartography of complex metabolic networks. Nature433, 895–900 (2005).
  10. Newman, M. E. Communities, modules and large-scale structure in networks. Nat. Phys.8, 25–31 (2012).
  11. Fortunato, S. & Hric, D. Community detection in networks: a user guide. Phys. Rep.659, 1–44 (2016).
  12. Peixoto, T. P. & Rosvall, M. Modelling sequences and temporal networks with dynamic community structures. Nat. Commun.8, 582 (2017).
  13. Fortunato, S. & Newman, M. E. 20 years of network community detection. Nat. Phys.18, 848–850 (2022).
  14. Ravasz, E. & Barabási, A.-L. Hierarchical organization in complex networks. Phys. Rev. E67, 026112 (2003).
  15. Clauset, A., Moore, C. & Newman, M. E. Hierarchical structure and the prediction of missing links in networks. Nature453, 98–101 (2008).
  16. Peixoto, T. P. Hierarchical block structures and high-resolution model selection in large networks. Phys. Rev. X4, 011047 (2014).
  17. Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature464, 1025–1028 (2010).
  18. Mucha, P. J., Richardson, T., Macon, K., Porter, M. A. & Onnela, J.-P. Community structure in time-dependent, multiscale, and multiplex networks. Science328, 876–878 (2010).
  19. Gao, J., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Networks formed from interdependent networks. Nat. Phys.8, 40–48 (2012).
  20. De Domenico, M. et al. Mathematical formulation of multilayer networks. Phys. Rev. X3, 041022 (2013).
  21. Artime, O. et al. Multilayer Network Science: From Cells to Societies. Elements in Structure and Dynamics of Complex Networks (Cambridge Univ. Press, 2022).
  22. Domenico, M. D. More is different in real-world multilayer networks. Nat. Phys.19, 1247–1262 (2023).
  23. Lambiotte, R., Rosvall, M. & Scholtes, I. From networks to optimal higher-order models of complex systems. Nat. Phys.15, 313–320 (2019).
  24. Battiston, F. et al. The physics of higher-order interactions in complex systems. Nat. Phys.17, 1093–1098 (2021).
  25. Bianconi, G. Higher Order Networks: an Introduction to Simplicial Complexes (Cambridge Univ. Press, 2021).
  26. De Domenico, M. Diffusion geometry unravels the emergence of functional clusters in collective phenomena. Phys. Rev. Lett.118, 168301 (2017).
  27. García-Pérez, G., Boguñá, M. & Serrano, M. Multiscale unfolding of real networks by geometric renormalization. Nat. Phys.14, 583–589 (2018).
  28. Boguna, M. et al. Network geometry. Nat. Rev. Phys.3, 114–135 (2021).
  29. Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature406, 378–382 (2000).
  30. Motter, A. E. & Lai, Y.-C. Cascade-based attacks on complex networks. Phys. Rev. E66, 065102 (2002).
  31. Motter, A. E. Cascade control and defense in complex networks. Phys. Rev. Lett.93, 098701 (2004).
  32. Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. Critical phenomena in complex networks. Rev. Mod. Phys.80, 1275 (2008).
  33. Liu, X. et al. Network resilience. Phys. Rep.971, 1–108 (2022).
  34. Bashan, A., Berezin, Y., Buldyrev, S. V. & Havlin, S. The extreme vulnerability of interdependent spatially embedded networks. Nat. Phys.9, 667–672 (2013).
  35. Zhao, J., Li, D., Sanhedrai, H., Cohen, R. & Havlin, S. Spatio-temporal propagation of cascading overload failures in spatially embedded networks. Nat. Commun.7, 10094 (2016).
  36. Radicchi, F. & Bianconi, G. Redundant interdependencies boost the robustness of multiplex networks. Phys. Rev. X7, 011013 (2017).
  37. Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y. & Zhou, C. Synchronization in complex networks. Phys. Rep.469, 93–153 (2008).
  38. Pastor-Satorras, R., Castellano, C., Van Mieghem, P. & Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys.87, 925 (2015).
  39. De Domenico, M., Granell, C., Porter, M. A. & Arenas, A. The physics of spreading processes in multilayer networks. Nat. Phys.12, 901–906 (2016).
  40. O’Keeffe, K. P., Hong, H. & Strogatz, S. H. Oscillators that sync and swarm. Nat. Commun.8, 1–13 (2017).
  41. Scheffer, M. et al. Anticipating critical transitions. Science338, 344–348 (2012).
  42. Smart, A. G., Amaral, L. A. & Ottino, J. M. Cascading failure and robustness in metabolic networks. Proc. Natl Acad. Sci. USA105, 13223–13228 (2008).
  43. Barabási, A.-L., Gulbahce, N. & Loscalzo, J. Network medicine: a network-based approach to human disease. Nat. Rev. Genet.12, 56–68 (2011).
  44. Zitnik, M., Sosič, R., Feldman, M. W. & Leskovec, J. Evolution of resilience in protein interactomes across the tree of life. Proc. Natl Acad. Sci. USA116, 4426–4433 (2019).
  45. Bullmore, E. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci.10, 186–198 (2009).
  46. Siegel, J. S. et al. Disruptions of network connectivity predict impairment in multiple behavioral domains after stroke. Proc. Natl Acad. Sci. USA113, E4367–E4376 (2016).
  47. May, R. M. Will a large complex system be stable? Nature238, 413–414 (1972).
  48. Holling, C. S. Resilience and stability of ecological systems. Ann. Rev. Ecol. Syst. 1–23 (1973).
  49. Pimm, S. L. The complexity and stability of ecosystems. Nature307, 321–326 (1984).
  50. Pocock, M. J., Evans, D. M. & Memmott, J. The robustness and restoration of a network of ecological networks. Science335, 973–977 (2012).
  51. Bascompte, J. & Stouffer, D. B. The assembly and disassembly of ecological networks. Philos. Trans. R. Soc. Lond. B Biol. Sci.364, 1781–1787 (2009).
  52. Baggio, J. A. et al. Multiplex social ecological network analysis reveals how social changes affect community robustness more than resource depletion. Proc. Natl Acad. Sci. USA113, 13708–13713 (2016).
  53. Gai, P. & Kapadia, S. Contagion in financial networks. Proc. R. Soc. A Math. Phys. Eng. Sci.466, 2401–2423 (2010).
  54. Cimini, G., Squartini, T., Garlaschelli, D. & Gabrielli, A. Systemic risk analysis on reconstructed economic and financial networks. Sci. Rep.5, 15758 (2015).
  55. Bardoscia, M. et al. The physics of financial networks. Nat. Rev. Phys.3, 490–507 (2021).
  56. Grassia, M., Mangioni, G., Schiavo, S. & Traverso, S. Insights into countries’ exposure and vulnerability to food trade shocks from network-based simulations. Sci. Rep.12, 4644 (2022).
  57. Carreras, B. A., Lynch, V. E., Dobson, I. & Newman, D. E. Critical points and transitions in an electric power transmission model for cascading failure blackouts. Chaos12, 985–994 (2002).
  58. Yang, Y., Nishikawa, T. & Motter, A. E. Small vulnerable sets determine large network cascades in power grids. Science358, eaan3184 (2017).
  59. Crucitti, P., Latora, V., Marchiori, M. & Rapisarda, A. Efficiency of scale-free networks: error and attack tolerance. Phys. A Stat. Mech. Appl.320, 622–642 (2003).
  60. Bertagnolli, G., Gallotti, R. & De Domenico, M. Quantifying efficient information exchange in real network flows. Commun. Phys.4, 125 (2021).
  61. Doyle, J. C. et al. The “robust yet fragile” nature of the internet. Proc. Natl Acad. Sci. USA102, 14497–14502 (2005).
  62. De Domenico, M. & Arenas, A. Modeling structure and resilience of the dark network. Phys. Rev. E95, 022313 (2017).
  63. Scott, D. M., Novak, D. C., Aultman-Hall, L. & Guo, F. Network robustness index: a new method for identifying critical links and evaluating the performance of transportation networks. J. Transp. Geogr.14, 215–227 (2006).
  64. Clusella, P., Grassberger, P., Pérez-Reche, F. J. & Politi, A. Immunization and targeted destruction of networks using explosive percolation. Phys. Rev. Lett.117, 208301 (2016).
  65. Ribeiro, H. V., Alves, L. G. A., Martins, A. F., Lenzi, E. K. & Perc, M. The dynamical structure of political corruption networks. J. Complex Netw.6, 989–1003 (2018).
  66. Ren, X.-L., Gleinig, N., Helbing, D. & Antulov-Fantulin, N. Generalized network dismantling. Proc. Natl Acad. Sci. USA116, 6554–6559 (2019).
  67. Matke, C., Medjroubi, W. & Kleinhans, D. SciGRID — an open source reference model for the European Transmission Network (v0.2). http://www.scigrid.de (2016).
  68. Grassia, M., De Domenico, M. & Mangioni, G. Machine learning dismantling and early-warning signals of disintegration in complex systems. Nat. Commun.12, 5190 (2021).
  69. Braunstein, A., Dall’Asta, L., Semerjian, G. & Zdeborová, L. Network dismantling. Proc. Natl Acad. Sci. USA113, 12368–12373 (2016).
  70. Schneider, C. M., Moreira, A. A., Andrade, J. S., Havlin, S. & Herrmann, H. J. Mitigation of malicious attacks on networks. Proc. Natl Acad. Sci. USA108, 3838–3841 (2011).
  71. Kinney, R., Crucitti, P., Albert, R. & Latora, V. Modeling cascading failures in the North American power grid. Eur. Phys. J. B46, 101–107 (2005).
  72. Alves, L. G. et al. The nested structural organization of the worldwide trade multi-layer network. Sci. Rep.9, 2866 (2019).
  73. Cohen, R., Erez, K., Ben-Avraham, D. & Havlin, S. Breakdown of the internet under intentional attack. Phys. Rev. Lett.86, 3682 (2001).
  74. Cormen, T., Leiserson, C., Rivest, R. & Stein, C. Introduction to Algorithms 4th edn (MIT Press, 2022).
  75. Flory, P. J. Molecular size distribution in three dimensional polymers. I. Gelation. J. Am. Chem. Soc.63, 3083–3090 (1941).
  76. Stauffer, D. & Aharony, A. Introduction to Percolation Theory (CRC, 2018).
  77. Broadbent, S. R. & Hammersley, J. M. Percolation processes: I. crystals and mazes. Math. Proc. Camb. Philos. Soc.53, 629–641 (1957).
  78. Isichenko, M. B. Percolation, statistical topography, and transport in random media. Rev. Mod. Phys.64, 961 (1992).
  79. Sahimi, M. Applications of Percolation Theory (CRC, 1994).
  80. Araújo, N., Grassberger, P., Kahng, B., Schrenk, K. & Ziff, R. M. Recent advances and open challenges in percolation. Eur. Phys. J. Spec. Top.223, 2307–2321 (2014).
  81. Rodrigues, F. A. in Network Centrality: an Introduction 177–196 (Springer, 2019).
  82. Holme, P., Kim, B. J., Yoon, C. N. & Han, S. K. Attack vulnerability of complex networks. Phys. Rev. E65, 056109 (2002).
  83. Artime, O. & De Domenico, M. Percolation on feature-enriched interconnected systems. Nat. Commun.12, 2478 (2021).
  84. Molloy, M. & Reed, B. A critical point for random graphs with a given degree sequence. Random Struct. Algor.6, 161–180 (1995).
  85. Cohen, R., Ben-Avraham, D. & Havlin, S. Percolation critical exponents in scale-free networks. Phys. Rev. E66, 036113 (2002).
  86. Gordon, M. Good’s theory of cascade processes applied to the statistics of polymer distributions. Proc. R. S. Lond. A Math. Phys. Sci.268, 240–256 (1962).
  87. Newman, M. E., Strogatz, S. H. & Watts, D. J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E64, 026118 (2001).
  88. Callaway, D. S., Newman, M. E., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: percolation on random graphs. Phys. Rev. Lett.85, 5468 (2000).
  89. Gross, T. & Barth, L. Network robustness revisited. Front. Phys.10, 823564 (2022).
  90. Moore, C. & Newman, M. E. Exact solution of site and bond percolation on small-world networks. Phys. Rev. E62, 7059 (2000).
  91. Goltsev, A. V., Dorogovtsev, S. N. & Mendes, J. F. Percolation on correlated networks. Phys. Rev. E78, 051105 (2008).
  92. Newman, M. Networks (Oxford Univ. Press, 2018).
  93. Li, M. et al. Percolation on complex networks: theory and application. Phys. Rep.907, 1–68 (2021).
  94. Radicchi, F. & Castellano, C. Breaking of the site-bond percolation universality in networks. Nat. Commun.6, 10196 (2015).
  95. Shiraki, Y. & Kabashima, Y. Cavity analysis on the robustness of random networks against targeted attacks: influences of degree-degree correlations. Phys. Rev. E82, 036101 (2010).
  96. Barrat, A., Barthelemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA101, 3747–3752 (2004).
  97. Hamilton, K. E. & Pryadko, L. P. Tight lower bound for percolation threshold on an infinite graph. Phys. Rev. Lett.113, 208701 (2014).
  98. Karrer, B., Newman, M. E. & Zdeborová, L. Percolation on sparse networks. Phys. Rev. Lett.113, 208702 (2014).
  99. Radicchi, F. Percolation in real interdependent networks. Nat. Phys.11, 597–602 (2015).
  100. Newman, M. Message passing methods on complex networks. Proc. R. Soc. A479, 20220774 (2023).
  101. Radicchi, F. Predicting percolation thresholds in networks. Phys. Rev. E91, 010801 (2015).
  102. Radicchi, F. & Castellano, C. Beyond the locally treelike approximation for percolation on real networks. Phys. Rev. E93, 030302 (2016).
  103. Newman, M. E. Assortative mixing in networks. Phys. Rev. Lett.89, 208701 (2002).
  104. Newman, M. E. Mixing patterns in networks. Phys. Rev. E67, 026126 (2003).
  105. Serrano, M. Á. & Boguná, M. Percolation and epidemic thresholds in clustered networks. Phys. Rev. Lett.97, 088701 (2006).
  106. Serrano, M. Á. & Boguná, M. Clustering in complex networks. II. Percolation properties. Phys. Rev. E74, 056115 (2006).
  107. Berchenko, Y., Artzy-Randrup, Y., Teicher, M. & Stone, L. Emergence and size of the giant component in clustered random graphs with a given degree distribution. Phys. Rev. Lett.102, 138701 (2009).
  108. Newman, M. E. Random graphs with clustering. Phys. Rev. Lett.103, 058701 (2009).
  109. Rombach, M. P., Porter, M. A., Fowler, J. H. & Mucha, P. J. Core-periphery structure in networks. SIAM J. Appl. Math.74, 167–190 (2014).
  110. Colomer-de Simón, P. & Boguñá, M. Double percolation phase transition in clustered complex networks. Phys. Rev. X4, 041020 (2014).
  111. Allard, A., Althouse, B. M., Scarpino, S. V. & Hébert-Dufresne, L. Asymmetric percolation drives a double transition in sexual contact networks. Proc. Natl Acad. Sci. USA114, 8969–8973 (2017).
  112. Hébert-Dufresne, L. & Allard, A. Smeared phase transitions in percolation on real complex networks. Phys. Rev. Res.1, 013009 (2019).
  113. Derényi, I., Palla, G. & Vicsek, T. Clique percolation in random networks. Phys. Rev. Lett.94, 160202 (2005).
  114. Claessens, S., Dell’Ariccia, G., Igan, D. & Laeven, L. Cross-country experiences and policy implications from the global financial crisis. Econ. Policy25, 267–293 (2010).
  115. Fernandes, N. Economic Effects of Coronavirus Outbreak (COVID-19) on the World Economy IESE Business School Working Paper No. WP-1240-E (ECGI 2020).
  116. Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. k-core organization of complex networks. Phys. Rev. Lett.96, 040601 (2006).
  117. Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. Bootstrap percolation on complex networks. Phys. Rev. E82, 011103 (2010).
  118. Bohman, T. & Frieze, A. Avoiding a giant component. Random Struct. Algor.19, 75–85 (2001).
  119. Spencer, J. & Wormald, N. Birth control for giants. Combinatorica27, 587–628 (2007).
  120. Beveridge, A., Bohman, T., Frieze, A. & Pikhurko, O. Product rule wins a competitive game. Proc. Am. Math. Soc.135, 3061–3071 (2007).
  121. Krivelevich, M., Lubetzky, E. & Sudakov, B. Hamiltonicity thresholds in Achlioptas processes. Random Struct. Algor.37, 1–24 (2010).
  122. Achlioptas, D., D’Souza, R. M. & Spencer, J. Explosive percolation in random networks. Science323, 1453–1455 (2009).
  123. Riordan, O. & Warnke, L. Explosive percolation is continuous. Science333, 322–324 (2011).
  124. da Costa, R. A., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Explosive percolation transition is actually continuous. Phys. Rev. Lett.105, 255701 (2010).
  125. Grassberger, P., Christensen, C., Bizhani, G., Son, S.-W. & Paczuski, M. Explosive percolation is continuous, but with unusual finite size behavior. Phys. Rev. Lett.106, 225701 (2011).
  126. D’Souza, R. M., Gómez-Gardenes, J., Nagler, J. & Arenas, A. Explosive phenomena in complex networks. Adv. Phys.68, 123–223 (2019).
  127. Son, S.-W., Bizhani, G., Christensen, C., Grassberger, P. & Paczuski, M. Percolation theory on interdependent networks based on epidemic spreading. EPL(Europhys. Lett.)97, 16006 (2012).
  128. Morone, F. & Makse, H. A. Influence maximization in complex networks through optimal percolation. Nature524, 65–68 (2015).
  129. Granovetter, M. S. The strength of weak ties. Am. J. Sociol.78, 1360–1380 (1973).
  130. Kempe, D., Kleinberg, J. & Tardos, É. Maximizing the spread of influence through a social network. In Proc. 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 137–146 (ACM, 2003).
  131. Morone, F., Min, B., Bo, L., Mari, R. & Makse, H. Collective influence algorithm to find influencers via optimal percolation in massively large social media. Sci. Rep.6, 30062 (2016).
  132. Altarelli, F., Braunstein, A., Dall’Asta, L., Wakeling, J. R. & Zecchina, R. Containing epidemic outbreaks by message-passing techniques. Phys. Rev. X4, 021024 (2014).
  133. Altarelli, F., Braunstein, A., Dall’Asta, L. & Zecchina, R. Optimizing spread dynamics on graphs by message passing. J. Stat. Mech. Theory Exp.2013, 09011 (2013).
  134. Mugisha, S. & Zhou, H.-J. Identifying optimal targets of network attack by belief propagation. Phys. Rev. E94, 012305 (2016).
  135. Zdeborová, L., Zhang, P. & Zhou, H.-J. Fast and simple decycling and dismantling of networks. Sci. Rep.https://doi.org/10.1038/srep37954 (2016).
  136. Ren, X.-L. & Antulov-Fantulin, N. in Complex Networks and Their Applications VIII (eds Cherifi, H. et al.) 783–793 (Springer, 2020).
  137. Fan, C., Zeng, L., Sun, Y. & Liu, Y.-Y. Finding key players in complex networks through deep reinforcement learning. Nat. Mach. Intell.2, 317–324 (2020).
  138. Grassia, M. & Mangioni, G. in Complex Networks XIV (eds Teixeira, A. S. et al.) 86–94 (Springer Nature, 2023).
  139. Osat, S., Papadopoulos, F., Teixeira, A. S. & Radicchi, F. Embedding-aided network dismantling. Phys. Rev. Res.5, 013076 (2023).
  140. Osat, S., Faqeeh, A. & Radicchi, F. Optimal percolation on multiplex networks. Nat. Commun.8, 1540 (2017).
  141. Szolnoki, A. & Perc, M. Collective influence in evolutionary social dilemmas. EPL (Europhys. Lett.)113, 58004 (2016).
  142. Chen, B.-L. et al. Influence blocking maximization on networks: models, methods and applications. Phys. Rep.976, 1–54 (2022).
  143. Radicchi, F. & Castellano, C. Fundamental difference between superblockers and superspreaders in networks. Phys. Rev. E95, 012318 (2017).
  144. Makse, H. A. The Science of Influencers and Superspreaders (Springer Nature, 2023).
  145. De Domenico, M. & Biamonte, J. Spectral entropies as information-theoretic tools for complex network comparison. Phys. Rev. X6, 041062 (2016).
  146. Ghavasieh, A., Stella, M., Biamonte, J. & De Domenico, M. Unraveling the effects of multiscale network entanglement on empirical systems. Commun. Phys.4, 129 (2021).
  147. Ghavasieh, A., Bertagnolli, G. & De Domenico, M. Dismantling the information flow in complex interconnected systems. Phys. Rev. Res.5, 013084 (2023).
  148. Lancichinetti, A., Fortunato, S. & Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E78, 046110 (2008).
  149. Strogatz, S. et al. Fifty years of ‘More is different’. Nat. Rev. Phys.4, 508–510 (2022).
  150. Kivelä, M. et al. Multilayer networks. J. Complex Netw.2, 203–271 (2014).
  151. Boccaletti, S. et al. The structure and dynamics of multilayer networks. Phys. Rep.544, 1–122 (2014).
  152. Bianconi, G. Multilayer Networks: Structure and Function (Oxford Univ. Press, 2018).
  153. Kenett, D. Y., Perc, M. & Boccaletti, S. Networks of networks — an introduction. Chaos Solitons Fractals80, 1–6 (2015).
  154. Gao, J., Bashan, A., Shekhtman, L. & Havlin, S. Introduction to Networks of Networks (IOP, 2022).
  155. Gao, J., Buldyrev, S. V., Havlin, S. & Stanley, H. E. Robustness of a network of networks. Phys. Rev. Lett.107, 195701 (2011).
  156. Parshani, R., Buldyrev, S. V. & Havlin, S. Interdependent networks: reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett.105, 048701 (2010).
  157. Schneider, C. M., Yazdani, N., Araújo, N. A., Havlin, S. & Herrmann, H. J. Towards designing robust coupled networks. Sci. Rep.3, 1–7 (2013).
  158. Chen, S., Gao, Y., Liu, X., Gao, J. & Havlin, S. Robustness of interdependent networks based on bond percolation. EPL(Europhys. Lett.)130, 38003 (2020).
  159. Parshani, R., Rozenblat, C., Ietri, D., Ducruet, C. & Havlin, S. Inter-similarity between coupled networks. EPL(Europhys. Lett.)92, 68002 (2011).
  160. Buldyrev, S. V., Shere, N. W. & Cwilich, G. A. Interdependent networks with identical degrees of mutually dependent nodes. Phys. Rev. E83, 016112 (2011).
  161. Reis, S. D. et al. Avoiding catastrophic failure in correlated networks of networks. Nat. Phys.10, 762–767 (2014).
  162. Shekhtman, L. M., Danziger, M. M. & Havlin, S. Recent advances on failure and recovery in networks of networks. Chaos Solitons Fractals90, 28–36 (2016).
  163. Valdez, L. D. et al. Cascading failures in complex networks. J. Complex Netw.8, cnaa013 (2020).
  164. Schelling, T. C. Hockey helmets, concealed weapons, and daylight saving: a study of binary choices with externalities. J. Confl. Resolut.17, 381–428 (1973).
  165. Granovetter, M. Threshold models of collective behavior. Am. J. Sociol.83, 1420–1443 (1978).
  166. Easley, D. & Kleinberg, J. Networks, Crowds, and Markets: Reasoning About a Highly Connected World (Cambridge Univ. Press, 2010).
  167. Gallotti, R., Valle, F., Castaldo, N., Sacco, P. & De Domenico, M. Assessing the risks of ‘infodemics’ in response to COVID-19 epidemics. Nat. Hum. Behav.4, 1285–1293 (2020).
  168. Watts, D. J., Rothschild, D. M. & Mobius, M. Measuring the news and its impact on democracy. Proc. Natl Acad. Sci. USA118, e1912443118 (2021).
  169. Valente, T. W. Network models and methods for studying the diffusion of innovations. Model Methods Soc. Netw. Anal.28, 98–116 (2005).
  170. Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA99, 5766–5771 (2002).
  171. Gleeson, J. P. & Cahalane, D. J. Seed size strongly affects cascades on random networks. Phys. Rev. E75, 056103 (2007).
  172. Liu, R.-R., Wang, W.-X., Lai, Y.-C. & Wang, B.-H. Cascading dynamics on random networks: crossover in phase transition. Phys. Rev. E85, 026110 (2012).
  173. Centola, D., Eguíluz, V. M. & Macy, M. W. Cascade dynamics of complex propagation. Phys. A Stat. Mech. Appl.374, 449–456 (2007).
  174. Gleeson, J. P. Cascades on correlated and modular random networks. Phys. Rev. E77, 046117 (2008).
  175. Dodds, P. S. & Payne, J. L. Analysis of a threshold model of social contagion on degree-correlated networks. Phys. Rev. E79, 066115 (2009).
  176. Hackett, A., Melnik, S. & Gleeson, J. P. Cascades on a class of clustered random networks. Phys. Rev. E83, 056107 (2011).
  177. Snyder, J., Cai, W. & D’Souza, R. M. Degree-targeted cascades in modular, degree-heterogeneous networks. Phys. Rev. Res.4, 013040 (2022).
  178. Karimi, F. & Holme, P. Threshold model of cascades in empirical temporal networks. Phys. A Stat. Mech. Appl.392, 3476–3483 (2013).
  179. Backlund, V.-P., Saramäki, J. & Pan, R. K. Effects of temporal correlations on cascades: threshold models on temporal networks. Phys. Rev. E89, 062815 (2014).
  180. Brummitt, C. D., Lee, K.-M. & Goh, K.-I. Multiplexity-facilitated cascades in networks. Phys. Rev. E85, 045102 (2012).
  181. Yu, Y. et al. System crash as dynamics of complex networks. Proc. Natl Acad. Sci. USA113, 11726–11731 (2016).
  182. Galstyan, A. & Cohen, P. Cascading dynamics in modular networks. Phys. Rev. E75, 036109 (2007).
  183. Dodds, P. S. & Watts, D. J. Universal behavior in a generalized model of contagion. Phys. Rev. Lett.92, 218701 (2004).
  184. Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation of the 1/f noise. Phys. Rev. Lett.59, 381 (1987).
  185. Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality. Phys. Rev. A38, 364 (1988).
  186. Bonabeau, E. Sandpile dynamics on random graphs. J. Phys. Soc. Japan64, 327–328 (1995).
  187. Lise, S. & Paczuski, M. Nonconservative earthquake model of self-organized criticality on a random graph. Phys. Rev. Lett.88, 228301 (2002).
  188. Goh, K.-I., Lee, D.-S., Kahng, B. & Kim, D. Sandpile on scale-free networks. Phys. Rev. Lett.91, 148701 (2003).
  189. Lee, D.-S., Goh, K.-I., Kahng, B. & Kim, D. Sandpile avalanche dynamics on scale-free networks. Phys. A Stat. Mech. Appl.338, 84–91 (2004).
  190. Brummitt, C. D., D’Souza, R. M. & Leicht, E. A. Suppressing cascades of load in interdependent networks. Proc. Natl Acad. Sci. USA109, E680–E689 (2012).
  191. Mikaberidze, G. & D’Souza, R. M. Sandpile cascades on oscillator networks: the BTW model meets Kuramoto. Chaos32, 053121 (2022).
  192. Daqing, L., Yinan, J., Rui, K. & Havlin, S. Spatial correlation analysis of cascading failures: congestions and blackouts. Sci. Rep.4, 5381 (2014).
  193. Hines, P. D., Dobson, I. & Rezaei, P. Cascading power outages propagate locally in an influence graph that is not the actual grid topology. IEEE Trans. Power Syst.32, 958–967 (2016).
  194. Schäfer, B., Witthaut, D., Timme, M. & Latora, V. Dynamically induced cascading failures in power grids. Nat. Commun.9, 1975 (2018).
  195. Valente, A., De Domenico, M. & Artime, O. Non-Markovian random walks characterize network robustness to nonlocal cascades. Phys. Rev. E105, 044126 (2022).
  196. Barthelemy, M. Betweenness centrality in large complex networks. Eur. Phys. J. B38, 163–168 (2004).
  197. Kornbluth, Y. et al. Network overload due to massive attacks. Phys. Rev. E97, 052309 (2018).
  198. Artime, O. & De Domenico, M. Abrupt transition due to non-local cascade propagation in multiplex systems. New J. Phys.22, 093035 (2020).
  199. Moreno, Y., Pastor-Satorras, R., Vázquez, A. & Vespignani, A. Critical load and congestion instabilities in scale-free networks. EPL(Europhys. Lett.)62, 292 (2003).
  200. Lai, Y.-C., Motter, A. E. & Nishikawa, T. Attacks and cascades in complex networks. Complex Netw.650, 299–310 (2004).
  201. Wang, W.-X. & Chen, G. Universal robustness characteristic of weighted networks against cascading failure. Phys. Rev. E77, 026101 (2008).
  202. Cao, X.-B., Hong, C., Du, W.-B. & Zhang, J. Improving the network robustness against cascading failures by adding links. Chaos Solitons Fractals57, 35–40 (2013).
  203. Pahwa, S., Scoglio, C. & Scala, A. Abruptness of cascade failures in power grids. Sci. Rep.4, 3694 (2014).
  204. Paul, G., Tanizawa, T., Havlin, S. & Stanley, H. E. Optimization of robustness of complex networks. Eur. Phys. J. B38, 187–191 (2004).
  205. Latora, V. & Marchiori, M. Vulnerability and protection of infrastructure networks. Phys. Rev. E71, 015103 (2005).
  206. Reis, S. D. S. et al. Avoiding catastrophic failure in correlated networks of networks. Nat. Phys.10, 762–767 (2014).
  207. Carchiolo, V., Grassia, M., Longheu, A., Malgeri, M. & Mangioni, G. Network robustness improvement via long-range links. Comput. Soc. Netw.6, 12 (2019).
  208. Carchiolo, V., Grassia, M., Longheu, A., Malgeri, M. & Mangioni, G. in Internet and Distributed Computing Systems (eds Xiang, Y. et al.) 270–277 (Springer, 2018).
  209. Chen, L., Liu, R., Liu, Z.-P., Li, M. & Aihara, K. Detecting early-warning signals for sudden deterioration of complex diseases by dynamical network biomarkers. Sci. Rep.2, 342 (2012).
  210. Squartini, T., Van Lelyveld, I. & Garlaschelli, D. Early-warning signals of topological collapse in interbank networks. Sci. Rep.3, 3357 (2013).
  211. Suweis, S. & D’Odorico, P. Early warning signs in social-ecological networks. PLoS ONE9, e101851 (2014).
  212. Dakos, V. & Bascompte, J. Critical slowing down as early warning for the onset of collapse in mutualistic communities. Proc. Natl Acad. Sci. USA111, 17546–17551 (2014).
  213. Kuehn, C., Zschaler, G. & Gross, T. Early warning signs for saddle-escape transitions in complex networks. Sci. Rep.5, 13190 (2015).
  214. Bauch, C. T., Sigdel, R., Pharaon, J. & Anand, M. Early warning signals of regime shifts in coupled human–environment systems. Proc. Natl Acad. Sci. USA113, 14560–14567 (2016).
  215. Majdandzic, A. et al. Multiple tipping points and optimal repairing in interacting networks. Nat. Commun.7, 10850 (2016).
  216. Sun, E. D., Michaels, T. C. T. & Mahadevan, L. Optimal control of aging in complex networks. Proc. Natl Acad. Sci. USA117, 20404–20410 (2020).
  217. Sanhedrai, H. et al. Reviving a failed network through microscopic interventions. Nat. Phys.18, 338–349 (2022).
  218. Majdandzic, A. et al. Spontaneous recovery in dynamical networks. Nat. Phys.10, 34–38 (2014).
  219. Lin, Z.-H. et al. Non-Markovian recovery makes complex networks more resilient against large-scale failures. Nat. Commun.11, 2490 (2020).
  220. Zhou, D. & Elmokashfi, A. Network recovery based on system crash early warning in a cascading failure model. Sci. Rep.8, 7443 (2018).
  221. Pan, X. & Wang, H. Resilience of and recovery strategies for weighted networks. PLoS ONE13, e0203894 (2018).
  222. Smith, A. M. et al. Competitive percolation strategies for network recovery. Sci. Rep.9, 11843 (2019).
  223. Pasqualetti, F., Zhao, S., Favaretto, C. & Zampieri, S. Fragility limits performance in complex networks. Sci. Rep.10, 1774 (2020).
  224. Di Muro, M. A., La Rocca, C. E., Stanley, H. E., Havlin, S. & Braunstein, L. A. Recovery of interdependent networks. Sci. Rep.6, 1–11 (2016).
  225. Artime, O., d’Andrea, V., Gallotti, R., Sacco, P. L. & De Domenico, M. Effectiveness of dismantling strategies on moderated vs. unmoderated online social platforms. Sci. Rep.10, 14392 (2020).
  226. De Domenico, M., Lima, A., Mougel, P. & Musolesi, M. The anatomy of a scientific rumor. Sci. Rep.3, 1–9 (2013).
  227. Liu, R., Chen, P., Aihara, K. & Chen, L. Identifying early-warning signals of critical transitions with strong noise by dynamical network markers. Sci. Rep.5, 17501 (2015).

（参考文献可上下滑动查看）



复杂网络瓦解读书会


从复杂网络的构建到智能优化的演化，理解网络的鲁棒性与瓦解机制始终是一个深刻的挑战。更值得深思的是，网络的结构和算法设计如何决定了网络在遭遇局部攻击时的脆弱性，及其整体瓦解的速度与范围。动态演化过程中的节点和边的变化，也会影响系统如何在瓦解中保持部分功能，或如何适应新的结构。因此，网络瓦解研究聚焦于一个核心问题：在不同类型的网络结构（如高阶网络、空间网络、时序网络）中，局部的破坏如何引发整体功能的丧失？在面对网络的异质性和约束条件下，不同的优化算法如何有效识别并摧毁关键节点与连接，从而最大化网络的瓦解效应，进而影响系统的整体稳定性与韧性？

集智俱乐部联合北京师范大学教授吴俊、国防科技大学副研究员谭索怡、北京化工大学副教授谷伟伟、中国科学技术大学博士后范天龙、国防科技大学在读博士卿枫共同发起「复杂网络瓦解读书会」，跨越网络结构、算法模型与应用场景的视角，探索复杂网络瓦解的前沿进展。重点探讨不同算法与优化框架如何帮助我们认识网络的脆弱性，并在现实约束下推动网络系统的智能演化与应用发展。

图片

详情请见：复杂网络瓦解读书会启动：从结构脆弱性到智能优化前沿


推荐阅读

1. Nature Physics评论：复杂系统的内在简单性
2. Physics Reports重磅综述：网络韧性及核心研究主题
3. 如何以最小代价破坏系统结构？一套基于机器学习的方法
4. 涌现动力学如何用来分析复杂系统？ | 新课上线
5. 集智学园精品课程免费开放，解锁系统科学与 AI 新世界

6. 高考分数只是张入场券，你的科研冒险在这里启航！

7. 重整化群与非线性物理，寻找复杂系统跨尺度的分析方法丨新课发布



点击“阅读原文”，报名读书会