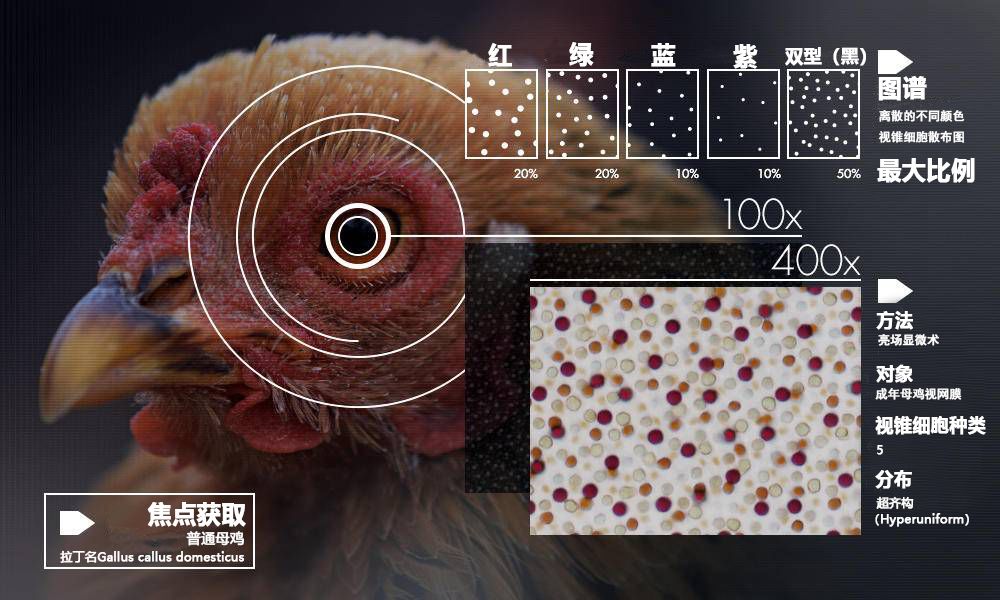
鸡的视锥细胞图谱

导语

和人类相比，鸟类有更多种类的视锥细胞，而这些细胞的排列方式中隐藏着进化奥秘。一起阅读本文，了解这个横跨数学、物理、化学、生物的神秘问题。

编译：集智翻译组

来源：quantamagazine.org

原题：A Bird’s-Eye View of Nature’s Hidden Order

在鸟类的眼睛、盒装的玻璃弹珠和其他匪夷所思的地方出现的神秘排列模式引起了科学家们的关注。

七年前，Joe Corbo从鸡的眼睛中看到了惊人的东西。覆盖视网膜的、对颜色敏感的视锥细胞（从鸡的眼睛中分离而来），在显微镜下呈现为五种不同颜色与大小的波卡圆点。然而Corbo观察到，不同于人类视锥细胞的随机分散以及鱼类视锥细胞的整齐排列，鸡视锥细胞的分布看似杂乱无章却又相当均匀。尽管这些细胞的排布没有明显的规律，但它们之间的距离不会太近或太远。五种视锥细胞散布在视网膜上，如明暗不同的星星点缀在夜空里，无论是其中任何一种视锥细胞，还是所有视锥细胞的集合，都呈现出同样引人注目的随机性与规律性的结合。圣路易斯华盛顿大学（Washington University in St. Louis）生物实验室的Corbo完全被这一现象迷住了。

“仅仅看着这些图案，就能感受到它们的美丽！我们被这美丽吸引，纯粹出于好奇而渴望更好地理解这些图案。”Corbo和他的合作者希望能够找寻出图案的功能以及形成过程。但是当时他并不知道，原来同样的问题在众多其他的语境中屡被提及。他的发现，使得在数学和物理中屡屡出现的隐藏秩序，第一次找到了生物表现形式。

Corbo所确信的是，这个问题的答案应该从鸟类视网膜本身的功能入手。鸟类具有惊人的视觉功能，例如，老鹰可以从一英里外的高空搜寻到老鼠的踪迹。他的实验室正致力于研究鸟类获得出色视觉能力的进化适应性机制。

1.鸟类眼睛中的

超齐构体

3亿年前，一种类似蜥蜴的生物逐渐进化为恐龙和原始哺乳动物。而恐龙正是鸟类的祖先，因而，鸟类视觉许多令人惊异的属性，被认为是从这些类似蜥蜴的生物那里继承而来。在恐龙统治地球上栖息地的漫长时间里，我们的哺乳动物近亲只能在黑暗中仓皇奔走，成为战战兢兢的夜行生物，逐渐丧失了辨别色彩的能力。在那时，哺乳动物的视锥细胞减少到了两个——这是一个进化史上的低谷，至今人类仍然试图从这一低谷中摆脱出来。幸运的是，大约3000万年前，我们的一支灵长类祖先的视锥细胞分裂出红、绿两种颜色的感知功能，与原本就存在的感知蓝色的视锥细胞一起，形成了人类的三色视觉。然而人类的视锥细胞，尤其是较年轻的感知红色与绿色的视锥细胞，分布呈块状且杂乱无章，对于光的探测也不均匀。

与哺乳动物不同，鸟类的眼睛经过了亿万年时间的优化。随着视锥细胞数目的增加，其空间排布更为规律。然而，Corbo和同事们好奇，为什么视锥细胞的分布没有进化为网格或“晶格”那样完全规律性的排列方式？一种看起来最有可能的解释是，他们在视网膜观察到的奇怪的、难以分类的图案，是在某种未知约束条件下的最优状态。这些约束条件是什么？图案意味着什么？鸟类视觉系统是如何演化成现在的样子的？这些问题仍然不清楚。生物学家已经尽力量化视网膜的规律性，然而这是一个他们不熟悉的领域，他们需要帮助。

2012年，Corbo联系了普林斯顿大学的理论化学教授Salvatore Torquato，他是研究“堆积”问题（Packing problem）的专家。所谓的“堆积”问题，是指在给定的空间维度下，如何排布物体以最大限度地塞满有限空间，在鸟类视觉问题中，就是如何将五种不同尺寸的视锥细胞最致密地排布在二维的视网膜上。

“我想知道鸟类视觉系统是否是属于最优的排布方式。”Corbo说道。Torquato对这个问题同样感到好奇，他在视网膜图案的数字图像上运行了一些算法，结果让他“感到震惊”，Corbo回忆说，“他发现，原本在无机物或物理系统中看见的现象，竟然同样出现在鸟类视觉系统中。”

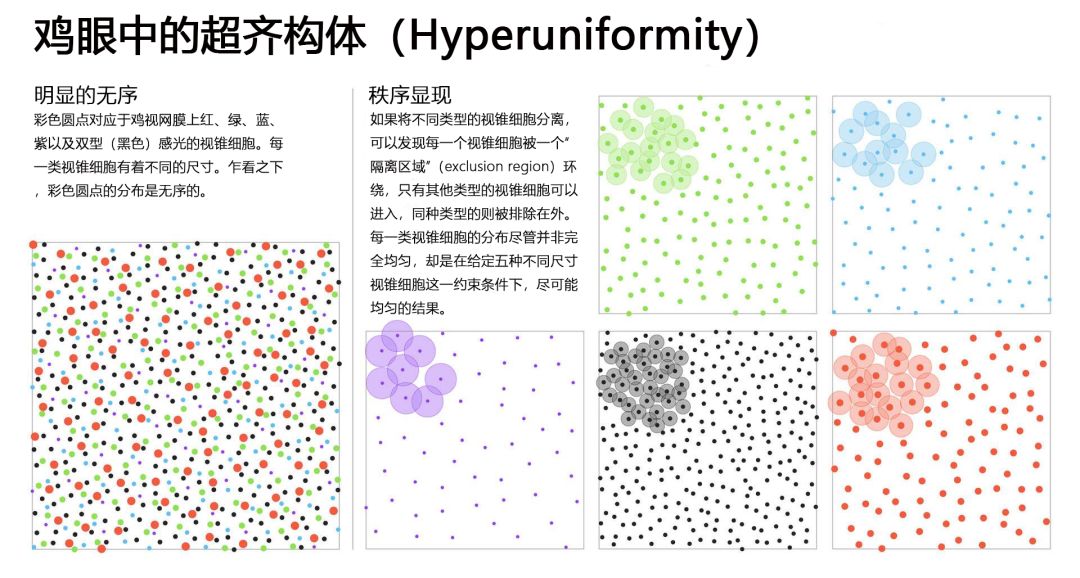
鸡眼中的超齐构体

（Hyperuniformity）

从21世纪初，Torquato已经开始对这一全新的分布模式进行研究，他将其称为“超齐构体”（hyperuniformity）。（相比于同一时期由罗格斯大学（Rutgers University）的Joel Lebowitz提出的“超同质体”（superhomogeneity），这一名称更为合适。）从那时起，超齐构体现象开始广泛出现在不同的系统中。除了鸟类的眼睛，超齐构体也出现在准晶材料、随机数矩阵、宇宙的大尺度结构、量子系综以及乳浊液与胶体等软物质系统中。

当某些现象出现在一些新的领域中时，科学家们往往会为之惊喜，这种感觉就好像和宇宙玩”打地鼠“游戏一样。探索这种现象背后隐藏的普遍真理是科学家门最为热衷的工作。在这个过程中，他们发现了很多超齐构材料具有实用价值的新特性。

从数学的角度来看，超齐构体的研究也很有价值。“我对它的研究越深入，就越能感受到它原理上的优雅以及这一概念令人惊叹的地方。”新英格兰微软研究所的数学家、研究堆积问题的专家Henry Cohn说。“另一方面，让我惊讶的是超齐构体广泛的应用前景。”

13年前，Torquato和一位同事发起了超齐构体的研究，他们从理论上描述了这个问题，并给出了一个简单而又令人惊讶的例子：“将（各种大小的）玻璃弹珠放进一个容器里，摇动它们直到塞满容器为止，这时候系统是超齐构的。”今年春天，Torquato在他普林斯顿大学的办公室说道。

上述玻璃弹珠的排布模式在学术上被称为“最大随机满塞堆积”（maximally random jammed packing），这种排布方式可以填充64%的空间（其余部分是空气）。这比球体可能的最密堆积要小——在箱子里填满桔子的晶格堆积（lattice packing），可以填充74%的空间。但是晶格堆积并非总能实现，我们并不能轻易地将一箱玻璃弹珠摇动成晶格堆积。同样地，五种不同尺寸的物体也很难排列形成晶格结构，例如鸡眼中的视锥细胞，Torquato解释说。

堆积问题

我们考虑用水平桌面上的硬币来代替视锥细胞。“如果压缩一堆一美分硬币，硬币会形成三角晶格堆积；然而，如果向其中加入一些与之尺寸不同的五美分硬币，则会阻止硬币形成晶格堆积。如果有五种不同尺寸的硬币，比如继续加入25美分硬币，50美分硬币，或者其他不同尺寸的硬币——会进一步抑制晶格堆积的形成。”Torquato说。

类似地，几何学原理要求鸡的视锥细胞呈无序排列。然而，进化过程中的激烈竞争又要求视网膜尽可能均匀地接收光线：接收蓝光的视锥细胞彼此远离，接收红光的视锥细胞则彼此远离，等等。这些要求的平衡会使系统最终“呈现出无序超齐构体的特征”。

超齐构体使鸟类的视角具备了两种优势：既有多达五种的感知颜色的视锥细胞，又让每种细胞近乎均匀地排布在视网膜上，为鸟类提供了显著的颜色分辨能力。然而，这种“隐藏的秩序，人类无法通过自己的眼睛感受到。“他说。

马赛克图案：看似无序排列（小尺度的无序）的彩色小石子拼接出生动的图案（大尺度的规律） | 来源：Wikipedia

确定一个系统是否是超齐构体所需要的算法类似于套圈圈那样的游戏。

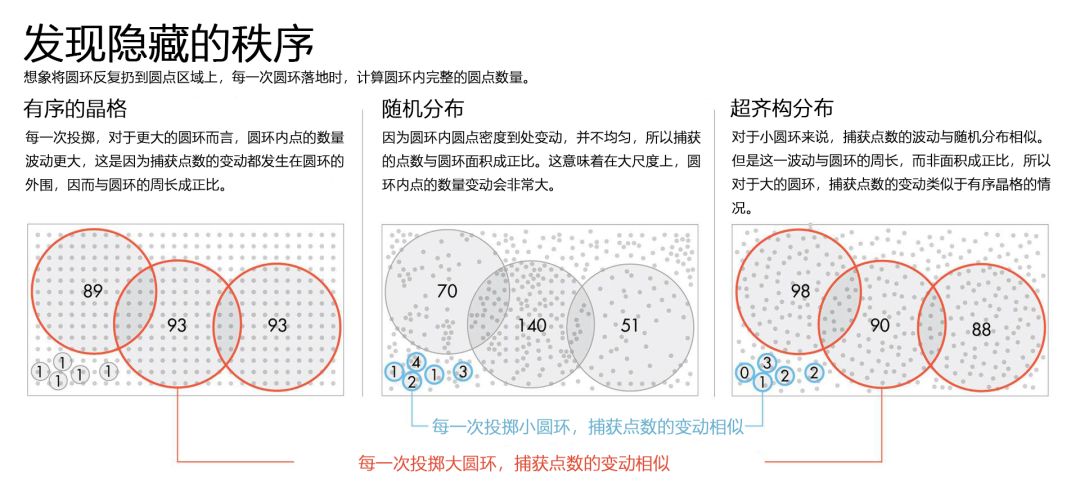
（1）首先，Torquato解释道，想象将圆环反复扔到有序的晶格上，每一次圆环落地时，计算圆环内的点数。圆环捕获的圆点数量从一次投掷到下一次投掷有所波动，但是波动并不大。这是因为圆环内部总是覆盖固定数量的圆点，捕获点数的唯一变化发生在圆环外围。如果增加圆环的尺寸，波动将会发生在更长的圆周上。因此，对于晶格分布，捕获的点数（或晶格中的“密度波动”）的波动与圆环周长成正比。（在更高维度，密度波动也与维数减去一成正比。）

（2）现在再来想象在一些随机分布的点上玩套圈圈游戏。随机分布的点往往形成空隙与团簇，并不均匀。随机分布的一个特点是，当圆环变大时，被捕获的点数与圆环面积成正比，而不是周长。结果就是，在大尺度上，在不同次投掷之间，密度波动比晶格分布要极端得多。

（3）当涉及到超齐构分布时，游戏变得更加有趣。因为点的分布是局部无序的，所以对于小圆环，相邻两次投掷捕获点数的波动比晶格分布的要大，与随机分布相似。然而随着圆环变大，密度波动的增长逐渐与圆环的周长成正比，而不是圆环的面积。这意味着，大尺度下，超齐构分布与晶格分布一样均匀。

普林斯顿大学的物理学家Paul Steinhardt说，在超齐构系统中，研究人员发现了更多“结构生态规律”：在超齐构系统中，密度的波动与圆环周长的n次幂成正比，幂指数n通常在1和2之间，并且乘以不同的系数。

“这一切意味着什么呢？我们不知道。研究仍在进行中，很多论文有待发表。”Torquato说。

2. 材料大观园

超齐构体显然是很多不同系统共有的一种状态，然而，对于其普遍性的解释仍是一项正在进行的工作。“我认为，超齐构体本质上是某种更深层优化过程的标志”，Cohn说，至于这些过程是什么，“对于不同问题可能差别很大。”

超齐构系统分为两大类。第一类，是系统达到平衡时自发形成的超齐构体。例如准晶——一种奇异的固体，其内部彼此连结的原子不遵循重复规律排布，但能形成密铺空间（tessellate space）——系统达到平衡时，表现为超齐构体。

在这些平衡系统中，是粒子间的斥力将彼此分开，并形成全局的超齐构体。与之相似的数学原理或许能够解释鸟类眼中超齐构体的出现，随机数矩阵的本征值分布，以及黎曼Zeta函数（就是那个可以推出素数有无限多个的函数）的零点分布等数学问题。

另一类超齐构系统是“非平衡”系统，晃动后的玻璃弹珠、乳浊液、胶体以及冷原子系综都属于这类系统。组成系统的粒子相互碰撞，但不存在相互斥力。系统必须在外力作用下，才能形成超齐构状态。而在这类非平衡系统中，还存在着更为棘手的分类。

去年秋天，以法国里昂高等师范学校Denis Bartolo为代表的物理学家们，在Physical Review Letters上发表文章称，以精确的特定振幅晃动乳液，可以形成超齐构体，这一特征振幅标志着材料可逆性与不可逆性的临界转变：如果晃动比临界振幅轻，乳液中悬浮的粒子在晃动之后会回到之前的相对位置。如果晃动比临界振幅剧烈，粒子的运动则不可逆转。

Bartolo的工作表明，在非平衡系统中，可逆性的开始与超齐构体的出现之间存在着根本(尽管不是完全)的联系。然而，最大随机满塞堆积的原理则是完全不同的理论。

“我们能连接这两种系统的物理现象吗？”Bartolo问道，“根本不行。对于超齐构体为什么会在两种截然不同的物理系统中出现，我们一无所知。”

当科学家们努力串联这些线索时，他们发现了超齐构材料令人惊讶的特性——超齐构材料具备一些晶体的特性，而且不容易受到制造误差的影响，它们更类似于玻璃，或其他没有相关性的物质。

在Optica上新发表的一篇论文中，以Rémi Carminati为代表的法国物理学家报告说，致密的超齐构材料可以制作成透明材料，然而，同样密度的非关联无序材料却是不透明的，隐藏在粒子相对位置中的规律导致散射光干涉并且抵消。“干涉会破坏散射。光穿过材料，仿佛材料是均匀的。”Carminati解释道。现在要知道这种致密、透明、非晶体的材料会有什么应用，还为时尚早。但是“肯定有潜在的应用”，尤其在光子学领域。

Bartolo最近关于超齐构体如何在乳液中形成的发现，可以转化成简易配方，用于搅拌混凝土、化妆品膏体、玻璃和食物等。“每当要分散糊状物内的粒子时，就需要处理固体颗粒的混合问题。这可以作为均匀分散固体颗粒的一种方法。”

首先，确定材料的特征振幅，然后多次以这一振幅晃动材料，这样，均匀混合的超齐构分布就出现了。“我不应该免费告诉你这些，而应该创建一个公司！”Bartolo说。

Salvatore Torquato，普林斯顿大学的理论化学家，从21世纪初就开始研究超齐构体。

事实上，Torquato、Steinhardt和同事们已经这样做了。他们创建的公司Etaphase，将生产超齐构光子电路——一种通过光而非电子传输数据的设备。几年前，普林斯顿大学的科学家发现，超齐构材料存在“带隙”（band gap），可以阻止特定频率的传播。带隙使得数据的受控传输成为可能，因为被阻挡的频率可以被波导（waveguide）容纳和引导。

带隙曾被认为是晶格特有的，其传输方向必须与晶体的对称轴方向一致。这意味着，光子波导只能在特定的方向上传播，限制了它作为电路的用途。

因为超齐构材料没有传输方向方向的限制，我们知之甚少的带隙可能会更有实际用途，使“弯曲的波导，并且是任何希望的波导”成为可能，Steinhardt说。

鸟类眼中五种颜色的马赛克图案被称为“多视锥超齐构体” （multihyperuniform），至今为止，在自然界是独一无二的。

Corbo仍然没有精确地说明这些图案是如何形成的。它是因为视锥细胞的彼此排斥而出现？还是因为视锥细胞像玻璃弹珠一样被晃动成如此形态？他更倾向于前者。

细胞可以分泌分子，排斥同一类型的细胞，但对其他类型的细胞没有影响。或许在胚胎发育过程中，每个视锥细胞都会发出信号，表明它将分化成某种类型，以防止临近的细胞做同样的事情。“这不过是一个解释事情可能是如何发展的简单模型。每一个细胞的局部行为创造了全局模式。”

除了鸡这种最容易获得的、用于实验室研究的家禽，同样的“多视锥超齐构体”图案也出现在Corbo研究过的其他三种鸟类的视网膜中，表明这种进化适应性是普遍的，而非某种特定环境下的产物。