分形结构最大程度地利用了细胞表面积来运输能量

导语

Geoffrey West 等人1999年在Science 发表了一篇文章，用分形几何来解释生物异速标度律，引申出了生命的“第四维度”。集智俱乐部“幂律与规模”读书会上，对生命3/4标度现象如何起源、4是否意味着生命有第四维度、如何从分形的角度理解维度等问题，做了大量探讨，本文是对“生命第四维”问题探讨后的一篇笔记。

该论文题目：

The Fourth Dimension of Life: Fractal Geometry and Allometric Scaling of Organisms

下载地址：

http://biology.unm.edu/jhbrown/Documents/Publications/WestBrown&Enquist1999S.pdf

自然选择使生命的代谢能力最大化，最大限度地扩大了运输资源和能量的表面积。例如我们的代谢能量会通过毛细血管的表面积运向全身上下细胞，从而促进细胞生长，维持生命所需的能量。

举个很直观的例子，尽管你的肺只有一个足球那么大，体积为5～6升，但是，血液中负责氧气和二氧化碳交换的肺泡总表面积，几乎有一个网球场那么大；而所有气流通路的总长度几乎是从伦敦到莫斯科的距离，约2500千米！

这是怎么做到的呢？

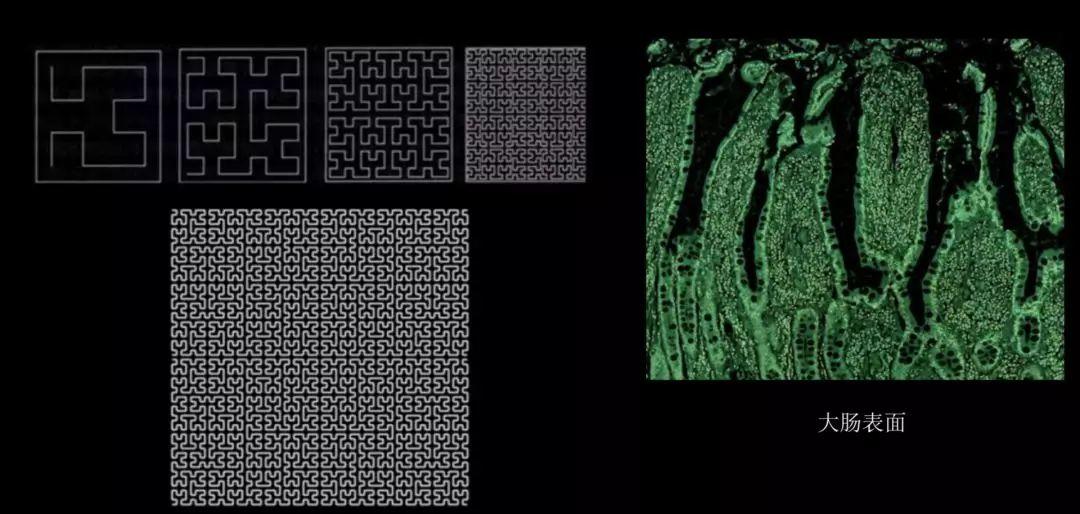
Peano曲线和大肠表面的分形褶皱

答案是分形。分形是20世纪系统科学提出的一个重要概念，它可以对d维的几何体施加最大化的褶皱和扭曲而得到d+ 1维的几何体。例如褶皱的大脑皮层，以及扭曲缠绕的大肠。生命体内正是充满了神奇的分形结构，才实现了空间填充的最大化。

以上选自：

如何将生命体装入旅行箱？| 《规模》

克莱伯定律揭秘生命第四维

即便在“不经意间”已经处处运用分形结构解决难题，但或许我们对其并没有系统的认识。理解分形，从认识维度开始。

什么是维度

维度，又称维数，在数学中被定义为独立参数的数目，在物理学和哲学的领域内，是指独立的时空坐标的数目。

0维是一个点，没有长度；

1维是一条线，只有长度；

2维是一个面，由长度和宽度形成的面；

3维是一个体，在2维的基础上加上高度所形成。

1维的线在其维度方向可以截出无穷多个0维的点；

2维的面从任意维度方向可以截出无穷多的1维的线；

3维的体可以截出无穷多的2维的面；

4维则是建立在3维之上又多一个维度，根据上面的概念的引申，4维的东西可以截出无穷多个“体”。

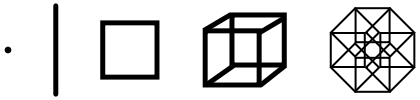
图1 从0-4的维度示意图 |wikipedia

在物理学上往往将时间作为第四维，与空间的3维一起构成4维时空，在任何时间来看（横截观察），就可以得到一个“体”。如果固定空间的一个维度，剩下的两个维度和时间也可以合成一个体，可以形象地展示物体的运动情况，如图2所示。

图2太阳系在银河系中的真实运动轨迹 |wikipedia

维度是这个形体上确定一个位置所需要的独立坐标的个数。对于一个独立的点来说，它没有大小，确定点上的位置不需要任何坐标数据。但对于一条直线来说，就需要用坐标来确定线上点的位置。曲线也是如此。无论直线还是平面上的曲线还是空间上的连续曲线都只有一个维度。

平面和球面都是2维的，因为一个数据无法标定面上的某个具体位置，而是需要并且只需要2个数据。比如地球上的任何一个位置通过精度和维度就可以确定下来。

弯曲的三维形态难以想象，因为其要存在至少4维的空间中。

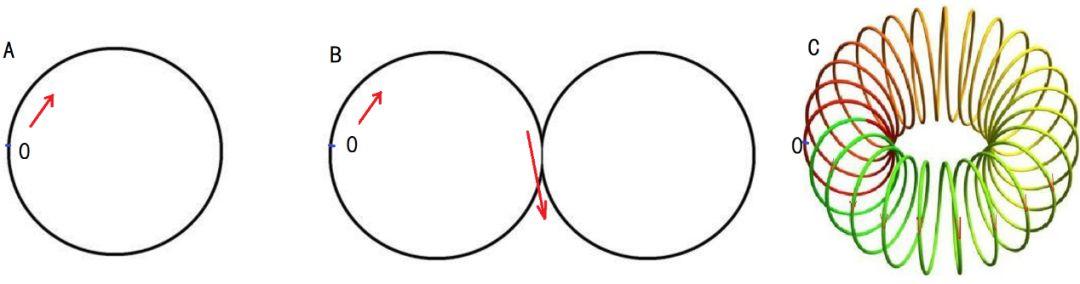
图3 平面和空间中的曲线，也都是1维的

曲线是一维的，如图3所示，这些曲线，无论是平面上的还是立体中的都是1维的，都可以通过一个数值来确定某个位置。

虽然一般人已经习惯了整数维，但有些时候维度不一定是整数，例如分形，维度可能会是一个非整的有理数或者无理数。

如何理解分形的维度

下面将介绍分形中最著名的几个例子。

A.康托(Cantor)三分集

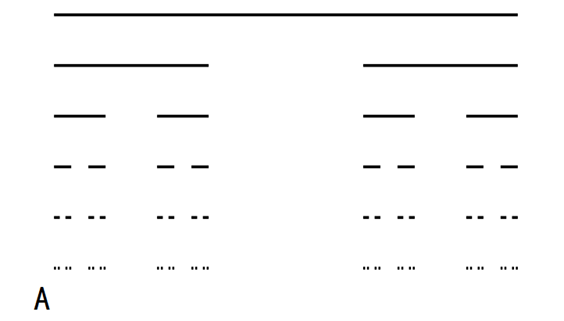
1883年，德国数学家康托(G.Cantor)提出了如今广为人知的康托三分集。康托三分集的构造过程是：

把闭区间[0，1]平均分为三段，去掉中间的 1/3 部分段，则只剩下两个闭区间[0，1/3]和[2/3，1]。
再将剩下的两个闭区间各自平均分为三段，同样去掉中间的区间段，这时剩下四段闭区间：[0，1/9]，[2/9，1/3]，[2/3，7/9]和[8/9，1]。
重复删除每个小区间中间的 1/3 段。如此不断的分割下去，最后剩下的各个小区间段就构成了康托三分集。

康托三分集的维度为D=log2 / log3=0.631

B.科赫雪花。

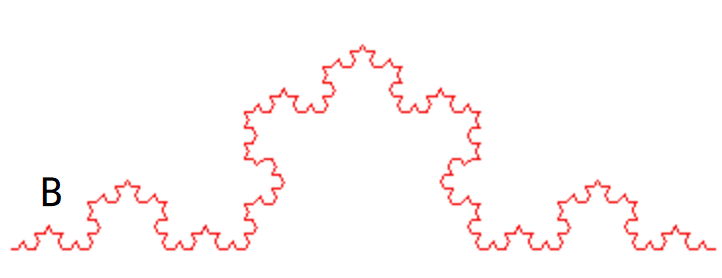
瑞典人Koch于1904年提出。给定线段AB，科赫曲线可以由以下步骤生成：

将线段分成三等份，形成3个线段
以中间段为底，向外（内外随意）画一个等边三角形
将这个中间段移去
分别对目前的4个线段，重复1~3

科赫雪花维度为D=log4 / log3=1.2618

C.门格海绵

1926年被奥地利数学家 Menger 首次描述。门格海绵的结构可以用以下方法形象化：

从一个正方体开始，把正方体的每一个面分成9个正方形。
再将把正方体分成27个小正方体，像魔方一样。
把每一面的中间的正方体去掉，把最中心的正方体也去掉，留下20个正方体（第二个图像）。
把每一个留下的小正方体都重复前面的步骤。

把以上的步骤重复无穷多次以后，得到的图形就是门格海绵。

门格海绵的维度为D=log20 / log3=2.7268

再次强调，维度是这个形体上确定一个位置所需要的独立坐标的个数。

确定康托集上的某一个位置不需要整个实数域，因为有很多点已经挖去了。所以可以认为康托集要比一个点多，但不如一个曲线多。维度应该在0-1之间。维度应该在0-1之间。

而科赫雪花是在二维平面内，但是没有覆盖整个平面，确定上面的位置一个实数是不够的，例如给定横轴方向的实数而不指定纵轴位置的话无法确定集合上的一个元素，但纵轴并不是连续的，只有某些位置上才会有意义，所以应该大体上维度介于1-2之间。

而门格海绵用不着3个独立的变量来确定一个位置，所以维度应该在2-3之间。从这个意义上讲，能表示在二维平面的分形的维数不能超过2，在立体空间表示出来的分形不会超过3。

所以，West在生命第四维的文章中说V（和体积和质量有关的东西）是4维的，很容易受到的质疑。

严格的分形维度如何定义

严格的分形维度的定义为 Hausdorff 维数，可以通过覆盖来进行解释。

Hausdorff 提出：假设考虑的物体或图形是欧氏空间的有界集合 ,用半径为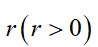

的球覆盖其集合时 , 假定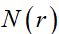是球的个数的最小值,则有分形维数。

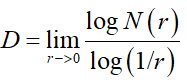我们先说一个长度为L的直线段，如果我们用更小的球去覆盖，则需要的个数会随着球的半径减少而增加，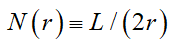

所以分形维数：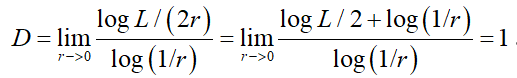

同理很容易说明平面是2维以及立体是3维的。

再来看康托集。假设整个长度为1，用最长的长度为1的直线段即可覆盖，但如果用长度为1/3的线段的话，就不用3个了，两个即可，因为中间是空的。继续进行，若长度为1/9的线段的话，只需要4个线段。

所以当线段的长度变为上一个覆盖的1/3的时候，需要的个数只增加到两倍。

所以分形维数：。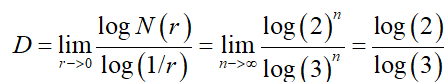

同样，对于科赫雪花，当使用长度为原来1/3的线段进行覆盖时候，覆盖物的个数会增加到4倍，

所以分形维数：。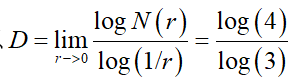

生命第四维是一种类比

回到 West 关于生命第四维的文章，其目的是解释生物基础代谢率与生物量（质量）之间的非线性关系，更精确地说是3/4的幂律关系。也就是如果生物体体重增加一万倍（10的四次幂），代谢率只增加到原来的一千倍（10的3次幂）。

West 在这个文章中运用Koch雪花那样的“分形可以增加维度”的思想，将血管横截面圆周分形化，从1维变为2维，将整个血管的表面积变为3维，并将其与基础代谢率建立线性关系。而体积和质量相关部分为表面积的维度再增加一个维度变为4维。维度关系如下表所示。

表1 生物体血管的分形维度和传统的欧氏几何维度的关系

和体积有关的东西超过3维，是很难被接受的。集智学友在 West 访华期间向其本人咨询了这个问题， West 本人答复说，这个增加的维度并非实指。

生命的第四维度，在数学上看好像是的，但严格地说——“这是一个类比和拓展”。

参考文献

https://zh.wikipedia.org/wiki/維度
http://v.youku.com/v_show/id_XNTYzNzQ4OTY0.html
https://baike.baidu.com/item/分形理论/1568038?fr=aladdin
https://www.cnblogs.com/WhyEngine/p/3998063.html
https://www.cnblogs.com/WhyEngine/p/3981674.html
https://baike.baidu.com/item/%E9%97%A8%E6%A0%BC%E6%B5%B7%E7%BB%B5/9005082?fr=aladdin
West G B, Brown J H, Enquist B J. The fourth dimension of life: fractal geometry and allometric scaling of organisms[J]. science, 1999, 284(5420): 1677-1679.
朱金兆, 朱清科. 分形维数计算方法研究进展[J]. 北京林业大学学报, 2002, 24(2): 71-78.
http://www.math.ubc.ca/~cass/courses/m308-03b/projects-03b/skinner/ex-dimension-koch_snowflake.htm