摘要

复杂系统的多尺度建模对于理解其内在机理至关重要。近年来，数据驱动的多尺度建模已成为应对复杂系统挑战的有效途径。然而目前该领域更聚焦于特定领域的预测或控制问题，尚缺乏合适的理论框架来推动复杂系统建模理论的建立。另一方面，自相似性普遍存在于复杂系统中，这暗示着大规模复杂系统的建模成本可能得以降低。本文提出一种将自相似性作为先验知识的多尺度神经网络框架，可有效建模自相似动力系统。该框架不仅能判别确定性动力学是否具有自相似性，对于不确定性动力学，不仅能判定其是否自相似，还能通过比较确定哪组参数更接近自相似。通过从动力学中提取尺度不变核，我们的框架可实现任意尺度的建模。此外，该方法能准确识别自相似系统中的幂律指数，为复杂系统建模理论的建立提供了重要依据。

研究领域：自相似性（self-similarity），机器学习，动力学，复杂系统建模，多尺度神经网络

论文题目：Data driven modeling for self-similar dynamics

发表时间：2024年12月28日

论文地址：https://doi.org/10.1016/j.physd.2024.134505

期刊名称：Physica D: Nonlinear Phenomena

复杂系统的自相似性：从理论到数据驱动建模

复杂系统因其非线性、多尺度特性与涌现行为，始终是科学建模的难点。传统方法如降阶模型（ROM）和方程无关方法（EFM）虽能简化问题，但常忽略物理意义或难以推广。与此同时，自相似性（self-similarity）作为复杂系统的普遍特征，暗示了一种可能性：通过尺度不变的动力学核，以低成本建模大规模系统。然而，如何将自相似性融入数据驱动的建模框架，仍是一个开放问题。

近期，集智研究中心参与发表在 Physica D 的一篇研究提出了一种融合自相似性先验的多尺度神经网络框架，旨在通过机器学习揭示复杂系统的尺度不变规律。这一工作不仅为自相似动力学的识别提供了新工具，还首次实现了动力学重整化策略的自动化学习，为理解临界现象和相变开辟了新路径。

自相似动力学的定义：从微观到宏观的一致性

自相似动力学的核心在于跨尺度的一致性。研究团队将其形式化定义为：若微观状态X经粗粒度映射$$P$$得到宏观状态Y，且两者的动力学方程和参数在形式与数值上保持一致，则称系统具有自相似性。这一过程通过一致性指标（consistency）量化：若微观演化一步后的粗粒度结果Y_t+1 与直接粗粒度微观状态  的均方误差趋近于零，则系统满足自相似性。该定义兼容确定性与随机性系统，还可以比较不同参数组下的自相似程度。

框架设计：

动力学学习器与粗粒度学习器的协同

根据上述形式化定义，研究使用多尺度神经网络方法，设计了双模块神经网络架构，包括动力学学习器和粗粒度学习器两个主要组成部分（图 1）。

1. 动力学学习器（Dynamics Learner）：通过卷积神经网络（CNN）捕捉微观态的演化规则，将神经网络参数有效地作为动力学参数，优化的目标是最小化实际值和预测值之间的差异。考虑到微观和宏观尺度之间数据维度的差异，即宏观变量通常较少，因此设计具有时空平移不变性的神经网络非常重要。只有这样，才有可能将在微观动力学数据上训练的动力学学习器应用到宏观动力学中。

2. 粗粒度学习器（Coarse-graining Learner）：学习从微观态到宏观态到映射，保证宏观动力学的形式和参数应该与微观动力学相同，并且可以据此实现宏观动力学的准确预测。此外，通过解码器防止映射坍缩为平凡解。

两模块分阶段训练：首先优化动力学预测误差，再固定动力学参数，联合优化粗粒度与解码器的重建误差。这种设计确保宏观动力学与微观规则同构，同时避免传统方法中参数耦合导致的训练不稳定。

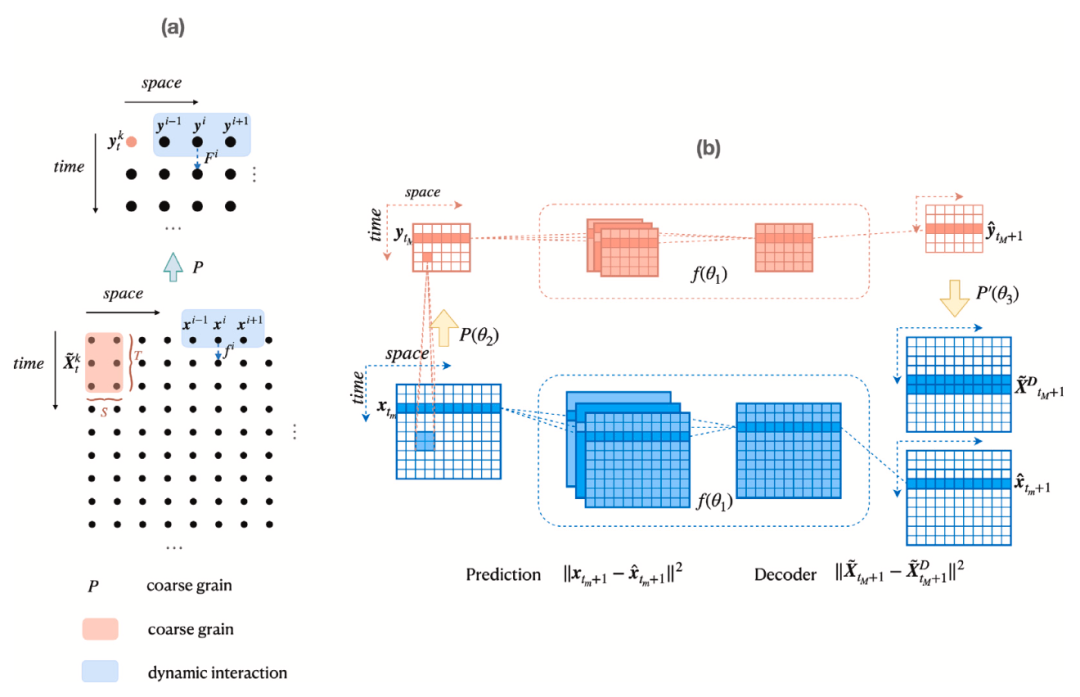
图 1.（a）二维晶格系统中动力学和粗粒化的示意图。蓝色区域表示动力学相互作用的范围，此处以最近邻相互作用为例。蓝色虚线箭头表示xⁱ或yⁱ在动力学fⁱ或Fⁱ下演进一步。红色区域表示微观状态的基本单位，将是粗粒度的宏观状态，在上图中显示为红点。动力学和粗粒化算子可以应用于任何其他状态和区域，这意味着算子是均匀的。（b）该框架中使用了卷积神经网络CNN模型，共有两个层级的神经网络框架。第一层级旨在利用图中底部呈现为蓝色的微观状态来捕捉微观动力学f，而第二层级则代表宏观状态和动力学F，在图中顶部显示为红色。两个动力学都接收来自各自层级的时间序列数据作为输入，并对未来结果进行预测。微观和宏观动力学共享相同的神经网络结构和参数。鉴于微观和宏观层级之间数据维度的差异——通常宏观变量较少——这就需要构建具有时空平移不变性的神经网络。粗粒度学习器P(θ₂)将两者连接起来，促进微观数据到宏观数据的转换。为防止在训练过程中宏观状态陷入平凡状态，我们在宏观预测之后添加了一个解码器P'(θ₃)。该解码器约束其输出与微观状态极为相似。训练完成后，解码器可停用。

实验验证：从元胞自动机到活性物质系统

研究通过三类系统验证框架的有效性：

1. 确定性的元胞自动机（CA）：在256种规则中，框架成功识别出21种自相似规则（如Rule 60），并自动学习其粗粒度策略。例如，Rule 60在空间尺度 S = 2或4 时，宏观规则与微观一致；而Rule 85仅在 S = 3 时满足自相似性（图2）。

2. 随机扩散过程：对连续时空的扩散方程，框架在Δt₀→0时学习到高斯型动力学核，且宏观扩散系数与微观一致（图3b）。

3. Vicsek模型：在临界噪声区域 η≈2，模型的重建误差最低（图4），表明自相似性在相变点附近最强。这与动力学重整化群理论预测的临界指数z≈2一致，验证了框架对复杂临界行为的捕捉能力。

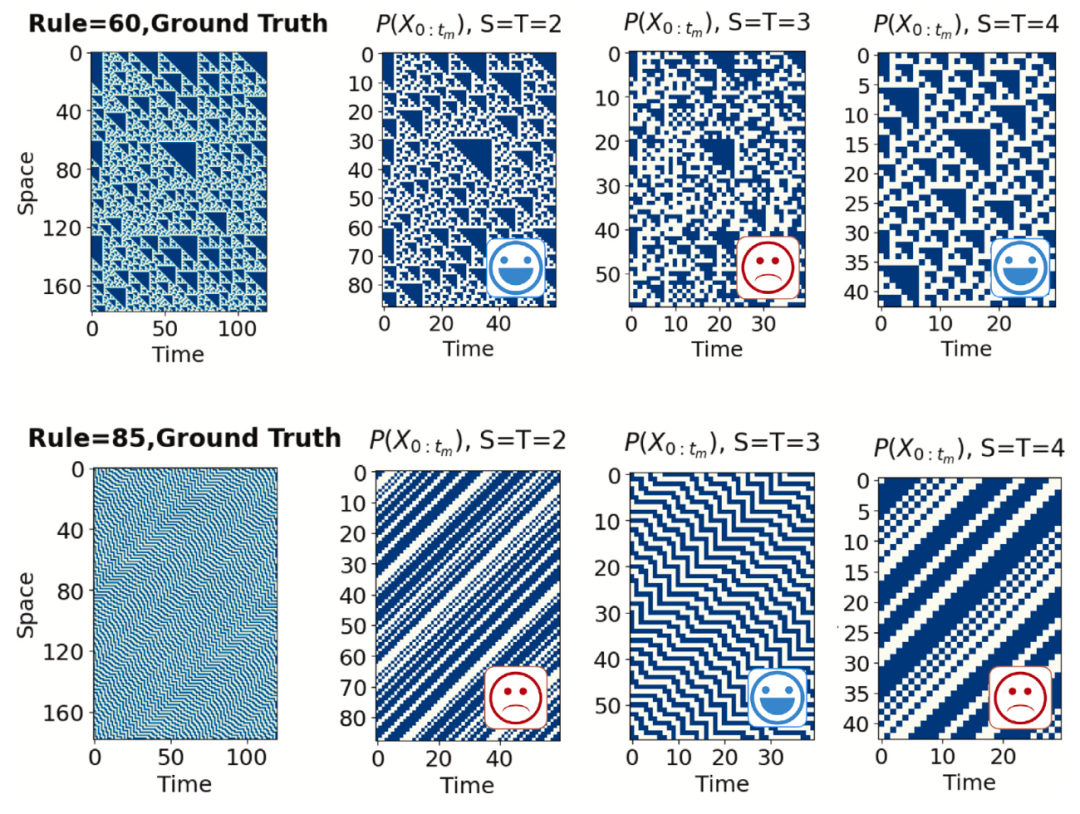
图 2. 元胞自动机根据其自相似性质的动力学粗粒化（规则60和规则85）。第一行是规则 60 的结果。它们是真实值以及三个不同尺度（分别对应 S = T = 2、3、4）的粗粒度结果。第二行是规则 85 的结果，同样也是真实值以及三个不同尺度（分别对应 S = T = 2、3、4）的粗粒度结果。我们可以看到，除了 S = T = 3 的情况，规则 60 在另外两种情况都可以在宏观层面重正化为相同的规则，而规则 85 只有在 S = T = 3 时才能重正化为自相似的动力学。

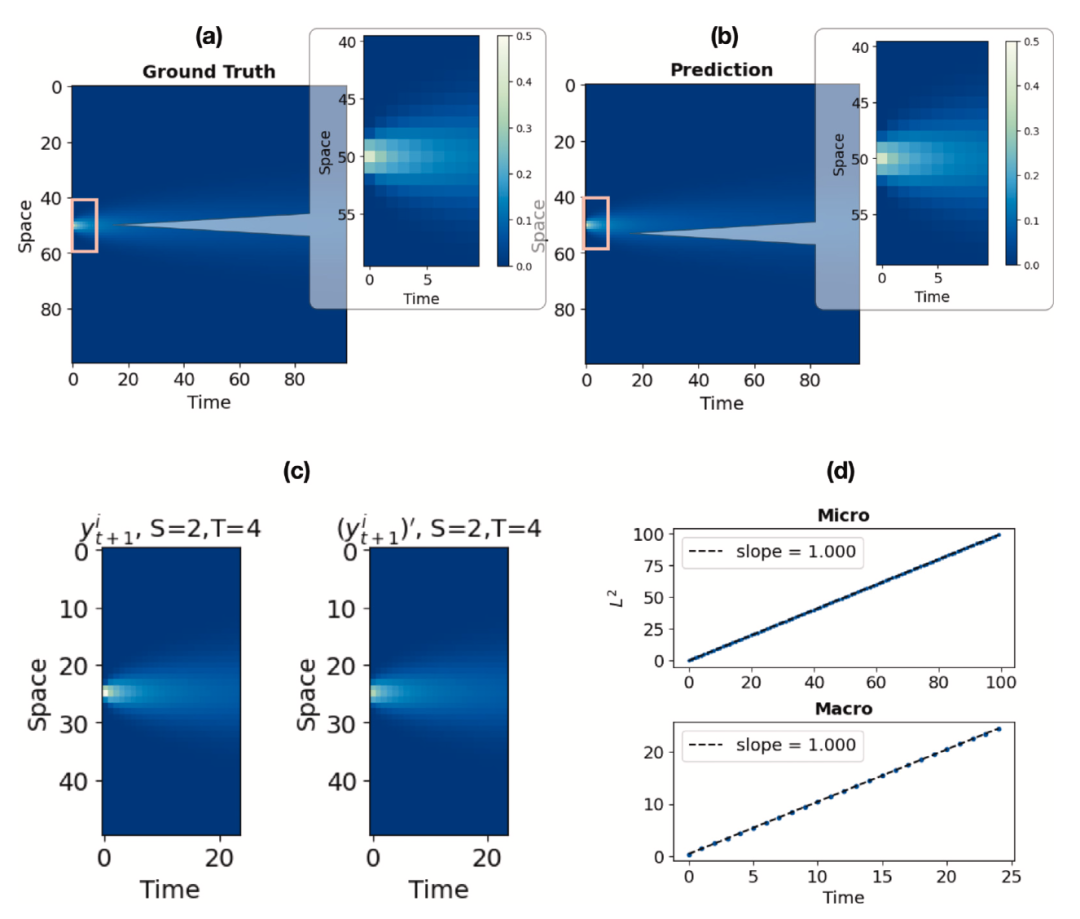
图 3. 扩散过程动力学预测与一致性结果的可视化。(a)和(b)分别表示Δt₀→0时微观状态的真实值和预测值。子图是红色方块的放大版本，以便获得更清晰的可视化。(c)为Δt₀→0时的动力学一致性可视化，与之前的CA相同。我们设置𝑆= 2和𝑇= 4为例，而𝑆= 3和𝑇= 9也有类似的结果。(d)分别验证了微观状态和宏观状态下时间𝑡与平均扩散长度𝐿的标度关系。

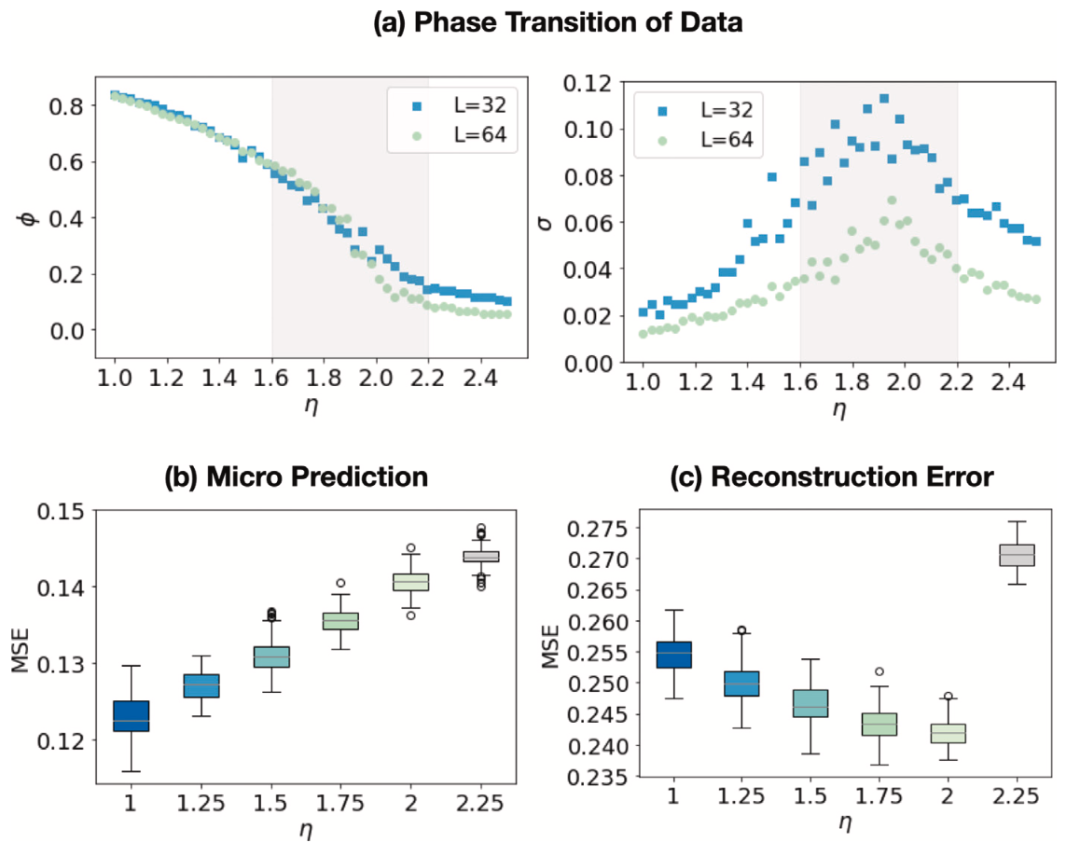
图 4. vicsek模型结果。(a)为序参数Φ（左），其标准差（右）在𝐿= 32和64中随噪声强度η的变化。从图中我们可以粗略估计临界区域在η= 1.6 ~ 2.2的范围内。(b)为五种不同动力学学习器的MSE。(c)为粗粒度学习器的解码器MSE。

意义与展望：迈向自动化的动力学重整化

该框架的突破在于将自相似性作为显式约束，首次实现了数据驱动的动力学重整化。其意义不仅在于跨尺度建模的效率提升，更揭示了复杂系统在参数空间中的固定点行为，为临界现象研究提供了新工具。

未来，这一框架或可结合有效信息（Effective Information）理论，进一步量化动力学的因果涌现强度。此外，其在湍流、等离子体等非平衡系统中也具有一定的应用潜力，未来将推动物理与机器学习更深的交叉融合。

彭晨 | 编译

复杂网络动力学读书会

集智俱乐部联合合肥工业大学物理系教授李明、同济大学副教授张毅超、北京师范大学特聘副研究员史贵元与在读博士生邱仲普、张章共同发起「复杂网络动力学」读书会。本次读书会将探讨：同步相变的临界性、如何普适地刻画多稳态与临界点、如何识别并预测临界转变、如何通过局部干预来调控系统保持或回到期望稳态、爆炸逾渗临界行为的关键特征、不同类型的级联过程对逾渗相变的影响有何异同、高阶相互作用的影响能否等效为若干简单机制的叠加、如何有效地促进人类个体间的合作等问题。

读书会计划从3月7日开始，每周五晚19:30-21:30进行，持续8-10周。诚挚邀请领域内研究者、寻求跨领域融合的研究者加入，共同探讨。

详情请见：复杂网络上的自组织与集体行为：从扩散、相变到博弈 | 读书会启动

集智科学研究中心

集智科学研究中心是门头沟民政局批准成立、门头沟科信局主管的民办非企业，致力于营造跨学科探索小生境，催化复杂性科学新理论。集智研究中心长期关注复杂科学中的核心问题，如涌现、因果、自指、意识、生命起源等等，并充分结合人工智能机器学习技术尝试解决这些问题。目前已有15篇文章发表于国际期刊，其中包括一篇因果涌现的综述和一篇生命起源的综述。这里的文章大部分产生于集智社区读书会。

部分研究成果报道：

• Nat.Commun.前沿：变分自回归网络求解非平衡态统计力学和动力学相变
  

• 如何让机器识别涌现？基于数据驱动的多尺度因果涌现框架

• 合成人造生命的理论视角：从生命起源中学习

• 复杂系统的逆向工程——通过时间序列重构复杂网络和动力学

• 集智科学研究中心重磅综述：复杂系统中的因果和涌现
  

• “涌现”发现之旅：人工智能观察者与涌现的量化｜集智科学研究中心NSR最新成果

访问集智科学研究中心网站了解详情：www.research.swarma.org/research

6. 探索者计划 | 集智俱乐部2025内容团队招募（全职&兼职）