南京研读营“?”合影

编者按：

2019年1月14日-1月23日，由集智俱乐部、腾讯研究院、南京大学新闻传播学院举办了以“计算社会科学：当社会科学遇到人工智能”为主题的系列研讨活动，包括为期5天的计算传播+人工智能研讨班和为期6天的“集智-腾讯”计算社会科学研读营。本文是对4天计算社会科学研读营内容的系统回顾。

1. NN(神经网络)

人工神经网络（Artificial Neural Network，即ANN ），它从信息处理角度对人脑神经元网络进行抽象，按不同的连接方式组成不同的网络进行计算，在工程与学术界也常直接简称为神经网络或类神经网络。大多数情况下人工神经网络能在外界信息的基础上改变内部结构（网络的中参数），是一种自适应系统，通俗的讲就是具备学习功能。[1]

集智相关推文：

图网络重磅综述：基于图的深度学习方法

图网络有望引领下一次AI革命

图网络：悄然兴起的深度学习新浪潮 | AI&Society

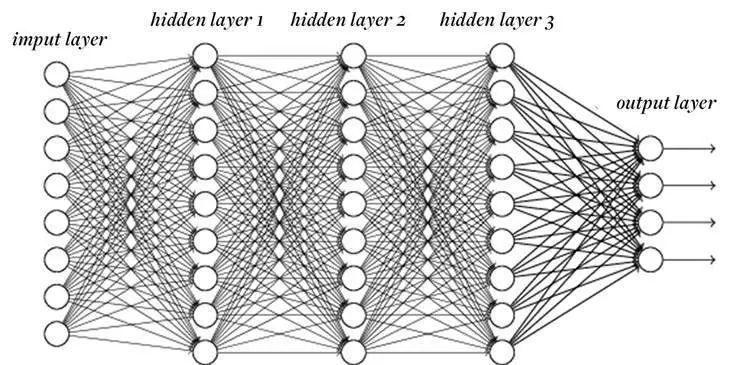
一个有三层隐藏层的全连接神经网络结构示意图。它由输入层-隐层-输出层三部分组成

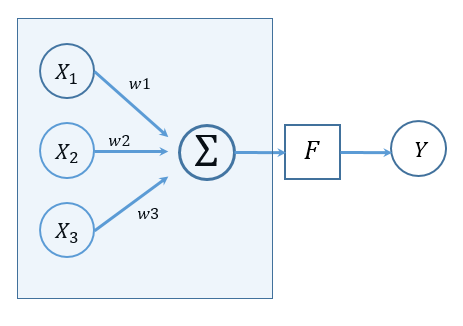
神经网络由基本的功能单元神经元组成，以单个神经元为例，我们看到它实际上在做这样的一个操作，对输入数据X进行加权求和，再利用传递函数F (某种非线性函数)，输出数据。

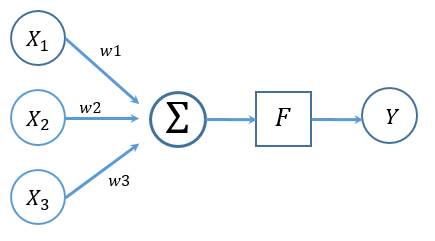
单个神经元的示意图

那么单个神经元的学习过程就是寻找最好的加权方式来最大化对输出Y的期望（在这个部分，对期望最大化的理解是最小化损失函数）。

我们可以把这个神经元做计算的过程写成下面的式子

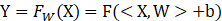
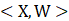表示向量X和向量W内积，在这个是加权求和（或者回归）的意思。F表示某一种激活函数, 这里的b是偏置，可以理解为为了达成目标而做出的调整。

那么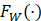，用来表示一个神经元的作用。

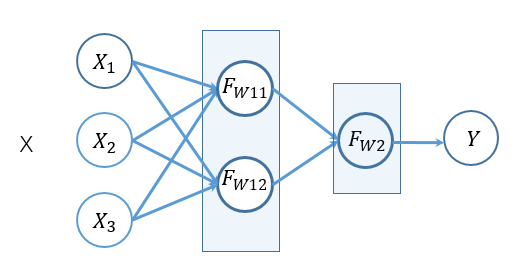
当我们把这个放到一个两层的神经元模型上去看这件事情，实际上它做的就是把输入X(0)做了如下操作：

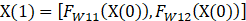
这个过程中，它做了类似核函数分解的过程，也就是，当完成训练以后，每一个神经元被训练出可以看到数据的一部分特征，或者回归出来数据的一部分特征。多个神经元从不同角度来回归信息特征。然后下一层的神经元对提取出来的特征X(1)，再做一次回归，拟合观测数据Y。

激活函数F

常见的激活函数有ReLu、Sigmoid、tanh函数等，现在在隐层中常见的激活函数是ReLu激活函数。

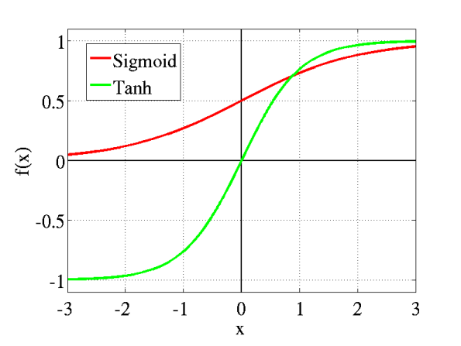
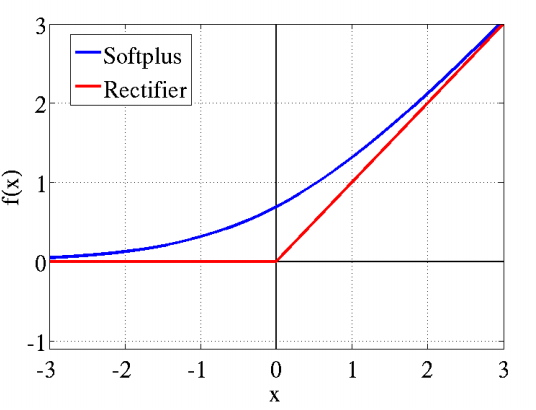
我们以ReLu为例，

f(x)=max(0,x)

实际上它做的是事情是正向激励。也就是说，它相当于把负向的信息过滤掉，只激励正向的信息学习。从计算上来看，简单粗暴，将计算复杂度降低，并且把提取到的一些近乎为0的信息过滤掉，进而能产生稀疏数据，可以加快学习。

2. CNN(卷积神经网络)

我们日常中的很一部分信号是以图像的形式存在的，意味着这一类的数据是有位置结构关系的。对于卷积层的一个神经元，他实际上在是对输入图像和滤波矩阵（对应一个神经元）做内积，也就是所谓的卷积操作，也是卷积神经网络( Convolutional Neural Network，CNN )的名字来源。

如下图[3]：

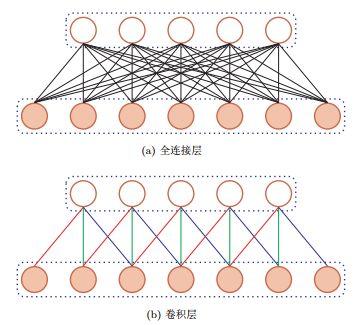
全连接层与卷积层的对比（（b）中所有的同颜色连接上的权重是相同的，橘红色圆圈表示上一层输入）

相较于全连接网络（a），(b)中的5个神经元实际上参数完全一致，只是与输入的连接方式不一样。我们以下图为例，描述一个卷积核的操作：最左边的矩阵是5*5像素矩阵边缘补零后的7*7矩阵，一个中间的3*3矩阵时一个神经元对应的滤波矩阵，通过与像素矩阵中的每个元素为中心的与滤波矩阵同等大小的矩阵对应相乘求和之后得到数值-8，这样，我们能得到一个的5*5的矩阵，与原来的像素矩阵大小相同。

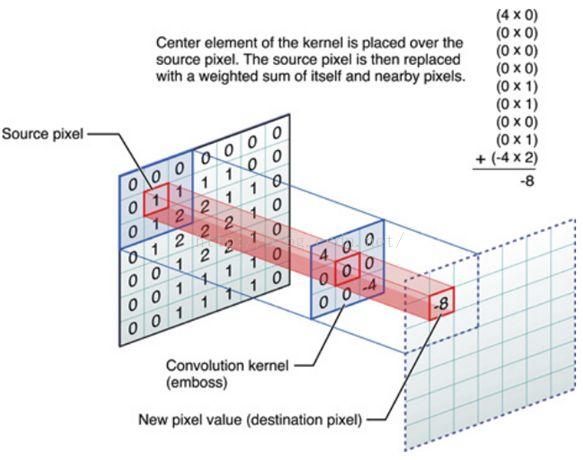
这样，每一个卷积核都可以通过这种方式提取出特征，利用多个卷积核，提取出特征。如果把这些特征直接接入到一个全连接层，就可以构成一层卷积层+一层全连接层的神经网络模型了。

我们可以把这种操作推广到N层卷积层去，卷积层以显著减少网络中连接的数量著称，但特征映射组中的神经元个数并没有显著减少。例如，一个5*5的像素矩阵，经过一次卷积操作后，还是一个5*5的矩阵。如果后面接一个分类器，分类器的输入维数（25）依然很高，很容易出现过拟合。

为了解决这个问题，可以在卷积层之后加上一个汇聚层（pooling），从而降低特征维数，避免过拟合。汇聚层主要的作用是下采样，通过去掉Feature Map中不重要的样本，进一步减少参数数量。汇聚的方法很多，最常用的是Max Pooling。Max Pooling实际上就是在n*n的样本中取最大值，作为采样后的样本值。下图就是一个Max Pooling的例子。

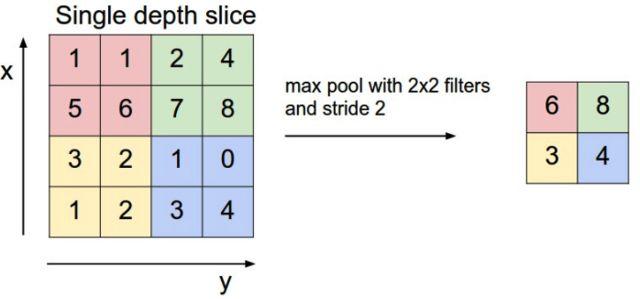
除了Max Pooling还有 Mean Pooling，就是取各个样本的均值。下图就是一个完整的卷积神经网络，一层卷积层+一层汇聚层+一层卷积层+一层汇聚层+一层全连接层+输出层。

整个过程如果忽略激活函数的话，就是通过卷积层提取数据在空间上的特征，利用汇聚层降低低特征维度，然后利用全连接层对这些特征进行回归。

卷积神经网络的一个卷积核就像是用拿着一个放大镜局部地一个一个去看一幅画，提取画里的特征。汇聚层就像是发现在近处看，看到的信息太少，需要把画拿远一点再看。当我们反复这样做，看得差不多了（把特征归纳得差不多了），就可以用全连接层汇总一下提取的特征，归纳总结一下这幅画到底在画的是什么。

3. GCN(图卷积神经网络)

当我们的数据是完全没有结构的数据时，我们只能利用全连接网络来训练数据，当我们的数据在结构上有规则特征的时候，我们可以考虑利用卷积层共享权值的方式来计算，那如果我们的数据是结构化的数据，但并不规则，又该怎么办呢？

图神经网络GNN( Graph Neural Network )应运而生。

它是一类用来处理图（Graph）数据结构输入的一类神经网络。其实图像也是一种图形结构，它是一类具有欧几里得结构的图结构，每个节点与周围的四个节点连接。同时时间信号是类似的数据，只与周围的两个信号数据连接。

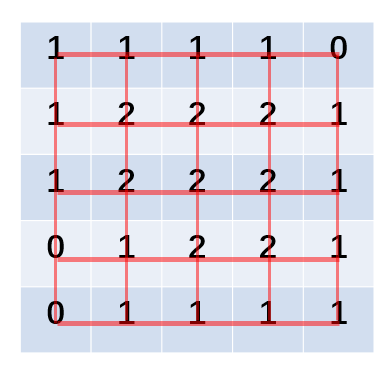
而对于下图中图结构的数据来说，则要比上面的数据复杂得多，一个节点既可能与4个节点产生连接，又可能与2个节点产生连接，这种连接方式对于每个点可能是不一样的。

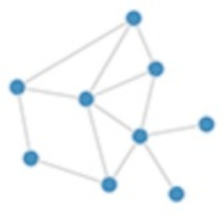
对于一个图G=(V,E)来说，V是它得节点，每个结点有各自的特征，E表示图上的边组成的集合，表征了图的结构，可以用图的邻接矩阵A表示。我们的目的，是通过利用图的节点自身的特征以及图的结构特征来完成相应任务。

那么，对于图结构的数据，我们实际上的输入是节点的初始特征以及节点与节点之间的连接关系（连接矩阵），期望输出的是图上节点的标签或者图的标签等等。

对于原始的图卷积神经网络来说，它完成的任务是，给定图上某些节点的标签，去反推其他节点的标签信息。

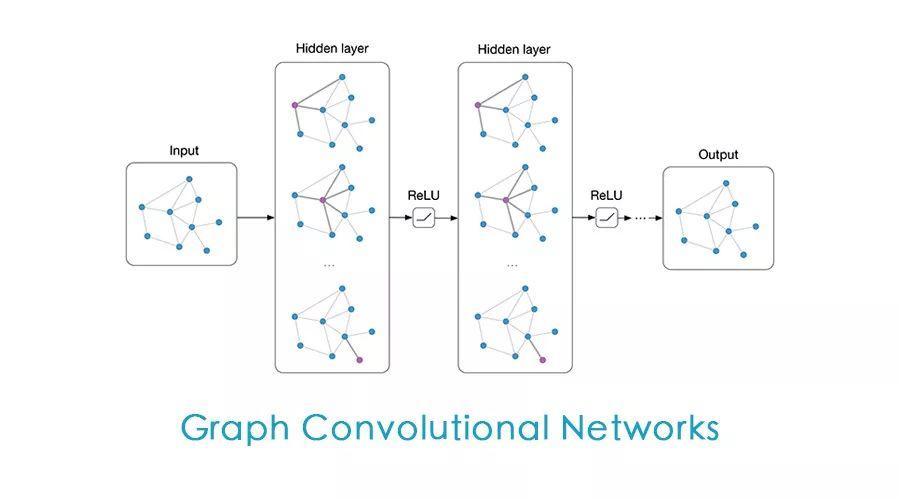
回顾卷积神经网络，卷积层中，对一个5*5的像素矩阵，每一个卷积核（以3*3的卷积核为例）对应着5*5个参数共享的神经元，每个神经元除了连接自己所对应的像素点之外，还和这个像素点周围的8个像素点连接。那么在图结构上，我们其实也是给每一个节点分配了一个神经元，只不过在GCN中这些神经元的权重不会改变，每个节点i的加权方式是这样的：

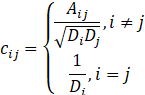
其中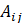=1，表示i, j有连边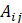，=0 ，表示i，j没有连边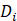，表示节点i的连边数目（邻居数目）。

对于一个图卷积层，更新过程如下：

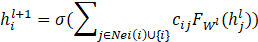
它其实由两个中间过程构成：

利用全连接网络对上一层信息进行特征降维度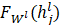，或者说特征提取（embedding）。
利用图结构快速传播局部信息（投票机制），加速学习特征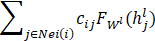最后，利用激活函数输出提取的特征。

这里的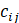是提到的加权求和的方式。

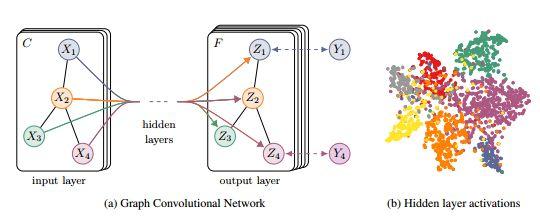
在Thomas N. Kipf等人的实验[4]中发现，相比其他模型，利用图结构，可以快速有效的完成任务，并且有很高的准确率。

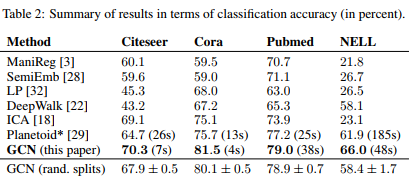
值得一提的是，在Kipf等人提出该模型之前，有很多处理GNN的方式。比如利用图谱分解来处理处理图结构信号，也有利用节点邻居采样的方式限制每次处理的邻居数，也有利用随机游走构造时间序列在利用word2vec的方法。

这些方法要么是严重依赖采样方式来提取用全局信息，不确定性很大，要么是利用复杂的数学技巧提取图谱特征，这个需要利用图的全部信息，计算复杂度很高。而GCN的处理方式则要简洁很多。

4. GAT(图注意力网络)

GCN中的投票是一种等权投票的模型，而图注意力网络（ Graph Attention Network，GAT ）利用注意力机制提出来一种不等权的投票机制。

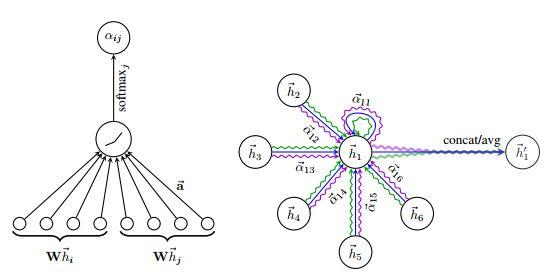
投票的权重是按照一种叫做注意力机制的方式来实现的。

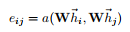
它通过训练一个全连接神经网络来学习前者对后者信息的关注度，然后进行下述归一化的方式赋权。

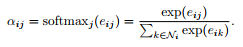
这里的就是我们学习到的投票权重。

在GAT中，它采用了多头注意的机制，实际上就是按照我们之前提到的，是一种把注意力函数进行核分解的方式，分解成若干个注意力头（attention-head）然后综合每一个注意力头的信息得到节点i对节点j的注意力。

5. 图神经网络可以

帮助我们思考哪些问题？

在几天的研读营的活动中，我们以图网络为核心，分享和梳理了常见的几种神经网络模型。其实，在我们日常的研究中，有很多问题都可以表述成一个网络问题。除了去做网络的社团检测，还有一系列问题可以用GNN的框架研究问题。

例如，用户推荐问题，给定用户-产品的关系，给定用户，推断用户会购买哪些产品。又比如说联络预测问题，给定网络结构，预测连边。再比如，给定网络结构（或时序上的结构），推断网络的类型，预测网络的演化，学习网络上的动力学（流行病转播）等等。

同时，GNN网络还有可能帮助我们预测系统结构，学习图像中的语义关系，学习关系推理，预测蛋白质的特性等等。

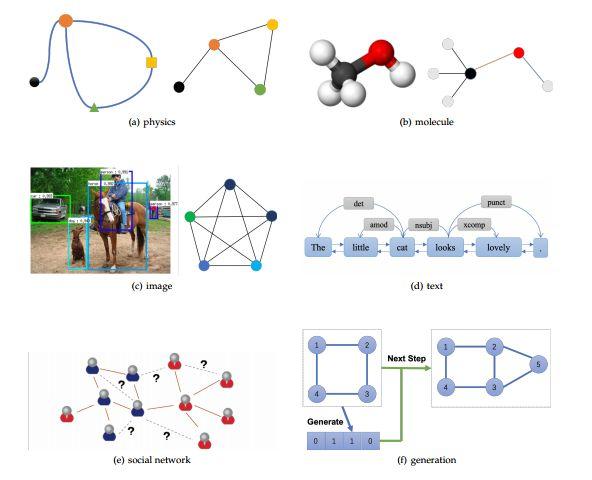
网络结构的信息往往蕴含着大量的与功能相关的信息。现实中，绝大部分的大型网络是具有稀疏结构的，利用大型网络的这种特性，可以帮助我们更快速地根据数据训练模型。

参考资料

https://zh.wikipedia.org/wiki/人工神经网络
Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks. NIPS. 2012: 1097-1105.
https://nndl.github.io/chap-卷积神经网络.pdf
https://arxiv.org/pdf/1609.02907.pdf
https://arxiv.org/pdf/1812.08434.pdf

Graph Neural Networks: A Review of Methods and Applications