meme卡片集 | ©marble.cards

导语

模因（meme，又译作觅母、迷因），俗称“梗”，是指基因一样依赖宿主、复制传播的“文化基因”。今年的一篇论文，构建了模因在网络上传播的动力学模型，本文将详细介绍这项工作。

目录

1 传统疾病传播的模型概述

2 模因是怎样传播的

3 模因传播的基础模型

4 模因的传播的混合通用模型

5 用于验证数据集概述

6 参数拟合

7 预测模因的流行

8 和疾病模型的对比

自从在《自私的基因》中第一次亮相，模因（meme）这个概念一步步地把它自身变成了广为传播的模因。与生物学的基因相比，模因指的是文化传播中具有固定功能的一个组件。正如侯世达所言，它如同在大脑之间跳跃着的火花一样引人注意又能够传播。比如艺术中的哥特式风格，电影分类中的僵尸片。在社交网络上，模因可以是一个观点，对某电视剧的追捧，或者是一个突然流行起来的Emoji、流行语。

以往关于网络上的信息传播研究最多的话题是疾病的传播，然而模因在社交网络上的传播因其背后机制的不同，而呈现出不同的规律。2019年2月在arxiv.org发布的一篇预印本论文，为模因传播创建了数学模型，并在豆瓣、微博等数据集上验证了模型预测准确性。本文将以这篇论文为背景，为读者介绍模因传播背后的规律。

论文题目：

A model for meme popularity growth in social networking systems based on biological principle and human interest dynamics

论文地址：

https://arxiv.org/abs/1902.00533

1 传统的疾病传播模型

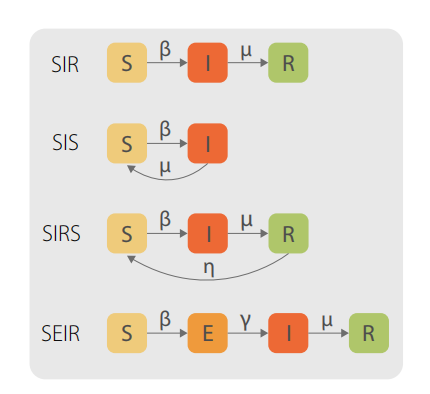
图1：图示四种疾病传播模型。

S-易感人群（Susceptible）

I-已感染的人群（Infectious）

E-暴露在抗原环境的人群（Exposed）

R-恢复带抗体人群（Recovered）

已有的疾病传播模型可以为我们研究模因的传播提供灵感与工具。图1从简单到复杂，一步步展现了如何对疾病传播的过程进行建模。图中的S是易感人群（Susceptible）,代表一共有多少人可能会被感染。其中有β%的人感染（Infected），之后有μ%的人被治愈，治愈者有了抗体，不再感染，这是SIR模型描述的情况。而如果全部的人都能治愈，那就是SIS模型，而如果患病后的人有一定几率抗体消失，重新进入易感人群，那这就属于SIRS模型，而SEIR模型在SIR模型基础上加上了暴露（Expose）这一步，用来描述不是所有易感人群都会暴露在接触病毒的环境中。

在上述的疾病模型下，人群中曾经感染过病毒的人的比例会呈现如图2所示的趋势。最初是疾病随机、小规模地爆发和消退，之后有一个指数化增长的阶段，之后在SIS模型中，大部人都感染过，例如流感病毒这样的最终会康复的病毒；而在SIR模型中，指数化增长后，随着越来越多的人获得抗体，感染病毒的人会逐渐回到0点，例如人类最终通过疫苗消灭了天花病毒。

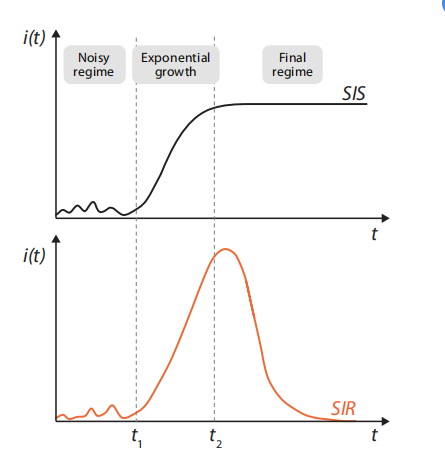
图2：SIS 和 SIR模型感染个体随时间变化示意图 | © Epidemic processes in complex networks

2 模因的传播有何不同之处

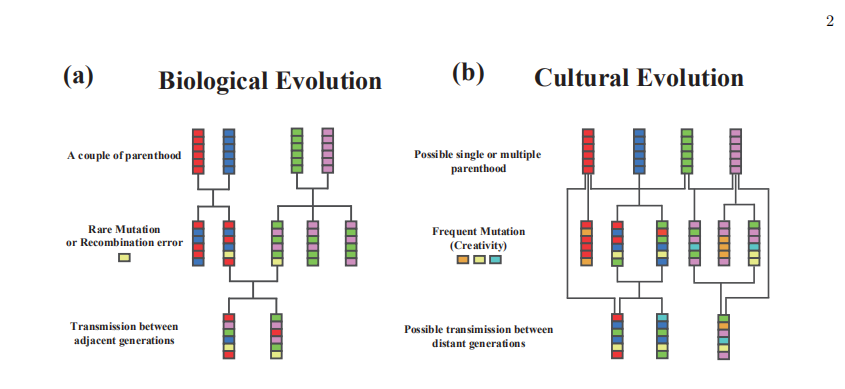
图3：模因与基因进化传播的区别

论文题目：

Evolutionary Dynamics of Cultural Memes and Application to Massive Movie Data

论文地址：

https://arxiv.org/abs/1903.02197?context=physics.soc-ph

图3来自今年5月发表的论文，该文关注的是模因的进化动力学及其在电影风格上的应用，这里借用过来说明模因与基因进化的三点不同之处：

任何一个模因的“父辈”会有一个或者多个，而不是只有两个；
模因的变异不是来自于罕见的点突变或者仅仅是父辈之间重组，而是持续的大规模的改变；
模因的传播可以跨越父辈的中间层，直接从第一代传播到第三代。

这三点说明模因的进化，更像是微生物的进化，可以有横向的基因交流，一种菌可以直接从另一种菌那里“借”到有用的基因片段。

由于模因的进化更类似微生物，因此对模因流行程度的建模，也应优先借鉴已有的对微生物群落建模。由于关注考虑的是模因的传播和流行，因此之后的模型中不涉及模因本身的改变，这里一番解释，是为了让不熟悉的模因的读者能对这个概念有一些直观的理解，模因能复制，能传播，也能进化。

3 模因传播过程中的三个状态

用微生物的进化过程，来仿生模拟迷因的传播，从而构建起和疾病传播不同的基础模型，下面将对其进行详解。

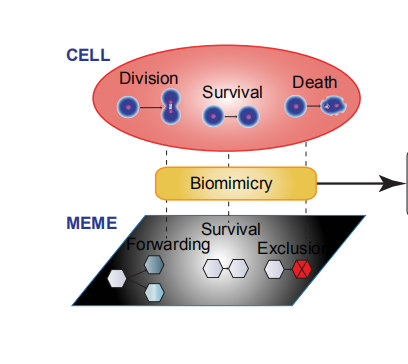
图4：细胞的生活周期与模因的生活周期对比

上图是一个从微生物“传播”模型到模因传播模型仿生过程的示意图，红色描述细菌群落的演化，细菌分裂为多个细胞，之后部分细胞存活，部分细胞死去。而对于模因，例如一则谣言、对某电视剧的推荐，也是最初由最初一小群人转发，之后部分人被成功传播，部分人则无法被该模因影响（exclusion）。

以一个7个人的群体为例，图5和图6展示了M1、M2、M3、M4这4个模因是如何在他们之间传播的。

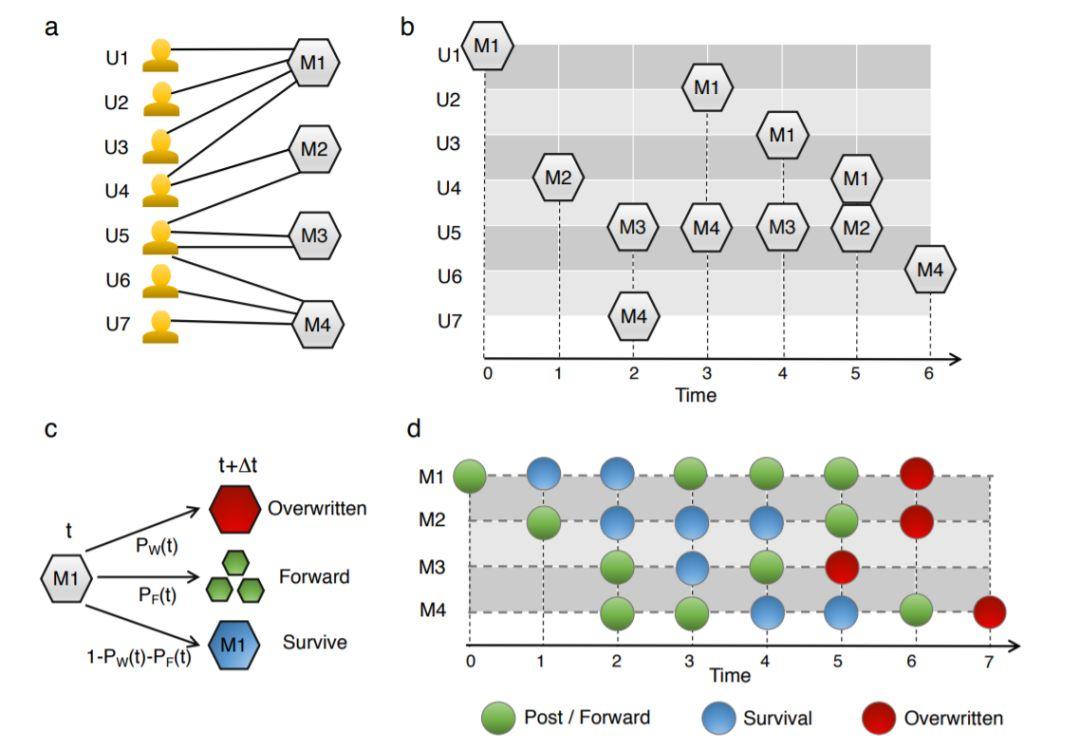
图5：模因传播图解

图5b展示的是4个模因在7个用户身上存活生命周期的间轴，a展示的是模因1-4在这个模拟的时间段内分别影响了哪些用户。图b是图a具体细节的描述，其中六边形是代表用户传播模因这一行为。

如图5c所示，针对每个模因，有三种可能性。这个人要么在下一时刻以PF的概率传播这一模因，要么以PW否认该模因了，而这两种状态之外剩下的概率里，该人仍旧相信该模因，但是并不传播它。d图与b图都描述了模因的状态，只不过是从用户的角度切换成了模因自身生存的角度。图d展示了上面4个模因随着时间流逝在7个用户心中的总状态，这张图可以类比微生物模型中的分裂，生存与死亡。

4 在模因传播中

引入社交网络的影响

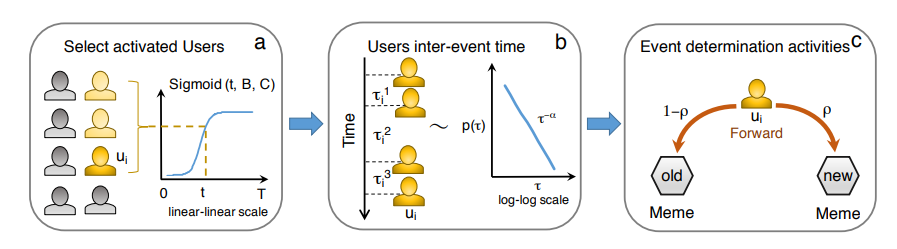
图6：模因在社交网络上的传播

上述基于单体模型（Agent-based model）构成的只是基础模型，没有考虑社交网络中人际互动影响，只有进一步添加对网络动力学建模，才能构建用来预测模因流行程度的混合通用模型。如图6所示，研究者考虑群体之间相隔影响，提出了模因传播的3条基本假设：

将一个用户被一个模因影响，比如读到某本书，这个过程称之为激活。这个人被激活的概率随着身边已激活的人的比例呈Sigmoid函数分布。形象的说，就是朋友圈最初只有几个人追一部剧的时候，被种草很难，之后随着比例增加，概率速度提升，等人多了之后，用户已经全部覆盖，这时候模因的传播进入了平台期。（左图所示）

用户两次活跃时间的间隔，呈幂律分布，也就是对某位用户，其在20%时间段中异常活跃，参与了的传播或者接收模因行动数占总数的80%（数字用来打比方），而剩下的时间里，基本不会参与模因的传播。

用户在传播模因时，有一定几率p传播之前收到的模因，在1-p的概率下转播旧的模因。

这三条假设中，最重要的是第一条，该条描述了人际交往对模因传播的影响呈非线性的增长。而Sigmoid函数是最常用的描述非线性增长的函数。在该模型中，用到了sigmoid函数的变种

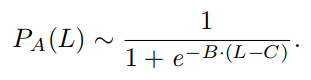
公式1：改进的Sigmoid函数

从数学上来看，针对某模型，特定的参数B和C分别决定了函数的陡峭程度，以及在横轴上偏移的数值。从模型现实意义上来看，可以形象地理解为：B是传播时间的“衰减率”，该值越小，模因达到传播速度最高点所需的时间相对越长。该数值越大，模因传播模式越趋近于爆发式增长；当时间达到C点时，模因的传播速度达到最快，模因正处于传播速度的顶峰。C值越大，模因需要越长的时间来酝酿，C值越小，爆点来得越早。

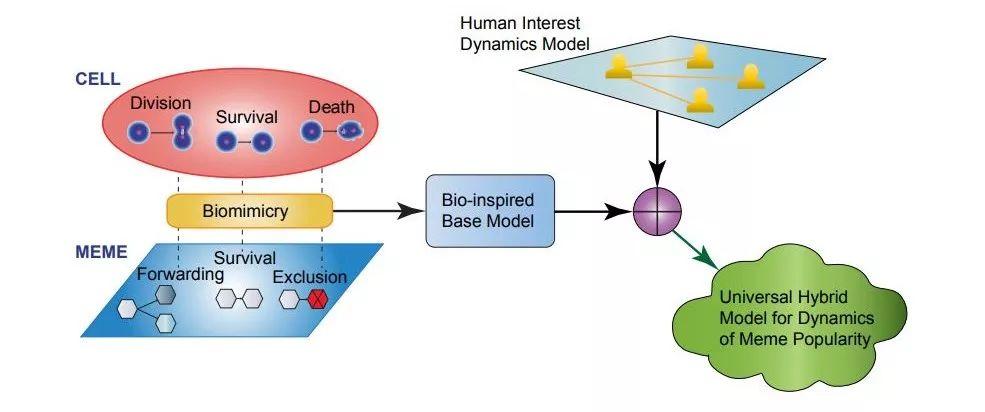
图7：模型的建模全过程示意

5 模因在具体数据中的表现形式

在这篇预印本论文中，用到了3种不同类型的数据集，分别是美食推荐网站delicious、豆瓣读书、电影和音乐、以及微博上的转发数据。对于美食网站，收藏一家餐馆算做是传播模因；对于豆瓣，对书/电影/音乐评分算是传播模因；而微博上的转发算是模因的传播。对于一本书、一部电影、一张专辑，如果在某个时刻后不再被提及，那相当于该模因被新的模因覆盖掉了。

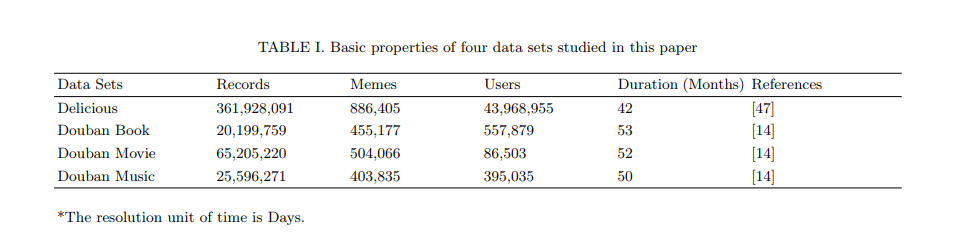
表1：数据集的基本性质

上表说明了使用的数据集的大小和特征。对于不同持续时间的数据集，研究者为了分析方便，对其进行了归一化。该数据集中最令人意外的就是用户数：豆瓣电影的用户数比读书和音乐少了一个数量级，而其模因数目，也就是包含的电影数目却是最多的，并且，电影的记录数目也是最多的，这说明豆瓣电影用户更多是重度用户。而在delicious网站上，用户数目比豆瓣用户数高了2个数量级，网络中传播的模因数目却在相近的水平。这说明这些数据集不仅是内容不同，网络的结构（例如稀疏程度）也有所不同。

6 从真实数据中预估模型参数

有了模型和数据，接下来要做的是从真实数据中去拟合模型中的参数。下表给出了不同数据集拟合出的参数。

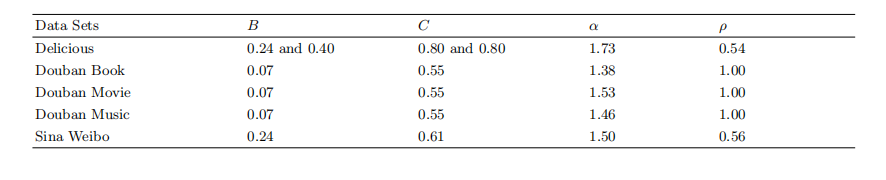
表2：模型训练后的参数

这里美食网站有收藏一家餐馆，以及将该餐馆移除收藏两个操作，因此其对应的B和C有两个。先看α与ρ，它们是决定用户分享频率和优先级的参数，其中假设转发时间间隔是幂率分布的，α是幂率函数中的唯一参数，α越大转发越频繁，而ρ是人们转发新消息的概率，ρ越接近于1，人们越倾向于传播新信息。

民以食为天。美食网站的用户、平均两次活跃之间的间隔是所有网站间最小的。豆瓣电影都是些重度用户，活跃时间的间隔次之。而读书所需的时间较长，用户活跃的时间间隔也是相对最大的，这符合预期。

另一个有趣的发现是：豆瓣系的网站，其拟合出的B和C都是相近的，也就是说，不管是电影、图书还是音乐，艺术文学作品背后模因的扩散方式平均来讲都是以相对平缓的方式进行的。

最让人意外的是微博和美食网站的拟合出的B都是0.24，意为美食网站和微博上模因的传播更具爆发性，美食与短消息更具吸引力，更容易让人们进行传播。微博是虽然也有部分网红餐饮成分，但其主流是以娱乐资讯为代表的实时新闻。两者的引爆点相同，也许这能用进化心理学解释，人们评价新闻是否值得转发，和评价食物的好坏，背后有着相似的动力。美食网站有将餐厅移出收藏这个选项，该数据拟合的B、C值分别是0.4和0.8也就是反过来，当人们开始对一家餐厅失去兴趣的时候，它会以更快的速度被抛弃。

从这里引申到社交网络中，可以知道，当一个社交网络中遇到的50%左右的用户都在传播伪科学、假新闻等无效信息时，那这个社交媒体会开始迅速流失用户，从最早的天涯，到后来的人人网莫不如此。

7 模型预测的结果及其启示

图8：模因流行度预测

图8中的横轴是正则化后的时间，纵轴是某个模因还有多少流行的潜力。P等于1的时候，意味着在数据集包含的时间内，模因的传播和用户的流出达到了平衡。图中不管是黑色虚线代表的模拟结果，还是理论推算出的蓝色虚线，按照数据拟合出的参数，在对Pn的预测上，几乎没有误差。这说明了该模型包含了对模因传播有影响的全部因素，且适用于多种截然不同的网络。

下面是Pn的计算公式，其中的St是某时刻该模因在多少用户中“存活”，Wt是多少人接收到，却没有被该模因影响（overwrite），Ft是多少人在传播模因，Pn的分母为最大值时（逼近1），意味着传播该模因的人最小（逼近0），即该模因已经过气了。

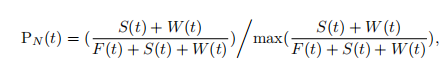
公式2：模因流行度与时间关系计算公式

对比三种不同网络，对于模因的传播的规律，可以比较异同。不管是什么样的内容，所有的模因都会过气，对于文艺作品，其传播是相对线性的，而在微博上，模因的爆发则更加突然。

8 对比疾病传播模型及总结

相比疾病的传播，模因从传播机制上就不是非黑即白的，必须要考虑人的行为——同伴压力（peer pressure）（比如大家都看权力的游戏，我不看显得不合群），也需要考虑人际交往的频率遵照幂律分布。因此不能简单的修改某种疾病传播模型，而需要从微生物群落的繁衍借鉴灵感，同时在网络中引入社交的机制。社交网络由于其内容不同，其数据看起来有明显的差别。但在本文论述的模型下，数据的差异可以通过拟合出的参数不同加以解释，后续再根据参数去预测模因流行的群体统计指标。不同网络可以用相同的模型准确预测，意味着在微观层面，这些网络有着相同的生成机制。虽然无法具体预测一部电影是否会火，但对社交网络的分类问题、网络的鲁棒性、以及网络中模因的管控机制设计有所助益。