技术如何演化:创新背后的数学递归结构

论文题目:
The mathematical structure of innovation
论文地址:
https://arxiv.org/abs/1912.03281
技术的本质是什么?它是如何进化的?
尽管我们熟悉风力涡轮机、触摸屏和 GPS 等各种具体技术,但“新技术究竟如何诞生”对我们来说依然是一个谜。一方面,在传统观念中,人们往往把技术当做科学的附庸,并潜意识认为技术对人类具有某种潜在性的威胁,一方面以往人们对技术的思考大多由哲学家和社会学家们进行,工程师们大多热衷并忙于具体技术细节,无暇顾及。这都导致了人们长期以来将技术本身当做一个外部客观对象,潜藏在一个个具体的“黑箱”中。
正如如果没有基因学说和解剖学研究,就很难厘清物种之间的关系一样,如果不深入到技术内部中去,也很难看清它们是如何相互联系,如何起源以及如何进化的。
著名经济学家、圣塔菲研究所外聘教授布莱恩·阿瑟(Brian Arthur)在《技术的本质》[1]一书中,曾从复杂系统视角对技术本质及进化做出过清晰阐述:
-
所有技术都来自其他次级技术的组合,元初技术是对自然现象及其效应的捕获; -
通过组件模块化和技术集群形成的域,技术进化有一个自下而上的层级递归结构; -
与人类需求互动,技术进化创造并引发经济进化而与人类共生。如果技术让人远离自然,则是危险的,反之人性的技术则给人类带来生命活力与繁荣。
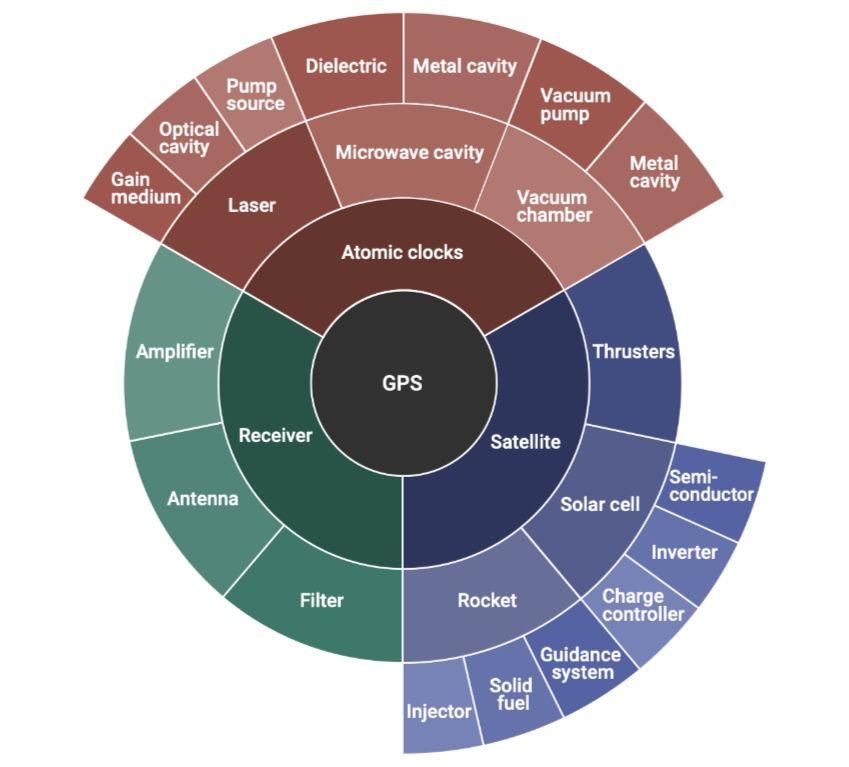
2019 年底,来自伦敦数学科学研究所的两位数学家,在 arxiv 上发布了一篇预印本论文:《The mathematical structure of innovation》,他们对布莱恩·阿瑟的技术理论进行了定量化研究,不仅建立了技术递归创新的数学模型,还推导出了技术递归的预期收益的公式,通过语言、美食与药品三个领域测试研究发现,以最佳配对大小的技术组件作为拓展模块进行重复递归,可以有效提高新技术产生的效率,从 2 倍到 28 倍不等。此外论文中还给出了技术创新过程的解释和实践策略。
组合进化与递归
从布莱恩·阿瑟的技术理论我们可以看到,技术的本质是通过原有技术的组合,对捕获的自然现象有目的地进行编程。
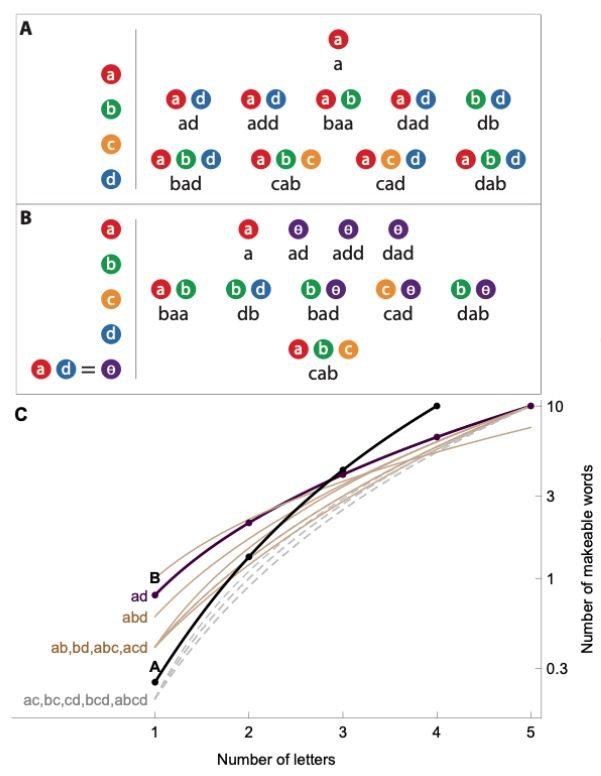
从乐高游戏和字母组成单词例子我们可以看到的,将正确的组件组合转换为新的组件可以大大增加可制造技术的数量,但是将太多的组合转换为组件会产生相反的效果。
技术创新的数学模型
现在来考虑一般技术组合过程。
任何技术都是由次级技术组件组成。这些组件可能是某项基本技术、一个技术组合或技术模块。
对任何技术, 若由 c 个不同组件组成,则称其技术的大小 为 c。组件排列顺序和出现次数无关。例如对单词“ innovation”具有 c = 6 个组件,而不是10 个。
假设上帝的“橱柜”中共有 N 个可能的组件。但在任何现存的技术阶段,人只能取到自己“篮子” n(黑体) 中 n 个组件。则包含 n 个技术组件的篮子n 可得技术数量为 p(n)。
显然,p(n) 大小取决于篮子中的特定组件成分之间的组合,而非能组合的总量。例如从英文字母 abcde 能获取的单词数,要比最后五个字母要更多。即对 n=5 的两个篮子n1和n2,有 p(n1) > p(n2) 。
在篮子中,大小为 c 可制造技术数量用 p(n,c) 表示。例如在 abced 中,目前存在
{cab、bad、bed、cad、dab、deb、ace、bae},故 p(n,c) = 8
此外,研究还定义了技术空间的预期大小以及其中技术大小 c 的情况。前者是从上帝的橱柜 N 中取所有大小为 n 可能篮子能产生技术数的平均值。例如在字母表中 abcde、vwxyz…等都是 n = 5 的字母篮子。后者是所有可能篮子中大小为 c 技术 p(n,c) 的平均值。

c 个随机组件产生技术可能大小
c 个随机组件产生技术可能大小
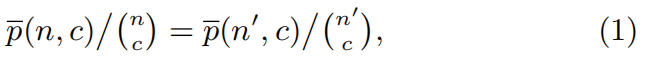
其中分母组合数C(n,c)。两边大小都代表组件数为 c 随机组合成一种技术的可能性大小。
这就是说,假如我们在 26 个英文字母中随机取 5 个字母 4 个字母,那么大小为 c = 3 的单词数的平均值,分别除以二者组合数,两边数值是相等的。
组合可用性与模块
组合可用性与模块

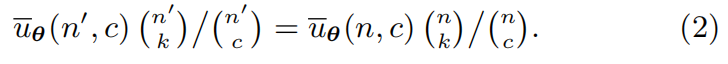
技术递归效应与拓展模块
技术递归效应与拓展模块
有了以上基础,我们现在考虑技术递归过程中技术数量变化情况。
在方程 (1) 中,等式两边均代表两个不同技术阶段 n’ 和 n 中 c 个随机组件产生技术的可能大小。因为作为分母的组合数所以,增加制造新技术的可能,就取决于分子。
现在考虑在技术递归中,用一个 k 个组件组成的模块θ替换原有的技术组合 θ。即 θ → θ,则技术新阶段篮子组件大小有:c + k − 1 → c。例如将 ab = θ,则 abcde 变为 θcde。技术递归的效果取决于替换后的关系网络的变化是积极的还是消极的。
在论文中,研究者们推导出了应用 θ→θ后可以制造的平均预期技术数的公式:
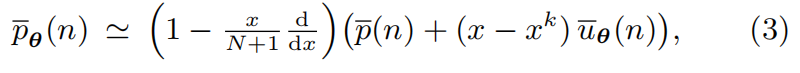
其中 x = n / N(在假定非全知和无偏估计下),当应用模块θ后,即从 N 个组件的原始集合中提取的 n 个组件相比,我们可以从更新的 N + 1 个组件中制作更多的技术,则称增加可制造技术数量的组合θ称为一个扩展模块(Expanding module)。
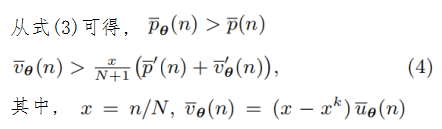
技术递归效应:语言、美食与药品
-
在语言中,技术是 38,970 个英语单词,组件是用来生成它们的 26 个英文字母。 -
在美食中,这些技术是 56,498 种食谱,组件是381 种用来制作的食材和配料。 -
在药品上,所有技术是已知的 1363 种药物治疗配方,其成分是用于制造它们的 901 种单独药物 [25]。

扩展模块的组合很稀有
扩展模块的组合很稀有
拓展模块几乎都是完整技术
拓展模块几乎都是完整技术
技术组合理论的前提假设就是,技术不是从零开始构建的,而是现有技术新组合的结果 [1,7]。也就是说,技术组合本身就该是一项完整的技术,而非单纯部分组件的组合。
研究者们通过进一步计算验证了这个假设。结果很显著,在语言、美食和药物三个领域,几乎所有扩展模块都是完整的技术,分别占全部模块的 98.70%、96.88% 和 98.62%。从图 3 中可以看到,代表二者的红色和紫色曲线几乎是重合的。
持续递归的惊人威力
持续递归的惊人威力
总结:如何发现新技术?
模块化、相邻可能与环境
正确识别模块:
可能性、递归性、完整性
正确识别模块:
可能性、递归性、完整性
转换相邻可能:随机变异、
重新定域、持续递归
转换相邻可能:随机变异、
重新定域、持续递归
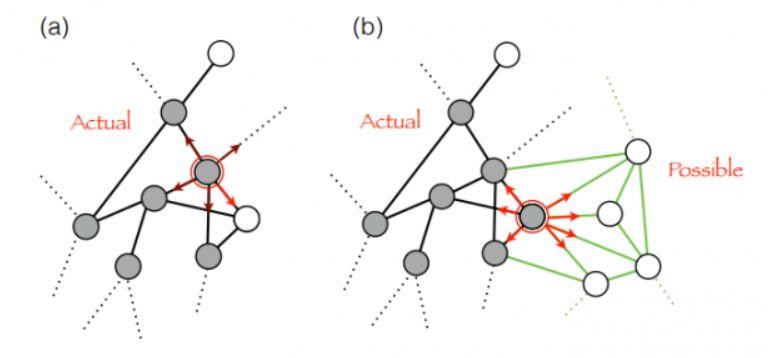
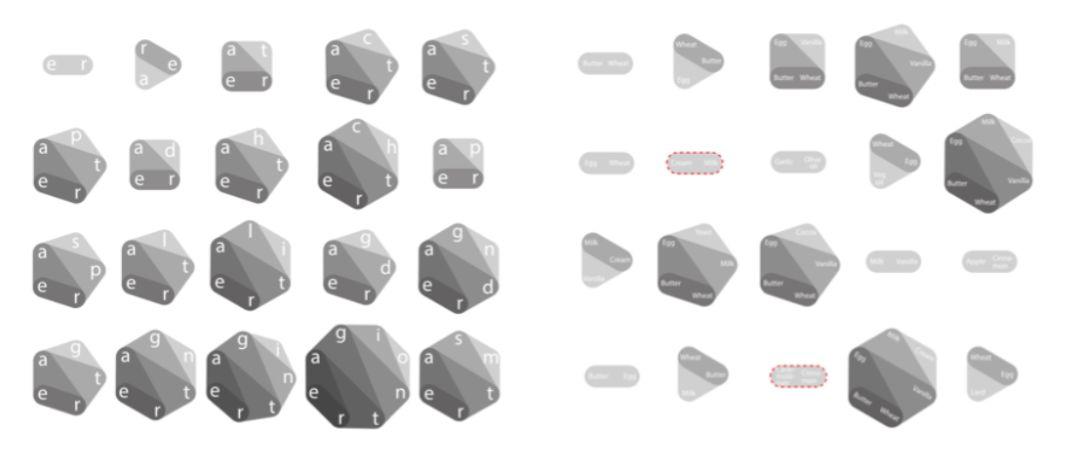 图 6:语言和美食领域模块配对随着持续递归的不断生成
图 6:语言和美食领域模块配对随着持续递归的不断生成
新技术塑造自身环境:
长期不可预测性
新技术塑造自身环境:
长期不可预测性
药品发现:旧药新用
药品发现:旧药新用
作者:十三维 编辑:张爽

【购书赠扑克】技术的本质:技术是什么,它是如何进化的 | 布莱恩·阿瑟

△ 购买《技术的本质》赠送复杂性科学知识卡片△
推荐阅读

集智俱乐部QQ群|877391004
商务合作及投稿转载|swarma@swarma.org
◆ ◆ ◆
搜索公众号:集智俱乐部
加入“没有围墙的研究所”

让苹果砸得更猛烈些吧!
本篇文章来源于微信公众号:集智俱乐部










