图1：由志愿者March提供的分形几何示例


“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

今天分享复杂性科学领域里面一个典型而有趣的模型：分形几何。本文将展现分形的基本概念，典型案例，知名学者、和一些入门的学习资源。

我们知道直线是1维的，平面是2维的，空间是3维的，时空是4维的，那身体的毛细血管、绵延的海岸线、晶莹的雪花这些不规则的几何体，又是多少维呢？透过分形几何的理论，我们可以了解如何计算这些非规则的曲线的豪斯多夫维度（即分数维度）。并且运用这种思维去理解生活中那些平常但是却在细小之处变化的现象，加深你对这个复杂世界的认识。



目录


一、什么是分形几何？

二、分形几何的重要概念

三、分型几何的几个典型示例

四、相关资源推荐

五、集智百科词条志愿者招募


1、什么是分形几何？

分形几何学，就是一门以不规则形态为研究对象的几何学。分形最大的特性是具有自相似性，不管是放大或者缩小研究对象，你都会看到局部和整体具有相似的结构。因为分形几何的研究对象普遍存在于大自然中，例如我们熟知的雪花、树叶、群山、云朵、海浪等等，所以分形几何学，又被称为是“大自然的几何学”。

但同时分形在现实生活中有广泛的应用，包括在动画制作，3D建模、疾病监测、股票市场以及通信等领域。分形第一次应用的电影是《星际迷航2-可汗之怒》，计算机科学家Loren Carpenter从一个全景图出发， 由一些非常粗略的三角形构成，然后对于每个三角形，分成4个小三角形，继续这样操作下去，迭代，形成了非常逼真的山脉。


推荐视频：【PBS纪录片】寻找隐藏的维度【中英双字】:

https://www.bilibili.com/video/av13766486?p=1


2.分形的重要概念

 

自相似性(Self-similarity)


自相似是指局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似性，比如树干和枝桠的自相似，大的旋涡和小旋涡的自相似等等。


无标度性（Scale-free）


所谓无标度性，是指当我们变换不同的尺度，都会发现系统还是那样，它没有变化（即自相似性），也就是标度不变性。比如我们所说的大漩涡套着小旋涡，它们发生在不同的尺度，但是却表现出相似性，这就称为无标度特性。


非线性（Nonlinear）


非线性就是和线性相对，线性是指成比例，而非线性则指输入和输出不成比例，比如抛物线就是非线性的。在复杂系统中，非线性是最重要的特性之一。


图2：来源于Dave Whyte
 
无边的奇迹源自简单规则的无限重复。

——分形之父  Benoit B. Mandelbrot


3.分形的几个典型示例


康托尔集（Cantor set）


分形的起源是康托尔集（Cantor set）。我们取一个线段，把它中间的1/3去掉得到两个分开的线段，再对剩下的两段进行相同的操作，得到4个线段，这样重复进行下去直到无穷，最后得到的图形集合就是康托尔集。



图3：康托尔集（Cantor set）的一部分 形似道家的卦图


Mandelbrot 集


提到分形，我们就不得不提曼德布洛特集合（Mandelbrot set），这是一种在复平面上组成分形的点的集合，以数学家伯努·瓦曼德布洛特（Benoît B. Mandelbrot）的名字命名。Mandelbrot集合与Julia集合有些相似的地方，例如他们都使用相同的复二次多项式来进行迭代。

曼德布洛特集合可以用复二次多项式：。曼德布洛特集主要是通过固定z0=0，不断迭代c得到的，产生一组发散数列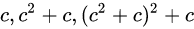：如果数列发散，则在二维平面内，将所有不属于集合内的点标记为黑色，属于集合内的点按照发散速度赋予不同的颜色，就可以得到经典的曼德布洛特集图像。



图4：The Mandelbrot set


Julia集


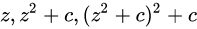Julia集和 Mandelbrot 集具有相同的数学表示形式，唯一的不同是，Julia集是通过固定c，不断迭代，计算z的值得到的，产生一组发散序列同理，将所有不属于集合内的点标记为黑色，属于 集合内的点按照发散速度赋予不同的颜色，会得到不同的Julia集图像。


图5：当c取某一值的时候Julia集合在复平面上的图像


科赫曲线 Koch curve


科赫曲线（Koch curve）是一种神奇的曲线，因为形态跟雪花很像，所以也称为科赫雪花，最早出现在海里格·冯·科赫（Helge von Koch）的论文中，通过下面这个动图，你知道科赫雪花是如何形成的吗？


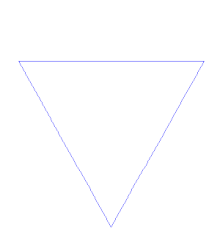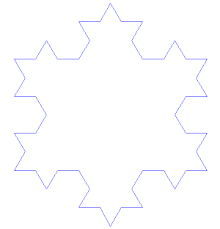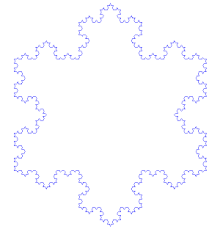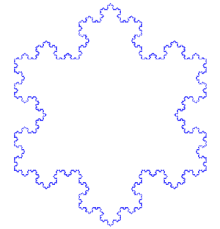
第一步：画一个等边三角形，并把每一边三等分；

第二步：取三等分后的一边中间一段为边向外作正三角形，并把这“与主三角形靠近的一边”擦掉；

第三步：重复上述步骤，画出更小的三角形；

第四步：一直重复。


由上述步骤所画出的曲线叫做科赫曲线（Koch curve）。


谢尔宾斯基三角形 Sierpinski triangle


我们都知道一个平面三角形的维度是二维的，但是在分形几何中，三角形有不同的维度计算方法。谢尔宾斯基三角形（Sierpinski triangle）也是一种分形典型示例，由波兰数学家谢尔宾斯基于1915年提出。它是自相似集的例子。它的豪斯多夫维数是可以通过多种方法得到这个三角形，这里介绍其中的一种方法：


第一步：取一个实心的三角形。(多数情况下使用等边三角形）；
第二步：沿三边中点的连线，将它分成四个小三角形；
第三步：去掉中间的那一个小三角形；
第四步：对其余三个小三角形重复步骤一。


图5：谢尔宾斯基三角形（Sierpinski triangle）


4.著名学者简介

 

伯努·瓦曼德布洛特 Benoît B. Mandelbrot


图6：伯努·瓦曼德布洛特 Benoît B. Mandelbrot


法国、美国数学家（双国籍），最大的成就是创立了分形几何。1967年，曼德布洛特在美国《Science》杂志上发表题目为《英国的海岸线有多长》的划时代论文，标志着其分形思想的萌芽。

 

朱尔·亨利·庞加莱 Jules Henri Poincaré


图7：朱尔·亨利·庞加莱 Jules Henri Poincaré


法国最伟大的数学家之一，理论科学家和科学哲学家。庞加莱被公认是19世纪后和20世纪初的领袖数学家，是继高斯之后对于数学及其应用具有全面知识的最后数学家。早在19世纪初，庞加莱在研究三体问题中，使用了新的几何方法。

 

格奥尔格·康托尔Georg Cantor


图8：格奥尔格·康托尔Georg Cantor


德国数学家，创立了现代集合论，是实数系以至整个微积分理论体系的基础，构造了三分康托尔集。

 

海里格·冯·科赫 Helge von Koch


图9：海里格·冯·科赫 Helge von Koch


瑞典数学家，在他1904年的一篇论文“关于一个可由基本几何方法构造出的，无切线的连续曲线”（原文的法文标题为：“Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire”）中，他描述了科赫曲线的构造方法。

 

瓦茨瓦夫·谢尔宾斯基 Wacław Sierpiński


图10：瓦茨瓦夫·谢尔宾斯基 Wacław Sierpiński


波兰数学家，因对集合论、数论、函数的理论和拓扑学的出色贡献而闻名。两个著名的分形是根据他的名字命名：谢尔宾斯基三角形和谢尔宾斯基地毯；另外还有谢尔宾斯基数和谢尔宾斯基问题也是以他的名字命名。


费利克斯·豪斯多夫 Felix Hausdorff


图11：费利克斯·豪斯多夫 Felix Hausdorff


德国数学家，他是拓扑学的创始人之一，他定义和研究偏序集、豪斯多夫空间和豪斯多夫维，证明豪斯多夫极大定理（Hausdorff maximality theorem）。提出了豪斯多夫维数来计算分形维数。


5.相关资源推荐


书籍：


分形对象：形、机遇和维数 

Fractals:From,Chance,and Dimension

 

本书考察和研究出现在自然界中的若干典型分形对象，为我们提供了一个关于分形的内容，意义及方法的扼要介绍。尽管自该书第一版（法文版）问世以来，分形的理论及其应用发展极为迅速，并出现了大量的有关著作，但此书仍不失为分形理论最好的入门书之一。

分形对象：形、机遇和维数 

Fractals:From,Chance,and Dimension

http://rrd.me/gfyYz


大自然的分形几何 

The Fractal Geometry of Nature


这本书介绍了自然界中各种各样的分形理论，从海岸线、雪花，到河流、星系等自然现象，去阐述分形这一概念。作为多个学科的交叉，分形几何对以往欧氏几何不屑一顾（或说无能为力）的“病态”曲线（如科赫雪花曲线等）的全新解释，是人类认识客观世界不断开拓的必然结果。这说明欧氏几何只是对客观世界的近似反映，而分形几何则深化了这种认识，因此分形几何学是描述各种复杂自然曲线的大自然的几何学。

大自然的分形几何 The Fractal Geometry of Nature

http://rrd.me/gfzjk

 

市场的（错误）行为：风险、破产与收益的分形观点

The Misbehavior of Markets: A Fractal View of Financial Turbulence


《市场的（错误）行为》以分形视角观察金融市场的行为，推翻了作为当代金融分析基础的“随机游走”理论。通过分形模型，市场表现被重新阐释。本书是现代金融理论标准工具和模型的一次革命性重估，书中的观点颠覆了成千上万投资者的既有观念。

市场的（错误）行为：风险、破产与收益的分形观点The Misbehavior of Markets: A Fractal View of Financial Turbulence

http://rrd.me/gfz56


课程：


分形与奇异吸引子的几何学


此课程隶属于非线性动力学与混沌

本课程对非线性动力学和混沌进行了详细的讲解，强调分析方法、具体实例和几何直觉。主讲人为Steven Strogatz。


分形与奇异吸引子的几何学

https://campus.swarma.org/play/coursedetail?id=10621


分形的世界


在此堂课程，主要介绍了关于分形的思想与脉络，分形现象、分形维数、利用分形规律的计算方法以及混沌。主讲人为北京师范大学系统学院狄增如教授。狄增如教授主要从事复杂网络和经济（金融）物理学等方面的研究，是国内最早从事经济物理学研究的学者之一。


分形的世界

https://campus.swarma.org/play/coursedetail?id=10698


视频资源：

TED分享视频：Benoit Mandelbrot: Fractals and the Art of Roughness 伯努·瓦曼德布洛特: 分形和粗糙的艺术：

http://www.ted.com/talks/benoit_mandelbrot_fractals_the_art_of_roughness.html

纪录片：

Hunting the Hidden Dimension 寻找隐藏的维

https://www.bilibili.com/video/av13766486/?p=2

 电影:银河护卫队2、奇异博士等


资源网站：

分形艺术网：

http://www.fxysw.com/forum-12-1.html

关于分形的更多介绍：

http://webarchive.loc.gov/all/20011116035117/http://dmoz.org/science/math/chaos_and_fractals/


集智百科词条志愿者招募

 


以上的内容都只是非常简单的介绍，我们希望可以针对上面的每个知识点都进行扩充，使其变成一个可被大家广泛学习的科学词条。待建立的词条如下，共计12条：


知识概念：

 

分形几何

自相似

无标度特性

康托尔集（Cantor Set）

曼德布洛特集合（Mandelbrot set）

Julia集

谢尔宾斯基三角形（Sierpinski triangle）

 

书籍：


分形对象：形、机遇和维数 

Fractals:From,Chance,and Dimension


大自然的分形几何 

The Fractal Geometry of Nature

 

市场的（错误）行为：风险、破产与收益的分形观点

The Misbehavior of Markets: A Fractal View of Financial Turbulence

 

期刊：

 

Chaos，Soliton and Fractals




参考资料：


[1]分形，百度百科 :http://baike.baidu.com/view/83243.htm

[2]分形，维基百科:

http://zh.wikipedia.org/wiki/%E5%88%86%E5%BD%A2

[3]Mandelbrot set, WIKI :http://en.wikipedia.org/wiki/Mandelbrot_set

[4]Julia set, WIKI :http://en.wikipedia.org/wiki/Julia_set

[5]神奇的分形艺术（四）：

Julia 集和 Mandelbrot 集，Matrix67 http://www.matrix67.com/blog/archives/292

[6] 豪斯多夫维数

http://zh.wikipedia.org/wiki/%E8%B1%AA%E6%96%AF%E5%A4%9A%E5% A4%AB%E7%BB%B4%E6%95%B0

[7] 计盒位数 

http://zh.wikipedia.org/wiki/%E8%AE%A1%E7%9B%92%E7%BB%B4%E6%9 5%B0

[8] 科赫曲线，维基百科

http://zh.wikipedia.org/wiki/%E7%A7%91%E8%B5%AB%E6%9B%B2%E7%B 7%9A

[9]  谢尔宾斯基三角形

http://zh.wikipedia.org/wiki/%E8%AC%9D%E7%88%BE%E8%B3%93%E6%96%AF%E5%9F %BA%E4%B8%89%E8%A7%92%E5%BD%A2

[10]陈关荣老师关于分形的信息整理：

https://www.ee.cityu.edu.hk/~gchen/pdf/FractalsStories.pdf

[11]分形的代码演示：

http://www.fxysw.com/thread-4982-1-1.html

[12]IBM的分形：

https://www31.ibm.com/ibm/cn/ibm100/icons/fractal/impacts.shtml 

[13]浅谈分形几何学 http://www.yingzhenli.net/home/pdf/%E5%88%86%E5%BD%A2%E4%B8%8E%E6%B7%B7%E6%B2%8C.pdf 
[14]youtube上的视频：
https://www.youtube.com/watchv=PD2XgQOyCCk

参考资料可上下滑动查看



来源：集智百科
编辑：曾祥轩

推荐阅读


什么是元胞自动机？| 集智百科
谁是最“复杂”的小说：文学叙事中的长程关联与多重分形
如何用 Mathematica  窥探质数分布中隐藏的分形规律
系列公开课预告：掌握复杂性思维，应对瞬息万变的世界
加入集智，一起复杂！




集智俱乐部QQ群｜877391004

商务合作及投稿转载｜swarma@swarma.org

◆ ◆ ◆

搜索公众号：集智俱乐部


加入“没有围墙的研究所”

让苹果砸得更猛烈些吧！