
社会对个体某种行为的赞扬与否定这一行为称为社会强化效应,在信息传播中也起到了重要作用,这意味着信息传播的概率是会变化的。疾病传播也有类似效应。近期发表在Nature Physics上的一篇论文,提出了一个复杂传播模型,并建议针对网络上的信息疾病传播研究,应当优先使用复杂模型,而非SIR等简单模型。
如何对信息传播的过程建模?最初的选择是源于传染病的模型,例如经典的 SIR 模型,在此模型内将人群分为可感染,感染,已康复三种状态,再来拟合不同状态间的转移概率。
然而对于信息的传播,简单传染病模型忽略了现实中普遍存在的社会强化效应(social reinforcement),以及社会强化效应所带来复杂的局部模式。
例如一个人是否关注并传播肖战粉丝事件的讯息,周围朋友又有多少人已经在讨论这件事,如果关注的人太少,这则信息会被认为是小众爱好,而若是足够多人都在谈论这件事,即使不是粉丝,也想了解下事情的前因后果。
与之类似的是,病毒传播的概率,取决于所处环境中病毒的浓度,而浓度又取决于环境内患病人所占的比例。
针对社会强化现象,2月24日发表在 Nature Physics 的一篇题为论文给予了解答。
论文题目:
Macroscopic patterns of interacting contagions are indistinguishable from social reinforcement
论文地址:
https://www.nature.com/articles/s41567-020-0791-2
该文提出了一个针对疾病及模因传播都适用的复杂传播模型,所谓复杂传播模型,是对多种模型的统称,指考虑了传播过程中的参数变化及网络结构所带来非线性作用的模型。
研究者论证了相互作用的简单模型给出的结果和该文提出的复杂传播模型是等价的,因此,即使没有明确的证据指出传播机制是复杂的,也应该使用复杂传播模型来进行建模。
1. 为什么现实中传播的
过程不能只用SIR来建模
新冠肺炎让SIR模型为大众所知晓,然而在SIR这类模型中,假设了人群所携带具有传播性质的疾病只有一种。但在现实中,人群中会有多种疾病同时传播,社交媒体上也并存着数量众多的谣言。
例如,患流感之后再次感染新冠肺炎的几率,是会由于身体抵抗力下降而增加?还是会由于流感病毒占据了生态位而降低?这一类问题,目前还没有明确的研究,但不容忽视的是,同时传播的多种其他疾病,让某种疾病在人群中的传播过程变得没那么简单。
图1:人群中感染A疾病的邻居比例影响了B疾病的传播比例
在SIR模型中,疾病的传播率是固定的,平均传播率越大,感染人群也会单调地增加。然而在现实生活中,局部微小变化会引起整体显著改变。
例如一个人是否相信并传播某个信息,取决于他能看到多少次该信息。而是否相信一个信息,不同人是有不同阈值的。A只要看到群里有一个人对某条消息点赞,就会相信并接力点赞,而B看到已经有两个人点赞了,也认定这个消息为真并点赞,以次类推,最终群体内所有人都相信了这则谣言。但如果群体中任何一个人能够阻断传播,比如明确否定该消息,就能够避免谣言传递给所有人。
上述两个例子,分别论述了相互影响的传播过程及参数会发生变化的传播过程——由于真实情况下传播是动态且多元的,因此使用SIR模型来进行建模,模型的预测结果可能具有偏差。因此这项研究建议,将网络传播的默认模型调整为可证伪的复杂模型,如果发现复杂模型和实际情况无法吻合,再采取简单模型,诸如SIR模型进行预测。
基于最简单的SIS模型,复杂传播模型最大的创新在于引入β(I),β为代表传播率的函数,用来表示传播率会随着人群中感染人数(I) 的变化而改变。通过引入这个函数,可以解决上述的两个问题,即模拟多种传播源的情况,及在模型中引入可变的传播率,下面将细致地讲述这一过程。
在复杂模型中,人群感染密度的时序演化可用下式表示:
该模型引入了SS,SI,IS,II四种状态,分别代表没有感染A和B病毒的人、只感染A病毒的人、只感染B病毒的人、同时感染A和B两种病毒的人在人群中的密度。r1和r2分别代表A和B病毒的康复率,由此,在某一时刻,一个充分混匀的人群中,可以基于上一时刻情况II下写出如下方程,其他状态的演化方程也可以类似推出:
当模拟疾病在包含紧密连接的小团体(clique)与长程随机连接的网络上传播,我们需要分别考察感染人群的全局比例、局部内邻居感染比例、随机连接中有多少比例感染、相比远程连接局部连接的感染率比例这四个指标,如图 3 所示。
图3:SIS 框架下 三种传播模型(简单,复杂,相互影响)情况下传播过程中参数的对比
可以看出在总体的感染数目上,三种模型相近,但在除此之外的三个描述局部感染情况的指标上,简单模型有显著不同,而复杂模型和相互影响模型则表现相似,难以区分。这就用数据论证了简单的传染病模型,无法对包含社会强化效应的传播过程进行模拟。
由于在所有指标上,用复杂模型和相互影响模型,拟合效果都是相近的,因此相比之前的相互影响模型,复杂模型不会随着要考虑的病源数目的增加,引起模型中的参数指数级增加。而用简单模型进行建模,则符合奥卡姆剃刀原则。
在SIR模型中,变化曲线是光滑的,不存在突变点。但现实中却往往不是这样,病例会出现连续多天的零增长,之后忽然增加。微博中也会猛然出现一个热点,又忽然消失。这些涌现而出的现象说明了,使用SIR模型的预测会和真实显著偏离。复杂传播模型的第一个优点,就是能复现出临界点附近的非线性突变。
图4:相互影响的两种疾病如何促成感染率的非连续突变
上图中横轴是复杂模型下是病毒传播率和康复率的比率,纵轴是总的感染人群密度,不同的颜色代表了病毒B不同的参数。其中α代表两种同时传播的病毒之间相对传播率。
图中的红线代表存在两种病毒,且病毒之间相对传播率差异明显,从而一旦两种病毒的平均传播概率相比康复概率(1.5+0.5)/2大于1时,人群中就会有很大比例的人感染,而在此之前,感染的患者在没有传播之前就自愈了。
图中蓝线代表两种病毒相对率接近时,人群中感染的比例由感染概率较低的那种病毒决定,只有当另一种病毒感染的概率超过康复的概率后,人群中才可能出现感染者;而绿线代表两种传播率差异较大的病毒,此时即使两个病毒的平均康复概率小于1,随着感染几率接近康复几率,也会在人群中由于相变现象出现相当比例的人群感染。
网络中的局部结构,也会影响疾病的传播。例如局部存在节点之间同质性的社区,或者网络中心节点,由于内在属性的相似的发生聚集现象。在这种情况下,传播的过程和简单模型也有所不同。
然而这类的性质,也可以用复杂传播模型来模拟。这可以看成是存在两种不同的病毒,一种在社区内部传播时,传播率会增加,一种是在社区之间传播时,传播率会降低。如果传播的速率由于网络中存在聚集现象,那么局部邻居的之间状态的相关性会比仅仅根据网络结构推出的结果有所不同。
为了说明模型在真实场景下的应用,也为了说明不同于普通大众所认识的“传播率一成不变”,本文用两个真实场景中的例子,来根据真实数据反推传播率变化函数是怎样的,如下图所示。
左图是第一个例子,2009年社交媒体中,有多少相关的帖子是与著名Walter Cronkite之死相关的;右图是第二个例子,2005年波多黎各的登革热疫病的传播效率。每幅图中右上角分别表示随时间变化的事件发生次数,以及该事件的流行程度。
在社交媒体中,传播的信息越多,某条信息的模糊度就越小,从而人们传播这条信息的概率越低。而在疾病传播中,由于登革热存在多种亚型,康复的患者不容易再患上其他亚型的登革热,但仍然可以传播病毒。这导致了传播率的升高。之后由于易感人群大部分被感染再被治愈后,有了抗体,进而使得传播率下降。
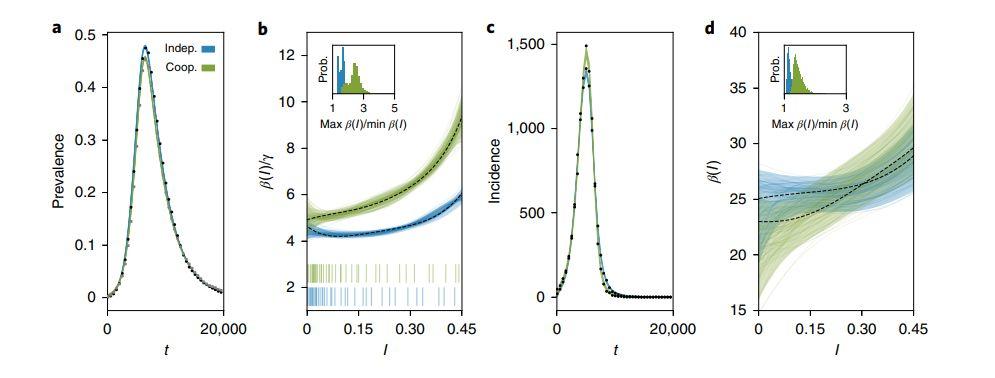 图6:传统SIR框架下,使用模拟数据,存在(绿色)不存在(蓝色)相互作用下推测传播率的变化
图6:传统SIR框架下,使用模拟数据,存在(绿色)不存在(蓝色)相互作用下推测传播率的变化
上图中,图a(流行程度)和图c(发生次数)中的两条线几乎没有区分,然而假设存在或不存在病源之间的相互作用,模型反推出的传播率变化函数显著区别。
由此通过复杂模型,在传播机制未知的情况下,模型能够通过推出传播率变化函数,再和实际数据对比,区分出是否存在多种病毒亚型,又或者病毒是否变异。
该模型还能够使用流行病学数据,揭示复杂的生物学机制,例如推出某种病源感染的几率是否和接触次数之间存在非线性的关系。
-
参数少,但能够模型多种相互影响的传播源
-
能够模拟非连续的变化
-
能建模网络中节点的聚集带来的影响
-
可证伪,能区分是否存在相互影响的传播源
因此,文中建议在无论考虑在生物学,传播学或是其他应用场景中,都优先使用引入了社交正反馈的复杂传播模型,即使没有证据表明存在非线性的作用或存在正反馈。
需要注意的是,该模型的局限在于其假设传播的信息/疾病是不可分,且人群是充分混杂的,每个人都可以传给周围的所有人,但真实情况会更复杂。
信息公开,分块隔离——基于信息扩散的新型肺炎网络传播模型
扩散信息、交通管制、自我隔离,哪个更能遏制病毒传播?
武汉新冠肺炎传播与控制简单的数学模型与预测
为什么病毒扩散这么快?从网络科学视角看大规模流行病传播
加入集智,一起复杂!

集智俱乐部QQ群|877391004
商务合作及投稿转载|swarma@swarma.org
搜索公众号:集智俱乐部
加入“没有围墙的研究所”
让苹果砸得更猛烈些吧!
👇点击“阅读原文”,了解更多论文信息


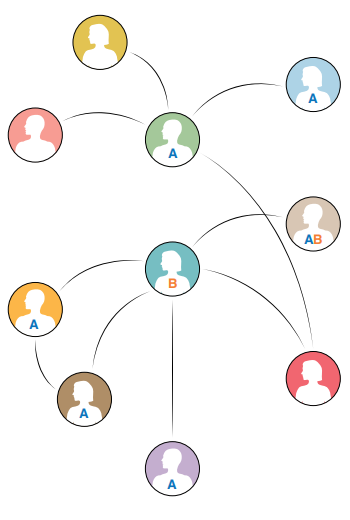

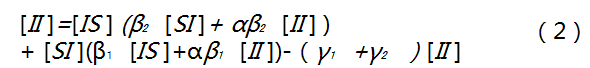

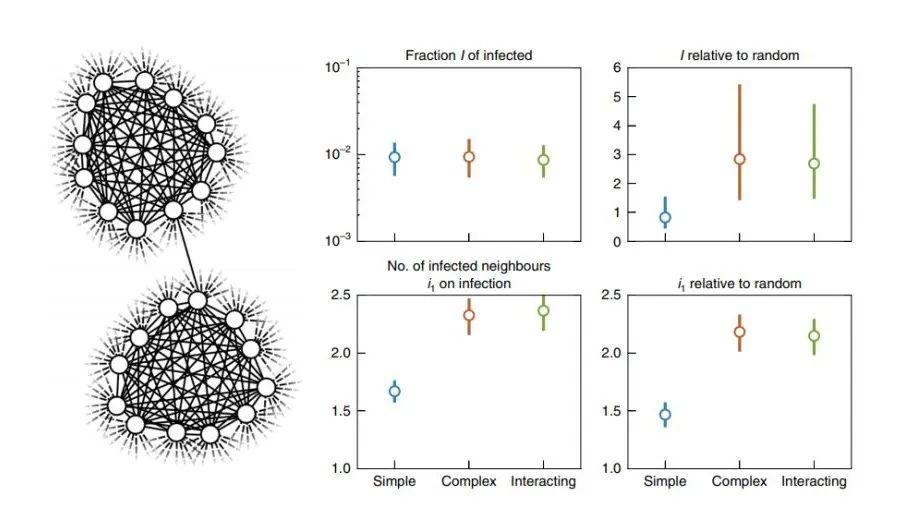

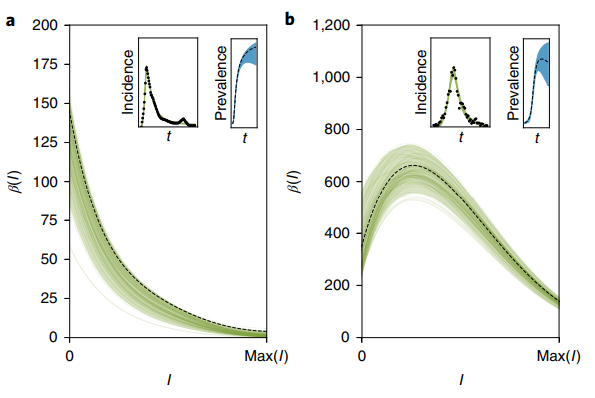
 图6:传统SIR框架下,使用模拟数据,存在(绿色)不存在(蓝色)相互作用下推测传播率的变化
图6:传统SIR框架下,使用模拟数据,存在(绿色)不存在(蓝色)相互作用下推测传播率的变化











