什么是康威生命游戏 | 集智百科

目录
一、什么是生命游戏?
二、生命游戏的规则
三、生命游戏的模式示例
四、生命游戏的应用
五、相关人物
六、相关资源推荐
七、集智百科词条志愿者招募
康威生命游戏(Conway’s Game of Life),又称康威生命棋,是最著名的二维元胞自动机,由英国数学家约翰·康威(John H. Conway)发明,1970年10月,通过马丁·加德纳(Martin Gardner)在《科学美国人》开设的专栏中得到普及。游戏像“病毒”一样在世界范围内传播。
尽管这个游戏中的规则是完全确定的,但是很难预测几个步骤后的状态。简单来说,该游戏是零玩家游戏,这意味着我们只能设定其初始状态,并观察其演变,它的发展由其初始状态决定。
它是具有图灵完整性的,可以模拟通用构造器或任何其他图灵机。也就是从理论上来说单元格空间足够大、数量足够多、计算能力足够强,生命游戏甚至可以模拟出与和真实生命程度相当的复杂性。
图1:生命游戏具有图灵完整性
二、生命游戏的规则
二、生命游戏的规则
我们所说的生命游戏是一个无限的,由二维正交正方形的网格组成的计算机模拟图像。每个单元可能出现两种状态:活或死的(填充或未填充的分别)。每个单元格都与其八个相邻的单元交互,这八个单元格是水平、垂直或对角线相邻的单元格。在每个时间步上,都会发生以下变化:
-
当前元胞为存活状态时,如果周围的存活元胞数小于2或大于3,该元胞变成死亡状态。
-
当前元胞为存活状态时,如果周围有2个或3个存活元胞时,该元胞保持原样。
-
当前元胞为死亡状态时,如果周围有3个存活元胞时,该元胞变成存活状态。
可以把最初的元胞结构定义为种子,当所有在种子中的元胞同时被以上规则处理后,可以得到第一代元胞图。按规则继续处理当前的元胞图,可以得到下一代的元胞图,周而复始。

图2:生命游戏示例
三、生命游戏的模式示例
1.生命游戏的Netlogo代码实现
patches-own[living]to setupclear-allreset-ticksask patches[if random-float 1 < 0.5 [set pcolor white]set living 0]endto goask patches[set living count neighbors with [pcolor = black]]ask patches[ifelse pcolor = black[if living > 3 or living < 2[set pcolor white]][if living = 3[set pcolor black]]]tickend
注代码解释:代码整体分为两部分,setup和go部分。其中setup进行环境的初始化,go进行持续运行。
2.生命游戏的模式示例
在生命游戏中会出现许多不同类型的模式,这些模式根据其行为进行分类。常见的模式类型包括:
-
静态:从一代到下一代都不会改变;
-
振荡态:经过有限的迭代后返回其初始状态;
-
移动的震荡态:它们可以在整个网格中平移。
静态示例


方块 船
震荡态示例


脉冲星(周期=3轮) 烽火(周期=2轮)
移动态示例


滑翔机(周期=4轮) 太空船(周期=4轮)
自从发明以来,康威的《生命游戏》就吸引了人们的极大兴趣,这是因为自动机的状态发展令人惊讶。生命游戏是产生并自我组织的一个例子。计算机科学,物理学,生物学,生物化学,经济学,数学,哲学和生成科学等各个领域的学者都可以用这种通过执行简单规则即可产生复杂模式的方式。
生命游戏也可以用作教学分析,用于展现有些反直觉的观念,即设计和组织可以在没有设计师的情况下自发出现。例如,认知科学家丹尼尔·丹内特(Daniel Dennett)广泛使用了康威生命游戏中的 “宇宙” 的类比,来说明复杂的哲学构造(如意识和自由意志)可能从相对简单的确定性物理定律集演化而来,而这些定律可以控制我们的宇宙。

图3:约翰·康威 John H. Conway
约翰·康威 John H. Conway:英国数学家、生命游戏发明者。1964 年在剑桥大学获得博士学位,并留校任教。1984 年来到普林斯顿大学数学系任教。他对群体理论,分析,拓扑,数论,几何,代数和组合博弈论做出了重要的贡献。生命游戏大大拓宽了元胞自动机的研究,并吸引很多人进入了复杂性科学和人工生命的研究中。
其深刻而通达的作品,超乎寻常的个性,古怪的幽默感以及与任何人谈论数学并使之倾听的能力,使他成为了他所到之处的,数学家与业余爱好者的关注焦点及流行偶像一样的人物。
他生前热爱各种游戏,有几项最重要的成就是在他思考游戏及其策略的时候达成的。康威最大的发现曾震惊数学界,他找到了数字与游戏之间令人惊讶的对应关系,这使他建立了一个真正的巨大系统—超现实的数字。它不仅包含我们都知道的正负实数,还包含无限大的新数字,无限小的新数字以及介于两者之间的各种新数字。
康威因与COVID-19相关的并发症去世,享年82岁。此次疫情虽然夺去了生命游戏之父的生命,但是生命游戏将永远继续下去,我们将永远缅怀他。
相关阅读:
六、相关资源推荐
六、相关资源推荐
书籍
《On Numbers and Games》

图4:On Numbers and Games
《On Numbers and Games》这本书是为数不多的不仅极具创造活力,同时又在几十年中依旧保持着其影响力的书籍。最初是为了定义超数数理论与数学游戏之间的关系而写的,最终成为了一本数学上精巧且极为有趣的博弈论指南。对于稍有数学背景的读者,这本书一步一步的引出新定义的数字系统,让我们了解专业的数学家是如何从一些简单易懂的内容入手,来获得具有普遍性且专业的知识。

NetLogo多主体建模入门 https://campus.swarma.org/course/1095/?from=official
网站
conwaylife
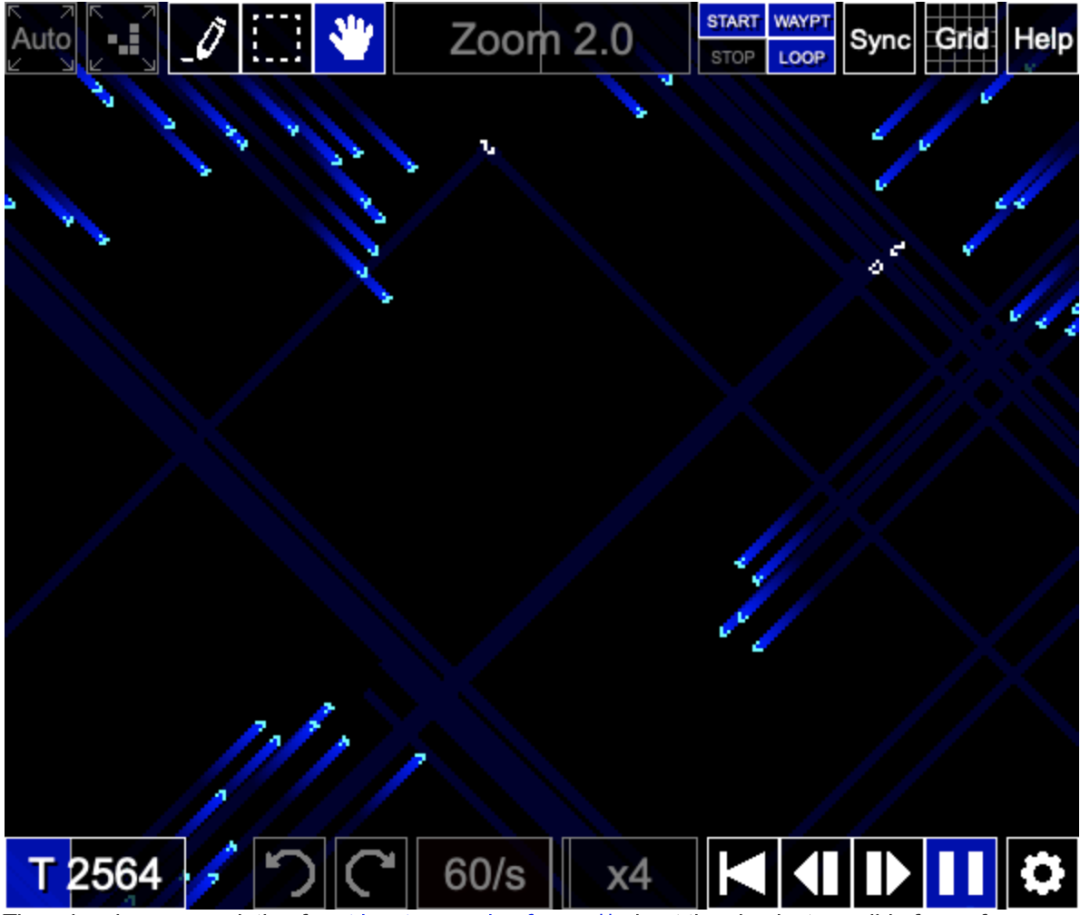
图5:conwaylife示例
conwaylife:
https://conwaylife.com
七、百科项目志愿者招募
七、百科项目志愿者招募
作为集智百科项目团队的成员,本中文词条由11795、Ilseyao1980、张朔、李媛翯编辑,欢迎在讨论页面留言。。我们也为每位作者和志愿者准备了专属简介和个人集智百科主页,更多信息可以访问其集智百科个人主页:



在这里从复杂性知识出发与伙伴同行,同时我们希望有更多志愿者加入这个团队,使百科词条内容得到扩充,并为每位志愿者提供相应奖励与资源,建立个人主页与贡献记录,使其能够继续探索复杂世界。
欢迎扫描下方二维码添加负责人加入集智百科团队!
参考资料:
[1].https://mathworld.wolfram.com/GameofLife.html
[2].http://wiki.swarma.net/index.php/生命游戏集智百科
[3].https://www.nature.com/articles/d41586-020-01515-1
[4].https://conwaylife.com
来源:集智百科 编辑:曾祥轩
推荐阅读

集智俱乐部QQ群|877391004
商务合作及投稿转载|swarma@swarma.org
◆ ◆ ◆
搜索公众号:集智俱乐部
加入“没有围墙的研究所”

让苹果砸得更猛烈些吧!
👇复杂世界,生命游弋,简单规则探寻生命的“本质”,点击“阅读原文”,创造你的世界。










