什么是李雅普诺夫函数 | 集智百科

本文是对集智百科中“李雅普诺夫函数”词条的摘录,参考资料及相关词条请参阅百科词条原文。
本词条由集智俱乐部众包生产,难免存在纰漏和问题,欢迎大家留言反馈或者前往对应的百科词条页面进行修改,一经修改,可以获得对应的积分奖励噢!
目录
一、什么是李雅普诺夫函数?
二、李雅普诺夫函数的定义
三、相关术语
四、自治系统的基本李雅普诺夫定理
五、例子
六、相关资源推荐
七、集智百科词条志愿者招募
1. 什么是李雅普诺夫函数?
在常微分方程理论中,李雅普诺夫函数 Lyapunov functions 是可用来证明常微分方程平衡点 equilibrium point稳定性的标量函数 scalar function 。李雅普诺夫函数是以俄罗斯数学家亚历山大·李雅普诺夫 Aleksandr Lyapunov 的名字命名,也称为稳定性的李雅普诺夫第二方法。对于动力系统 dynamical system 的稳定性理论 stability theory 和控制论 control theory 十分重要。在一般状态空间马尔可夫链 Markov chains 理论中也出现了类似的概念,通常称为Foster-Lyapunov 函数。
对于某些类型的常微分方程,李雅普诺夫函数的存在性是其稳定性的充要条件。尽管对于常微分方程没有构造李雅普诺夫函数的一般方法,但在许多特定情况下,李雅普诺夫函数的构造是已知的。例如,二次函数满足一个状态的系统的李雅普诺夫函数;一个特定线性矩阵不等式的解为线性系统提供了李雅普诺夫函数;守恒律 Conservation law 通常可以用来构造物理系统的李雅普诺夫函数。
2. 李雅普诺夫函数的定义
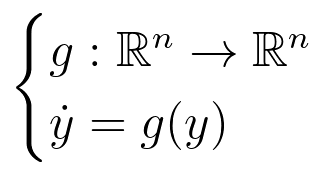
 ,该函数连续、具有连续的一阶导数且局部正定,
,该函数连续、具有连续的一阶导数且局部正定,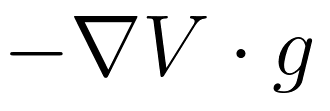 也是局部正定的。有时把
也是局部正定的。有时把 局部正定的条件表述为
局部正定的条件表述为 是局部负定的。
是局部负定的。3. 相关术语
对李雅普诺夫函数出现在动力系统平衡点的研究中。在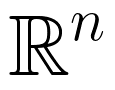 空间中,任意一个自治动力系统都可以被写成:
空间中,任意一个自治动力系统都可以被写成:
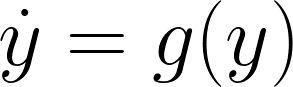

 的点y∗。给定一个平衡点y∗,总是存在一个坐标变换x=y−y∗,使得:
的点y∗。给定一个平衡点y∗,总是存在一个坐标变换x=y−y∗,使得:
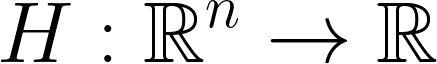 ,函数沿动力学系统解取值的时间导数为:
,函数沿动力学系统解取值的时间导数为:
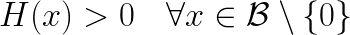
4. 自治系统的基本李雅普诺夫定理
令 是如下自治系统的平衡点
是如下自治系统的平衡点

并使用 表示李雅普诺夫候选函数 Lyapunov-candidate-function V的时间导数:
表示李雅普诺夫候选函数 Lyapunov-candidate-function V的时间导数:

局部渐进稳定平衡点 Locally asymptotically stable equilibrium
如果平衡点是孤立的,李雅普诺夫候选函数V是局部正定的,其时间导数是局部负定的:

对于原点的某些邻域 ,可以证明平衡点是局部渐近稳定的。
,可以证明平衡点是局部渐近稳定的。
稳定平衡点 Stable equilibrium
如果V是李雅普诺夫函数,那么平衡点是李雅普诺夫稳定的。
反之亦然,J. L. Massera证明了这一点。
全局渐进稳定平衡点 Globally asymptotically stable equilibrium
如果李雅普诺夫候选函数V是全局正定、径向无界的,平衡点是孤立的,且李雅普诺夫候选函数的时间导数是全局负定的:
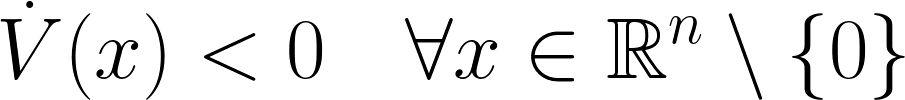
可以证明平衡点是全局渐近稳定的。
如果满足:

李雅普诺夫候选函数 是径向无界的。(这也被称为范数强制。)
是径向无界的。(这也被称为范数强制。)
5. 例子
在统计学和经济学中,因果关系通常通过回归分析来检验。
考虑下面具有 上的解x的微分方程:
上的解x的微分方程:

考虑到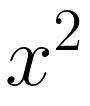 在原点附近始终为正,因此自然而然地成为帮助我们研究x的李雅普诺夫候选函数。
在原点附近始终为正,因此自然而然地成为帮助我们研究x的李雅普诺夫候选函数。
令 在
在 上。然后有
上。然后有

这正表明上面的微分方程 x关于原点是渐近稳定的。注意,使用相同的李雅普诺夫候选函数可以证明该平衡点也是全局渐近稳定的。
6. 相关资源推荐
本课程主要讲授连续和离散动力系统的定态、极限环及其稳定性分析、动力学系统的结构稳定性和常见的分支类型以及分析方法,混沌概念等。

课程名称:动力系统分析
课程地址:https://campus.swarma.org/course/1641
7.百科项目志愿者招募
作为集智百科项目团队的成员,本文内容由Jxzhou、Ruili、薄荷参与贡献。我们也为每位作者和志愿者准备了专属简介和个人集智百科主页,更多信息可以访问其集智百科个人主页。



点击图片看一看这一周我们做了啥
在这里从复杂性知识出发与伙伴同行,同时我们希望有更多志愿者加入这个团队,使百科词条内容得到扩充,并为每位志愿者提供相应奖励与资源,建立个人主页与贡献记录,使其能够继续探索复杂世界。
如果你有意参与更加系统精细的分工,扫描二维码填写报名表,我们期待你的加入!

来源:集智百科 编辑:曾祥轩
点击“阅读原文”,阅读李雅普诺夫函数相关内容与文献











