PC算法：缺失数据下的因果发现

导语

在各种跟数据打交道的科学研究中，都需要通过观测变量或对变量进行干预试验，从而发现其中的因果关系。但在许多实际研究中，会面临数据不全或数据缺失。在集智俱乐部因果读书会第三期中，来自瑞典皇家工学院的屠睿博，讲述了数据缺失会怎样影响因果发现，并介绍了怎样使用基于贝叶斯网络的PC算法框架来应对数据丢失。本文是对分享的文字整理。

对因果发现不熟悉的读者，可以查看我们根据卡耐基梅隆大学博士生黄碧薇的分享所整理的文章：因果发现：如何让算法成为复杂系统中的“福尔摩斯”？

郭瑞东 | 讲者

屠睿博 | 整理

邓一雪 | 编辑

1. 数据缺失带来错误的因果关系

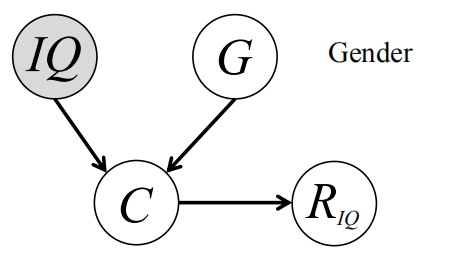
举一个假设的例子，来说明数据缺失可能带来的问题。假设大学的录取，取决于智商高低，同时比较倾向于录取男性，且智商测试只在大学中进行。在这样的场景下，如果在统计数据中，删除包含缺失项的第二和第三行，那么就智商和性别的关系这一问题，就会得出“如果是女性，则平均智商更高”这样一个错误的因果关系。

图1. 虚拟场景下，标红的数据缺失，导致错误结论

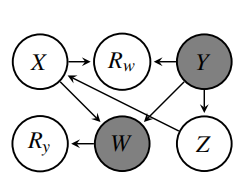
用因果图来描述上述场景，以及包含缺失值的变量智商，可以得出下图：

图2. 智商和性别共同影响大学录取，而使用大学录取后的数据，由于IQ项的缺失，造成有误导性的因果关系被发现

为了解决数据缺失给因果发现带来的问题，首先要考虑的问题是，如何用因果图表示数据丢失机制。

图3

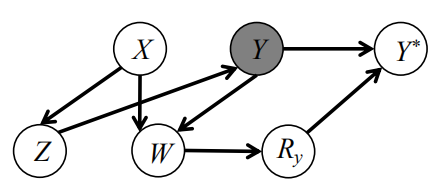
例如上图的代码中，Ry是数据缺失指示变量 (missingness indicator)，它代表了变量Y的数据中是否包含丢失数据。同时，因为Ry的数值由变量W决定，所以变量W被称为是缺失指示变量Ry的直接原因（direct cause）。

该数据丢失机制可以通过以下的因果图（missingness graph）[1]表示。图中的代理变量Y*（proxy variable）表示观测到的含有丢失数据的Y变量。由于Y，Ry和Y*的关系可以唯一确定，所以后文因果图中将不画出Y*。

图4. 包含数据缺失机制的因果图示例

上文的例子是基于假定丢失机制的模拟环境，在真实场景中，需要根据常识和领域知识，对数据缺失的机制进行假设。

2. 三种不同的数据缺失类型

所有可能数据缺失，可以按照丢失机制，分为三类，这三类涵盖了所有可能的数据缺失[4]。

第一类是完全随机的数据缺失（Missing Completely At Random），即数据是否缺失，和所有观测的变量完全无关。例如由于硬盘故障，网络丢包等与待研究问题完全无关的随机性造成的，简称MCAR。

图5. MCAR对应的因果图

第二类称为受随机因素影响的数据缺失（Missing At Random），即数据是否缺失的概率，是和某个可观测变量的值有关的。例如某些组的受试者更有可能不愿意配合实验者，导致这一组额度数据中，缺失的比例更大，简称MAR。

图6. MAR对应的因果图

第三类称为数据缺失不随机（Missing Not At Random），即数据缺失时，不清楚缺失的数据属于哪个组。例如网购中，如果对商品的评分的人，要么是很喜欢这件商品，要么是很讨厌这件商品的。这意味着购买者是否给商品打分，取决于购物者对商品的评价。在这种最复杂的情况下，应对缺失问题更为困难。

图7. MNAR对应的因果图

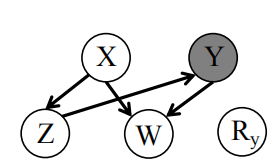
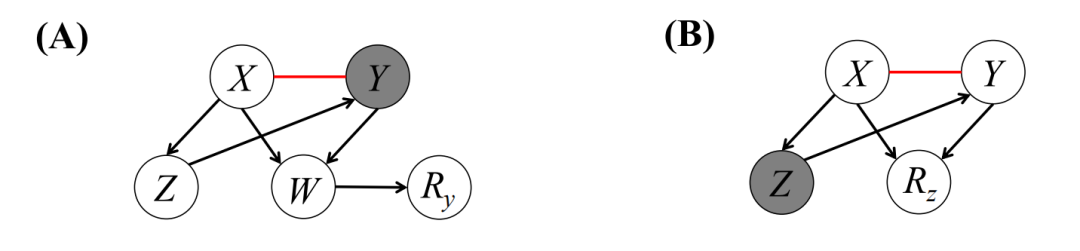
有了因果图，在满足一些比较弱的条件下，可以证明出数据缺失，只会在包含对撞因子的场景下，造成下图所示的两种可能的错误因果关系被发现。

图8. 可能的由数据缺失带来的错误连边示意图

这意味着想要解决缺失数据下的因果关系，只需要针对这两种情况下，判断图中的红边是否是误导性的。

3. 哪些数据缺失对因果发现是可解决的

不是所有因果发现中的数据缺失问题，都是可以解决的，必须在满足以下四个假设时，问题才是可解：

首先，缺失指示变量不能作为观测变量或者其他缺失指示变量的原因，也就是没有任何一个非代理变量的数值取决于数据是否缺失。

第二个假设，称为可信的观察。即在包含数据缺失和不包含缺失数据的两个“平行宇宙”中，待发现的因果关系及变量间的统计独立性不变。即不会由于观察包含缺失，导因果关系的改变。这可以看成之前可靠性假设（Faithfulness）的延伸。

第三，数据是否缺失之间，是相互独立的，不会出现变量X丢失，一定导致变量Y丢失最后一点是不包含自我抹去数据。即变量X是否丢失，如果是由于x本身的值决定的，这种情况下也是从理论上无法解决的。

第四，无自我缺失机制。观测变量本身不可是其数据缺失的愿意，比如一个自我缺失的例子可能是身高高于190cm或低于140cm的人群可能不愿意在填写表格时输入真实身高数据。

4. 包含缺失数据的PC算法

不论基于打分，还是基于模型的算法，都可以通过改进算法，来应对缺失数据。本文针对PC算法，详细解说如何修正算法。

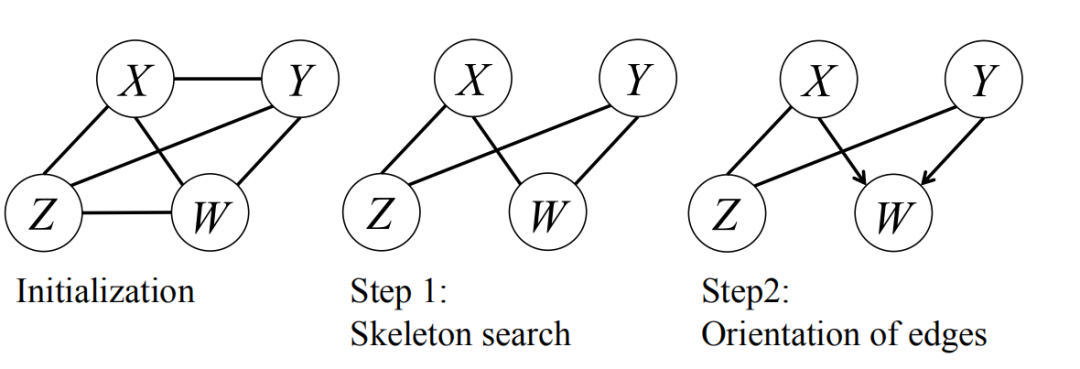
PC算法[2]首先初始化生成变量之间的全连接图，之后第一步是搜索因果图的骨架，第二步是确定因果方向，如下图所示：

图9. PC算法

为了应对缺失数据，主要的修改在第二步：首先在骨架搜索后，要对所有缺失的数据项，通过统计独立性，检测出是由哪些变量导致的，之后找出所有可能的错误的因果关系（边），再更正可能的错误的边。

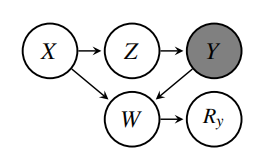
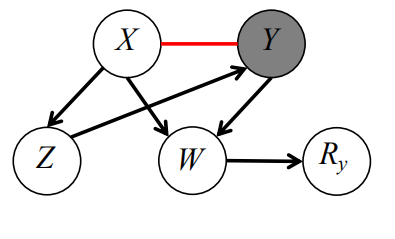
图10. 前文代码对应的因果图，其中X与Y之间可能存在错误的因果联系

上图的例子中，已经找到了X和Y之间可能存在错误的因果联系。但由于数据缺失与否，取决于对撞因子W，因此在去除不完整数据只考虑完整数据的情况下，无法通过统计独立性，判定X和Y之间不存在因果关系。这就是传统的PC算法为何无法解决数据缺失的原因。

图10. 新方法[3]通过构建数据补全器，解决数据缺失

在理想世界中，不存在数据缺失。如果能通过统计方法，基于缺失后的数据，估计出理想世界的情况，那么就能够在理想世界中进行因果发现，并解决数据缺失带来的问题。这类似于机器学习中的半监督学习，也是因果推断中常见的解决问题套路。

在假定线性高斯模型时可以通过三个包含权重和噪声项的线性方程，来描述W和XYZ之间的关系，并通过线性回归和观测数据，学到由W到XYZ的数据补全器，从而使生成的数据满足理想世界的数据分布。

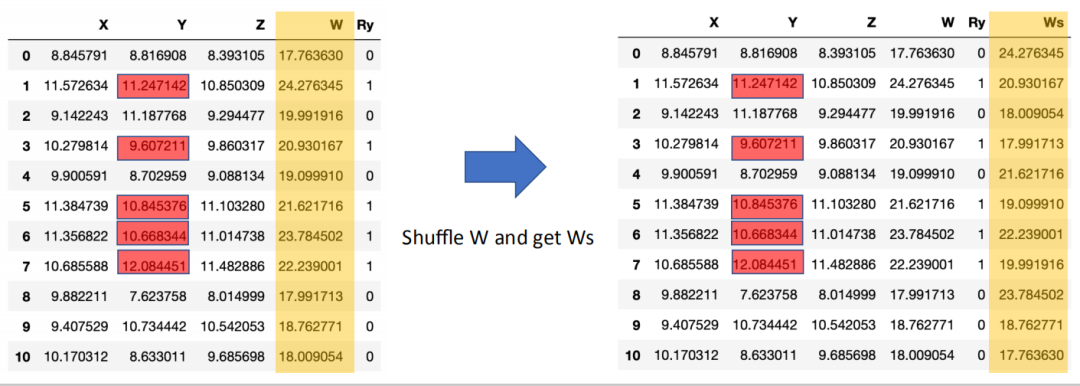
为了消除W和Ry是否缺失之间存在的关联，通过将数据中的W打乱，同时保留代表是否缺失Ry的值不变，如下图所示：

图11

最后在打乱后的Ws中，根据学到的数据补全器和线性回归模型的残差，还原出理想世界的X’，Y’和Z’。保持原有的样本数不变，通过在X’，Y’和Z’中进行统计检测，最终纠正错误的因果联系。

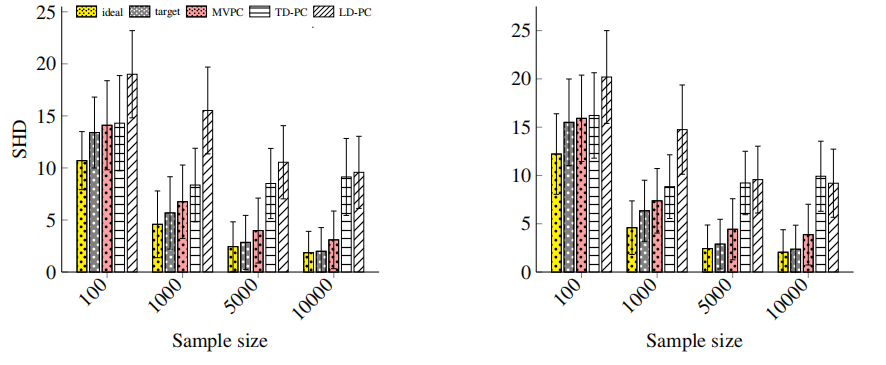
在生成的模拟数据中，MVPC的算法的表现，不论对于MAR或者MNAR，随着样本量的增加，其表现接近理想和目标情景。

图12. 模拟数据下MVPC算法的效果

机器学习中，经常包含数据缺失，即无标签的数据。如果想将因果发现应用在机器学习中，那就需要考虑在更少假设下的情况。对此可以参考碧薇的讲座，其中的讨论更加系统化。

参考文献

1. Mohan, Karthika, Judea Pearl, and Jin Tian. “Graphical models for inference with missing data.” Advances in neural information processing systems. 2013

2. Rubin, Donald B. “Inference and missing data.” Biometrika 63, no. 3 (1976): 581-592.

3. Spirtes, P., Glymour, C., Scheines, R., Kauffman, S., Aimale, V., & Wimberly, F. (2000). Constructing Bayesian network models of gene expression networks from microarray data

4. Ruibo Tu, Cheng Zhang, Paul Ackermann, Karthika Mohan, Clark Glymour, Hedvig Kjellström, and Kun Zhang. Causal discovery in the presence of missing data. In International Conference on Artificial Intelligence and Statistics (AISTATS), 2019.

推荐课程

本文整理自瑞典皇家工学院在读博士屠睿博在“因果科学与Causal AI”读书会上的分享，更多详细内容请参考录播视频，内附PPT。