什么是图（抽象数据类型）| 集智百科

“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

本文是对集智百科中“图（抽象数据类型）”词条的摘录，参考资料及相关词条请参阅百科词条原文。

本词条由集智俱乐部众包生产，难免存在纰漏和问题，欢迎大家留言反馈或者前往对应的百科词条页面进行修改，一经修改，可以获得对应的积分奖励噢！

一、什么图（抽象数据类型）

二、操作方式

三、表示方法

四、图的并行化表示

五、集智百科词条志愿者招募

图（抽象数据类型）：

https://wiki.swarma.org/index.php?title=图（抽象数据类型）

1. 什么是图（抽象数据类型）

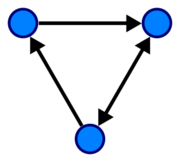
在计算机科学中，图是一种抽象的数据类型，它实现了数学中图论领域的两个概念：无向图 undirected graph和有向图 directed graph。

一个图的数据结构由一组有限的（也可能是可变的）顶点 vertices（也称为节点 nodes或点 points），以及一组边edges （也称为链接 links或直线 lines）构成。这里，每条边都是由顶点集合中的两个彼此不同的顶点构成；换句话说，每条边都是由图中的一对顶点构成的。根据构成每条边的顶点对是有序对还是无序对，图可以分成有向图 directed graph 和无向图 undirected graph；对于无向图而言，构成其每条边的顶点对是无序的，而有向图中，构成每条边的顶点对是有序的，这样我们也称有向图中的边为箭头arrows。在图数据结构中，顶点可以是以下三种类型的数据：1. 图结构的一部分；2. 由整型数索引表示的外部实体对象；3. 由引用references表示的外部实体对象。

一个有三个顶点（蓝色圆圈）和三条边（黑色箭头）的有向图。

图的数据结构还可以为每条边关联某个边值 edge value，如符号标签或数值属性（成本、容量、长度等）。

2. 操作方式

图形 G 的数据结构提供的基本操作通常包括：

adjacent (G, x, y)：检验顶点 x 到顶点 y 是否存在边；

neighbors (G, x)：列出所有满足这样条件的顶点y：给定的顶点x有一条边连到了顶点y;

add_vertex (G, x)：添加新顶点 x ；

remove_vertex (G, x)：删除已有顶点 x ；

add_edge (G, x, y)：添加一条连接顶点 x 和顶点 y 的边；

remove_edge (G, x, y)：删除连接顶点 x 和顶点 y 的边；

get_vertex_value (G, x)：返回与顶点 x 关联值；

set_vertex_value (G, x, v)：将顶点 x 的关联值设置为 v 。

将值关联到边的结构通常还提供：

get_edge_value (G, x, y): returns the value associated with the edge (x, y);

set_edge_value (G, x, y, v): sets the value associated with the edge (x, y) to v.

3.表示方法

实际应用中，用以表示图的各类数据结构：

邻接表 Adjacency list

顶点被存储为记录或对象，并且每个顶点存储一个相邻顶点列表。这种数据结构允许在顶点上存储额外的数据。当边也被存储为对象时，这些对象就可以作为额外的数据存储在顶点上；这个时候在每个顶点的数据结构中，存储了所有和这个顶点相邻的边，并且其中每条边存储了它所连接的两个顶点。

邻接矩阵 Adjacency matrix

一个二维矩阵，其中行表示源点 source vertices，列表示终点 destination Vertices。边和顶点上的数据必须存储在外部。这个矩阵只能存储每条边的权重值，这个值所在的行表示这条边的源点，它所在的列表示这条边的终点。

关联矩阵 Incidence matrix

一个二维布尔矩阵，其中行表示顶点，列表示边。矩阵中每个元素entry（也常译作“条目”）的值（要么是0，要么是1）表明这个元素所在的行上的顶点是否与它所在的列上的边是相关联。

下表给出了对上面所述的三种数据结构（对抽象的图的表示）进行各种操作的时间复杂度 time complexity。表中符号| V |表示顶点的数量，符号| E |表示边的数量。在邻接矩阵表示中，矩阵中的每个元素（条目）值是对这个元素所表示的边的权重的编码。若这个元素所表示的边在这个矩阵所表示的图中不存在，那么设这个元素的值为∞。

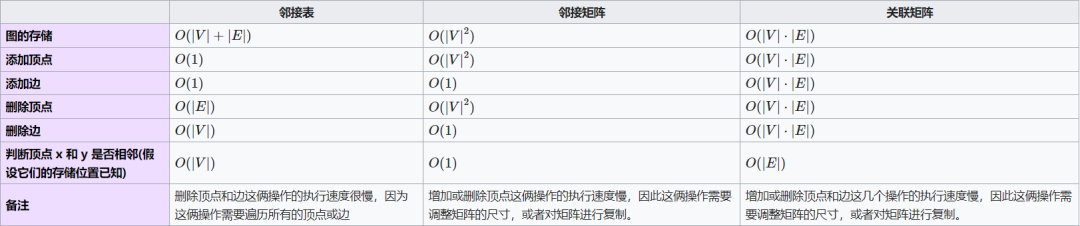
邻接表通常是首选的，因为它们能有效地表示稀疏图 Sparse Graph。如果图是稠密的 dense，即边的数目| E |接近于顶点数目的平方，| V |²，那么邻接矩阵是首选的。如果我们必须能快速查证，图上是否存在一条边连接了两个顶点，那么邻接矩阵也是首选的。

4. 图的并行化表示

图问题的并行化面临着这几个重大挑战：数据驱动的计算、无结构问题、糟糕的局部性以及数据访问占计算量比例高。在面对这些挑战时，用于并行架构的图表示（某种表示抽象的图的数据结构）扮演了重要的角色。糟糕的图表示有可能给算法增加不必要的通信成本，从而降低了算法相对于数据规模的扩展性。接下来的段落中，我们将着重探讨共享式和分布式的存储器架构。

共享式存储器

用于并行计算的图表示与顺序计算的图表示是一样的。这是因为在共享内存模型中，并行地对图表示（例如一个邻接表）进行只读访问是高效的。

分布式存储器

在分布式存储模型中，常用的方法是将图的顶点集合分解为个不相交的子集。这里，是可用的计算单元 processing elements（PE）的数量。随后，这这些顶点集的子集和每个子集相应的边各自构成子图，被分配给各个索引匹配的PE。每个PE都有自己的子图表示（某种表示抽象的图的数据结构），这里需要特别注意有端点在其他PE中的边。对于具有像 MPI 这样的标准通信接口的PE，一旦其中的子图有边连接到其他PE中的子图，那么这些PE的ID必须是可识别的。在分布式图算法的计算过程中，沿着这些边传递信息意味着PE之间进行了通信。

要小心仔细地对图做分割 —— 分割的时候要注意，在（计算单元间的）通信量的高低和（每个计算单元所均匀分得的子图的）尺寸大小之间有一个权衡。然而实际计算出最优分割是不可能的，因为图的分割是一个NP-hard问题。因而，我们退而求其次，用下列启发式方法。

1维分割：每个PE都会获得个顶点以及这些顶点的全部连出边 outgoing edges。对于那些要对各个PE上的子图表示执行操作的算法，这里需要一个步骤来进行PE之间的全互换通信 all-to-all communication，以及用于这种通信的报文缓冲区。考虑到每个PE中的顶点都可能有一些连出边，这些边各自连接了每一个其他PE中的某些顶点，因此，全互换通信是所有PE之间的，并且每个PE的报文缓冲区尺寸为，这里是图中边的数量。

2维分割：每个PE都获得一个邻接矩阵的子矩阵。假设全部个PE排成一个矩形阵列，阵列有行列，这样阵列总尺寸为。那么，用这个矩形阵列来分割邻接矩阵，每个PE都获得一个维的子邻接矩阵。这种对邻接矩阵的分割形如棋盘格。这样一来，根据邻接矩阵的定义，每个PE所分得的顶点最多只能连接到和这个PE同行或同列其他PE中的顶点，而不可能连接到在此之外PE的顶点。这就把每个PE在全互换通信中，有可能需要交换报文的PE数量从个限制为个。