网络重构最新综述推荐：从宏观尺度到微观尺度

导语

如何利用部分网络数据推断网络的宏观属性？能否进一步推断出网络中隐藏的链接模式，乃至补全中的具体节点与连边？最近arXiv的一篇综述文章，以统计物理和信息理论的视角，从宏观、介观和微观三个尺度讨论了解决网络重构问题的思路、方法和技术，本文是对综述整体内容的介绍。综述原文106页，扫描下方二维码即可查看下载PDF文件。

扫码获取论文PDF

陈昊 | 作者

刘培源 | 审校

邓一雪 | 编辑

数据缺失是数据分析过程中遇到的普遍问题。即使在大数据时代，由于注释错误、难以采集和隐私保护等问题，数据仍可能是不完整的。而在非结构化的网络数据中，该问题显得更加突出。在研究社会、经济和生物等系统时，解决网络结构的数据稀缺性的需求导致了网络重构这一研究领域的诞生。

最近一篇挂上arXiv上的网络重构领域综述文章《Reconstructing networks》将网络重构领域的研究划分为宏观、介观和微观三部分，对不同尺度的网络重构问题及研究进展进行了详尽的介绍。

论文题目：

Reconstructing networks

论文地址：

https://arxiv.org/abs/2012.02677

1. 宏观尺度的网络重构

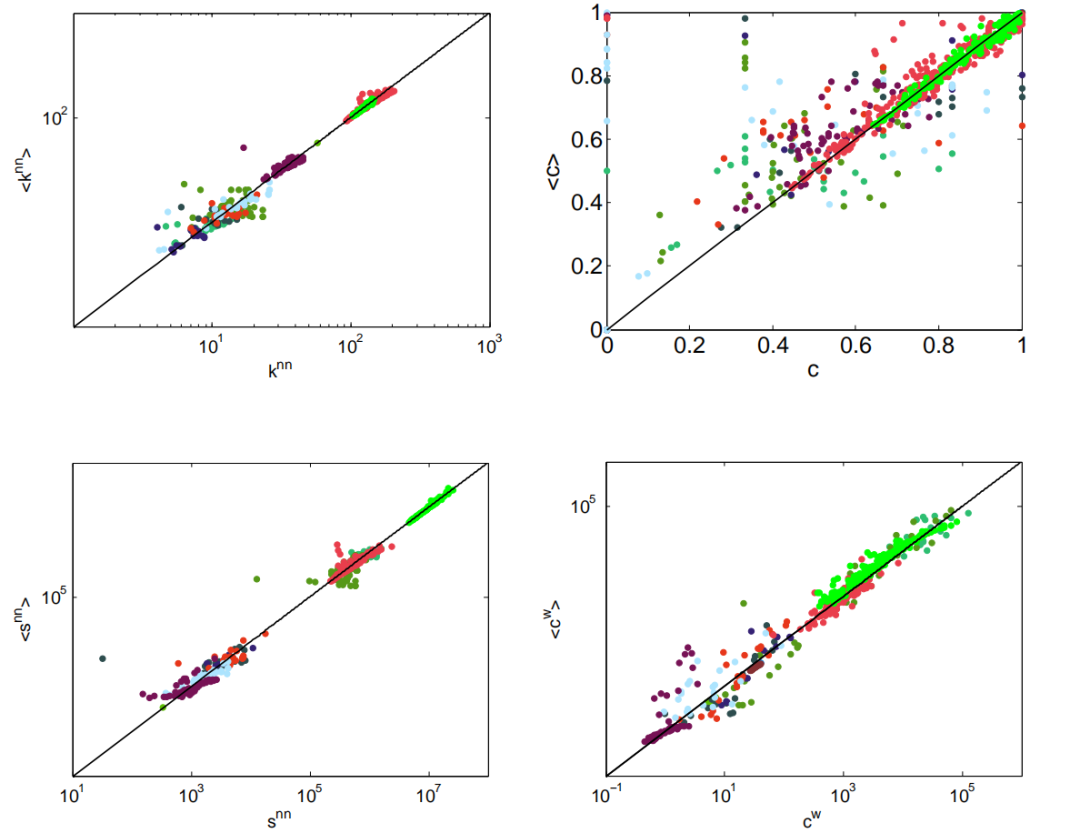
宏观尺度上的网络重构侧重于推断网络的全局特征，例如同配性和层次结构。在研究该尺度时，通常不考虑任何特定拓扑细节，而是利用网络的多种宏观属性来指导重构。

主流的宏观尺度网络重构模型有 2011 年提出的 Directed Weighted Configuration Model[1]和 2018 年提出的 Maximum-Entropy Capital Asset Pricing Model（MECAPM） [2]。在描述网络性质的众多参数中，Strengths（节点所有连边的权重和）发挥了很重要的作用，因为它是很多实际网络能提供的唯一信息。遗憾的是在仅提供 Strengths 信息的情况下，以上两种方法都无法很好地重构网络宏观结构。2014 年提出的 Enhanced Configuration Model（ECM）[3]则可以很好地解决该问题。下图为 ECM 在宏观尺度网络重构中的表现。

图1. 已知 srengths 和度的情况下，ECM 模型的表现。每张子图都展示了针对某些网络实际节点特定网络属性的重构结果（Y轴）与理论值（X轴）左上：最近邻居平均度（average nearest neighbors degree），右上：集聚系数(clustering coefficient) ，左下：最近邻居平均强度（average nearest neighbors strength），右下：加权聚类系数（weighted clustering coefficient）[3]

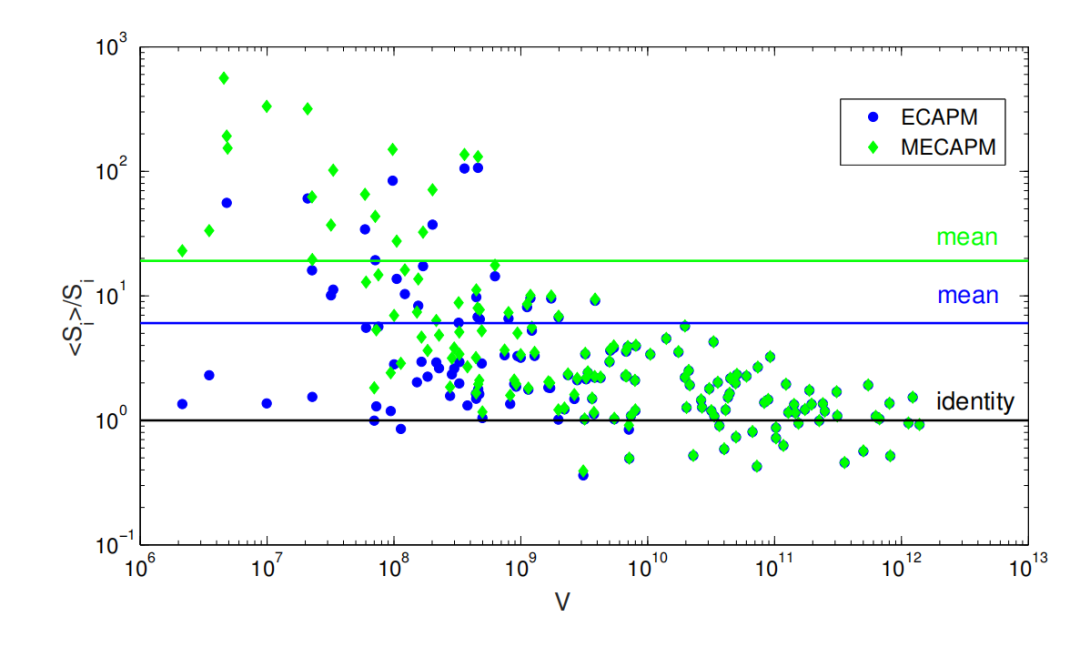
为了从另一个方面分析重构方法的优缺点，该综述还讨论了系统风险的量化问题。自金融危机爆发以来，这个问题变得极为重要。金融机构之间复杂的互连模式有可能使整个系统变得极为脆弱，因为这些联系构成了财务危机扩散的渠道，这是金融系统风险的主要来源。下图为 dcGM[4] 和 MECAPM[2] 两种模型在证券持有（SHS）网络上的表现。

图2. 在 SHS 网络数据集中重构网络系统性:每个点代表一个具体部门使用dcGM（蓝色）或MECAPM（绿色）推断出的相对系统性，两种方法的平均值均以水平实线表示。[14]

2. 介观尺度的网络重构

介观尺度的网络重构侧重于发现节点分布模式，如社区结构、核心-边缘结构和二分结构，并以此指导网络重构。该主题引起了流行病学、生物学等领域的关注，并最终确定核心问题为发现节点间连接的模式及其衍生功能的相似性。介观尺度模式的存在对于网络上的各种动态过程，如信息和流行病的传播有巨大影响。

2.1 社区结构

如图 3 所示，满足社区结构的网络由多个结构相似的模块组成。社区发现问题有多方面价值：首先，同一社群的节点具有很多相似的属性，因而可以用于指导网络的粗粒化从而简化数据规模。其次，具有不同属性的社群有助于揭示在宏观尺度下被平均化的网络特征。此外社区划分还可以指导对于模块功能的探索等。

图3. 网络的社区结构举例及其邻接矩阵表示[5]

社区检测问题仍然是一个未解决的问题，在过去二十年中有许多算法陆续被提出，主要可以分为两大类：局部社区检测和全局社区检测。局部社区检测基于社团内部的属性，例如度、可及性和凝聚性等。当网络的全局信息需要纳入考虑时，则需要使用全局社区检测方法。十分流行的模块度方法就属于全局社区检测。

2.2 核心-边缘结构

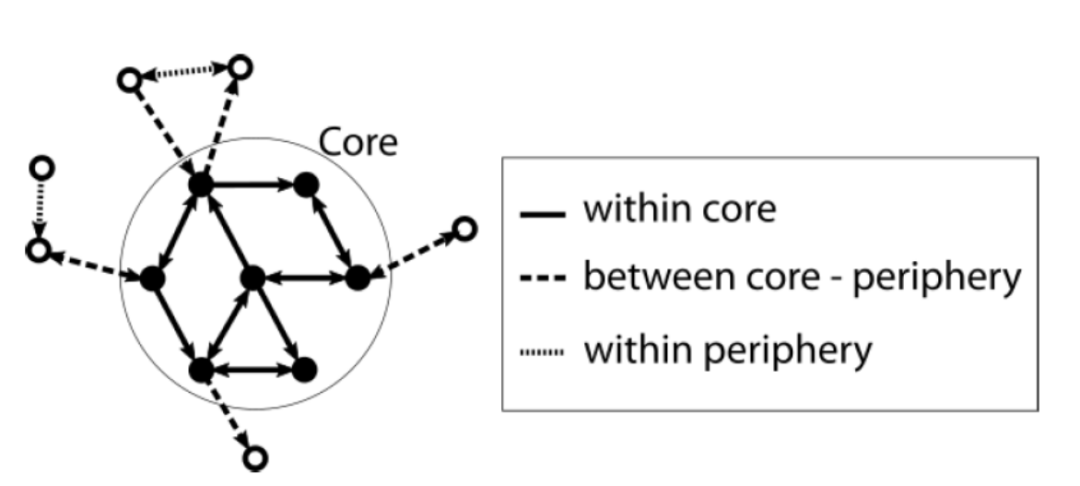
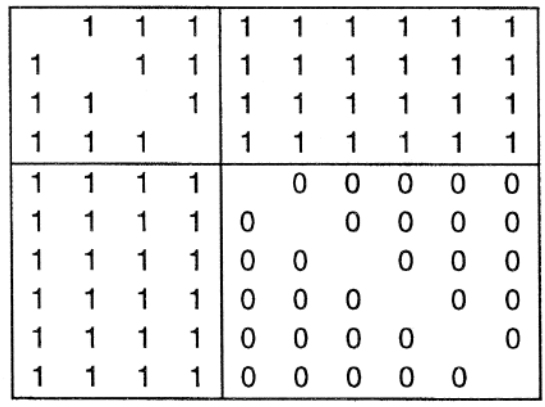
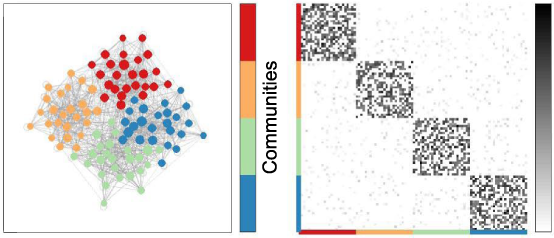
如图 4 所示，满足核心-边缘结构的网络由大量紧密链接的核心节点和稀疏连接的外围节点组成，该类型的网络在经济学、社会学、神经科学等领域广泛出现。

图4. 核心-边缘结构网络示例左图为核心-边缘结构网络中的节点类型，右图为严格符合核心边缘结构的网络的邻接矩阵[6]

第一个不以网络一定具有核心-边缘结构为前提的检测算法由 Holme 在 2005 年提出[15]，该算法主要基于网络的紧密中心性。2013 年由 Della Rossa 等人提出的基于标准随机游走的算法将检测范围扩充到了加权网络[16]。在最近的研究中，van Lidth de Jeude 等人受超几何分布中的 p 值启发提出了一种新的核心-边缘检测基准模型[17]。

3. 微观尺度的网络重构

微观尺度的网络重构重点在于预测网络中缺失的具体连边，即链路预测问题。该问题对于多种具体网络都有重要价值。以生物领域为例，对于食物网、蛋白质相互作用网和代谢网络而言，通过实验来判断节点间是否存在连接需要付出巨大的经济成本。与其盲目进行实验，不如先通过链路预测找到那些最有可能存在的连边，而后有的放矢地进行试验。

链接预测方法大致可分为两大类：基于相似度的算法和基于模型的算法。两种方法的关键基本假设均为：如果两个节点具有更大的相似性，则它们之间更可能存在链接。

3.1 基于相似度的算法

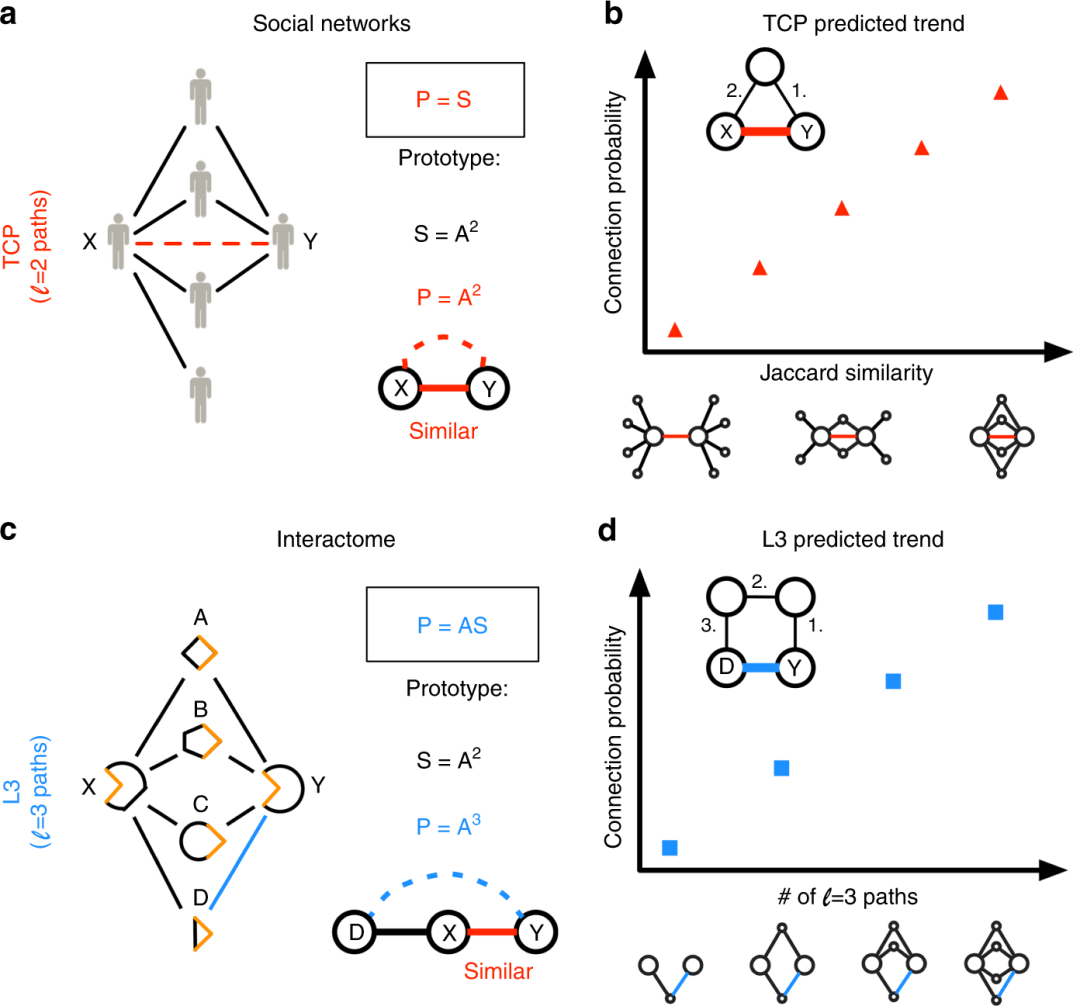
基于相似度的算法为每个待预测的连边生成一个分数来评价其连接节点间的相似性。该分数取决于节点间属性的差异性。依照所用节点属性还可以将算法具体分为基于局部、半局部和全局相似性的算法。

如图 5(a) 所示，基于局部相似性的算法通常基于社交网络分析中的共同邻居观念，即如果两个人的共同朋友越多，他们彼此认识的可能性就更大，该原理被称为三元闭包（Triadic Closure Principle），是网络中长度为 2 的路径产生的主要原因。半局部相似性则与网络中长度为 3 的路径更为相关，例如在蛋白质相互作用网络中，两个结构相似的蛋白质不会相互作用。如图 5(c) 所示，当蛋白质D与Y被很多长度为3的路径连接时，二者才更有可能产生一条连边。

图5. 社交网络与蛋白质网络中的链路预测图a为社交网络中连边产生的示意图。图b为在满足三元闭包原理（Triadic Closure Principle）的网络模型下不同状态的节点对间产生连边的概率。图c为蛋白质相互作用中连边产生的示意图。图d为在满足四元闭包原理（Quadrangular Closure Principle）的网络模型下不同状态的节点对间产生连边的概率。[7]

3.2 基于模型的算法

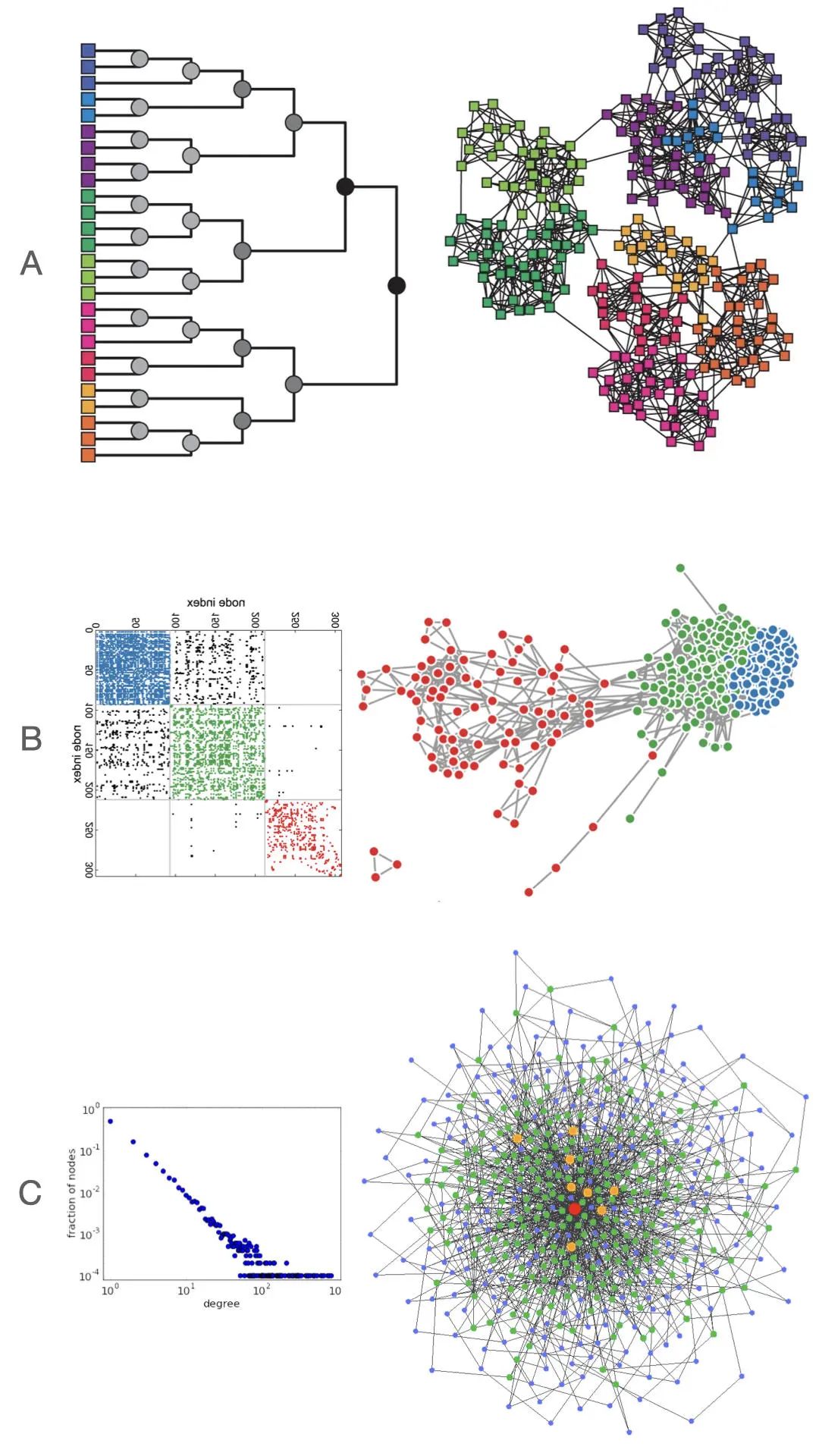
基于模型的方法构建于网络具有特定组织结构的假设之上，如图 6 所示，该类算法希望待预测的连边可以尽可能好地完善网络所具备的结构。

图6. 在基于模型的算法上对网络结构进行采样（A）分层结构网络（B）块状结构网络（C）无标度网络[8-10]

以层次结构模型为例，该类算法基于现实世界中许多网络是分层组织的，这意味着可以将节点划分为组，随后再细分为组的组，以此类推。利用提取出的层次结构辅助链路预测。2008 年由 Clauset 等人提出的 Hierarchical Random Graph Model[8] 是具有代表性的基于层次结构的模型。该模型给网络中的每个节点定义了一个连接概率，两个节点间是否存在连边取决于二者共同父节点的连接概率。

4. 小结

在大数据时代，人们对于数据完整性的需求愈发提高，网络重构技术可以在信息提取质量不高的情况下，从数据本身出发最大程度的恢复数据完整性，具有广阔的应用场景。

这篇综述从宏观、介观、微观三个角度介绍了网络重构领域的研究问题、常见模型及应用场景。到目前为止，网络重构领域处于快速发展和完善的阶段，有向加权图上的链路预测[11]、对于连边具有信息的网络的重构[12]以及时序网络重构[13]等研究方向正在快速发展。

参考资料

[1] Squartini, Tiziano and D. Garlaschelli. “Analytical maximum-likelihood method to detect patterns in real networks.” New Journal of Physics 13 (2011): 083001.

[2] Gangi, Domenico Di et al. “Assessing Systemic Risk Due to Fire Sales Spillover Through Maximum Entropy Network Reconstruction.” Regulation of Financial Institutions eJournal (2018): n. pag.

[3] Mastrandrea, R. et al. “Enhanced reconstruction of weighted networks from strengths and degrees.” New Journal of Physics 16 (2014): 043022.

[4] Cimini, G. et al. “Systemic Risk Analysis on Reconstructed Economic and Financial Networks.” Scientific Reports 5 (2015): n. pag.

[5] Faskowitz, J. et al. “Weighted Stochastic Block Models of the Human Connectome across the Life Span.” Scientific Reports 8 (2018): n. pag.

[6] Borgatti, S. and M. Everett. “Models of core/periphery structures.” Soc. Networks 21 (2000): 375-395.

[7] Kovács, István A. et al. “Network-based prediction of protein interactions.” Nature Communications 10 (2019): n. pag.

[8] Clauset, A. et al. “Hierarchical structure and the prediction of missing links in networks.” Nature 453 (2008): 98-101.

[9] Larremore, D. et al. “A Network Approach to Analyzing Highly Recombinant Malaria Parasite Genes.” PLoS Computational Biology 9 (2013): n. pag.

[10] Oikonomou, Panos and P. Cluzel. “Effects of topology on network evolution.” Nature Physics 2 (2006): 532-536.

[11] Alon, U.. “Network motifs: theory and experimental approaches.” Nature Reviews Genetics 8 (2007): 450-461.

[12] Leskovec, J. et al. “Predicting positive and negative links in online social networks.” WWW ’10 (2010).

[13] Tylenda, Tomasz et al. “Towards time-aware link prediction in evolving social networks.” SNA-KDD ’09 (2009).

[14] Squartini, Tiziano et al. “Enhanced capital-asset pricing model for the reconstruction of bipartite financial networks.” Physical review. E 96 3-1 (2017): 032315 .

[15] Holme, P.. “Core-periphery organization of complex networks.” Physical review. E, Statistical, nonlinear, and soft matter physics 72 4 Pt 2 (2005): 046111 .

[16] Rossa, F. et al. “Profiling core-periphery network structure by random walkers.” Scientific Reports 3 (2013): n. pag.

[17] Jeude, J. V. L. D. et al. “Detecting Core-Periphery Structures by Surprise.” ArXiv abs/1810.04717 (2018): n. pag.

课程推荐