PRL：找寻网络中的创新“守门员”

导语

不断的探索新知，需要人与人之间的交流，即社交网络构建了我们人际交往的基础。发表于12月份 Physics Review Letters 的一篇论文将波利亚瓮模型扩展到复杂网络，发现个体在网络中所处的位置，对于整个网络的创新能力影响更加显著。
郭瑞东 | 作者
赵雨亭 | 审校
邓一雪 | 编辑

论文题目：
Interacting Discovery Processes on Complex Networks
论文地址：
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.248301

1. 创新与社交网络密不可分

今年6月发表于 Physics Review Letters 的一篇论文[1]展示，在基于对大学物理课程的实地调研中发现，对于开放式问题，处于社交网络中守门员（gate keeper）位置的个体——即连接不同子网络的关键节点——更容易得到创新答案。例如下图中的节点 F，就是本网络中连通绿色、橙色和蓝色子网络的守门人。

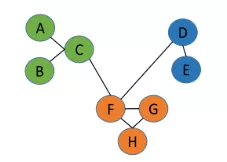
图1. 网络中守门员（gate keeper）示意图

而如果希望定量地研究创新与社交网络的关系，就需要先建立模型，再进行计算机模拟。如果需要将未知的概念看成由已知概念经由一次跳跃就能达到的产物，则可以使用波利亚瓮模型（Polya Urn）来描述发现新知识的过程。

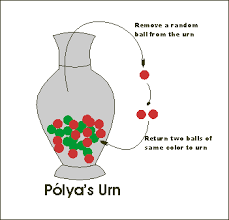
图2. 波利亚瓮模型包含 X 白球和 Y 黑球：从瓮（urn）中随机抽取一个球，观测其颜色后，将其返回瓮中，并且将相同颜色的球加入其中；重复该过程。

基于波利亚瓮模型对创新活动进行建模，能够刻画出创新所具有的正反馈，即新的知识会扩展模型可能性边界，从而使其后的探索变为可能。该模型能重现语言中的统计规律，如 Zipf 法则（见图3）。由于语言反映了知识的积累，因此模型中展现的类似规律，可说明波利亚瓮模型能够反映真实世界中的知识发现过程。

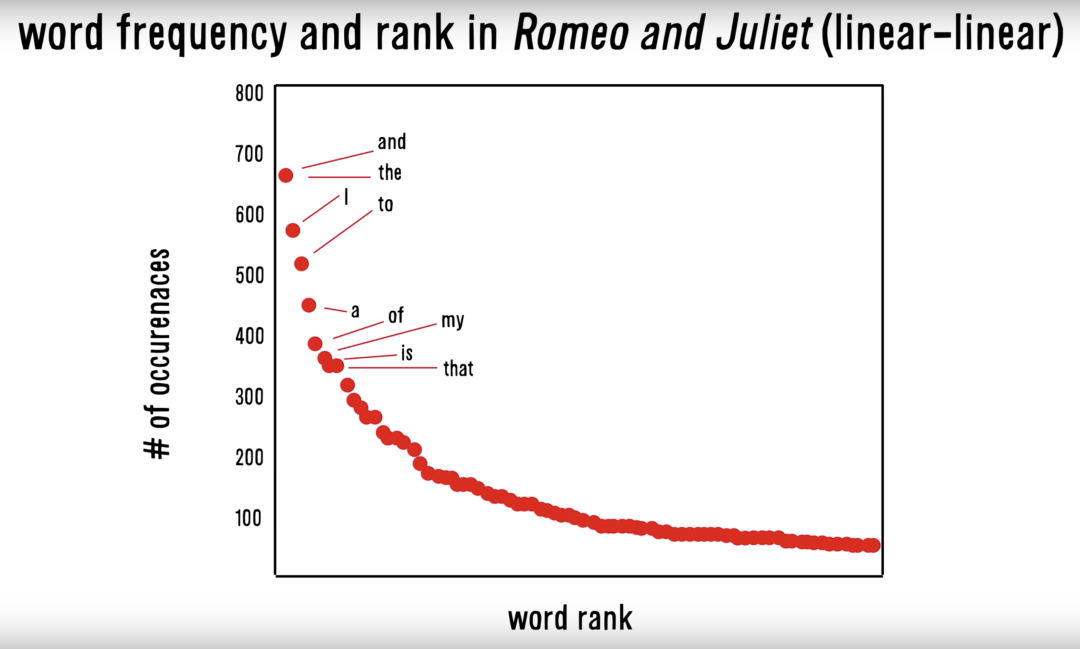
图3. Zipf 法则：指自然语言中，一个单词出现的频率与它在频率表里的排名成反比。即幂律法则在自然语言中的体现。

然而，单个的瓮只能反映每个人独自探索未知的过程——与真实世界中，探寻新知的人组成社交网络、每个人处在网络中的不同结构这一特点相矛盾。同时真实世界中的知识发现也非依赖已实现定义的网络结构，而是由知识探索的过程动态决定的。

在基于社交网络的波利亚瓮模型中，网络中的每个节点从一个公共的瓮中抽取附带各自标签的小球（每回合可选的小球，包含之前回合抽取后放入的小球）。如图4所示，新加入的球扩展了可选小球的范围（更多颜色），对应创新带来更多的创新。

图4. 不同节点对应的瓮的状态演化示意图

波利亚瓮模型不同于传统针对传染病或信息扩散的建模。传统模型中，网络只起到了调控哪些信息能够传播的作用，不会影响网络中的每个节点如何选择、有哪些选项。在波利亚瓮模型中，知识创新的过程既包含个人的选择，也受到社会的动态发展制约。相较传统模型更为接近真实情况。

2. 通过Heaps法则，
判定发现新知识的积累速度

自然语言中，文本长度和文本中包含的词汇量呈亚线性关系，即公式 VR (n)=Knβ 中的 β 小于1。Heaps 法则如下图所示，图中横轴是文本长度 m，纵轴是文本包含的词汇总数 V，公式中的 K 与 β 是可变参数。如果 β 越大，那么同样长度的文本包含的新词汇就越多。

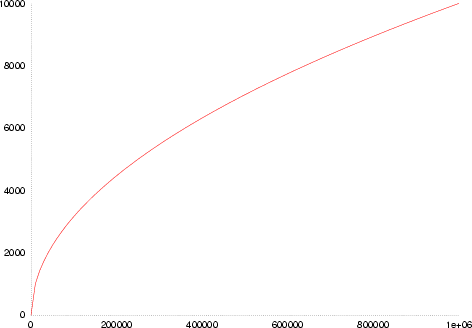
图5. Heaps 法则示意图：文本长度与文本对应词汇的对应关系

在本文提出的波利亚瓮模型中，每组文本可看成瓮中的球对应的标签集合，即探索新知的成果。如果探索过程中新词汇的增速相对较快，则 heaps 法则中的 β 值更高，即反映了该节点发现新知识的能力更强。

下图展示了社区网络结构中常用的空手道俱乐部网络（Zachary karate club network，ZKC）在波利亚瓮模型中的表现，图中颜色越深的小球代表该节点发现新知识的能力越强，其中1号节点代表俱乐部中的导师，34号节点是俱乐部管理者，两者都处在网络中连接不同子网络的关键位置，且这两个节点在模型中对应的 β 也越大，说明模型是真实世界的成果体现。

图6. 空手道俱乐部网络中，展示不同节点影响力的 Heaps 模型的示意图

3. 分享越多，知识积累越快

该研究最有意义的部分，是根据模型，讨论了在网络中处于怎样的结构更有利于快速地探索出更多的新知。接下来分4步，逐条介绍波利亚瓮模型得出的、关于知识发现的规律。

波利亚瓮模型中，每个节点抽取一个球，其颜色代表了某个概念，放回小球的过程代表对这个概念更深入的了解，这个动作改变下一步抽取小球的可选项。如果存在节点A到B的有向边，意味着节点B可以使用节点A之前发现的概念，扩展B自身可选项。

下图代表模拟实验中，节点所具有的、以该节点起点连边的数量，以及对应节点的已探索概念的数量变化过程（中图）与 Heaps 定律中的 β 值。可以看出，连边数目越大，β 值越高、同样时间内发现的新知越多。这不难理解——通过向更多人分享你的发现，你相当于让其他人帮助你发现新知，从而加速知识发现的过程。

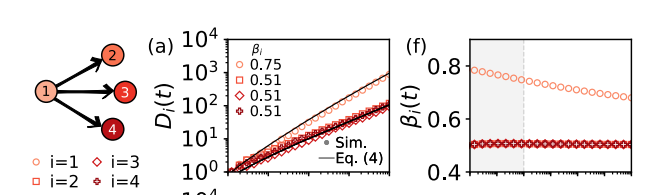
图7. 左图中的节点1有三条出边，其它节点都没有出边。不同的形状代表图示对应的不同节点。模拟中，节点1遵循 Heaps 法则，其中 β 值随时间变化幅度大于其它节点（右图），其概念集合的增速也更快（中图）

4. 发现过程中，第一手信息更重要

‍一组人共同探索新知，节点2探索的可选项，来自节点1的发现知识，节点3的可选项又来自节点2发现的知识集合。在这样的网络中，发现新知最快的是节点1，如下图所示。从这里可以引申得出，知识探索过程中，第一手信息更为重要。

图8. 链式网络中的节点先后位置决定发现知识的速率

5. 波利亚翁模型得出的知识发现的规律3:
网络中的环状结构会加速知识发现

如果网络中包含环状结构，那么处于环中的每个成员，都将以更快的速度发现新知。即包含环的图结构中，部分节点的 β 值大于之前两种情况下任意节点的 β 值——例如下图c的所有节点和e中除1以外的节点。这意味着社交网络中紧密联系的小群体会加速群体的知识探索过程。

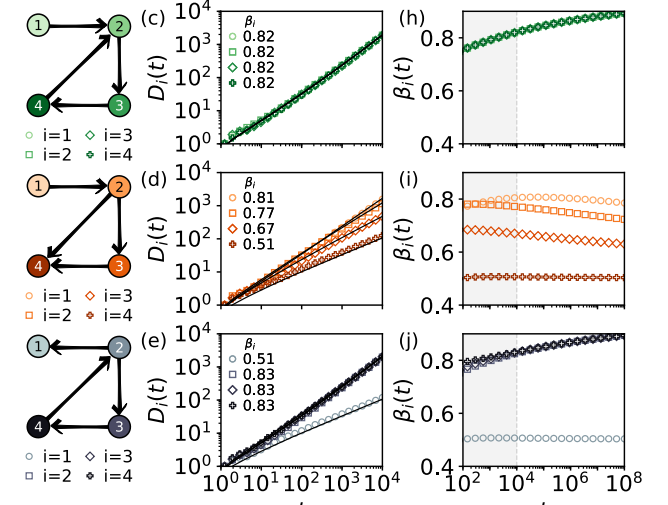
图9. 包含环的网络中的节点其对应的 β 值相比之前的网络结构更高

上图c中，每个节点的知识发现顺序都相近——尽管节点1只有一条出边，但由于节点234组成了环，使得234中任意一员实际上都等效于其余节点。图e和图c的差异在于节点1和2之间连边的方向，而这导致了节点1的知识发现过程显著减速；图d中节点4只有入边，没有出边，这导致了不同节点的知识发现效率有所不同。

6. 处在社交网络的中心，能更快地发现新知

在前文提到的空手道俱乐部网络中，在网络里不同结构的成员对应的 β 值不同。将节点的特征向量中心度标准化之后，可以发现中心度与知识发现的能力呈强相关关系。

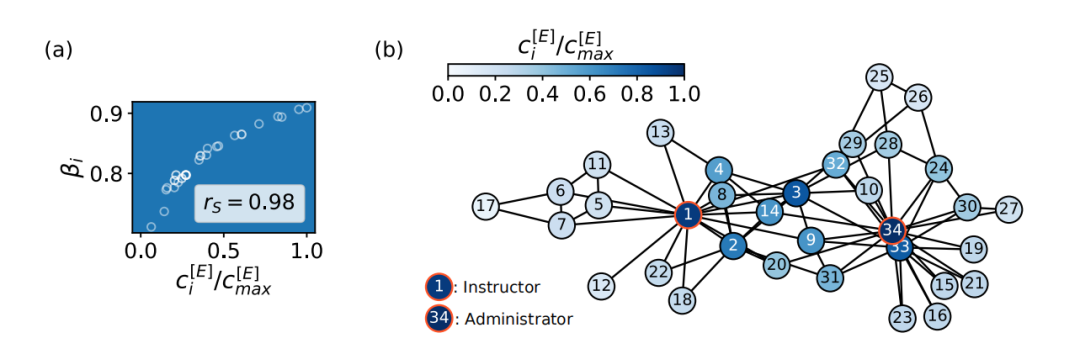
图10. 来自补充材料，右图是节点的特征向量中心度，颜色越深，中心度越高，左图是节点中心度和对应β值的散点图，其斯皮尔曼相关系数（衡量两个变量依赖性的非参数指标）为0.98

而在真实的大规模网络（如推特、科研论文共同作者、或共同表演搭档的爵士音乐家网络）中，都出现了类似的规律，如图11所示——这意味着处在社交网络的中心，能更快地发现新知。

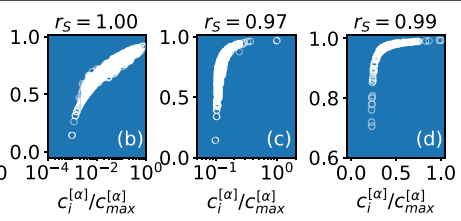
图11. 真实网络中，节点中心度和 β 值的散点图

7. 总结

该文首次将波利亚瓮模型和复杂网络结合起来，用来对知识探索这一基于社交网络的过程进行建模，模型重现了真实场景中的规律——如 heaps 法则——将社交互动引入对创新过程建模的第一步，之后可以给节点增加记忆限制（如新加入的知识会带来旧知识的遗忘），从而使模型具有更多层次；或将模型放在多层网络中，抑或考虑网络高阶拓扑结构带来的影响。

该论文的第二点启发，是指出波利亚瓮模型可以用来描述并建模诸如迷因传播、技术扩散等基于社交网络的现象。此外，该论文重点关注的是网络中处在不同结构的节点发现新知识的能力，将不同特征的社交网络看成一个整体，其后可以经由模型，重现解释及预测诸如国家或企业创造新知识的能力差异，这是未来相关研究的另一个可能的方向。

参考资料
1，Social networks and academic performance in physics: Undergraduate cooperation enhances ill-structured problem elaboration and inhibits well-structured problem solving

复杂科学最新论文

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：