PRE：武装冲突的幂律法则

导语

为什么在武装冲突中，越严重的冲突，发生的几率越低？新研究根据近三十年来非洲武装冲突的情况，对此给出了解释。
郭瑞东 | 作者
赵雨亭 | 审校

邓一雪 | 编辑

论文题目
Scaling theory of armed-conflict avalanches
论文地址
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.102.042312

1941年，物理学家 Lewis Fry Richardson 通过分析历史中冲突中的死亡数据，发现冲突的严重程度与冲突发生的频率之间符合幂律法则关系，这表明较小冲突是较大冲突的缩小版本，但迄今为止，还没有对为什么会在武装冲突中，幂率法则同样适用的情况给出可信服的、系统的解释。

圣塔菲研究所集体计算小组的 Christopher Meyers 使用来自非洲武装冲突的数据来解释冲突是如何在一个地理区域蔓延的，该模型描述了暴力活动如何相互作用，验证了暴力冲突在时间和空间上如何以无标度的方式成长和扩散。

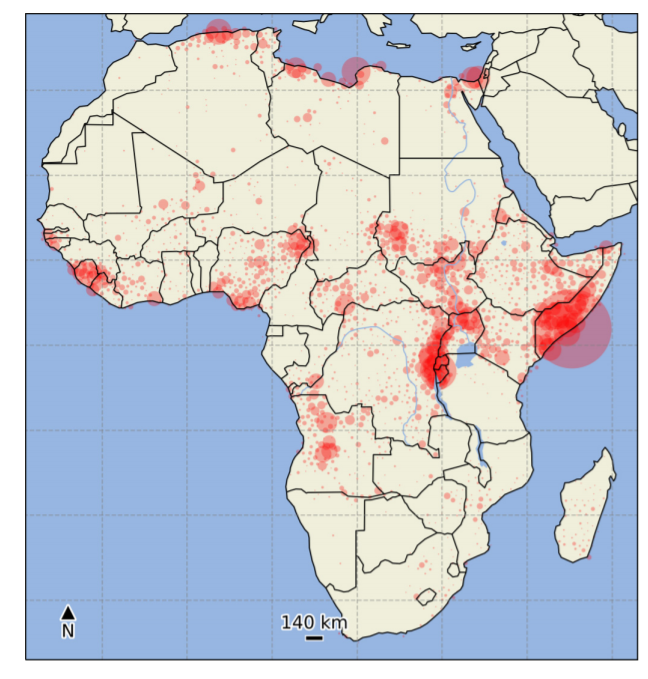
图1. 该文中用到的近二十年非洲报道的武装冲突的位置，死亡人数及时间汇总图，包括100,000个发生在数千公里范围内发生的事件

该模型被命名为随机分叉的武装冲突（ randomly branching armed conflict）模型。在该模型中，当一个地区发生武装冲突后，会随机地带动相邻的区域发生烈度更低的冲突，最终的冲突演化效果类似具有分形特征的树杈。

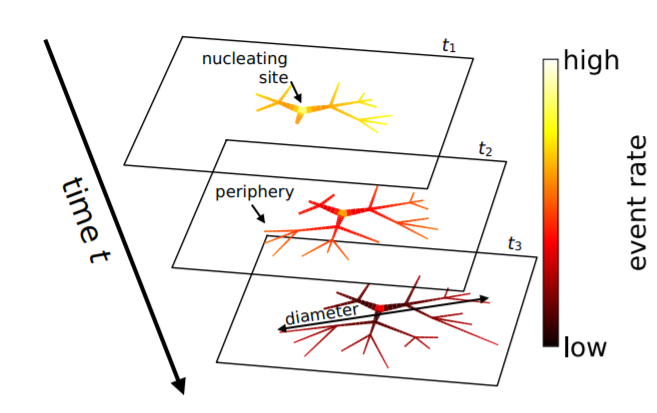
图2. RBAC模型示意图，图中线条越粗，总的冲突次数越多，因此最初发生冲突的区域的最粗

每一条冲突分支中，任意一个具体的冲突，都是特定社会和文化动态的结果。具体汇总分析之后，可以发现事实上这些看似不同的冲突其实是同一种模式的拥有的共同属性，通过识别出具体冲突背后的统一的原则，可以展示暴力冲突如何通过时间和空间传播，物理尺度（距离）与冲突报告和死亡人数密切相关，从而揭示了暴力在地理和社会层面是如何交织在一起的。

如果你在一堆沙子中倒入足够多的沙子，沙子的两侧最终会变得非常陡峭，以至于一粒新的沙子就可以引发一场雪崩。然而，由于崩塌，斜坡变平了，堆积可以再次发生。如果森林中的树木生长得足够茂密，它们就能使雷击引发的火灾迅速蔓延，清除森林。待到新生森林再次达到临界密度，上述的规律再一次重复发生。

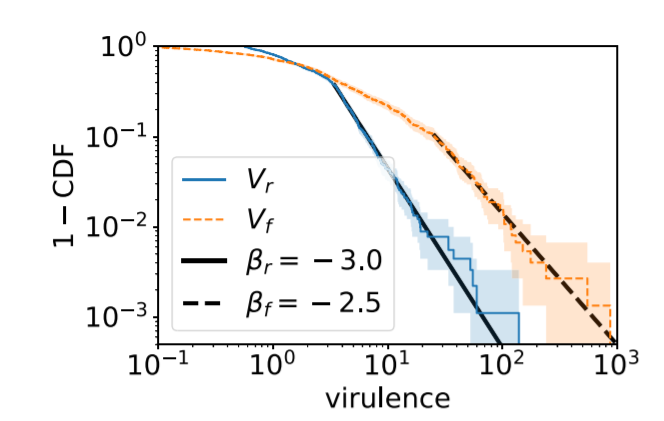
图3. 武装冲突在发生之初，需要达到临界质量，之后遵循幂律法则

本项研究发现，上述规律也适用于武装冲突，这意味着一个地区会聚集一些压力，最终会看到一连串的武装冲突。级联效应可以解释冲突爆发在不同地区和时间存在的巨大差异，为什么一些冲突很快消失，而另一些则引发了长期的冲突。该工作还解释地区差异的必要性。与其他地区相比，不仅某些地区的冲突更加频繁和激烈，而且冲突强度的空间差异本身可能遵循一个标度律。

武装冲突中的规律，让对幂律法则熟悉的读者，想到城市中的创新和犯罪如何与城市人口规模相匹配——通过研究不同幂律法则的异同，或许可以回答“我们在武装冲突中看到的模式如何与我们在其他地方看到的其他模式相联系？”这个问题。

参考资料：https://www.santafe.edu/news-center/news/avalanche-violence-new-analysis-reveals-predictable-patterns-armed-conflicts

复杂科学最新论文

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：