复杂性科学论文推荐7篇 | Complexity Express一周精选2.1-2.7

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。

扫描下方二维码，关注“集智斑图”服务号，即可订阅Complexity Express：

Complexity Express 一周论文精选

以下是2021年2月1日-7日来自Complexity Express的复杂性科学论文精选。如果Complexity Express列表中有你感兴趣的论文，欢迎点赞推荐，我们会优先组织解读~
目录：
利用拉马努金机生成基本常数的猜想
使用解扰器组进行神经网络解释
基于经典力学的高性能组合优化算法新冠肺炎危机带来生活水平下降：来自9个发展中国家的海量数据证明白蚁巢穴的自组织生物构造社会科学的黄金时代大型金融数据中赌博与财务、社交以及健康之间的关系

1.利用拉马努金机生成基本常数的猜想
期刊来源：Nature

论文题目：Generating conjectures on fundamental constants with the Ramanujan Machine论文网址：https://www.nature.com/articles/s41586-021-03229-4

e和π这样的基本常数大家肯定都不陌生，它们的身影遍布数学、物理、化学、生物等多个科学领域。但几个世纪以来，基本常数并不常见，而且往往伴随着偶然或依赖科学家的直觉。为打破这种瓶颈，2021年2月3日 Nature 上发表的一篇文章提出利用算法得到基本常数的数学公式猜想并揭示常数的基本结构，即“拉马努金机”（Ramanujan Machine）。目前，拉马努金机可以用连分数（continued fraction）形式表示几十个耳熟能详的公式（如π、e等）和以前未知的公式。该研究提出两种具体实现的算法，分别是“中间相遇法”（The Meet-In-The Middle）和针对连分式递归结构的梯度下降优化算法。这两种算法都基于数值匹配，因此不需要提供任何关于基本常数的先验信息，后者还可以一定程度上弥补中间相遇法扩展性不佳的问题。这一研究成果支持了一个全新的研究框架——不再依赖伟大数学家的直觉，而是利用AI技术来揭示数学结构，并为未来数学研究开辟了新角度。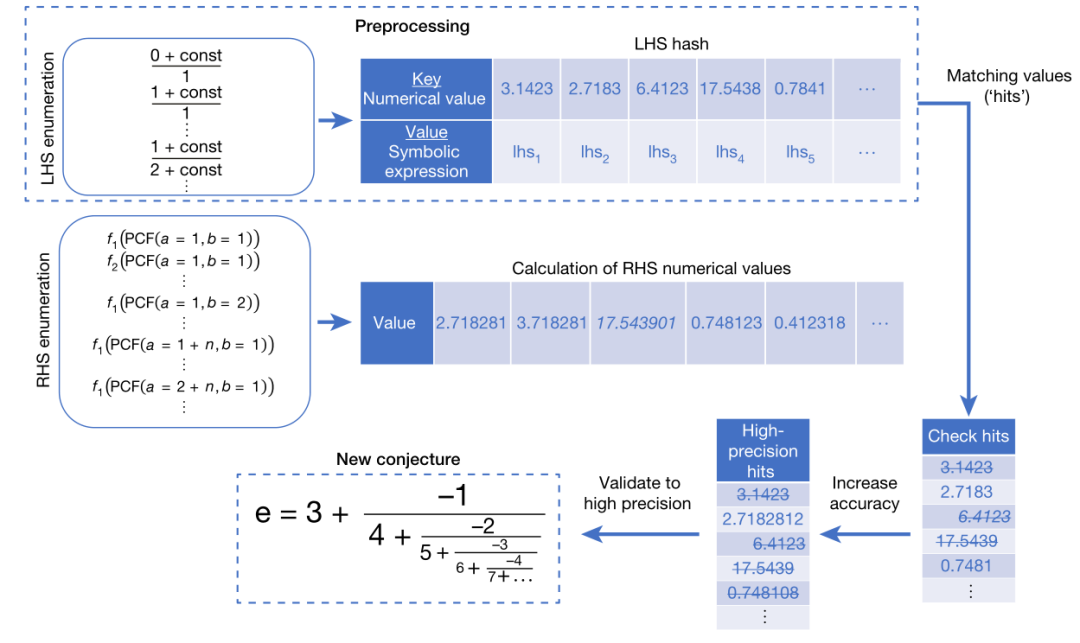上图为“中间相遇法”（The Meet-In-The Middle）算法流程

2.使用解扰器组进行神经网络解释
期刊来源：PNAS
论文题目：Neural network interpretation using descrambler groups论文地址：https://www.pnas.org/content/118/5/e2016917118
缺乏可解释性是深度神经网络的一个重要缺陷。在全连接神经网络中，层与层之间传递的信号在我们眼中是混乱的，因为反向传播算法无需感知机以任何特定规律排列。该问题在科学计算与数字信号处理（DSP）中尤为严重，在这些工作中，神经网络运行的抽象数学变换无法简化为具体的特征或概念。2月2日发表在 PNAS 上的一篇文献在神经网络具有可解释性的假设基础之上，提出了一种将神经网络各个层输出信号转化为人类可读形式的方法。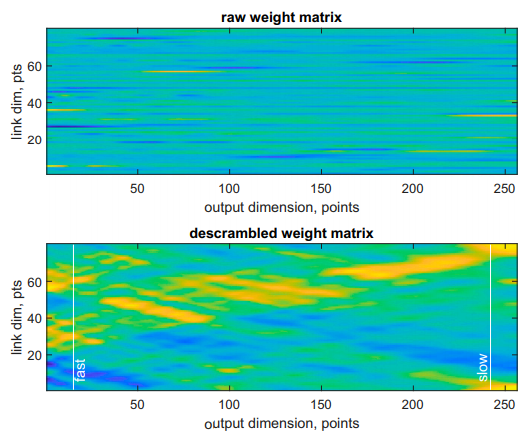
在DEERNet的第二个全连接层的权重矩阵中自发出现了时间-距离变换。上图为原始权重矩阵，下图为经过解扰变换后的输出。
该方法将神经网络各个层的权重矩阵进行特定的线性解扰变换（”descrambling” transformation），使其输出对有背景知识的人是可读的。作者将该方法应用于DEERNet（一种用于电子自旋共振的DSP网络）发现其内部机制十分复杂，在十分钟的训练后，神经网络中自发地出现了带通滤波器、陷波滤波器、组嵌入等多种精细结构。 3.基于经典力学的高性能组合优化算法
期刊来源：Science Advances
论文题目：High-performance combinatorial optimization based on classical mechanics论文地址：https://advances.sciencemag.org/content/7/6/eabe7953

组合优化问题在各种社会与工业问题中十分常见，因此快速解决此类问题具有重要意义。然而，随着优化问题规模的不断增大，决策变量取值的不同组合量、可行解数量以及寻找最优解时需要考虑的组合量也会迅速大幅度增加，且往往是以指数形式增加，最终导致无法从中快速找到最优解。最近已经提出了一种名为模拟分叉（simulated bifurcation，SB）的量子启发算法，以加速组合优化，该算法的优势在于可以使用GPU进行大规模并称处理。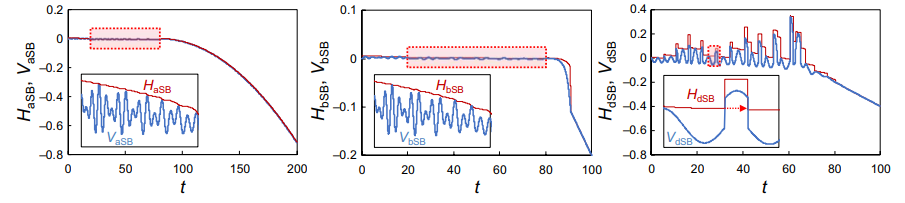
使用aSB，bSB，dSB解决双自旋铁磁伊辛问题。上图为三种算法下势能、总能量与时间的关系。（插图为红色矩形区域的放大）
目前已有的结果表明SB算法可以快速地找到近似解，但尚不清楚SB算法是否可以找到大规模问题的最佳解决方案。2月3日发表在 Science Advances 上的一篇文章在原有的绝热SB模型（aSB）基础上引入了ballistic SB（bSB）与离散SB（dSB）两个变体。在多个问题上对bSB、dSB与其他热门算法进行了比较，最终发现dSB具有更好的性能。
4.新冠肺炎危机带来生活水平下降：
来自9个发展中国家的海量数据证明
期刊来源：Science Advances
论文题目：Falling living standards during the COVID-19 crisis: Quantitative evidence from nine developing countries论文网址：https://advances.sciencemag.org/content/7/6/eabe0997

新冠肺炎席卷全球，对各国的经济活动带来不同程度的冲击，居住在低收入或中等收入国家中的弱势居民更容易面临严峻的生计威胁。2021年2月5日发表在 Science Advances 上的一篇论文了收集来自非洲（布基纳法索、加纳、肯尼亚、卢旺达、塞拉利昂)、亚洲(孟加拉国、尼泊尔、菲律宾）和拉丁美洲（哥伦比亚）9个国家、3万多户家庭数据，对COVID-19对中低收入国家各群体的经济影响进行充分的数据分析。结果显示：从2020年4月以来，这9个中低收入国家的就业率、居民收入和食品安全质量显著下降。在这种情况下，大多数人依靠临时工作赚取杯水车薪，这也引发了大范围的贫困，甚至会导致未来过高的发病率、死亡率和其他不良后果。另一方面，COCID-19带来的经济困局带来了更加严重的温饱问题，饥饿使社会生产力和经济长期增长面临风险。值得注意的是，疫情导致的贫穷与饥饿现象大幅减少了对于儿童健康和教育的投资，从长远来看会严重影响社会福祉和发展。该研究根据数据分析结果讨论可能的政策应对措施，并预测持续不良影响的风险。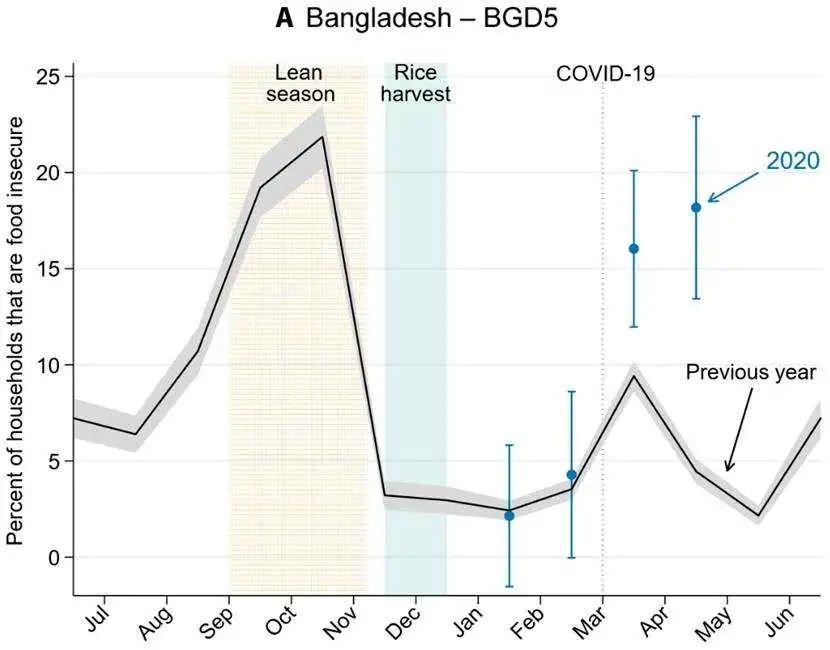图为孟加拉国北部无地农户的每月粮食不温饱率情况。食物不温饱的定义是一个月至少有15天没有吃饭或减少食物的分量。

5.白蚁巢穴的自组织生物构造
期刊来源：PNAS

论文题目：Self-organized biotectonics of termite nests论文地址：https://www.pnas.org/content/118/5/e2006985118

白蚁巢是动物社会产生的最复杂和令人印象深刻的结构之一——它们创建了一个微生态位，使得物质和能量与环境的交互在可控条件下进行。自然界中，其它某些动物也表现出了集体行为（包括协调运动，主动同步或共同决策）——但与它们相比，社会性昆虫——如高度真社会性（Eusociality）的白蚁——的集体活动大相径庭：它们常常可以形成复杂的物理结构——如庇护所、追踪网络；尤其最引人注目的是巢穴。但是，这些结构不仅是白蚁行为的副产品，同时它们在调节自身构造和功能所需的信息流方面也起着核心作用。因此，在社会性昆虫中，筑巢被视为是功能性自组织的典范。研究这一过程可以使我们了解生态生理学中结构和功能的出现方式。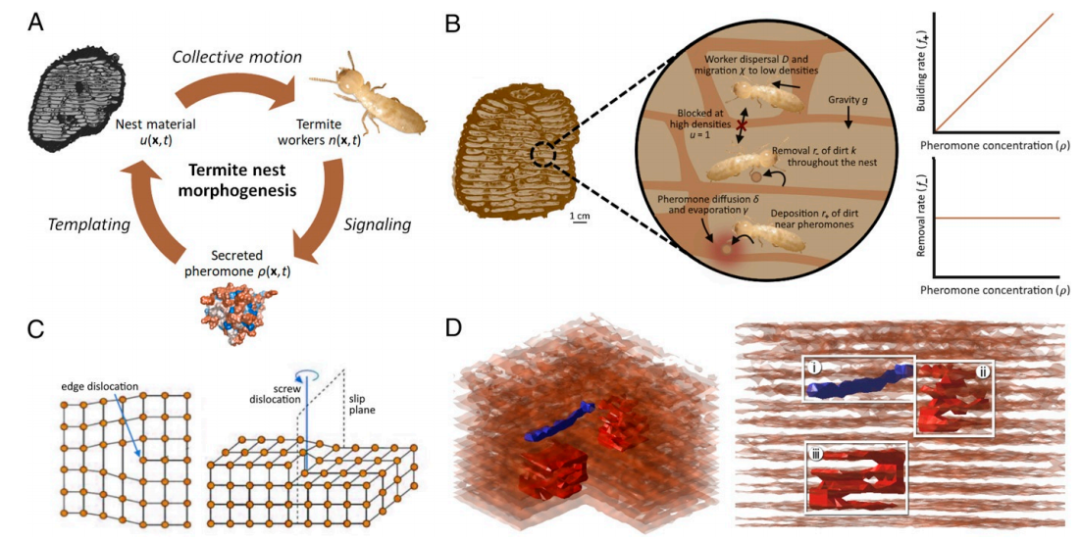生物构造模型可预测白蚁巢内的每层高度及坡道的尺寸在这项研究中，科研工作者们使用最小的理论框架将涉及白蚁巢生物构造的三个时空领域联系在一起：构造蚁巢的材料、建造蚁巢的工蚁及标记巢活动区域的分泌信息素。研究者们借此捕获白蚁巢的两个关键的几何和拓扑特征：即每层垂直间距和在相同或相邻层级上的坡道之间的水平间距，以及按月计的筑巢时间。在生物系统中，涉及架构、行为和信息的传递反馈回路驱动了巢的构建。同样，它也与白蚁丘的宏观形态发生有关，并可能为我们理解其它动物结构的出现提供思路——例如蚂蚁或其他白蚁亚科物种的巢穴。在仍然遵循相同基本原理的同时，了解这些系统的相异的复杂构建方式是未来可探索的方向。然而，我们发现白蚁巢结构的关键节点信息会在我们的模型中针对一系列参数值自发出现，这表明它是一个稳健且适应性强的非平衡稳态——也证明伴生菌落植根并响应蚁巢信息。
研究人员希望通过探索由白蚁和其他昆虫建造并居住的建筑，了解它们利用周围环境的能力，从而使我们人类可以更好地了解多种代理系统方法如何提升我们的生活质量——无论使从群体智能还是建筑设计，乃至更广阔的领域。 6.社会科学的黄金时代
期刊来源：PNAS
论文题目：The golden age of social science论文地址：https://www.pnas.org/content/118/5/e2002923118

自奥古斯特·孔德于1842年提出社会学以来，这一领域已经发展了近200年。而随着新数据的获取与新的分析方法的应用，跨学科的研究方法开始融合，这一专业已经进入了新的发展阶段。来自加州理工学院的 Anastasia Buyalskaya 等人就认为社会科学已经进入了黄金时代。但同时他们也对这一领域的发展指出了几项问题。他们的分析于 2021 年 2 月 2 日发表于 PNAS 上。随着新型技术的兴起，越来越多其他专业背景的人士踏足社会科学领域，因此在进行跨学科交流时，论文作者认为需要有一套属于社会科学自己的“普通话”，一套统一的研究框架。此外，论文作者也从社交网络和行为经济学这两个领域对社会科学的发展进行了回顾。最后，作者也呼吁社会科学应当接受“开放科学”的号召，共享程序与数据。并且，专业期刊应当对跨学科论文加以鼓励，而专业的研究团队也应当为吸纳不同背景的研究者指定新的人才方案。 7.大型金融数据中
赌博与财务、社交以及健康之间的关系
期刊来源：Nature Human Behaviour
论文题目：The association between gambling and financial, social and health outcomes in big financial data论文地址：https://www.nature.com/articles/s41562-020-01045-w

对大多数人来说，赌博只是一种普通的消遣，但对另一些人来说却可能导致成瘾以及许多有害后果。2月4日发表在 Nature Human Behaviour 上的一篇文章利用英国一家零售银行提供的匿名数据，在长达7年的时间里，对赌博支出在每月收入中所占比例与31项金融、社交和健康指标之间的相关性进行了研究。
4种指标与赌博支出的相关性举例，更多结果见原文。横坐标为2018年赌博支出占总收入的比重，纵坐标为样本在各个项目上的支出。
研究结果表明，赌博与更大的金融困境和更差的个人金融规划有关，同时也与消极的生活方式、健康状态相关；到达一定阈值后，赌博对死亡贡献的边际效应大幅上升，同时对于赌博习惯的粘性增加。该文章的贡献在于利用金融交易数据，客观量化了赌博对生活其他方面带来不良影响的相关性。在此之前学术界和决策者对赌博的看法占主导地位的流行率调查是自我报告的、横断面的，而且在本质上样本较小。

集智新栏目Complexity Express 上线啦！

Complex World, Simple Rules.复杂世界，简单规则。复杂性科学（Complexity Science）是集智俱乐部多年以来的主题，我们长期追踪关于自然、生命、社会、认知等各类复杂系统的研究进展，并组织学术研讨。同时由于学科交叉融合，大量针对复杂系统的研究成果散落在人工智能、统计物理、网络科学、数据科学、计算社会科学、生命科学、认知科学等等不同领域的期刊会议中，缺乏整合。为了让大家能及时把握复杂系统领域重要的研究进展，我们隆重推出「Complexity Express」服务，汇总复杂系统的最新顶刊论文。 Complexity Express 是什么？
Complexity Express 每天爬取复杂系统领域最新发表的顶刊论文，每周通过“集智斑图”服务号汇总推送。进入 Complexity Express 页面即可随时查看顶刊论文更新，你也可以通过微信接收研究更新推送和一周汇总。

Complexity Express 为谁服务？
如果你是复杂系统领域的研究者，可获得重要论文上线通知，每周获取最新顶刊论文汇总。
如果你是复杂系统领域的学习者，可了解学界关注的前沿问题，把握专业发展脉络。
如果你是传统的生命科学、社会科学等学科中的研究者/学习者，可以从复杂性科学和跨学科研究中获得灵感启发。
如果你是关注前沿研究发现的知识猎手，可获得复杂系统研究对自然和人类世界的最新洞见。Complexity Express 栏目也是集智俱乐部公众号的主要选题来源，诚挚邀请你订阅，与我们信息同步。 Complexity Express 论文从哪里来？
考虑复杂系统研究往往属于跨学科工作，我们主要抓取综合类和泛物理类/计算机类的顶级期刊，从每周新发表的数百篇论文中精选出与复杂系统相关的论文。 Complexity Express 参考影响因子和学者口碑，选择了如下期刊，每日爬取其论文更新：Nature
Science
PNAS
Nature Communications
Science Advances
Physics Reports
Physics Review Letters
Physics Review X
Nature Physics
Nature Human Behaviour
Nature Machine Intelligence
更多期刊持续增补中，欢迎推荐你认为重要的期刊！如果你在 Complexity Express 中发现了感兴趣的论文，请立刻“点赞”！每周最高赞的论文，集智编辑部将组织专业解读~ Complexity Express 追踪哪些领域？
我们力求兼顾热点追踪与领域覆盖，目前筛选的论文主要集中在如下与复杂性关系密切的领域：网络科学各个分支及交叉应用
图数据与图神经网络
计算机建模与仿真
统计物理与复杂系统理论
生态系统、进化、生物物理等
系统生物学与合成生物学
计算神经科学与认知神经科学
计算社会科学与社会经济复杂系统
城市科学
科学学
计算流行病学
以及一些领域小众，但有趣的工作由于复杂性研究领域横跨多个学科，研究论文散落在不同的期刊上，很难不重不漏地把握最新工作。针对复杂性领域的论文筛选，我们专门设计了算法。经过数月的训练迭代优化，目前对上述领域爬取准确率达到90%以上。将来我们还会根据你的具体研究领域，推出研究分类与个性化的订阅服务，敬请期待！由于复杂性领域涉及的论文关键词和研究问题纷繁复杂，所以算法难免有不成熟的地方，如果你发现我们有漏掉的重要论文，或者爬到了领域有偏差的论文，欢迎联系我们（小助手微信：swarmaAI），帮助我们持续优化算法。
如果你对科学学、计算术语学等感兴趣并有代码能力，欢迎报名成为集智算法志愿者/实习生（具体请邮件联系算法组负责人huqiao@swarma.org）。
如果你对复杂性科学及相关跨学科研究有长期兴趣，并乐于解读分享，欢迎加入集智作者团队（具体请邮件联系编辑部负责人liupeiyuan@swarma.org）。