什么是度分布 | 集智百科

“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

本文是对集智百科中“度分布”词条的摘录，参考资料及相关词条请参阅百科词条原文。
本词条由集智俱乐部众包生产，难免存在纰漏和问题，欢迎大家留言反馈或者前往对应的百科词条页面进行修改，一经修改，可以获得对应的积分奖励噢！
本词条由集智俱乐部众包生产，难免存在纰漏和问题，欢迎大家留言反馈或者前往对应的百科词条页面进行修改，一经修改，可以获得对应的积分奖励噢！

一、定义二、观察度分布三、超额度分布四、函数生成方法
五、有向网络的度分布六、符号网络的度分布七、编者推荐八、集智百科词条志愿者招募

在图和网络的研究领域，网络节点的度是它与其他节点的连接数，而度分布 Degree distribution就是整个网络中这些度的概率分布。

定义

网络中一个节点的度（有时会被误认为连通性）是该节点与其他节点的连接或边的数量。如果网络是有向的，里面的边也会具有方向，从一个节点指向另一个节点，那么这些节点就会有两个度，一个度表示入射边的数量，另一个度表示出射边的数量，分别记为入度和出度。

度分布P(k)定义是：网络中度值为k的所有节点与总节点数量的比值，如果一个网络中有n个节点，且其中nk个节点的度值为k，那么 P(k) = nk/n。度分布就是P(k)的整体分布。类似的，对于有向网络也可以定义出度分布和入度分布。

度分布的定义也可以用累积度分布Cumulative Degree Distribution（位置k的累积度分布的值表示网络中度值小于或等于k的概率）的形式来表示，也可以用互补累积度分布Complementary Cumulative Degree Distribution或者逆累积度分布（k处的互补累积度分布的值表示网络中度值大于k的概率）的形式表示，此分布与积累度分布互补。

观察度分布

无论是在研究真实网络（如互联网和社会网络）还是在理论网络，度分布都极为重要。以最简单的网络模型——随机图（ER模型）为例，该网络中的n个节点中任意两个节点之间以概率p连接，以概率p不连接，它们之间为独立事件。整个网络的度服从二项分布，其中度值为k的概率为: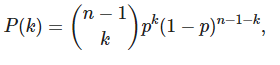

（当n无限大，平均度为<k>=p(n-1)保持有限时，该二项分布可近似为泊松分布）。
但现实世界中的大多数网络的度分布却与上述分布非常不同，它们大多数是高度右偏的，这就意味着网络中的大量节点的度值较低，但少数节点，即所谓的“枢纽”，度值很高。一些网络，尤其是互联网、万维网和一些社交网络，其度分布被认为近似遵循幂律分布 power law:

其中r是一个常数，被称为幂律指数。这种网络被称为无标度网络 Scale-free network，它因其特殊的结构和动力学性质而引起人们的关注。然而，最近有一个基于广泛真实数据的综合性研究认为，如果用严格的统计方法，无标度网络实际上是稀有的。

一些研究人员对这些发现提出了异议，认为研究中使用的定义过于严格，其他人则认为，确定度分布的精确函数形式不必要，只需要知道度分布是否为厚尾分布就好。对度分布的特定形式的过度解释也受到批评，因为它没有考虑网络如何随时间演化。

余度分布

余度分布 Excess Degree Distribution的定义是：沿着任意一条边到达某个节点，这个节点其他边的数量的概率分布。换句话说，它是随链接进入一个节点后出去的边数的分布。
假设一个网络具有度分布P(k),通过选择一个节点（随机或非随机）跟随它的一个邻近点（假设至少有一个邻近点），那么该节点具有k个邻近点的概率不是由P(k)给出的。造成这一结果的原因在于，无论何时在异质网络中选择某个节点，它都更有可能通过跟随该节点的某个现有邻点到达枢纽节点。这些节点具有度k的真实概率是q(k)，它被称为该节点的余度。在配置模型 Configuration Model中，忽略节点之间的相关性，并假定每个节点以相同的概率连接到网络中的其他任何节点，余度分布表示为: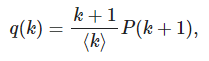
这里<k>是模型的平均度。由此可知，任意节点的邻居的平均度会大于该节点的平均度。推广到在社交网络络中，这意味着你的朋友平均比你拥有更多的朋友。这就是著名的朋友悖论 Friendship Paradox。可以证明，如果一个网络的平均超额度大于1，那么它可以有一个巨大的联通分支: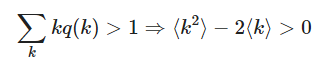

要注意的是，以上两个方程只适用于配置模型，想要准确得到现实世界的网络中的余度分布，还应考虑网络中的度-度相关性。

函数生成方法

生成函数可以用来计算随机网络的不同性质。分别给定某些网络的度分布P(k)和余度分布q(k)，可以以下列形式写出两个幂级数: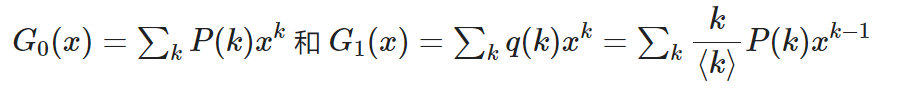

G1(x)的值也可得出通过G0(x)的导数：
‍‍‍‍‍‍

如果已知概率分布P(k)的生成函数，我们可以通过对其微分重新得到P(k)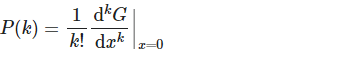

一些性质，如一些矩，然后，可以很容易地进行计算依据G0(x)和它的导数: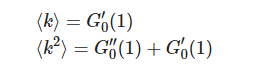

对于服从泊松分布的随机网络，如ER随机图,G1(x)=G0(x)就是这种类型的随机网络理论特别简单的原因。一阶和二阶近邻的概率分布由函数G0(x)和G0(G1(x))生成。进一步扩展，m阶近邻的概率分布由如下式子得到：

G0(G1(….G1(x)….))
其中的G1函数作用到自身（递归调用）m-1次
一阶近邻的平均数量就是 C1 是，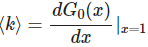

二阶近邻的平均数量是：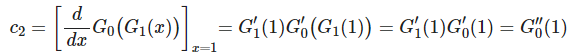

有向网络的度分布

在有向网络中，每个节点都有相应的入度 kin 和出度 kout 分别表示指向该节点的边的数量和从该节点指出的边的数量。若用 P(kin,kout)示随机挑选一个节点，其入度为 kin 出度为 kout 的概率，则对应于这个联合概率分布的生成函数可以写成含有两个变量 x 和 y 的形式：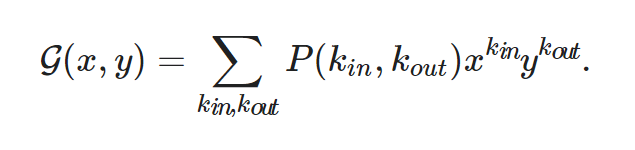

由于有向网络中的每条边必须离开某个节点并进入另一个节点，因此净进入一个节点平均边数是零，即

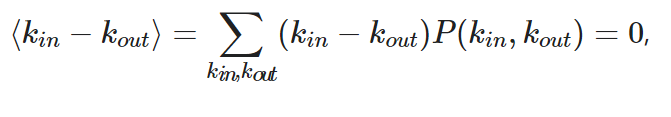这意味着，生成函数必须满足：

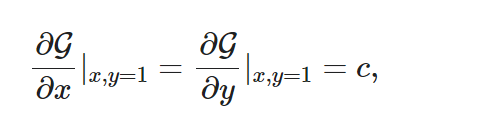
c是网络中节点的平均度（出度和入度）； < kin>=< kout >=c
基于函数g(x,)类似于与前面所述，我们可以得到入/出度分布和入/出的余度分布的生成函数。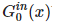可以定义为一个随机选择节点上所到达边数的生成函数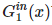，可定义为随机选择的边指向的节点的到达边数的生成函数。我们也可以定义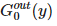和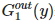表示离开节点的边的数量的生成函数：

这里，一阶近邻的平均数量C1是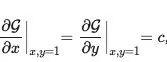
,随机选择一个节点的二阶近邻的平均数量为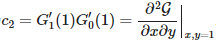。这些也可以分别表示通过指向的边来到某一个节点的一阶近邻和二阶近邻的平均数量，因为这些方程显然是在x和y上对称的。

符号网络的度分布

在符号网络中，每个节点都有一个正度(ｋ+)和一个负度(ｋ-)分别表示连接到该节点的正边和负边的数量。所以符号网络会有正度分布(P(ｋ+))和负度分布(P(ｋ-))

编者推荐

网络动力学课程

集智学园特邀陈关荣、项林英、樊瑛、宣琦、李翔、史定华、李聪、荣智海、周进、王琳等网络科学专家作为导师，依托汪小帆、李翔、陈关荣的经典教材《网络科学导论》，自2月27日起开展系列上线课程，以网络动力学为主线构建网络科学知识体系。欢迎希望进入网络科学领域、提高网络分析能力、与一线专家探讨问题的朋友报名参加！

点击查看课程详情：2021重磅新课：探索网络动力学——网络科学第二期