“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

本文是对集智百科中“重尾分布”词条部分内容的摘录，参考资料及相关词条请参阅百科词条原文。

本词条由集智俱乐部众包生产，难免存在纰漏和问题，欢迎大家留言反馈或者前往对应的百科词条页面进行修改，一经修改，可以获得对应的积分奖励噢！


目录


一、定义
二、常见的重尾分布
三、与胖尾分布的关系
四、重尾密度的估计
五、编者推荐
六、集智百科词条志愿者招募

在概率论中，重尾分布 Heavy-tailed distributions是指其尾部呈现出不受指数限制的概率分布：也就是说，它们的尾部比指数分布 exponential distribution “重”。在许多应用中，关注的是分布的右尾，但是分布的左尾可能也很重，或者两个尾都很重。


重尾分布有三个重要的子类：胖尾分布 Fat-tailed distribution，长尾分布 Long-tailed distribution和次指数分布 Subexponential distributions。实际上，所有常用的重尾分布都属于次指数分布类 subexponential class 。


在使用“重尾” Heavy-tailed一词时仍存在一些歧义。于是就出现了另外两种定义。

有一些作者使用该术语来指代并非所有阶矩都是有限的那些分布，也有一些作者使用这个术语来指代那些没有有限方差的分布。


在这里，给出的是最常用的定义，包括其他定义所涵盖的所有分布，以及具有所有幂矩但通常被认为是重尾分布的对数正态分布 long-normal distributions 。（有时“重尾”用于任何具有比正态分布更重的尾巴的分布。）





定义




重尾分布的定义

如果 X 的矩母函数，Mx(t)对于所有 t>0都是无限的，则具有分布函数 F 的随机变量 的分布被称为重尾（右）。

也可以写成尾分布函数 the tail distribution function ：

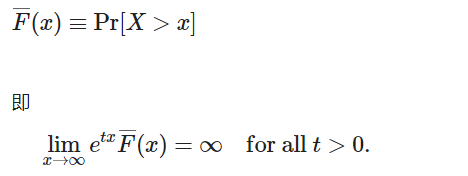
长尾分布的定义

分布函数为 F 的随机变量 X 具有长尾分布，如果对于所有 t>0，都满足

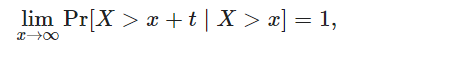
或等价于

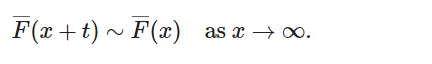
对于右尾长尾分布的随机变量有一个直观的解释，即在长尾分布随机变量尾部取值已超过某个高水平的条件下，它将超过其他更高水平的概率接近于1。


所有长尾分布都是重尾分布，但反过来不一定成立，且可以构造出非长尾分布的重尾分布。

次指数分布

次指数性是根据概率分布的卷积 Convolution 定义的。对于具有共同分布函数 F 的两个独立同分布的随机变量 X1,X2, F与自身的卷积，F*2是二重卷积，使用Lebesgue–Stieltjes积分，方法如下：

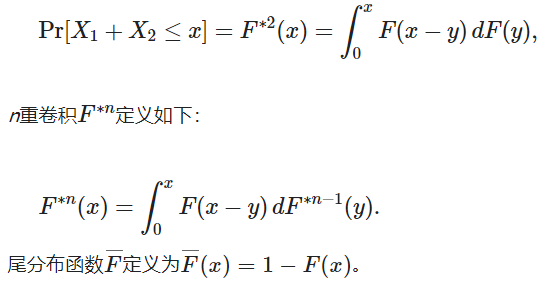
如果满足以下条件，分布 F 在正半轴上是为次指数的

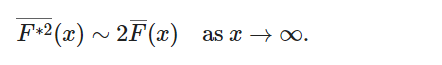
这意味着，对于任何 n>=1，

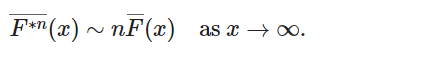
对此的概率解释是，对于具有共同分布 F 的 n 个独立随机变量 X1,….,Xn 的总和

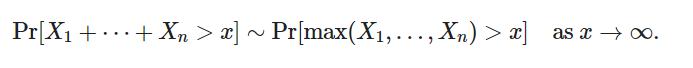
这通常被称为单跳 single big jump或突变理论 catastrophe principle 。


如果分布 FI([0,∞))为实数，则 F为整个实数上的次指数分布。此时 I([0,∞))是正半轴的示性函数。或者，当且仅当 X^+=Max(0，X)是次指数时，则支撑集为实数轴的随机变量 X 是次指数的。


所有次指数分布都是长尾分布，但可以构造出非次指数分布的长尾分布的示例。





常见的重尾分布




所有常用的重尾分布都是次指数的。

单尾的包括：

  • 帕累托分布 Pareto distribution;

  • 对数正态分布 Log-normal distribution;

  • 莱维分布 Lévy distribution;

  • 形状参数大于0但小于1的韦布尔分布 Weibull distribution;

  • 伯尔分布 Burr distribution;

  • 对数逻辑分布 log-logistic distribution;

  • 对数伽玛分布 log-gamma distribution;

  • 弗雷歇分布 Fréchet distribution;

  • 对数柯西分布 log-Cauchy distribution，有时被描述为“超重尾”分布，因为它表现出对数衰减，从而产生比帕累托分布更重的尾。

双尾的包括：

  • 柯西分布 Cauchy distribution本身就是稳定分布和t分布的特例；

  • 稳定分布族 The family of stable distributions，但该族中正态分布的特殊情况除外。一些稳定的分布是单面的（或以是半轴为支持），例如莱维分布。另请参见具有长尾分布和波动性聚类的财务模型。

  • t分布

  • 偏对数正态级联分布 The skew lognormal cascade distribution。





与胖尾分布的关系




胖尾分布是指对于较大的 x ，以幂律的速度 x^-a趋向于0。由于这样的幂总是受到指数分布概率密度函数的限制，因此，胖尾分布始终是重尾分布。


但是，某些分布的尾部趋近于零的速率比指数函数慢（表示它们是重尾），而比幂快（表示它们不是胖尾）。例如对数正态分布。当然，许多其他的重尾分布，例如对数逻辑分布和帕累托分布也属于胖尾分布。





重尾密度的估计




Markovich中给出了估计重尾和超重尾概率密度函数的非参数方法。

这些是基于可变带宽 variable bandwidth和长尾核估计 long-tailed kernel estimators的方法。将初步数据以有限或无限间隔变换为新的随机变量，这样更便于估计，然后对获得的密度估计进行逆变换；以及“拼合方法”，它为密度的尾部提供了确定的参数模型，并为近似密度模型提供了非参数模型。非参数估计器需要适当选择调整（平滑）参数，例如核估计的带宽和直方图的组距。这种选择众所周知的数据驱动方法是基于最小均方误差及它的渐近性和上界的交叉验证及修改方法。

可以找到一种差异方法，通过使用众所周知的非参数统计量（例如Kolmogorov-Smirnov’s，von Mises和Anderson-Darling的统计量）作为分布函数（dfs）空间中的度量，并将后来的统计量的分位数作为已知的不确定性或差异值。自助法 Bootstrap是另一种工具，可以通过不同的重抽样方案使用未知MSE的近似值来查找平滑参数。




编者推荐



课程推荐

巴拉巴西网络科学

本课程中，我们有幸邀请了汪小帆、赵海兴、许小可、史定华、陈清华、张江、狄增如、陈关荣、樊瑛、刘宗华这十个来自六大不同高校、在网络科学领域耕耘许久的教授作为导师，依据教材框架，各有侧重地为我们共同勾勒出整个学科的美丽图景，展示这个学科的迷人魅力，指引这个学科的灿烂未来。

巴拉巴西网络科学

课程推荐：巴拉巴西网络科学 

https://campus.swarma.org/course/1754


复杂网络2020

本课程是由北京师范大学樊瑛老师所筹划的课程，这个课程对复杂性科学的一个概述，包含10个章节，每节都会涵盖复杂系统的一个主要概念。

课程推荐： 圣塔菲课程: Introdution to Complexity

https://campus.swarma.org/course/1349


厚尾分布

本课程是由北京师范大学陈清华老师所筹划的课程，这个课程结合实际数据和丰富的学术文献，从各方面向大家展示幂律分布——复杂系统入门必修课，其特征和意义，以及如何应用，为大家打造了体系完整的幂律分布学习框架！

课程推荐： 复杂系统中的幂律分布（首节免费）

https://campus.swarma.org/course/647


路径推荐

  • 解读幂律(Power Law)分布与无标度(Scale Free)网络

https://pattern.swarma.org/path?id=21

本文节选自陈清华老师的线上讲座《解读幂律与 无标度网络 ——贫穷限制了我们的想象力》。详细的介绍了：

  • 什么是幂律分布

  • 什么是无标度网络

  • 如何产生幂律分布

  • 如何估计和判断幂律分布





百科项目志愿者招募




作为集智百科项目团队的成员，本文内容由Jie，Smile，思无涯咿呀咿呀，丁义明老师参与贡献。我们也为每位作者和志愿者准备了专属简介和个人集智百科主页，更多信息可以访问其集智百科个人主页。


以上内容都是我们做这项目的起点，作为来自不同学科和领域的志愿者，我们建立起一个有效的百科团队，分配有审校、翻译、编辑、宣传等工作。我们秉持：知识从我而来，问题到我为止的信念，认真负责编撰每一个词条。




在这里从复杂性知识出发与伙伴同行，同时我们希望有更多志愿者加入这个团队，使百科词条内容得到扩充，并为每位志愿者提供相应奖励与资源，建立个人主页与贡献记录，使其能够继续探索复杂世界。


如果你有意参与更加系统精细的分工，扫描二维码填写报名表，我们期待你的加入！



集智百科报名表


来源：集智百科

编辑：王建萍



推荐阅读


点击“阅读原文”，阅读重尾分布词条原文与参考文献