网络嵌入是复杂网络分析的重要手段，而网络嵌入维度的选择，对嵌入算法的性能优劣有着至关重要的影响。6月18日最新发表于Nature Communications的论文，从网络几何学的分析视角，提出了一种自动判定网络最优嵌入维度的算法，该算法能够在不依赖下游机器学习准确率的前提下，自动判定出不同嵌入算法的最优维度。论文第一作者谷伟伟任教于北京化工大学信息学院，是集智科学家社区成员。
研究领域：深度学习，网络表征学习，复杂网络几何学
论文题目：
Principled approach to the selection of the embedding dimension of networks
论文网址：
https://www.nature.com/articles/s41467-021-23795-5
对于复杂网络中的节点，其结构信息，可以通过神经嵌入（Neural embedding）用低维、稠密的向量空间表示高维、稀疏的网络结构，用低维度向量来表征网络中的结构模式。所学习到的嵌入向量可用于节点分类、链路预测、社团划分等机器学习任务。使用经过嵌入后的数据作为算法输入，可以提升预测性能。
区别于双曲嵌入等具有明晰含义的嵌入算法，基于神经网络的嵌入算法采用实值向量表征节点，将网络的嵌入维度一般作为一个超级参数，通常依据行业经验设置为100到300之间的数值。或者依据下游具体机器学习任务的表现，来选择最优维度。鲜有研究探究网络结构对嵌入维度的影响。网络的大小及结构各异，很难找到一个普遍使用的经验值，例如自然界的道路交通网络的嵌入维度可以近似为二维，而节点之间彼此紧密连接的网络趋于同质性，可以近似为一维。
于是，将网络转换为一个多少维度的嵌入，大多依照经验。在自然语言中，可以通过经验设定嵌入维度，但网络的大小和结构各异，很难找到一个普遍使用的经验值。另一种方式，是根据具体任务表现在不同的嵌入维度下，何时最优进行判定，选择那个能够让判断任务表现最佳的嵌入维度。
于该文相关的研究，一是以相近的基于几何的方法，分析自然语言中的词嵌入[1]，找出词向量对的最优维度，另一个是对社交网络嵌入中的不确定性进行定量评估及可视化的[2]。而从信息论的视角，审视自然语言处理中的词嵌入的最优维度的，是[3]。
在真实场景下，随着网络规模的增长，预期能够表征网络中大部分结构信息的嵌入维度也会增长。如何找到不同尺度的网络所对应的最小嵌入维度，是该研究要解决的核心问题。通过采用成对内积（Pairwise Inner Product PIP），该研究提出一个确定一个适合嵌入维数值的方法，指出最优的嵌入维度，处于偏差（variance）和误差（bias）的最优平衡处，而嵌入维度升高与对应的结构信息呈幂律分布。
该文通过定义任意节点之间的几何距离并计算任意嵌入维度与最优嵌入维度之间差值的方式，在不同网络，不同嵌入算法中发现了网络嵌入误差的下降曲线与链路预测、社团划分、节点分类的准确率上升曲线具有良好的对应关系。网络嵌入的误差随嵌入维度的分布服从幂率分布。
首先将嵌入维度无限时的信息损失，看成是最优嵌入，通过对比降维到d时的损失情况与其的差距，可以评估当前维度下的相对信息损失，将其设为L(d)，可以通过下式，对其拟合，其中s 和 α 待优化参数。
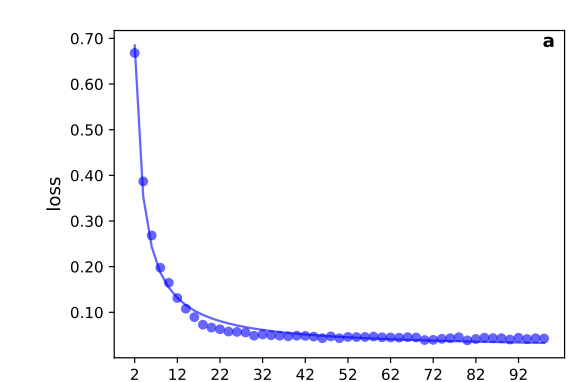
为了评估不同嵌入维度造成的信息损失，通过对包含135个节点的美国大学橄榄球网络，使用node2vec和LINE两种嵌入方法，判断随着网络嵌入维度的增加，其标准化后的嵌入损失函数（normalized embedding loss function）的变化情况，如下图a所示。其中蓝色点对应的node2vec算法和理论预期的结果一致，而LINE算法和理论预期的差异，指出了算法特异性的影响。注意node2vec算法在维度更低时，损失函数的下降更快，但这不意味着该算法能够更好的表征网络信息，因为信息损失的定义是和具体算法相关的，其下降速度的对比不能指示嵌入算法的好坏。
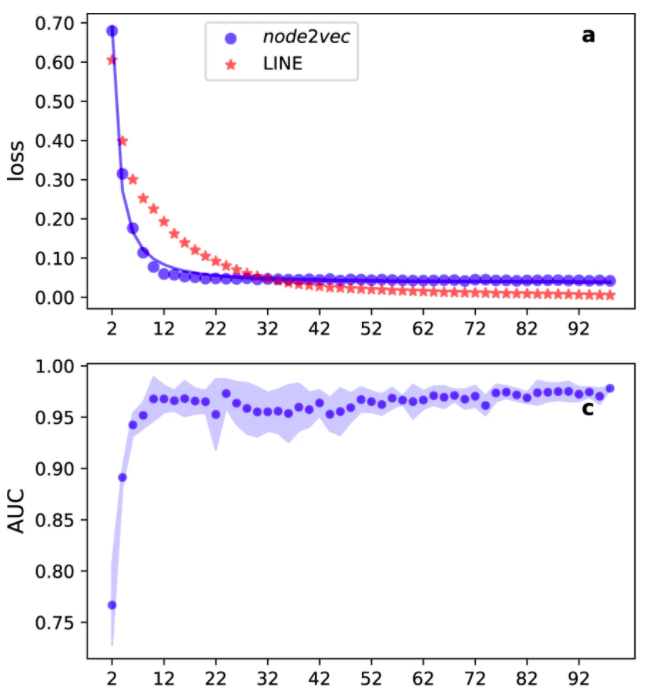
图1. a,American college football网络使用不同的嵌入维度，其信息损失的下降曲线;c,基于node2vec算法不同维度的嵌入进行链路预测时的准确度评估曲线
而对Cora引文网络进行网络嵌入时，发现了相同的趋势。考虑到LINE是针对大规模网络嵌入优化过的算法，其能够在相同的维度下，更显著的降低信息损失。
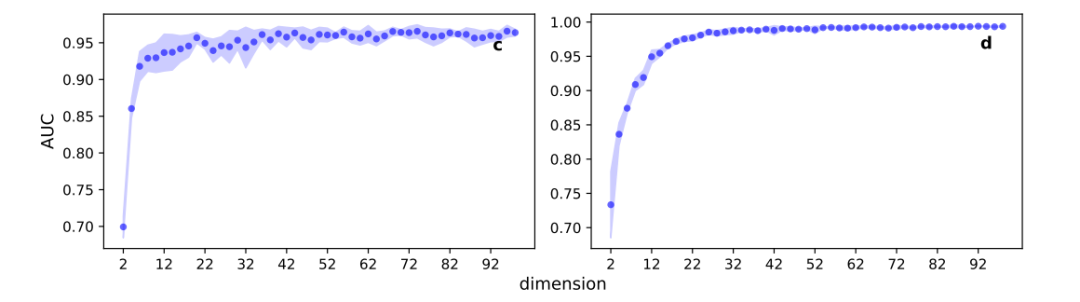图2. 上述的两种网络中，基于不同维度的嵌入进行链路预测时的准确度评估曲线
链路预测任务中，American college football使用10维或者更小的维度，就能够以较好的准确度进行预测，而在这个维度，甚至在此之前，相对损失函数就开始饱和，这意味着链路预测任务并没有用到全部网络嵌入所编码的结构信息。
当我们对模拟网络，进行几何嵌入（geometric embedding ）时，也能发现类似的规律，即预估的损失和实际基本一致，且该曲线能够对应（提前指示）预测任务上的性能饱和（saturation）点。
图3. 在模拟的随机块（stochastic block）模型中，嵌入维度和信息损失的散点图呈现类似的规律
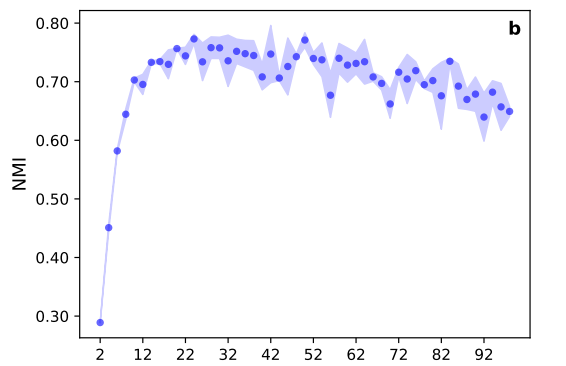
图4. 社群检测（community detection）算法在不同维度的嵌入下的平均表现情况，其中表现最优的维度，同样出现在信息损失函数呈现饱和值之前
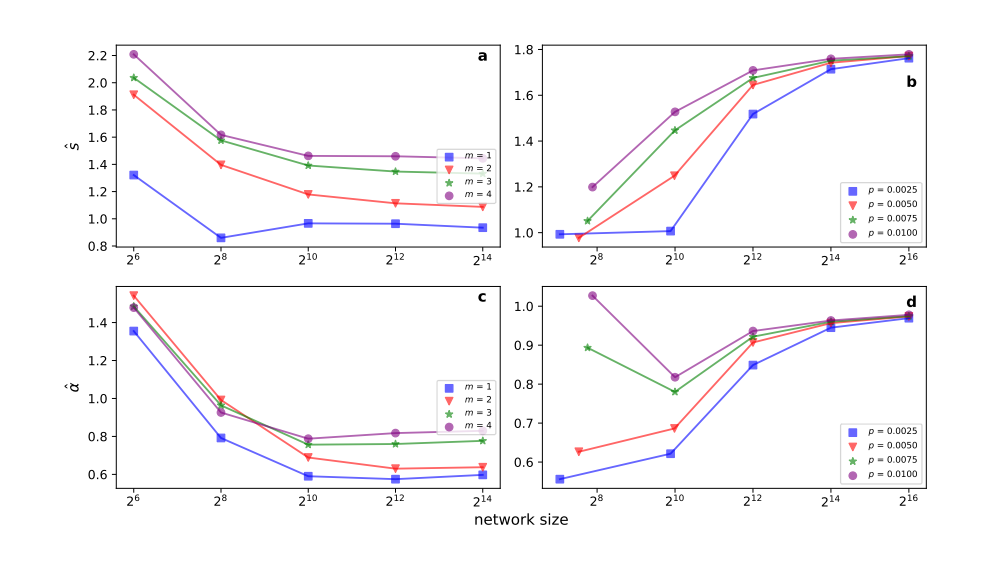
在BA模型的模拟数据中，不同大小和节点密度的网络，其对应的参数如下所示，该图说明了该算法在不同类型的网络下的参数稳定性。
图5. BA模拟网络大小和密度和最优嵌入维度参数的对应关系
而在运行多次嵌入算法，通过不同运行结果的方差（又称为embedding coherence），来评价嵌入算法随机性的影响时，会发现其结果相对稳定，尤其是在较高的嵌入维度时。
图6. 使用不同维度的嵌入时，American college football网络和Cora引文网络的embedding coherence 随嵌入维度的变化散点图
Embedding coherence 随嵌入维度增加单调下降，这结合之前发现的网络中链路预测，图聚类任务所需的维度，低于最优嵌入维度，可解释为何使用比最优维度高的维度进行嵌入时，预测效果不会变差。
以上实验，综合起来论证了该方法找出的最优维度是可靠的。
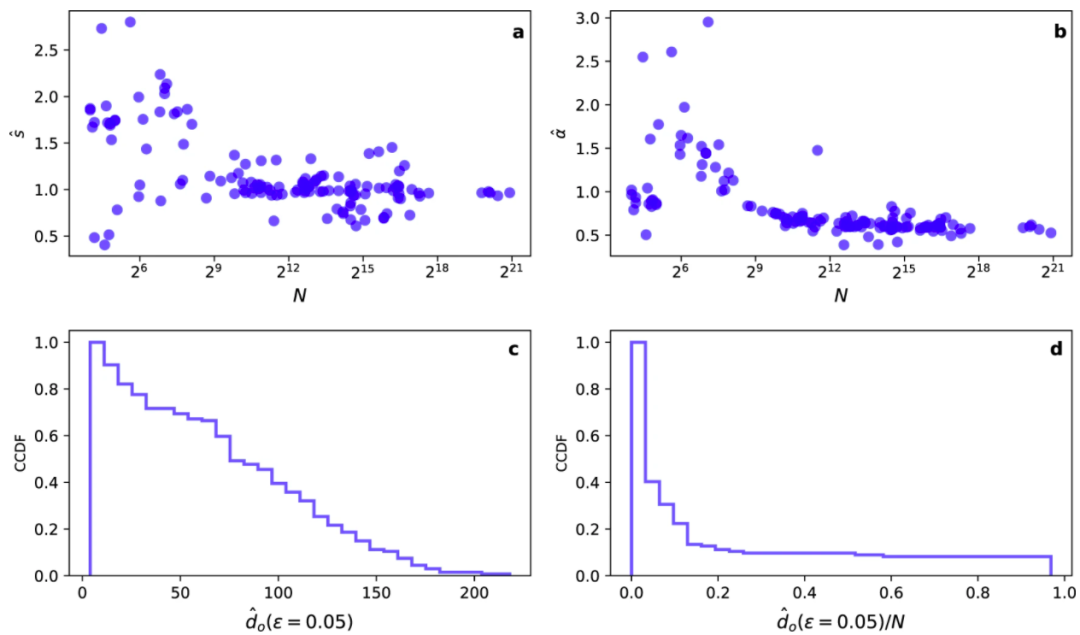
大型网络的实验结果（研究的普遍性）以上实验，论证了该方法找出的最优维度是可靠的，而将该方法应用于135个真实世界中的网络，该研究发现大多数情况下，预估的最优维度远远小于实际网络中的节点数，虽然该方法并不能排除存在一个对这些网络更优的表征方法，能够以更低的维度无损地表征网络中的结构信息，但该研究指出了可表征网络结构信息的维度通常偏低。
图7. 图a和图b135个真实网络下的模型2个参数分布图，图c，真实网络的最优嵌入维度的累积密度分布，其中大部分的最优维度都小于20
总结来看，该研究原创性的从几何视角审视网络嵌入，找出了一种通用的评价网络内在维度的方法，其结果和谱聚类预测的理论值相近。作者发现大部分真实的网络，都可以用远小于其节点数的维度表示。通过该方法预测的最优嵌入维度，能够指出在下游分析中，何时会表现得更好，从而减少了试错成本。
[1] On the Dimensionality of Word Embedding
[2] Latent Space Approaches to Social Network Analysis
[3] Word2vec Skip-gram Dimensionality Selection via Sequential Normalized Maximum Likelihood
集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：
点击“阅读原文”，追踪复杂科学顶刊论文
