PNAS前沿：几何分叉增长模型再现复杂网络演化过程

导语

揭示复杂网络的增长演化机制为人们理解复杂网络的动态特性、结构特征以及系统的功能具有重要的作用。如何从有限的观测数据中预测复杂网络的演化趋势一直是网络科学的难题。今年5月底发表在 PNAS 的一项工作提出了双曲空间下的几何分支增长模型，利用有限的网络快照，预测了100多年科学引文网络和世界贸易网络的自相似演化过程，再现了复杂网络的谱系。同时，结合之前的几何重整化模型，该工作成功实现了网络由大到小和由小到大的自由变换，建立了一套完整的复杂网络自相似变换方法。该成果还可以应用到检测最优网络大小以最大程度地响应外部驱动，有限尺度效应下的相变和临界行为分析等等。

研究领域：复杂网络演化，双曲网络模型，网络自相似变换

郑木华 | 作者

邓一雪 | 编辑

论文题目：

Scaling up real networks by geometric branching growth

论文链接：

https://www.pnas.org/content/118/21/e2018994118.short

1. 真实网络的自相似演化

从现实社会的关系网到虚拟的互联网，从线下到线上，我们的生活始终没有脱离复杂网络。真实的复杂网络从其诞生就不断地演化着。网络节点不断地增加，节点之间的连接在不断地增长。然而，复杂网络的形成机制是什么？具有什么样的演化规律？它的演化机制对网络的功能和动力学行为有什么影响？为了回答这些问题，科学家们对复杂网络增长演化机理的探索从未停止。在以往的研究中，人们常常认为系统的增长演化机制是新生节点依次诞生并逐渐加入到原网络中。然而，在许多真实系统中，网络的增长模式并非如此。它们是通过分叉进化的方式来增长的，例如学科划分、国家分裂以及物种进化等等。这样的增长方式对网络结构和功能有什么影响？对此，我们知之甚少。缺乏充分的实证数据支持，探索系统分叉增长规律的研究一直很难展开。如何从有限的观测数据中构建模型，理解网络增长演化规律，预测其发展趋势已成为网络科学中面临的一大难题。

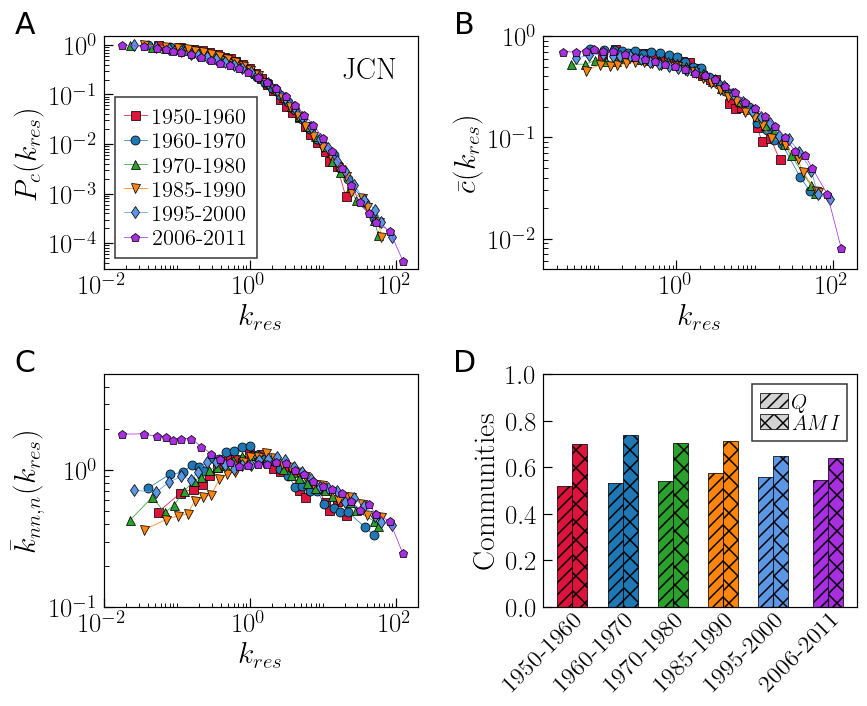
图1. 复杂网络的自相似演化。A-C分别呈现了不同时间快照下，科学引文网络（JCN）中的度分布、聚类系数谱和度度关联。D给出了相应快照下的社团结构情况。

最近，来自江苏大学的郑木华博士及其合作的研究团队在《美国科学院院刊》(Proceedings of the National Academy of Sciences，PNAS) 发表了一篇利用几何分叉增长模型来放大真实网络的论文，突破了以上难题。他们分析了100多年科学引文网络（journal citation network，JCN）和世界贸易网络（world trade web，WTW）的数据，发现了真实系统在增长演化的过程中具有自相似性——他们分析了不同时间快照下网络的度分布、聚类系数谱、度度关联、社团结构等统计特性，发现对以这些网络统计指标作平均度变换时，它们的标度几乎不变（图1中的线几乎重叠）。值得注意的是，这些系统在演化过程中是加速增长的：网络节点数增加，网络平均度也随时间增加的。然而，为什么这些系统在加速增长演化的过程中还能保持自相似行为？文中对此展开了研究。

2. 几何分叉增长模型与几何重整化模型

为了更好地理解真实系统增长演化过程中的自相似性行为，研究者等人认为，构建具有自相似特性的复杂网络演化模型是关键。此时，研究者及其合作者们联想到了之前他们几何重整化网络的工作[1-2]：通过几何重整化变换的方法，一层一层地缩小原网络，缩小的网络和原始网络在结构上高度一致，具有很好的自相似性特征。网络演化的过程和将低分辨率小网络放大的逆重整化过程一致。如果能实现高效的复杂网络逆重整化，那么理解复杂系统的自相似行为将变得简单。然而，如何对复杂网络进行逆重整化变换一直是统计物理和网络科学面临的科学难题。由于网络由低维向高维生长过程中复杂性快速增加，再加上新节点、新连边、噪声等不确定性因素的影响，网络逆重整化变换过程中很容易丢失原始网络的结构特征（自相似性丢失）。在此工作中，研究者等人从网络双曲空间的角度提出了一个全新的几何分叉增长模型（也是网络逆重整化模型）。基于几何重整化网络的思想，他们将祖先（ancestor）节点分叉生成后代（descendant）节点，通过保持节点双曲空间的位置和连边概率与原始网络的一致性，该模型很好地解决了网络增长过程中自相似性丢失的问题（如图2所示）。不仅如此，结合之前的网络重整化方法，他们成功实现了网络由大到小和由小到大的自由变换，建立了一套完整的复杂网络自相似变换方法。

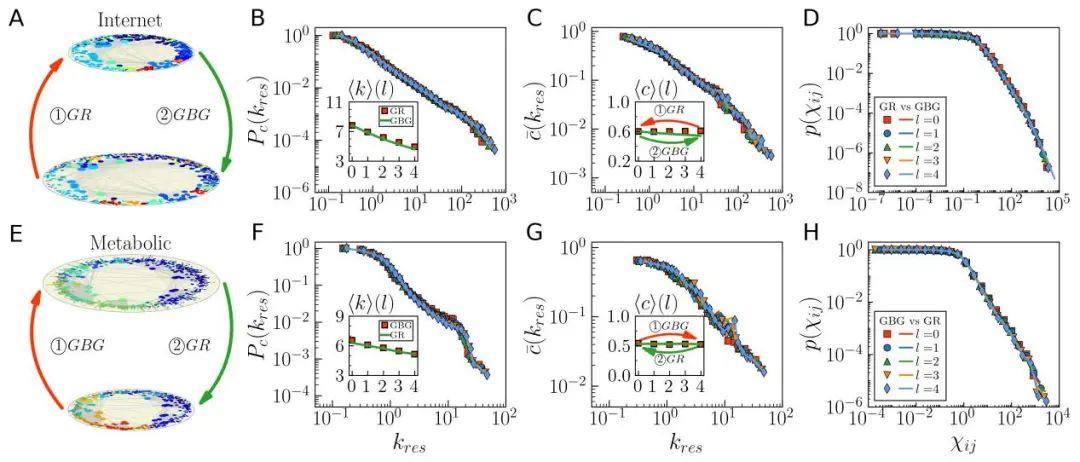
图2. 复杂网络几何重整化和逆重整化变换。A 给出了用几何重整化方法将Internet网络缩小，再用几何逆重整化方法进行还原的示意图。B-D分别呈现了两种变换方法下的网络度分布、聚类系数谱和连接概率的对比图。B和C的插图给出了网络平均平均度和平均聚类系数的对比情况。E-H给出了先用逆重整化方法放大Metabolic网络，再用几何重整化方法还原网络的结果。

3. 几何分叉增长模型

预测复杂网络的自相似性演化

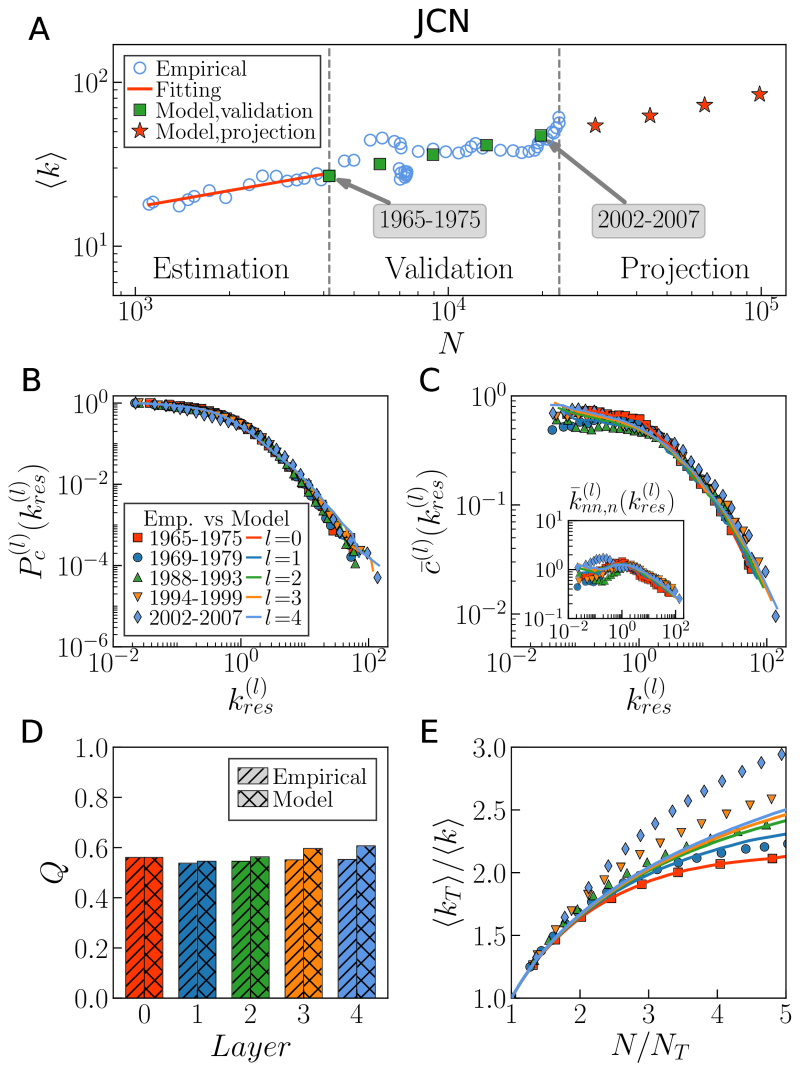
图3. 几何分叉增长模型预测复杂网络的自相似性演化。A平均度随网络规模的变化情况，两条竖直虚线将数据划分成参数估计、模型检验、预测三部分。B-E给出了模型和真实数据相互检验的结果。

在发现了几何分叉增长模型与几何重整化模型的等价性之后，研究者等人试图利用几何分叉增长模型预测网络的自相似性演化。在100多年的科学引文网络和世界贸易网络的数据中，研究者等人发现网络平均度随着网络规模指数增长（如图3A所示）。这种特性为估计几何分叉增长模型的参数提供了可能。如图3A所示，他们将数据按时间窗口分成3部分，少数的观测数据用于参数估计，一部分用于检验模型的有效性，最后一部分用于预测未来的发展趋势。图3 B-E 检验了模型和真实数据的比对结果。从中可以看出，从有限的观测数据出发，几何分叉增长模型可以重新创建复杂网络的谱系（the family tree of complex networks），高效地预测复杂网络结构的增长演化趋势。

4. 更多实际应用

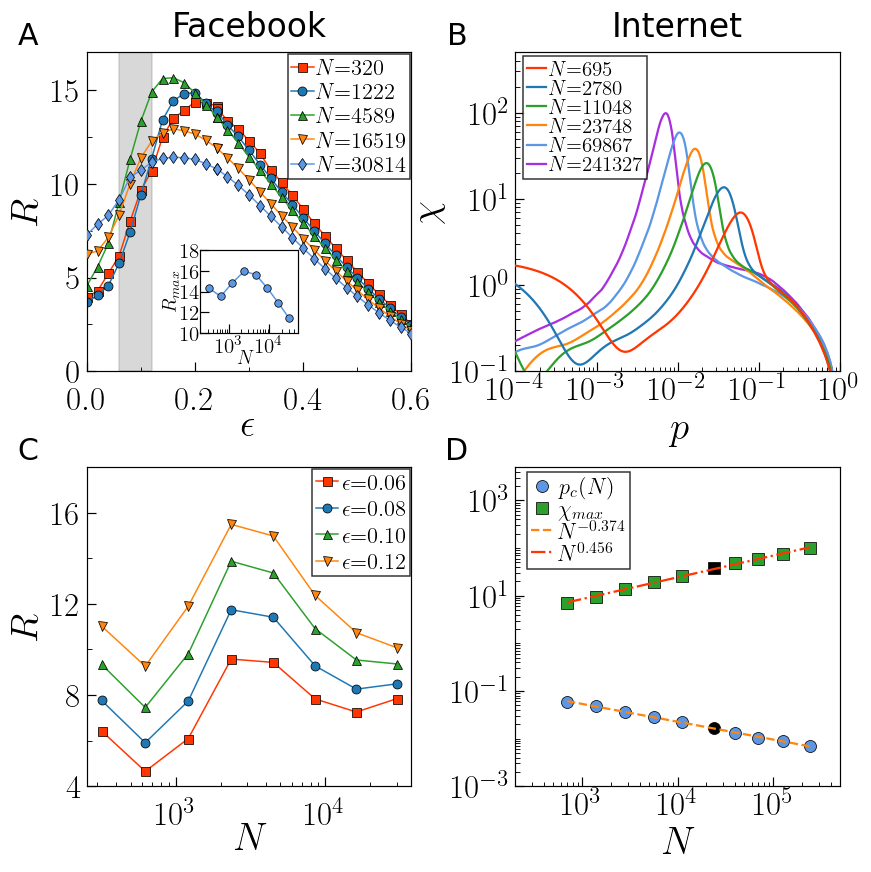
图4 复杂网络自相似变换的应用。A和C检测最优网络大小以最大程度地响应外部驱动。B和D有限尺度效应下的相变和临界行为分析。

最后，研究者及其合作者们还给出了几何分叉增长模型更多的实际应用。他们发现，几何分叉增长模型可以将一个低分辨率的小网络生成一系列与原始小网络高度吻合的高分辨率大网络；而几何重整化模型又可以将一个高分辨率的大网络高效地缩小。如果只有一个网络快照，结合这两个模型，他们就可以变换出不同大小尺度的网络，进而分析不同网络尺度下的动力学行为。如图4所示，他们在文中给出了两个例子：（1）只用一个观察的网络快照，他们就可以检测到最优的网络大小以最大程度地响应外部驱动。（2）从一个实际网络出发，他们可以分析有限尺度效应下的相变和临界行为。

5. 结语

复杂网络自相似变换的研究具有重要的意义：一方面，将大规模网络缩小（重整化）可以降低复杂性，方便结构和动力学分析；另一方面，将低分辨率的小网络放大（逆重整化）可以获得高分辨率图像，有利于分析尺度效应对动力学行为的影响。这个工作实现网络由大到小和由小到大的自相似变换，解决了复杂网络重整化和逆重整化自由变换难题，成功预测了科学引文网络和世界贸易网络的自相似演化过程，极大地推动了网络科学的发展，为人们理解复杂系统的结构和功能具有重要的意义。

参考文献

1. García-Pérez, G., Boguñá, M., & Serrano, M. Á. Multiscale unfolding of real networks by geometric renormalization. Nature Physics, 14(6), 583-589 (2018).

2. Zheng, M., Allard, A., Hagmann, P., Alemán-Gómez, Y., & Serrano, M. Á. Geometric renormalization unravels self-similarity of the multiscale human connectome. Proceedings of the National Academy of Sciences, 117(33), 20244-20253 (2020).

复杂科学最新论文

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：