几十年来,数学家一直希望证明在在物理系统从一种状态转变为另一种状态时,对称性是普遍存在的。被称为共形不变性(conformal invariance)的对称性,实际上包含三个独立的对称性:旋转对称性、平移对称性和标度不变性。近期,一些数学家证明,在临界时刻,被称为旋转不变性的对称性是许多物理系统的普遍属性。
研究领域:相变,对称性,伊辛模型,渗流模型
潘佳栋 | 作者
刘培源 | 审校
邓一雪 | 编辑
50多年来,数学家一直在寻找一种严谨的方法来证明对称性在物理系统从一种状态转变为另一种状态时是普遍存在的。被称为共形不变性(conformal invariance)的对称性,实际上包含三个独立的对称性。
现在,在2020年12月发布的证明[1]中,一个由五名数学家组成的团队更接近证明出共形不变性是物理系统在相变时的必要特征。这项工作确定了旋转不变性(共形不变性中三个对称性之一)存在于各种物理系统的相变边缘上。
以色列魏茨曼科学研究所的加迪·科兹马(Gady Kozma)[2]说:“这是一项重大贡献,它已经发布了很长时间。”
图1:通过多孔介质的渗流模型,与最近关于相变对称性的重要工作有关。
旋转不变性是圆表现出的对称性。将圆旋转任意度数,它看起来都一样。这意味着在处于相变边缘的物理系统中,无论系统模型如何旋转,系统都可以表现出一些相同的属性。
早期的结果已经证明旋转不变性适用于两个特定模型,但他们的方法不够灵活,无法应用于其他模型。 新的证明标志着旋转不变性是一系列模型中的普遍现象。
法国高等科学研究所 (IHES) 和日内瓦大学的雨果·杜米尼尔·科平(Hugo Duminil-Copin)[3]说:“这种普遍性结果更加有趣”,因为这意味着无论物理系统模型之间有什么差异,都会出现相同的现象。
杜米尼尔·科平与里昂高等师范学院的卡罗尔·卡杰坦·科兹洛夫斯基(Karol Kajetan Kozlowski)[4]、日内瓦大学的德米特里·克拉春(Dmitry Krachun)、弗里堡大学的伊昂·马诺莱斯库(Ioan Manolescu)[5]以及IHES和巴黎萨克雷大学的Mendes Oulamara[6]是这项工作的合作者。
这项新工作带来了新的希望,数学家们可能正在接近一个更加宏大的结果:这些物理模型是共形不变的。 在过去的几十年里,数学家已经证明了共形不变性适用于一些特定的模型,但他们一直无法证明它适用于所有模型。这个新的证明为获得全面的结果奠定了基础。
日内瓦大学的斯坦尼斯拉夫·斯米尔诺夫(Stanislav Smirnov)[7]说:“这是一个非常大的突破,共形不变性现在看起来触手可及。”
一种状态和另一种状态之间的转换是自然界中一些最令人着迷的事件。 有些是突然的,比如水加热成蒸汽或冷却成冰时的转变。其他的,比如在新工作中研究的相变,它在两种状态之间有一个模糊的边界。正是在这些临界点,系统处在过渡状态。
举个例子,当你加热铁时,当它超过一定温度,它会失去磁性。这种变化发生在数以百万计的原子作为微型磁铁翻转并且不再与它们邻居的磁性位置对齐时。大约1000华氏度,热效应获得胜利,磁铁就变成了一块金属。
数学家用伊辛模型[8]研究这个过程。它将一个铁块想象成一个二维方形格子,很像一张方格纸上的网格。 该模型将铁原子置于晶格线的交点处,并将它们表示为向上或向下的箭头。
伊辛模型在1950年代被广泛用作表示临界点附近物理系统的工具。这包括失去磁性的金属、空气中的汽液转变和金属有序和无序之间的转换。这些都是不同类型的系统,它们在微观层面上以不同的方式运行。
然后,在1970年,年轻的物理学家亚历山大·波利亚科夫( Alexander Polyakov)[9]预测[10],尽管这些系统存在明显差异,但这些系统在其临界点都表现出共形不变性。经过数十年的分析,物理学家相信波利亚科夫是对的,但是数学家们面对着严格证明的艰巨工作。
共形不变性由三种类型的对称性组成,它们共同组成一种更广泛的对称性。研究人员可以移动物体(平移对称),将它们旋转任意度数(旋转对称),或更改它们的大小(标度对称),所有这些都不会改变它们的任何角度。
杜米尼尔·科平(Duminil-Copin)说:“对于共形不变性,有时我称之为‘统治对称性的对称性’,这是因为它是一种整体对称性,比其他三种对称性更强。”
共形不变性以更微妙的方式出现在物理模型中。在伊辛模型中,当磁性仍然完整且尚未发生相变时,大多数箭头的指向可以形成巨大的原子团。 还有一些小原子团,其中所有箭头都指向下方。但是在临界温度下,原子可以以更远的距离相互影响。在临界点,各处的原子排列都变得不稳定:大小不一、箭头朝上或朝下的原子团同时出现,磁性临近消失。
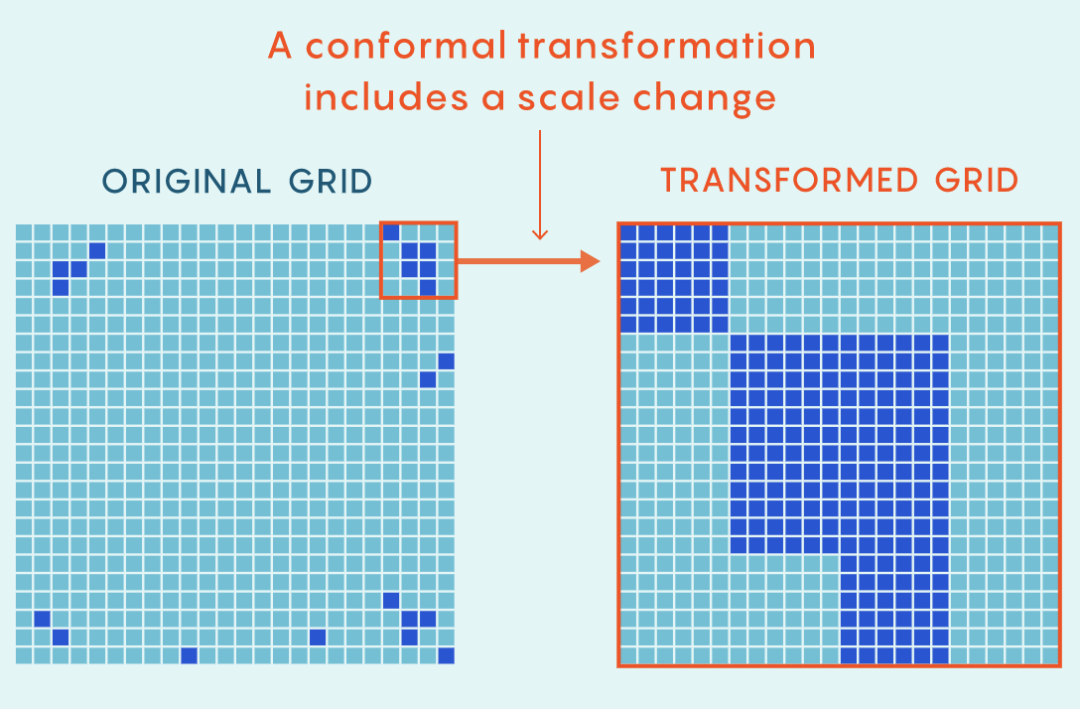
图2:系统发生相变前和发生相变后。图中不同的颜色表示不同的磁场方向。大多数原子排列按磁场方向对齐,并且此时格点并非共形不变的:发生相变前和发生相变后的具有相同磁场方向的原子团的大小不同。
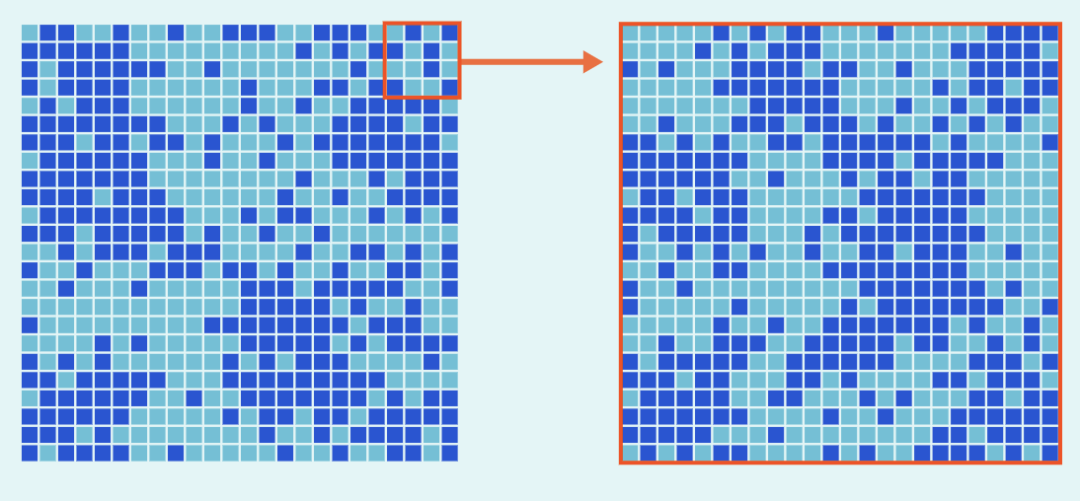
图3:系统发生相变过程中。原子迅速改变它的磁场方向,网格具有共形不变性:前面和后面的具有相同磁场方向的原子团大小相同。
在这个临界点,数学家观察模型并研究箭头之间的相关性,这表示了给定一对格点指向同一方向的可能性。在此设置中,共形不变性意味着可以平移、旋转和缩放网格,而不会改变这些相关性。也就是说,如果两个箭头有50%的机会指向同一方向,然后使用这些对称性,那么在晶格中占据相同位置的箭头也有50%的机会对齐。
结果是,如果将原始晶格模型与变换后晶格模型进行比较,将无法分辨原来的和新的模型。重要的是,相变之前的伊辛模型并不是这样的。在那里,如果将格子的顶角调整为与原始大小相同的大小,这将增加向下箭头原子团的大小,从而很明显得到哪个格子是原来的。
共形不变性具有直接的物理意义:它表明即使调整物质的微观细节,系统的全局行为也不会改变。 它还暗示了某种优雅的数学,就像整个系统正在打破其总体形式并成为其他东西一样。
2001 年,斯米尔诺夫提出了物理模型中共形不变性的第一个严格数学证明[11]。 它适用于渗流模型,即液体在多孔介质(如石头)中穿过的过程。
斯米尔诺夫研究了三角形格子上的渗透,其中水只能流过“开放”的顶点。最初,每个顶点对水流开放的概率相同。 当概率较低时,水流穿过石头的可能性较低。
但是随着研究人员慢慢增加概率,会出现一个点,有足够多的顶点打开以创建穿越石头的第一条路径。斯米尔诺夫证明,在临界点处,三角形晶格是共形不变的,这意味着无论如何使用共形对称对其进行变换,都会发生渗流。
五年后,斯米尔诺夫在2006年的国际数学家大会上宣布他证明了共形不变性[12],这一次是在伊辛模型中。结合他2001年的证明,这项工作为他赢得了数学界的最高荣誉“菲尔兹奖”。
从那以后的几年里,研究人员提出了一些其他证明,为一些特定模型建立了共形不变性,但是没有人能够证明波利亚科夫所设想的共形不变性的普遍性。
纽约大学阿布扎比分校的数学物理学家费德里科·卡米亚(Federico Camia)[13]说:“之前的证明是针对特定模型的。你需要有一个非常具体的工具来证明一个非常具体的模型。”
斯米尔诺夫本人承认,他的两个证明都依赖于他使用的两个模型中存在但通常不可用的某种“魔法”。他说,“这项新工作是第一个打破这种模式的工作——它证明了旋转不变性,这是共形不变性的核心特征,在物理模型中广泛存在。”
杜米尼尔·科平在2000年代后期首次开始考虑证明共形不变性的普遍性,他当时还是斯米尔诺夫在日内瓦大学的研究生。 他对导师证明的辉煌以及他们的局限性有着独特的理解。 斯米尔诺夫绕过了分别证明所有三个对称性的需要,而是找到了建立共形不变性的直接途径——就像通往山顶的捷径一样。
“他是一个了不起的问题解决者。 他在这座巨大的山上找到入口,证明了两种统计物理学模型的共形不变性,就像他经过难点一样。”杜米尼尔·科平说。
在研究生毕业后的几年里,杜米尼尔·科平致力于提出新的证明。当他和他的合作者开始认真研究共形不变性时,他们已经准备好采用与斯米尔诺夫不同的方法。他们没有用魔法冒险,而是回到了波利亚科夫和后来的物理学家提出的共形不变性的最初假设。
图4:法国高等科学研究所和日内瓦大学的杜米尼尔·科平和他的合作者正在采用一次一个对称的方法来证明共形不变性的普遍性。
物理学家需要分三个步骤进行证明,共性不变性都存在对称性:平移不变性、旋转不变性和标度不变性,分别证明它们中的每一个就会得到共形不变性。考虑到这一点,研究人员首先着手证明标度不变性,他们认为旋转不变性将是最困难的对称性。在尝试时,他们认识到他们可以证明在方形和矩形网格上的各种渗流模型的临界点存在旋转不变性。
他们使用了概率论中概率耦合(coupling)的方法,该方法可以直接比较方形晶格与旋转矩形晶格的大规模演化行为。 通过将这种方法与另一个称为可积系统领域的思想相结合,该领域研究演化系统中的隐藏结构,他们能够证明模型中相变点的行为是相同的——从而建立旋转不变性。之后他们证明了他们的结果可以扩展到其他物理模型。
最终结果证明了旋转不变性是二维模型的普遍属性。他们工作的成功表明,融合不同数学领域的类似方法对于在共形不变性方面取得进一步的研究进展是必要的。
“我认为,在共形不变性的论证和相变研究中,你需要一点点证明。你不能只从一个角度来证明它。”杜米尼尔·科平说。
自斯米尔诺夫2001年的证明以来,数学家第一次对证明共形不变性的普遍性有了新的认识。 与早期的工作不同,这个新结果开辟了新的方法。通过使用遵循自下而上的方法,他们希望一次证明一个组成部分的对称性。
现在,随着旋转不变性被证明,杜米尼尔·科平和他的同事们将目光投向了标度不变性,这是他们最初的目标。考虑到最近关于旋转对称的工作,标度不变性的证明将使数学家处于证明完全共形不变性的时刻,证明方法的灵活性使研究人员对其感到乐观。
“我认为第三步很快就会被证明,”杜米尼尔·科平说。“如果不是我们,那就是更聪明的人,但我可以肯定这很快就会发生。”然而,旋转不变性的证明耗费了五年时间,所以下一个结果可能还需要一些时间。 尽管如此,斯米尔诺夫还是希望共形不变性最终可以被证明。斯米尔诺夫说:“这可能需要一周时间,也可能需要五年,但我比11月时乐观得多。”
[1]https://arxiv.org/abs/2012.11672
[2]http://www.wisdom.weizmann.ac.il/profile/scientists/kozma-profile.html
[3]https://www.ihes.fr/en/professeur/hugo-duminil-copin-2/
[4]http://www.ens-lyon.fr/PHYSIQUE/presentation/annuaire/kozlowski-karol
[5]https://homeweb.unifr.ch/manolesc/Pub/
[6]https://www.ihes.fr/~oulamara/
[7]http://www.unige.ch/~smirnov/
[8]https://www.quantamagazine.org/the-cartoon-picture-of-magnets-that-has-transformed-science-20200624/
[9]https://phy.princeton.edu/people/alexander-polyakov
[10]http://jetpletters.ru/cgi-bin/articles/download.cgi/1737/article_26381.pdf
[11]https://arxiv.org/abs/0909.4499
[12]https://www.unige.ch/~smirnov/papers/icm-publ.pdf
[13]https://nyuad.nyu.edu/en/academics/divisions/science/faculty/federico-camia.html
原文链接:
https://www.quantamagazine.org/mathematicians-prove-symmetry-of-phase-transitions-20210708/
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

点击“阅读原文”,追踪复杂科学顶刊论文