齐夫定律(Zipf’s law)是一种典型的幂律分布,从语言中词汇的出现频率,到国家人口在不同规模城市间的分布,再到网页访问频率、收入的排序,都遵循齐夫定律。不过,齐夫定律为什么普遍存在?齐夫本人认为,这是因为系统要遵循最省力原则。2021年9月 PRL 发表的题为“最大化多样性和齐夫定律”的论文,通过求解统计模型指出,齐夫定律总是与组成部分规模的多样性最大化同时发生。而最大化多样性背后反映的,或许正是更一般的最省力原则和物理学中的最小作用量原理。
研究领域:齐夫定律,幂律分布,多样性,信息熵,最省力原则
潘佳栋、十三维 | 作者
梁金 | 审校
邓一雪 | 编辑

论文题目:
Maximal Diversity and Zipf’s Law
论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.128301
齐夫定律是哈佛大学语言学家乔治·齐夫(George Zipf)1949年发现的一个实验定律,即在自然语言里,一个单词出现的频率与它在频率表里的排序成反比。
例如,在英语的 Brown 语料库中,「the」、「of」、「and」是出现频率最高,排序 1、2、3 的单词,分别占整个语料库100万个单词数的 7%、3.6%、2.9%[1]。可见排序第2位「of」的频率大约是第1「the」的1/2,第3的「and」是其 1/3。以此类推,排序第n单词的频率是最常见频率的1/n。最简单的齐夫定律排序遵从一次反比即 1/f 关系。由此可以得到它的等价描述:
在给定语料中,对于任意一个单词,其频率(Frequency)与频率排序(Rank)乘积大致是一个常数,即:Rank * Frequency ≈ Constant
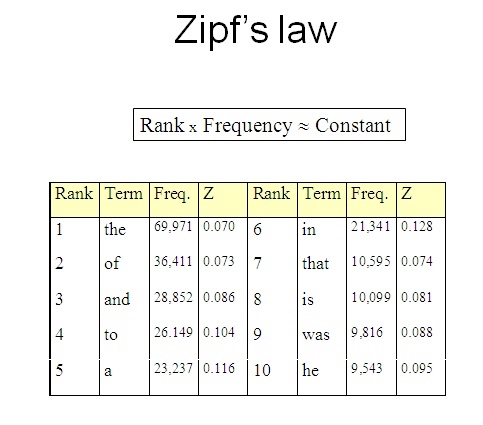
图1:齐夫定律。排序和(绝对)频率呈反比,或者说乘积为一个常数。
对数学家和统计学家来说,齐夫定律是一种典型的幂律分布,更确切说是另一种统计分布帕累托分布(Pareto distribution)的特例。后者亦称帕累托定律,最形象的描述为「二八定律」:任何国家的20%的人口拥有80%的国民财富,完成80%的工作需要20%的工作量等。这些分布都反映了一种普遍的「穷者愈穷,富者愈富」的幂律现象。在齐夫定律中,则是第1富有的是第n富有的n倍。
齐夫定律是定量语言学研究中基于经验发现的第一个数学规律,却可以在很多非语言学领域的排序中被观察到。例如不同国家中城市的数量、公司的规模、网页访问频率、收入排序、地震震级、固体破碎时的碎片大小等等。
可是齐夫定律为什么普遍存在?
齐夫在自己一部著作《最省力原则——人类行为生态学导论》中给出了一个基于人类行为和经济学的解释。他认为,人本身作为一个「能量-物质」系统,为了解决某个问题,一定会遵循所做全部功(work)最小、或成本(cost)最小的路径移动,这既包括系统本身的物质-能量流动,也包括整体单位在环境中的移动,并称之为最省力原则(Principle of Least Effort)。

例如,齐夫认为,语言作为一个交流系统,因为要遵循最省力原则,会出现两种经济:言者经济和听者经济。前者追求一招打遍天下,就像拥有一个万能装备木匠,要集成锯子、锤子等所有功能;但对听者来说,如果像婴儿或猫那样只会发一个音,就需要花费大量精力才能解码它究竟在说什么。于是语言中就出现了两种相互矛盾的经济:
(1)言者经济:词汇表仅由一个词语组成,它指称所有 m 个不同的意义。齐夫称之为「统一化之カ」(the Force of Unification);
(2) 听者经济:词汇表由 m 个词语组成,m 个词语指称 m 个意义。称之为「多元化之カ」(the Force of Diversification)。
于是在极端冲突的这两种力作用下,为遵循最省力原则,特定语言的词汇不断优化,最终决定了词语中实际数量的词汇和意义。

这种说法有道理吗?时过境迁,从过去到当代,对这个问题的探究也从经验转向了理论。今年5月 PRL 发表的一篇论文 Maximal Diversity and Zipf’s Law 中,多名研究者联合通过求解一个统计模型,定义了一个系统多样性指数 D,计算发现系统组成部分大小的多样性最大化总是与齐夫定律同时发生,并随系统总维数增加而增加。随后研究者测试了语言学和城市人口分布,发现数据与模型非常吻合。
研究者认为,在齐夫定律发生的情况下,会将多样性提升到一种驱动力的作用,这就导致了自然、社会和人文科学许多系统组成部分共同遵守的经验分布,并且很可能和自然演化优化过程高度相关。
多样性是生态学、经济学、信息论等学科的核心概念,可以通过多种多样性指标[2,3]量化,例如物种丰度、Gini-Simpson 指数或香农熵。高度多样性往往可以代表适应性和性能方面的优势。例如在生态学中,分化良好的生态系统通常被认为更稳定[4-7],同样在经济上强大的国家也往往有更多样的生产方式 [8]。但多数情况下,多样性会受到各种限制因素影响。如生态中可用的能量和物质量,就不会允许人口无限增加。同样,一个经济体所生产的不同产品的数量也受到其实力限制。因此,多样性转化(diversity drift)是一个复杂的优化过程。
在考虑诸多限制下,本研究中采用了基于丰富度指数(richness index)的多样性度量,它代表某个集合中的不同种类对象的数量,适合对复杂系统中的优化趋势进行定量描述。例如对整数集而言, {3, 7, 1, 9, 0, 1} 就比 {3, 2, 3, 7, 7, 2} 丰富,前者有五个不同的数字,后者只有三个。
研究者考虑了可以通过标签定量识别的一般情况,即对实体集合 的丰富度。对任意 N,若sn代表总资源 S 分配给第n个实体的部分,如大小,则通过累加有
的丰富度。对任意 N,若sn代表总资源 S 分配给第n个实体的部分,如大小,则通过累加有  。
。
实体可以是总人口为S的国家的城市[13],长度为S的书中以特定绝对频率出现的一个词[14],或一个由蛋白质总数S合成的细胞中以丰度{sn}表达的基因[15]等等。
齐夫定律是频率和排序呈一次反比关系。分别以s(r)和 r表示,则当 成立时,定律成立。设
成立时,定律成立。设  ,用 p(s) 分布函数来表示[17,23]即有:
,用 p(s) 分布函数来表示[17,23]即有: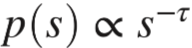 。
。
考虑N个整数的随机变量集,则可以给出一个特定位形 和相应配分函数(partition function)下,s在总大小S下的概率分布:
和相应配分函数(partition function)下,s在总大小S下的概率分布:
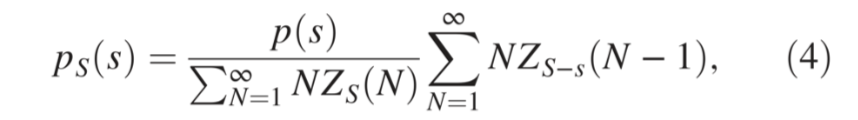
在给定位形C中,如果定义 ts 为部分大小 s∈[1,S] 出现的次数,那么多样性指数 D(diversity index D)被定义为:
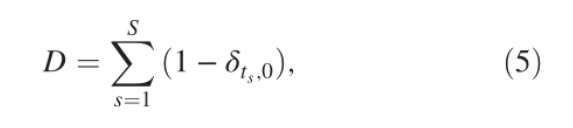
δ为克罗内克函数,对δij,当 i=j 时值1,否则为0。因此D就是被指派为不同值大小的实体或组件种类的数量,且 D ≤ N。
研究对高度多样化的位形更感兴趣,因此考虑能获得广泛大小范围的幂律分布:
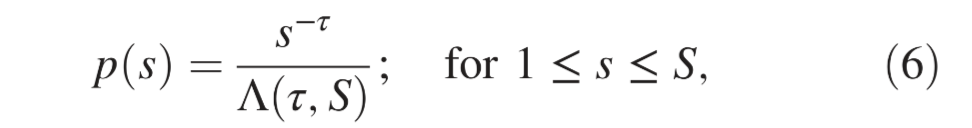
分母是一个能用黎曼 Zeta 函数表达的广义的调和数。这样我们就得到了 的精确表达。
的精确表达。
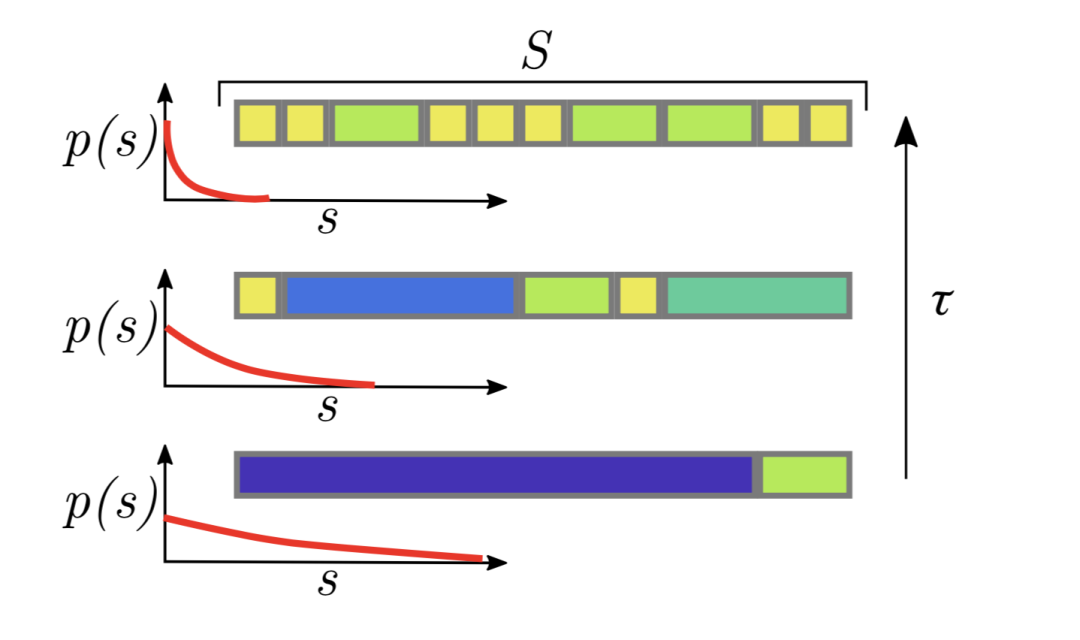
图2:组块部分大小分布 p(s) 随 s 的变化图,右边从下到上幂律 p(s) ~s-τ 随指数 τ 的增加。相同大小的实体被描述为相同色块,所有实体加起来条形总长度为S。对于较大的 τ ,大多数实体都有较小的和相似的尺寸,导致多样性较低;在另一端较小的 τ,大尺寸更容易出现(本应导致更大尺寸多样性),但因为会导致填充 S 所需的实体总数 N 变少,故多样性也比较低。在 τ 的中间值上,多样性有望达到最大。
研究目标是计算平均多样性 <D>s 和使其最大化的 τ 值。经对<D>s 拆分计算可知,其估计只取决于系统组件平均数 <N>s 和 ps(s)。二者都可以用递归方法精确求到[11],但这里只需根据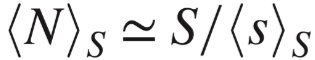 对较大 S 即可得到有效估计:
对较大 S 即可得到有效估计:
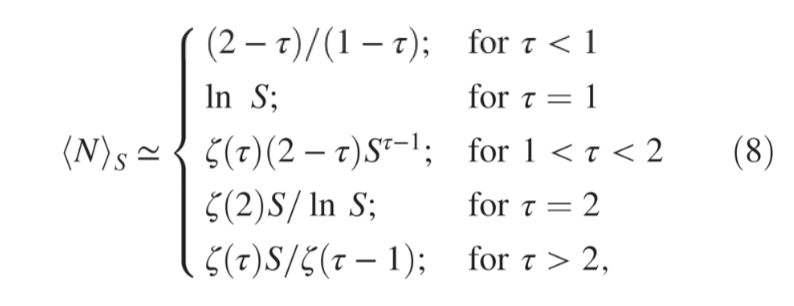
即不同的幂指数 τ 下,大小为 S 的系统组件平均数量 <N>s。这个公式可以看做是与齐夫定律相关的 Heaps 定律[37](即给定语料大小 n,独立单词数 V(n) 是 n 的指数函数)的推广,它反映了不同 S 下组件分布(本研究是ps(s))统计具有鲁棒性的系统[27,28]。
由此可以得到平均多样性 <D>s 的估计:

公式(11)被称为多样性定律。从图3可以看出对越大的S,平均多样性 <D>s 越大,但都在 τ = 2 附近达到峰值。图2则表明,这种现象是由于实体数<N>s的丰富度,与实体大小多样性之间的竞争所致,大的 τ 有利于实体数的丰度,而小的 τ 则有利于实体的多样性。
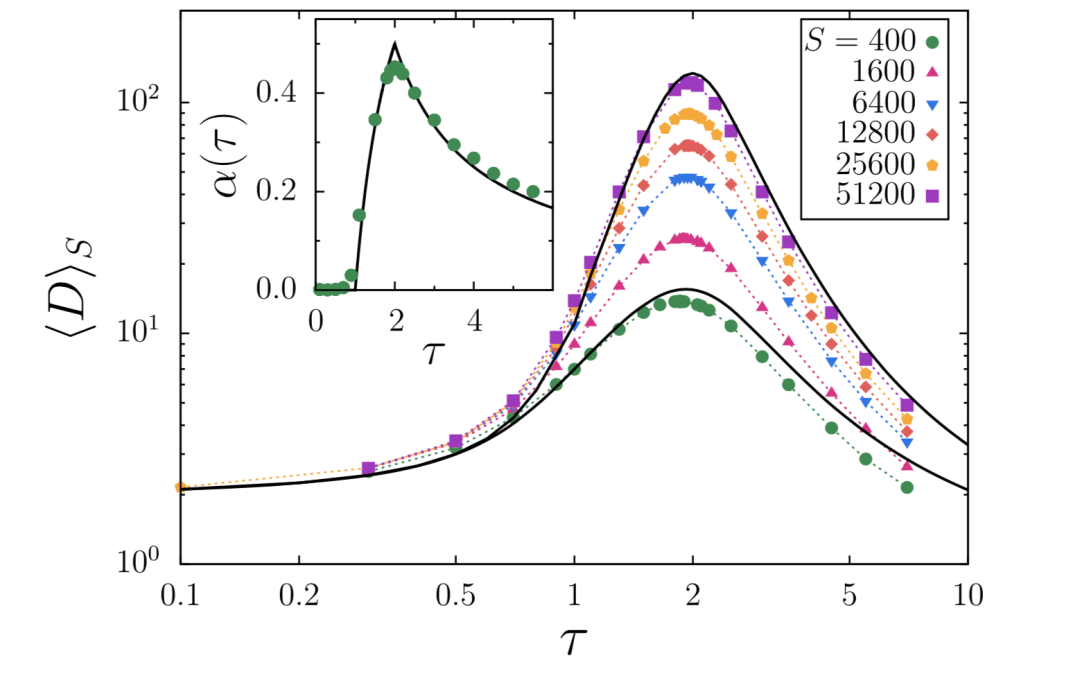
图3:以虚线表示的平均多样性 <D>s,由公式(11)对不同大小的 S 模拟得到。不同实块统计遵从全局约束位形下的分布(6),结果是104~106种位形的平均数。仅显示两端的实线是由公式(10)给出的分析解。
插图:在公式(11)下,由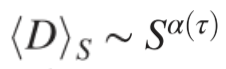 ,以 τ 为变量的指数 α(τ),实线是分析结果,圆点是模拟数据拟合。
,以 τ 为变量的指数 α(τ),实线是分析结果,圆点是模拟数据拟合。
此外研究者们还证明[11],在文献中通常考虑的几种多样性中,D是唯一一种与齐夫定律相关的最大化的度量。反之,无论什么机制,如果一个系统显示服从 τ ≃ 2 的齐夫定律,它就处于最大多样性的边缘。
有许多典型系统都遵从齐夫定律[16,17]行为,例如国家GDP[18]、公司规模[19]、物种分类[20]、分裂过程[21]等。研究人员通过两个例子验证了模型的有效性。
第一个例子是定量语言学。这是最初发现齐夫定律的领域,也几乎在所有人类语言中被观察到。
Moreno Sánchez 等人[25]曾整理了古腾堡计划一个非常庞大的英文书籍(超过30000本)数据库, 检查了齐夫定律各项参数在整个频率区间上的数据描述程度,发现与以 τ≃2 为中心的指数分布有非常好的一致性。
一本书的总大小 S 是它包含的总单词数,不同的单词数是实体的数量 N,每个实体大小 s 是其绝对频率,即这个词出现了多少次。因此,多样性指数D是一个给定文本显示的不同频率的数量。分析结果与 τ=2 的公式(11)曲线一起显示在图4中,理论预测与实验点分布相当一致,显示表明大量书籍的 τ 接近于2。
第二个例子,考虑一个国家的总人口 S 在其城市中是如何分布的。研究者使用了 GeoNames 中欧洲国家的数据[26],Simini 和 James [46]曾研究表明,城市的人口规模 s 密切遵循齐夫分布(τ≃2.02)。多样性指数D显示在图4底部。这里考虑了城市大于某个下限问题。尽管数据具有噪声,但与理论之间具有很好的一致性。

图4:上面板:单词数据集的多样性指数 D。绿点是古腾堡数据库中30000多本英文书,黑方块则是超过20个点的平均值。实线为 τ=2 下公式(11) 的曲线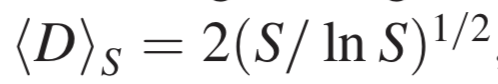 ,这对应于最大的多样性。
下面板:GeoNames 数据库中的城市的多样性指数 D。每个绿点是一个欧洲国家,黑方块是相应的平均值。实线是补充材料[11]中考虑了每个国家最小城市人口下限(sL≈1313)的曲线,虚线是
,这对应于最大的多样性。
下面板:GeoNames 数据库中的城市的多样性指数 D。每个绿点是一个欧洲国家,黑方块是相应的平均值。实线是补充材料[11]中考虑了每个国家最小城市人口下限(sL≈1313)的曲线,虚线是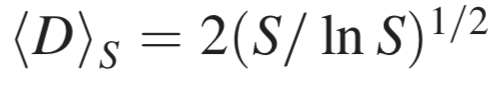 的曲线,随着国家总人口 S 不断增大,二者逐渐重合。
的曲线,随着国家总人口 S 不断增大,二者逐渐重合。
至此总结一下,这篇论文证明了,一个总大小为 S 的有限资源系统,对其 N 个组件的尺寸进行分配,最大多样性划分总会伴随齐夫定律出现,并与特定系统的具体机制无关。具体而言:
总大小为 S 的系统:
对固定 S 的系统:
即大的 τ 有利于组件种类数 <N>,小的 τ 则有利于组件尺寸的多样性 <D>,二者竞争结果,导致当 τ≈2 时,系统平均多样性<D>取得最大值。
多样性和信息是描述复杂统计系统的基本概念,多样性越高,系统的信息熵就越大[30,31],该研究表明,在遵从齐夫定律的系统中,多样性指数D发挥了重要作用。
至于为何如此,研究者们最后推想,当以适当的成本函数的极值为框架时,赋予某些问题相应的补充描述,就可能形成某种新策略,在这种情况下,多样性将扮演一个重要的驱动力角色。
这时,我们再回顾最开始齐夫本人对齐夫定律的思考会发现,最大多样性很可能就是更大的最省力原则的一部分。在齐夫之后,很多研究者从信息通讯角度进行了研究,发现通讯系统要达到最优传输就会涌现出齐夫定律行为[32][39]。此外还有一些其它研究,证明齐夫定律与最大输出效率有关。如在 arxiv 一篇预印本论文 [33]上,作者通过引入效率的概率泛函,证明生命体类似于热机,遵从齐夫定律和最省力原则就会产生最大效率输出。
为什么这些系统都会遵循最省力原则?追本溯源,其实齐夫一开始考虑的「物质-能量」系统,就来自物理学的最小作用量原理(least action principle),它可表述为哈密顿原理(Hamilton’s principle)。在根本上它们都是数学上一类讨论泛函极值问题的变分原理(Variational principle)。
图5:哈密顿原理:事物真实运动状态总是力图使哈密顿作用量(即拉格朗日函数L的积分S)取极值,通常是最小值。这条最短路径称为正路(真实运动,红色),其余路径称为旁路(可能运动)。
最小作用量原理几乎体现在一切数学和物理系统中:
并不意外,最小作用量原理其实也是幂律分布的一种成因。在数学上,幂律可由广义中心极限定理[40]给出:n个趋于无穷、具有独立同分布、方差可无限的随机变量的和会趋向 Levy稳定分布(尾端即幂律分布;方差有限则给出正态分布)。而从最小作用量原理看,其中幂律是随机变量满足条件无限方差条件下能使信息熵具有最大值的唯一分布,即在可能空间中,就像光走最短路径,随机变量整体也取得「极值」并呈现出了最优分布曲线。
此外,具有最大多样性和信息熵的系统,也不仅仅具备稳定性和鲁棒性。根据学者斯科特·佩奇(Scott E. Page)的说法,还具有所谓「多样性红利」。他证明了一个定理[34]:对于系统的需要创新和探索的难题,多样性本身会带来超出原有系统平均值的预测能力。
这种能力超过一个体——如天才的能力。显然这是一个涌现的过程。此外从算法角度看,这也是模拟自然演化的进化计算,对多目标或组合优化问题具有非常优异的效果[36-38]。
齐夫定律总与组成部分规模的多样性最大化同时发生,这种自然相关性,背后反映的是更一般的最省力原则和最小作用量原理。如果把自然看成一种通信系统和动力系统,那么要取得包括未来在内可能平均效率的最大化,不仅要在言者经济(发送端、起点)内部优化,形成统一机制(统一化之カ),还必须借助「多元化之力」在听者经济优化(接收端、表达方、终点),以最小消耗成本通往未来新的系统自身和外部可能路径。
我们知道,根据个体信息理论,生命本身是一种能将自身信息从过去传播到未来、并保持一定时间完整性度量的集合体[42]。在这个过程中,广义中心极限定理保证了幂律分布会产生最大信息熵,让最大多样性成为最小作用量原理新的起点,以最大效率「解决」某种尚未明确、未知方向的「难题」。
参差多态乃幸福的本源。就现实意义而言,多元化之力的实质是产生了多样性视角(非某种名义上的标签),通过超加性产生超过了任何单一组块的能力的「红利」,这是一个自下而上涌现的过程,对解决没有既往路径借鉴、需要创新才能解决的难题至关重要。
道法自然,本文研究让我们看到,自然不仅仅会走我们看到的最短路径。以后当我们欣赏参差多态、美丽多姿的世界时,也可以像诗人一样说,哦,原来那也是大自然在最完美高效地表达自己。
[1] Fagan, Stephen; Gençay, Ramazan (2010), “An introduction to textual econometrics”, in Ullah, Aman; Giles, David E. A. (eds.), Handbook of Empirical Economics and Finance, CRC Press, pp. 133–153, ISBN 9781420070361. P. 139: “For example, in the Brown Corpus, consisting of over one million words, half of the word volume consists of repeated uses of only 135 words.”
[2] L. Jost, Oikos 113, 363 (2006).
[3] H. Tuomisto, Oecologia 164, 853 (2010).
[4] A. R. Ives and S. R. Carpenter, Science 317, 58 (2007).
[5] C. S. Elton, The Ecology of Invasions by Animals and Plants (Methuen & Co. Ltd., London, United Kingdom, 1958).
[6] D. Tilman, P. B. Reich, and J. M. Knops, Nature (London) 441, 629 (2006).
[7] F. Arese Lucini, F. Morone, M. S. Tomassone, and H. A.Makse, PLoS One 15, e0228692 (2020).
[8] A. Tacchella, M. Cristelli, G. Caldarelli, A. Gabrielli, and L.Pietronero, Sci. Rep. 2, 723 (2012).
[9] A. Rényi et al., in Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability (The Regents of the University of California, Berkeley, 1961), Vol. 1.
[10] C. Tsallis, J. Stat. Phys. 52, 479 (1988).
[11] See Supplemental Material at http://link.aps.org/ supplemental/10.1103/PhysRevLett.127.128301 for an account of Rényi entropies, their connection with diversity indices and arguments for studying specifically the diversity index D considered in this paper based on numerical simulations, an explicit expression for the probability distribution of the diversity pSðDÞ, an exact computation of the dressed probability distribution pSðsÞ and pSðNÞ, motivations for the approximation pSðsÞ ≃ pðsÞ, the case of power law bare distributions with a lower cutoff sLblue and details of the analysis of population datasets, and an account of the behaviour of diversity in the random allocation model, which includes Ref. [12]
[12] F. Corberi, Phys. Rev. E 95, 032136 (2017).
[13] X. Gabaix, Q. J. Econ. 114, 739 (1999).
[14] S. T. Piantadosi, Psychon. Bull. Rev. 21, 1112 (2014).
[15] C. Furusawa and K. Kaneko, Phys. Rev. Lett. 90, 088102 (2003).
[16] G. K. Zipf, Human Behaviour and the Principle of Least Effort: An Introduction to Human Ecology (AddisonWesley, Cambridge, MA, 1949).
[17] M. E. J. Newman, Contemp. Phys. 46, 323 (2005).
[18] A. Clauset, C. R. Shalizi, and M. E. Newman, SIAM Rev. 51, 661 (2009).
[19] M. Cristelli, M. Batty, and L. Pietronero, Sci. Rep. 2, 812 (2012).
[20] R. L. Axtell, Science 293, 1818 (2001).
[21] J. C. Willis and G. U. Yule, Nature (London) 109, 177 (1922).
[22] L. Oddershede, P. Dimon, and J. Bohr, Phys. Rev. Lett. 71, 3107 (1993).
[23] A. Corral, I. Serra, and R. Ferrer-i-Cancho, Phys. Rev. E 102, 052113 (2020).
[34] A. de Azevedo-Lopes, A. R. de la Rocha, P. M. C. de Oliveira, and J. J. Arenzon, Phys. Rev. E 101, 012108 (2020).
[25] I. Moreno-Sánchez, F. Font-Clos, and A. Corral, PLoS One 11, e0147073 (2016).
[26] GeoNames, www.geonames.org.
[27] L. Lü, Z.-K. Zhang, and T. Zhou, PLoS One 5, e14139 (2010).
[28] G. De Marzo, A. Gabrielli, A. Zaccaria, and L. Pietronero, Phys. Rev. Research 3, 013084 (2021).
[29] L. Lü, Z.-K. Zhang, and T. Zhou, Sci. Rep. 3, 1082 (2013).
[30] M. Marsili, I. Mastromatteo, and Y. Roudi, J. Stat. Mech.(2013) P09003.
[31] R. J. Cubero, J. Jo, M. Marsili, Y. Roudi, and J. Song, J. Stat.Mech. (2019) 063402.
[32] Mandelbrot B 1954 Word 10 1-27, 424-25
[33] Principle of least effort vs. maximum efficiency: deriving Zipf-Pareto’s laws,https://arxiv.org/abs/2003.02376
[34] https://www.thegreatcourses.com/courses/the-hidden-factor-why-thinking-differently-is-your-greatest-asset
[35] 智能优化算法及其MATLAB实例(第2版)
[37] M. Joshi, M. Gyanchandani and D. Rajesh Wadhvani, “Analysis Of Genetic Algorithm, Particle Swarm Optimization and Simulated Annealing On Benchmark Functions,” 2021 5th International Conference on Computing Methodologies and Communication (ICCMC), 2021, pp. 1152-1157, doi: 10.1109/ICCMC51019.2021.9418458.
[39] Corominas-Murtra B, Fortuny J, Solé R V. Emergence of Zipf’s law in the evolution of communication[J]. Physical Review E, 2011, 83(3): 036115.
[40] B.V. Gnedenko, A.N., Kolmogorov: Limit distributions for sums of independent random variables, Addison-Wesley.1954
[41] 稳定分布与广义中心极限定理 http://swarmagents.cn.13442.m8849.cn/bs/files/jake2011616211724.pdf
[42] https://link.springer.com/article/10.1007/s12064-020-00313-7#Sec10
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

点击“阅读原文”,追踪复杂科学顶刊论文






 的丰富度。对任意 N,若sn代表总资源 S 分配给第n个实体的部分,如大小,则通过累加有
的丰富度。对任意 N,若sn代表总资源 S 分配给第n个实体的部分,如大小,则通过累加有  。
。 成立时,定律成立。设
成立时,定律成立。设  ,用 p(s) 分布函数来表示[17,23]即有:
,用 p(s) 分布函数来表示[17,23]即有: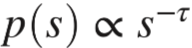 。
。 和相应配分函数(partition function)下,s在总大小S下的概率分布:
和相应配分函数(partition function)下,s在总大小S下的概率分布: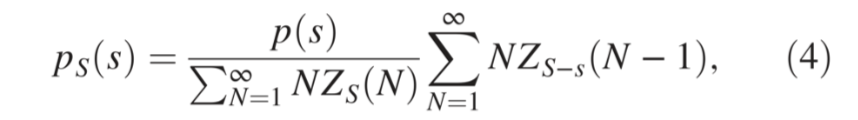
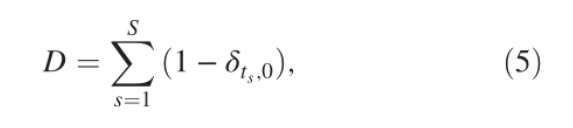
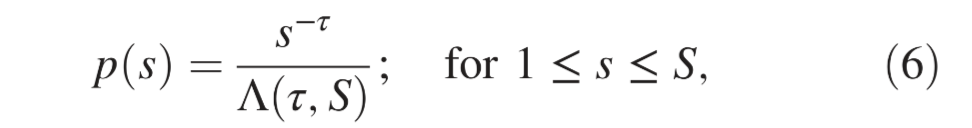
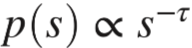 的精确表达。
的精确表达。
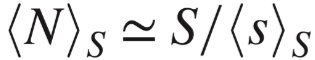 对较大 S 即可得到有效估计:
对较大 S 即可得到有效估计: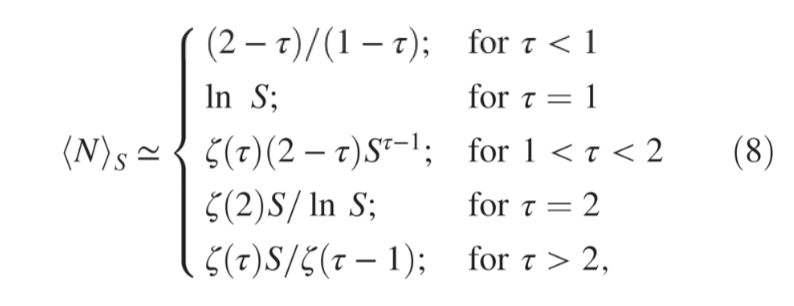


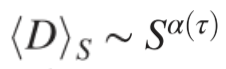 ,以 τ 为变量的指数 α(τ),实线是分析结果,圆点是模拟数据拟合。
,以 τ 为变量的指数 α(τ),实线是分析结果,圆点是模拟数据拟合。
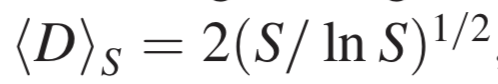 ,这对应于最大的多样性。
,这对应于最大的多样性。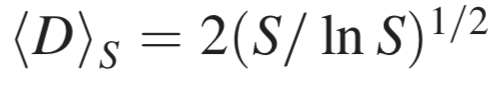 的曲线,随着国家总人口 S 不断增大,二者逐渐重合。
的曲线,随着国家总人口 S 不断增大,二者逐渐重合。