论文题目：Fermi-Bose Machine

论文地址：https://arxiv.org/abs/2404.13631

深度神经网络通过模仿人脑处理信息的方式，利用多层的非线性变换对数据进行抽象和特征提取。然而，深度神经网络在处理对抗性样本时表现出的脆弱性，即对抗性攻击，已成为该领域的一大难题。这些攻击通过在合法输入中加入不易察觉的扰动，就能导致深度神经网络做出错误的决策，这不仅对安全性构成威胁，也暴露了深度神经网络在泛化能力上的不足。

此外，深度神经网络的主流训练方法——反向传播算法，虽然训练效果显著，但其工作原理与生物神经系统的学习机制存在本质差异。反向传播算法需要全局误差信号的反向传递，这在生物神经系统中并无对应的机制，且其训练过程中的计算成本较高。这些因素激发了对新型学习算法的探索，特别是那些既能够提高模型的鲁棒性，又能够模拟生物学习过程的算法。

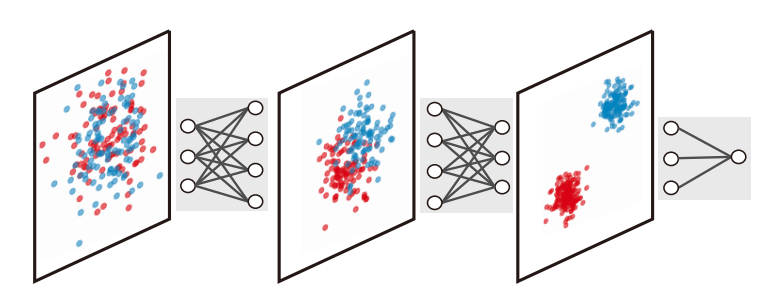
在此背景下，中山大学黄海平团队从物理学理论出发，设计出了全新的学习算法——费米-玻色机。费米-玻色机摒弃了传统的反向传播算法，转而采用局部对比学习策略，通过模拟费米子和玻色子的行为，实现了输入数据在隐藏层的语义区分。费米-玻色机采用了多层神经网络，在L层结构中，有L-2个隐藏层，用于实现数据语义层次化表示。其训练过程是局部的，每层独立学习，不需要全局误差的反向传播。

该方法所基于的基本物理思想是费米子排斥，玻色子凝聚。在量子力学和统计力学中，费米子（Fermion）和玻色子（Boson）是两类基本粒子，它们遵循不同的统计规律：1）费米子：遵循费米-狄拉克统计，具有半整数自旋，如电子、质子和中子等。费米子在空间中不能有两个或多个粒子占据同一量子态，这一性质称为泡利不相容原理，即费米子排斥现象。2）玻色子：遵循玻色-爱因斯坦统计，具有整数自旋，如光子、胶子等。多个玻色子可以占据同一量子态，即玻色子具有凝聚特点，这在激光和超导现象中起着关键作用。

在论文中，作者借鉴了费米子和玻色子的这些特性来设计深度神经网络的局部对比学习：1）玻色子对：神经网络中的同类数据对被视作玻色子对，在隐藏层表示中，这些表示倾向于彼此靠近，即距离缩小，以增强同类数据的相似性。2）费米子对：不同类数据对被视作费米子对，在隐藏层表示中，这些表示倾向于彼此远离，即距离扩大，以增强不同类数据的区分性。通过模拟这两种量子粒子的特性，费米-玻色机能够在潜在空间中实现数据的几何分离。

在统计力学框架下，作者具体分析了费米-玻色机的工作原理。本文的理论模型主要基于高斯混合数据（Gaussian mixture data），该方法假设所有数据点都是从高斯分布（正态分布）中生成，每个高斯分布都有其位置参数（均值）和形状参数（协方差），进而能够捕捉数据中的复杂结构与多样性。通过高斯混合数据，可以捕捉与分析费米-玻色机的关键特性，以及这些特性如何影响模型性能。在费米-玻色机中，目标费米对距离（target fermion-pair distance）是一个关键参数，它决定了不同类别数据点在潜在空间中应保持的最小距离。通过调整这个距离，可以控制模型对于不同类别数据点的分离程度，从而影响模型的泛化能力和对抗性鲁棒性。

该论文进一步在MNIST手写识别数据集上进行了实验验证。结果显示，相比于多层感知机模型，费米-玻色机不仅能够有效地提高模型对于对抗性攻击的鲁棒性，还能在不牺牲准确度的前提下，实现对输入数据的更优表示。特别是在调整目标费米对距离参数时，费米-玻色机的泛化准确率表现出双峰现象，揭示了表示几何与模型性能之间的深刻联系（存在一个最优的表示几何，既能提高模型泛化能力，也能增强对抗性鲁棒性）。

AI for Science与Science for AI领域正如火如荼，费米-玻色机作为物理启发机器学习的新进展，解决了深度学习技术的一些关键问题。并且，费米-玻色机可能有监督Hebbian学习（模拟生物神经系统突出可塑性的学习规则）有潜在的联系。未来，表示几何与模型鲁棒性之间的精确数学机制也有待进一步挖掘。费米-玻色机有望进一步推广到无监督学习任务中，与自编码器或生成模型等前沿工作碰撞出火花。

这个工作表明广为流传的反向传播可能是深度神经网络容易被迷惑的根本原因，而基于物理第一性原理设计的费米玻色机具有局域学习的特征，而且逐层的神经表示从几何上可控，可与大脑视觉通路对信息整合与分离的过程相佐证。

书籍推荐

黄海平教授在2021年出版了Statistical Mechanics of Neural Networks 书籍，这本书涵盖了用于理解神经网络原理的必要统计力学知识，包括复本方法、空腔方法、平均场近似、变分法、随机能量模型、Nishimori条件、动力学平均场理论、对称性破缺、随机矩阵理论等，同时详细描述了监督学习、无监督学习、联想记忆网络、感知器网络、随机循环网络等神经网络及其功能的物理模型以及解析理论。本书通过简洁的模型展示了神经网络原理的数学美和物理深度，并介绍了相关历史和展望未来研究的重要课题，可供对神经网络原理感兴趣的学生、研究人员以及工程师阅读参考。本书国外 Springer 由发行，目前可在 Amazon 平台购买。国内由高教出版社发行。

书籍相关联的解读课程

集智学园平台《神经网络的统计力学》课程，课程链接：https://campus.swarma.org/course/4543，系统讲解统计力学的基本原理及其在理解神经网络内部工作原理的应用。

统计物理方法是一座架起微观作用到宏观涌现的桥梁，2021年诺贝尔物理学奖得主帕里西在无序系统方面作出开创之举，他提出复本对称破缺方法解决自旋玻璃问题，这一方法也对神经网络等交叉学科产生深厚影响，激发未来对人工智能和人脑等复杂系统的进一步研究。本节课程是系列课程的第二节课程，介绍什么是自旋玻璃、自旋玻璃应用的几个经典例子、为什么需要空腔方法、空腔方法的基本思想和具体推导以及消息传递算法等内容，搭建从统计物理到神经网络重要的桥梁，帮助大家更好理解神经网络的基本原理。

课程详情：

黄海平：神经网络的统计力学课程 | 50人免费名额

点击“阅读原文”，报名课程